In an earlier communication to the Gazette [1], the authors in effect showed, in a somewhat complicated manner, how to evaluate the integral 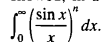 One can show in a simpler manner, however, how to evaluate, for integers n and m, a more general integral of the form
One can show in a simpler manner, however, how to evaluate, for integers n and m, a more general integral of the form 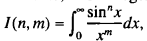 where n ≥ m, provided that if m = 1, then n is odd.
where n ≥ m, provided that if m = 1, then n is odd.
In addition, the final section to this article shows how to extend the procedure to include integrals for which m does not even have to be an integer, and also how to integrate 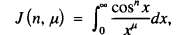 where such an integral converges.
where such an integral converges.
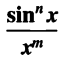 and others
and others