Article contents
The tables of John Wallis and the discovery of his product π
Published online by Cambridge University Press: 23 January 2015
Extract
In the year 1656 John Wallis published his Arithmetica Infinitorum, [1], in which he displayed many ideas that were to lead to the integral calculus of Newton. In this work we find the celebrated infinite product of Wallis which gives π,
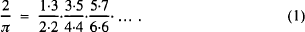
Earlier in 1593, Vieta [2] found another infinite product which gives π
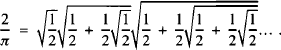
But, since Wallis does not mention it, we suppose that he was unaware of it. (Remarkably, these two seemingly different products are special cases of a more general formula [3].)
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2010
References
- 2
- Cited by


