No CrossRef data available.
Article contents
Dodecahedral slices and polyhedral pieces
Published online by Cambridge University Press: 23 January 2015
Extract
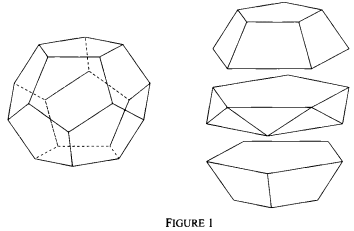
Figure 1 shows how a regular dodecahedron can be dissected into three slices by two planes through the two sets of vertices, each set defining a regular pentagon parallel to the top and bottom faces. A surprising result emerges if we calculate the ratio of the volumes of the three slices. We first prove this result directly and then show it by a dissection argument using simple polyhedral pieces of five types. These pieces can be used to build many polyhedra, including the regular dodecahedron, the regular icosahedron, the great dodecahedron, the small and great stellated dodecahedra and all the Archimedean polyhedra which have icosahedral symmetry.
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2010


