No CrossRef data available.
Article contents
A note on uniform approximation of functions having a double pole
Part of:
Algorithms - Computer Science
Numerical approximation and computational geometry
Approximations and expansions
Computational aspects and applications
Other special functions
Published online by Cambridge University Press: 01 May 2014
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We consider the classical problem of finding the best uniform approximation by polynomials of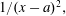 
$1/(x-a)^2,$ where 
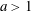$a>1$ is given, on the interval 
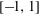$[-\! 1,1]$. First, using symbolic computation tools we derive the explicit expressions of the polynomials of best approximation of low degrees and then give a parametric solution of the problem in terms of elliptic functions. Symbolic computation is invoked then once more to derive a recurrence relation for the coefficients of the polynomials of best uniform approximation based on a Pell-type equation satisfied by the solutions.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2014
References
Achieser, N. I.,
Theory of approximation
(Dover Publications Inc., New York, 1992). Translated from the Russian and with a preface by Charles J. Hyman, reprint of the 1956 English translation.Google Scholar
Akhieser, N. I.,
Elements of the theory of elliptic functions
, Translations of Mathematical Monographs 79 (American Mathematical Society, Providence, RI, 1990). Translated from the second Russian edition by H. H. McFaden.CrossRefGoogle Scholar
Almkvist, G. and Zeilberger, D., ‘The method of differentiating under the integral sign’, J. Symbolic Comput.
10 (1990) 571–591.CrossRefGoogle Scholar
Benoit, A. and Salvy, B., ‘Chebyshev expansions for solutions of linear differential equations’,
ISSAC’09: Proceedings of the Twenty-Second International Symposium on Symbolic and Algebraic Computation
(ed. May, J.; ACM, 2009) 23–30.CrossRefGoogle Scholar
Bernstein, S. and de la Vallée Poussin, C.,
L’approximation
(Chelsea Publishing Co., Bronz, NY, 1970).Google Scholar
Bogatyrev, A.,
Extremal polynomials and Riemann surfaces
, Springer Monographs in Mathematics (Springer, Heidelberg, 2012). Translated from the 2005 Russian original by Nikolai Kruzhilin.CrossRefGoogle Scholar
Bronstein, M.,
Symbolic integration. I. Transcendental functions
, 2nd edn,
Algorithms and Computation in Mathematics 1 (Springer, Berlin, 2005), with a foreword by B. F. Caviness.Google Scholar
Buchberger, B., ‘Ein Algorithmus zum Auffinden der Basiselemente des Restklassenringes nach einem nulldimensionalen Polynomideal (An algorithm for finding the basis elements in the residue class ring modulo a zero dimensional polynomial ideal)’, PhD Thesis, Mathematical Institute, University of Innsbruck, Austria, 1965. English translation in J. Symbolic Comput., Special issue on logic, mathematics, and computer science: interactions. vol. 41, 475–511, 2006.CrossRefGoogle Scholar
Chyzak, F., ‘Fonctions holonomes en calcul formel’, Thèse universitaire, École polytechnique, 1998. INRIA, TU 0531. 227.Google Scholar
Cox, D., Little, J. and O’Shea, D., ‘An introduction to computational algebraic geometry and commutative algebra’,
Ideals, varieties, and algorithms
, 3rd edn,
Undergraduate Texts in Mathematics (Springer, New York, 2007).CrossRefGoogle Scholar
Decker, W., Greuel, G. M., Pfister, G. and Schönemann, H., Singular 3-1-3 — A computer algebra system for polynomial computations. 2011. http://www.singular.uni-kl.de.Google Scholar
Kauers, M. and Levandovskyy, V., ‘An interface between mathematica and singular’, Technical Report 2006-29, SFB F013, 2006.Google Scholar
Koutschan, C., ‘Computer algebra algorithms for
$\partial $
-finite and holonomic functions’, PhD Thesis, RISC – SFB F013, J. Kepler University, 2008.Google Scholar
$\partial $
-finite and holonomic functions’, PhD Thesis, RISC – SFB F013, J. Kepler University, 2008.Google ScholarKoutschan, C., ‘HolonomicFunctions (User’s Guide)’, Technical Report 10-01, RISC Report Series, University of Linz, Austria, January 2010.Google Scholar
Kraus, J., Pillwein, V. and Zikatanov, L., ‘Algebraic multilevel iteration methods and the best approximation to
$1/x$
in the uniform norm’, Technical report, no. 2009-17, RICAM, 2009.Google Scholar
$1/x$
in the uniform norm’, Technical report, no. 2009-17, RICAM, 2009.Google ScholarKraus, J. K., Vassilevski, P. S. and Zikatanov, L. T., ‘Polynomial of best uniform approximation to 1∕x and smoothing in two-level methods’, Comput. Methods Appl. Math.
12 (2012) 448–468.CrossRefGoogle Scholar
Privalov, I. A., ‘Approximation of 1∕x by polynomials on [−1, −a] ∪ [a, 1]’, Mat. Zametki
81 (2007) 472–473 (in Russian); translation in Math. Notes 81 (2007), 415–416.Google Scholar
Sodin, M. L. and Yuditskii, P. M., ‘Functions that deviate least from zero on closed subsets of the real axis. (in Russian)’, Algebra i Analiz
4 (1992) 1–61; translation in St. Petersburg Math. J. 4 (1993), 201–249.Google Scholar
Vlček, M. and Unbehauen, R., ‘Zolotarev polynomials and optimal FIR filters’, IEEE Trans. Signal Process.
47 (1999) 717–729.CrossRefGoogle Scholar
von zur Gathen, J. and Gerhard, J.,
Modern computer algebra
, 2nd edn (Cambridge University Press, Cambridge, 2003).Google Scholar
Whittaker, E. T. and Watson, G. N.,
A course of modern analysis. An introduction to the general theory of infinite processes and of analytic functions: with an account of the principal transcendental functions
, 4th edn (Cambridge University Press, New York, 1962).Google Scholar
You have
Access