Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T14:02:49.902Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear algebra over 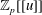$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}_p[[u]]$ and related rings

Part of: Algebraic number theory: local and $p$-adic fields Computational number theory

Published online by Cambridge University Press:  01 August 2014

Xavier Caruso  and
David Lubicz
Xavier Caruso
Affiliation:
Universté de Rennes 1, 35042 Rennes, France email [email protected]
David Lubicz
Affiliation:
Universté de Rennes 1, 35042 Rennes, France email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 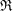$\mathfrak{R}$ be a complete discrete valuation ring, 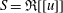$S=\mathfrak{R}[[u]]$ and 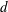$d$ a positive integer. The aim of this paper is to explain how to efficiently compute usual operations such as sum and intersection of sub-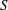$S$-modules of 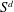$S^d$. As 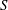$S$ is not principal, it is not possible to have a uniform bound on the number of generators of the modules resulting from these operations. We explain how to mitigate this problem, following an idea of Iwasawa, by computing an approximation of the result of these operations up to a quasi-isomorphism. In the course of the analysis of the 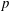$p$-adic and $u$-adic precisions of the computations, we have to introduce more general coefficient rings that may be interesting for their own sake. Being able to perform linear algebra operations modulo quasi-isomorphism with 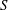$S$-modules has applications in Iwasawa theory and 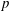$p$-adic Hodge theory. It is used in particular in Caruso and Lubicz (Preprint, 2013, arXiv:1309.4194) to compute the semi-simplified modulo 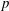$p$ of a semi-stable representation.

MSC classification

Secondary: 11Y40: Algebraic number theory computations 11S20: Galois theory
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Issue 1 , 2014 , pp. 302 - 344
Copyright
© The Author(s) 2014 

References

Caruso, X., ‘ F p -représentations semi-stables’, Ann. Inst. Fourier (Grenoble) 61 (2012) 1683–1747.Google Scholar
Caruso, X., ‘Random matrix over a dvr and lu factorization’, Preprint, 2012.Google Scholar
Caruso, X. and Lubicz, D., ‘Semi-simplifiée modulo $p$ des représentations semi-stables: une approche algorithmique’, Preprint, 2013, arXiv:1309.4194.Google Scholar
Caruso, X., Roe, D. and Vaccon, T., ‘Tracking p-adic precision’, LMS J. Comput. Math. 17 (Special issue A) (2014) 274–294.Google Scholar
Cohen, H., A course in computational algebraic number theory , Graduate Texts in Mathematics 138 (Springer, Berlin, 1993).Google Scholar
Coppersmith, D. and Winograd, S., ‘Matrix multiplication via arithmetic progressions’, J. Symbolic Comput. 9 (1990) 251–280.Google Scholar
von zur Gathen, J. and Gerhard, J., Modern computer algebra , 2nd edn (Cambridge University Press, Cambridge, 2003).Google Scholar
Hafner, J. L. and McCurley, K. S., ‘Asymptotically fast triangularization of matrices over rings’, SIAM J. Comput. 20 (1991) 1068–1083.Google Scholar
Iwasawa, K., ‘On Γ-extensions of algebraic number fields’, Bull. Amer. Math. Soc. 65 (1959) 183–226.Google Scholar
Khinchin, A. Ya., Continued fractions (The University of Chicago Press, Chicago, IL, London, 1964).Google Scholar
Lang, S., Cyclotomic fields , Graduate Texts in Mathematics 59 (Springer, New York, 1978).Google Scholar
Matsumura, H., Commutative ring theory , 2nd edn, Cambridge Studies in Advanced Mathematics 8 (Cambridge University Press, Cambridge, 1989) . Translated from the Japanese by M. Reid.Google Scholar