Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T15:02:45.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Constructing abelian surfaces for cryptography via Rosenhain invariants

Part of: Finite fields and commutative rings (number-theoretic aspects) Computational number theory Algebraic number theory: global fields Arithmetic algebraic geometry

Published online by Cambridge University Press:  01 August 2014

Craig Costello ,
Alyson Deines-Schartz ,
Kristin Lauter  and
Tonghai Yang
Craig Costello
Affiliation:
Microsoft Research, One Microsoft Way, Redmond, WA 98052, USA email [email protected]
Alyson Deines-Schartz
Affiliation:
Department of Mathematics, University of Washington, Seattle, WA 98195, USA email [email protected]
Kristin Lauter
Affiliation:
Microsoft Research, One Microsoft Way, Redmond, WA 98052, USA email [email protected]
Tonghai Yang
Affiliation:
Department of Mathematics, University of Wisconsin, Madison, WI 53706, USA email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper presents an algorithm to construct cryptographically strong genus 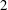$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}2$ curves and their Kummer surfaces via Rosenhain invariants and related Kummer parameters. The most common version of the complex multiplication (CM) algorithm for constructing cryptographic curves in genus 2 relies on the well-studied Igusa invariants and Mestre’s algorithm for reconstructing the curve. On the other hand, the Rosenhain invariants typically have much smaller height, so computing them requires less precision, and in addition, the Rosenhain model for the curve can be written down directly given the Rosenhain invariants. Similarly, the parameters for a Kummer surface can be expressed directly in terms of rational functions of theta constants. CM-values of these functions are algebraic numbers, and when computed to high enough precision, LLL can recognize their minimal polynomials. Motivated by fast cryptography on Kummer surfaces, we investigate a variant of the CM method for computing cryptographically strong Rosenhain models of curves (as well as their associated Kummer surfaces) and use it to generate several example curves at different security levels that are suitable for use in cryptography.

MSC classification

Secondary: 11G10: Abelian varieties of dimension $> 1$ 11R37: Class field theory 11G15: Complex multiplication and moduli of abelian varieties 11G20: Curves over finite and local fields 11T71: Algebraic coding theory; cryptography 11Y16: Algorithms; complexity
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Special Issue A: Algorithmic Number Theory Symposium XI , 2014 , pp. 157 - 180
Copyright
© The Author(s) 2014 

References

Atkin, A. O. L. and Morain, F., ‘Elliptic curves and primality proving’, Math. Comp. 61 (1993) no. 203, 29–68.Google Scholar
Bernstein, D. J., ‘A software implementation of NIST P-224’, Talk at ECC, October 2001.Google Scholar
Bernstein, D. J., ‘Elliptic vs. hyperelliptic, part I’, Talk at ECC, September 2006.Google Scholar
Bernstein, D. J., Chuengsatiansup, C., Lange, T. and Schwabe, P., ‘Kummer strikes back: new DH speed records’, http://cr.yp.to/papers.html#kummer.Google Scholar
Bernstein, D. J. and Lange, T., ‘Faster addition and doubling on elliptic curves’, Advances in cryptology – ASIACRYPT 2007, Lecture Notes in Computer Science 4833 (ed. Kurosawa, K.; Springer, 2007) 29–50.CrossRefGoogle Scholar
Bos, J. W., Costello, C., Hisil, H. and Lauter, K., ‘Fast cryptography in genus 2’, Advances in cryptology – EUROCRYPT 2013, Lecture Notes in Computer Science 7881 (eds Johansson, T. and Nguyen, P. Q.; Springer, 2013) 194–210. Full version: http://eprint.iacr.org/2012/670.CrossRefGoogle Scholar
Broker, R., Gruenewald, D. and Lauter, K., ‘Explicit CM-theory for level 2-structures on abelian surfaces’, Algebra Number Theory 5 (2011) no. 4, 495–528.CrossRefGoogle Scholar
Bruinier, J. H., Kudla, S. S. and Yang, T., ‘Special values of Green functions at big CM points’, Int. Math. Res. Not. IMRN 2012 (2012) no. 9, 1917–1967.Google Scholar
Cardona, G. and Quer, J., ‘Field of moduli and field of definition for curves of genus 2’, Computational aspects of algebraic curves, Lecture Notes Series on Computing 13 (World Scientific, Hackensack, NJ, 2005) 71–83.CrossRefGoogle Scholar
Chudnovsky, D. and Chudnovsky, G. V., ‘Sequences of numbers generated by addition in formal groups and new primality and factorization tests’, Adv. Appl. Math. 7 (1986) no. 4, 385–434.Google Scholar
Cosset, R., ‘Factorization with genus 2 curves’, Math. Comp. 79 (2010) no. 270, 1191–1208.CrossRefGoogle Scholar
Edwards, H., ‘A normal form for elliptic curves’, Bull. Amer. Math. Soc. 44 (2007) no. 3, 393–422.CrossRefGoogle Scholar
Eisentraeger, K. and Lauter, K., ‘A CRT algorithm for constructing genus 2 curves over finite fields’, Arithmetic, geometry, and coding theory (AGCT 2005), Séminaires et Congrès 21 (eds Rodier, F. and Vladut, S.; Societe Mathematique de France, 2011) 161–176.Google Scholar
Enge, A. and Thomé, E., ‘Computing class polynomials for abelian surfaces’, Experiment. Math., to appear, http://eprint.iacr.org/2013/299.Google Scholar
Gaudry, P., ‘Fast genus 2 arithmetic based on theta functions’, J. Math. Cryptology 1 (2007) no. 3, 243–265.CrossRefGoogle Scholar
Gaudry, P., Houtmann, T., Kohel, D. R., Ritzenthaler, C. and Weng, A., ‘The 2-adic CM method for genus 2 curves with application to cryptography’, Advances in cryptology – ASIACRYPT 2006, Lecture Notes in Computer Science 4284 (eds Lai, X. and Chen, K.; Springer, 2006) 114–129.CrossRefGoogle Scholar
Gaudry, P. and Schost, E., ‘Genus 2 point counting over prime fields’, J. Symbolic Comput. 47 (2012) no. 4, 368–400.CrossRefGoogle Scholar
Goren, E. Z. and Lauter, K. E., ‘Genus 2 curves with complex multiplication’, Int. Math. Res. Not. IMRN 2012 (2012) no. 5, 1068–1142.CrossRefGoogle Scholar
Gruenewald, D., ‘Computing Humbert surfaces and applications’, Arithmetic, geometry, cryptography and coding theory 2009 (American Mathematical Society, Providence, RI, 2010) 59–69.CrossRefGoogle Scholar
Igusa, J., ‘On Siegel modular forms of genus two’, Amer. J. Math. (1962) 175–200.Google Scholar
Lauter, K. and Viray, B., ‘An arithmetic intersection formula for denominators of Igusa class polynomials’, Preprint, 2012, arXiv:1210.7841.Google Scholar
Lenstra, A. K., Lenstra, H. W. and Lovász, L., ‘Factoring polynomials with rational coefficients’, Math. Ann. 261 (1982) no. 4, 515–534.Google Scholar
Lubicz, D. and Robert, D., ‘A generalisation of Miller’s algorithm and applications to pairing computations on abelian varieties’, Cryptology ePrint Archive, Report 2013/192, 2013, http://eprint.iacr.org/.Google Scholar
Mestre, J., ‘Construction de courbes de genre 2 à partir de leurs modules’, Effective methods in algebraic geometry, Progress in Mathematics 94 (Birkhäuser, Boston, MA, 1991) 313–334.Google Scholar
Milne, J. S., ‘Class field theory (v4.02)’, 2013, available at www.jmilne.org/math/.Google Scholar
Montgomery, P. L., ‘Speeding the Pollard and elliptic curve methods of factorization’, Math. Comp. 48 (1987) no. 177, 243–264.Google Scholar
Pila, J., ‘Frobenius maps of abelian varieties and finding roots of unity in finite fields’, Math. Comp. 55 (1990) no. 192, 745–763.Google Scholar
Schoof, R., ‘Elliptic curves over finite fields and the computation of square roots mod p’, Math. Comp. 44 (1985) no. 170, 483–494.Google Scholar
Shimura, G., Introduction to the arithmetic theory of automorphic functions, vol. 1 (Princeton University Press, Princeton, NJ, 1971).Google Scholar
Shimura, G., Abelian varieties with complex multiplication and modular functions, vol. 46 (Princeton University Press, Princeton, NJ, 1998).CrossRefGoogle Scholar
Spallek, A., ‘Kurven vom Geschlecht 2 und ihre Anwendung in public-key-Kryptosystemen’, PhD Thesis, Inst. für Experimentelle Mathematik, 1994.Google Scholar
Streng, M., ‘Complex multiplication of abelian surfaces’, PhD Thesis, Leiden University, June 2010,https://openaccess.leidenuniv.nl/handle/1887/15572.Google Scholar
Streng, M., ‘An explicit version of Shimura’s reciprocity law for Siegel modular functions’, CoRR, 2012, arXiv:abs/1201.0020.Google Scholar
van Wamelen, P., ‘Equations for the Jacobian of a hyperelliptic curve’, Trans. Amer. Math. Soc. 350 (1998) no. 8, 3083–3106.CrossRefGoogle Scholar
van Wamelen, P., ‘Examples of genus two CM curves defined over the rationals’, Math. Comp. 68 (1999) no. 225, 307–320.CrossRefGoogle Scholar
Weng, A., ‘Constructing hyperelliptic curves of genus 2 suitable for cryptography’, Math. Comp. 72 (2003) no. 241, 435–458.CrossRefGoogle Scholar
Yang, T., ‘Arithmetic intersection on a Hilbert modular surface and the Faltings height’, Asian J. Math. 17 (2013) no. 2, 335–382.CrossRefGoogle Scholar
Yang, T., ‘Rational structure of $X(N)$ over $\mathbb{Q}$ and explicit Galois action on CM points’, Preprint, 2014.Google Scholar