Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T00:37:42.407Z Has data issue: false hasContentIssue false
  • English
  • Français

Computing fundamental domains for the Bruhat–Tits tree for 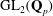${\rm GL}_2(\mathbf{Q}_p)$, 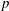$p$-adic automorphic forms, and the canonical embedding of Shimura curves

Part of: Other groups of matrices Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  01 April 2014

Cameron Franc  and
Marc Masdeu
Cameron Franc
Affiliation:
Department of Mathematics, University of California Santa Cruz, Santa Cruz, CA 95064, USA email [email protected]
Marc Masdeu
Affiliation:
Department of Mathematics, Columbia University, New York, NY 10027, USA email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We describe algorithms that allow the computation of fundamental domains in the Bruhat–Tits tree for the action of discrete groups arising from quaternion algebras. These algorithms are used to compute spaces of rigid modular forms of arbitrary even weight, and we explain how to evaluate such forms to high precision using overconvergent methods. Finally, these algorithms are applied to the calculation of conjectural equations for the canonical embedding of p-adically uniformizable rational Shimura curves. We conclude with an example in the case of a genus 4 Shimura curve.

MSC classification

Secondary: 11F06: Structure of modular groups and generalizations; arithmetic groups 20H10: Fuchsian groups and their generalizations
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Issue 1 , 2014 , pp. 1 - 23
Copyright
© The Author(s) 2014 

References

Baker, M., Savitt, D. and Thakur, D. S., p-adic geometry: lectures from the 2007 Arizona winter school University Lecture Series vol. 45, (American Mathematical Society, Providence, RI, 2008).Google Scholar
Böckle, G. and Butenuth, R., ‘On computing quaternion quotient graphs for function fields’, J. Théor. Nombres Bordeaux 24 (2012) 73–99.CrossRefGoogle Scholar
Boutot, J.-F. and Carayol, H., ‘Uniformisation $p$ -adique des courbes de Shimura: les théorèmes de Čerednik et de Drinfel’d’, Astérisque 196–197 (1991) 45–158; Courbes modulaires et courbes de Shimura (Orsay, 1987/1988).Google Scholar
Clark, P. L., ‘Rational points on Atkin–Lehner quotients of shimura curves’, PhD Thesis, Harvard University, Cambridge, MA, 2003.Google Scholar
Cohen, H., A course in computational algebraic number theory Graduate Texts in Mathematics 138, (Springer, 1993).Google Scholar
Darmon, H., Rational points on modular elliptic curves , CBMS Regional Conference Series in Mathematics 101 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Darmon, H. and Pollack, R., ‘Efficient calculation of Stark–Heegner points via overconvergent modular symbols’, Israel J. Math. 153 (2006) 319–354.CrossRefGoogle Scholar
Dasgupta, S. and Teitelbaum, J., The p-adic upper half plane, p-adic geometry , University Lecture Series 45 (American Mathematical Society, Providence, RI, 2008) 65–121.Google Scholar
Gerritzen, L. and van der Put, M., Schottky groups and Mumford curves , Lecture Notes in Mathematics 817 (Springer, Berlin, 1980).Google Scholar
Greenberg, M., ‘Heegner point computations via numerical p-adic integration’, Algorithmic Number Theory (2006) 361–376.Google Scholar
Greenberg, M., ‘Heegner points and rigid analytic modular forms’, PhD Thesis, McGill University, 2006.Google Scholar
Hartshorne, R., Algebraic geometry (Springer, 1977).Google Scholar
Kirschmer, M. and Voight, J., ‘Algorithmic enumeration of ideal classes for quaternion orders’, SIAM J. Comput. 39 (2010) 1714–1747.Google Scholar
Kontogeorgis, A. and Rotger, V., ‘On the non-existence of exceptional automorphisms on Shimura curves’, Bull. Lond. Math. Soc. 40 (2008) 363–374.CrossRefGoogle Scholar
Kurihara, A., ‘On $p$ -adic Poincaré series and Shimura curves’, Internat. J. Math. 5 (1994) 747–763.CrossRefGoogle Scholar
Lubotzky, A., Discrete groups, expanding graphs and invariant measures , Modern Birkhäuser Classics (Birkhäuser, Basel, 2010 reprint of the 1994 edition).Google Scholar
Molina, S., ‘Equations of hyperelliptic Shimura curves’, Proc. Lond. Math. Soc. (3) 105 (2012) 891–920.Google Scholar
Ogg, A. P., ‘Real points on Shimura curves’, Arithmetic and geometry, vol. I , Progress in Mathematics 35 (Birkhäuser, Boston, MA, 1983) 277–307.Google Scholar
Pollack, R. and Stevens, G., ‘Overconvergent modular symbols and $p$ -adic $L$ -functions’, Ann. Sci. Éc. Norm. Supér. (4) 44 (2011) 1–42.Google Scholar
Serre, J.-P., Letter to Tate, Oct. 24, 1984.Google Scholar
Serre, J.-P., ‘Trees’, Springer Monographs in Mathematics (Springer, Berlin, 2003).Google Scholar
Sijsling, J., ‘Equations for arithmetic pointed Tori’, PhD Thesis, Utrecht University, Utrecht, Netherlands, 2010.Google Scholar
Stein, W. A. et al. , Sage Mathematics Software (Version 4.7.2), The Sage Development Team, 2011, http://www.sagemath.org.Google Scholar
Stevens, G., ‘Rigid analytic modular symbols’, Preprint, 1994.Google Scholar
Teitelbaum, J. T., ‘Values of $p$ -adic $L$ -functions and a $p$ -adic Poisson kernel’, Invent. Math. 101 (1990) 395–410.Google Scholar
Vignéras, M.-F., Arithmétique des algèbres de quaternions , Lecture Notes in Mathematics 800 (Springer, Berlin, 1980).Google Scholar