Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-04T21:08:55.618Z Has data issue: false hasContentIssue false
  • English
  • Français

Computing boundary extensions of conformal maps

Part of: Geometric function theory Computability and recursion theory Miscellaneous topics of analysis in the complex domain Proof theory and constructive mathematics Fairly general properties

Published online by Cambridge University Press:  01 September 2014

Timothy H. McNicholl
Timothy H. McNicholl*
Affiliation:
Department of Mathematics, Iowa State University, Ames, IA 50011, USA email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that a computable and conformal map of the unit disk onto a bounded domain 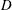$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}D$ has a computable boundary extension if 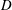$D$ has a computable boundary connectivity function.

MSC classification

Secondary: 03D78: Computation over the reals 30C30: Numerical methods in conformal mapping theory 30E10: Approximation in the complex domain 03F60: Constructive and recursive analysis 54D05: Connected and locally connected spaces (general aspects)
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Issue 1 , 2014 , pp. 360 - 378
Copyright
© The Author 2014 

References

Beurling, A., ‘Ensembles exceptionnels’, Acta Math. 72 (1940) 1–13.CrossRefGoogle Scholar
Binder, I., Braverman, M. and Yampolsky, M., ‘On the computational complexity of the Riemann mapping’, Arch. Mat. 45 (2007) 221–239.Google Scholar
Bishop, E. and Bridges, D., Constructive analysis , Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] 279 (Springer, Berlin, 1985).CrossRefGoogle Scholar
Brattka, V., ‘Plottable real number functions and the computable graph theorem’, SIAM J. Comput. 38 (2008) no. 1, 303–328.CrossRefGoogle Scholar
Brattka, V. and Weihrauch, K., ‘Computability on subsets of Euclidean space. I. Closed and compact subsets’, Theoret. Comput. Sci. 219 (1999) no. 1–2, 65–93; Computability and complexity in analysis (Castle Dagstuhl, 1997).CrossRefGoogle Scholar
Braverman, M. and Cook, S., ‘Computing over the reals: foundations for scientific computing’, Notices Amer. Math. Soc. 53 (2006) no. 3, 318–329.Google Scholar
Cheng, H., ‘A constructive Riemann mapping theorem’, Pacific J. Math. 44 (1973) 435–454.CrossRefGoogle Scholar
Cooper, S. B., Computability theory (Chapman & Hall/CRC, Boca Raton, FL, 2004).Google Scholar
Couch, P. J., Daniel, B. D. and McNicholl, T. H., ‘Computing space-filling curves’, Theory Comput. Syst. 50 (2012) no. 2, 370–386.CrossRefGoogle Scholar
Daniel, D. and McNicholl, T. H., ‘Effective local connectivity properties’, Theory Comput. Syst. 50 (2012) no. 4, 621–640.CrossRefGoogle Scholar
Garnett, J. B. and Marshall, D. E., Harmonic measure , New Mathematical Monographs 2 (Cambridge University Press, Cambridge, 2005).CrossRefGoogle Scholar
Greene, R. and Krantz, S., Function theory of one complex variable , Graduate Studies in Mathematics (American Mathematical Society, Providence, RI, 2002).Google Scholar
Grzegorczyk, A., ‘On the definitions of computable real continuous functions’, Fund. Math. 44 (1957) 61–71.CrossRefGoogle Scholar
Hertling, P., ‘An effective Riemann mapping theorem’, Theoret. Comput. Sci. 219 (1999) 225–265.CrossRefGoogle Scholar
Hocking, J. G. and Young, G. S., Topology , 2nd edn (Dover, New York, 1988).Google Scholar
Koebe, P., ‘Über eine neue Methode der Konformen Abbildung und Uniformisierung’, Nachr. Kgl. Ges. Wiss. Göttingen Math.-Phys. Kl. 1912 (1912) 844–848.Google Scholar
Lacombe, D., ‘Extension de la notion de fonction récursive aux fonctions d’une ou plusieurs variables réelles. I’, C. R. Acad. Sci. Paris 240 (1955) 2478–2480.Google Scholar
Lacombe, D., ‘Extension de la notion de fonction récursive aux fonctions d’une ou plusieurs variables réelles. II, III’, C. R. Acad. Sci. Paris 241 (1955) 13–14; 151–153.Google Scholar
Marshall, D. E. and Rohde, S., ‘Convergence of a variant of the zipper algorithm for conformal mapping’, SIAM J. Numer. Anal. 45 (2007) 2577–2609.CrossRefGoogle Scholar
McNicholl, T. H., ‘An effective Carathéodory theorem’, Theory Comput. Syst. 50 (2012) no. 4, 579–588.CrossRefGoogle Scholar
McNicholl, T. H., ‘Computing links and accessing arcs’, Math. Logic Quart. 59 (2013) no. 1–2, 101–107.CrossRefGoogle Scholar
McNicholl, T. H., ‘The power of backtracking and the confinement of length’, Proc. Amer. Math. Soc. 141 (2013) no. 3, 1041–1053.CrossRefGoogle Scholar
McNicholl, T. H., ‘Computing boundary extensions of conformal maps part 2’, Preprint, 2013, arXiv:1304.1915, submitted.Google Scholar
Odifreddi, P. G., Classical recursion theory. The theory of functions and sets of natural numbers , 1st edn (North-Holland, Amsterdam, 1989).Google Scholar
Pommerenke, Ch., Boundary behaviour of conformal maps , Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] 299 (Springer, Berlin, 1992).CrossRefGoogle Scholar
Pour-El, M. B. and Richards, J. I., Computability in analysis and physics , Perspectives in Mathematical Logic (Springer, Berlin, 1989).CrossRefGoogle Scholar
Rudin, W., Real and complex analysis , 3rd edn (McGraw-Hill, New York, 1987).Google Scholar
Specker, E., ‘Nicht konstruktiv beweisbare Sätze der Analysis’, J. Symbolic Logic 14 (1949) 145–158.CrossRefGoogle Scholar
Turing, A. M., ‘On computable numbers, with an application to the Entscheidungsproblem. A correction’, Proc. Lond. Math. Soc. Series 2 (1937) no. 43, 544–546.Google Scholar
Weihrauch, K., Computable analysis , Texts in Theoretical Computer Science. An EATCS Series (Springer, Berlin, 2000).CrossRefGoogle Scholar