Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T13:10:53.652Z Has data issue: false hasContentIssue false
  • English
  • Français

A classification of all 1-Salem graphs

Part of: Algebraic number theory: global fields Graph theory

Published online by Cambridge University Press:  01 November 2014

Lee Gumbrell  and
James McKee
Lee Gumbrell
Affiliation:
Department of Mathematics, Royal Holloway, University of London, Egham Hill, Egham, Surrey, TW20 0EX, United Kingdom email [email protected]
James McKee
Affiliation:
Department of Mathematics, Royal Holloway, University of London, Egham Hill, Egham, Surrey, TW20 0EX, United Kingdom email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

One way to study certain classes of polynomials is by considering examples that are attached to combinatorial objects. Any graph 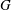$G$ has an associated reciprocal polynomial 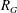$R_{G}$, and with two particular classes of reciprocal polynomials in mind one can ask the questions: (a) when is 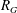$R_{G}$ a product of cyclotomic polynomials (giving the cyclotomic graphs)? (b) when does 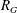$R_{G}$ have the minimal polynomial of a Salem number as its only non-cyclotomic factor (the non-trivial Salem graphs)? Cyclotomic graphs were classified by Smith (Combinatorial structures and their applications, Proceedings of Calgary International Conference, Calgary, AB, 1969 (eds R. Guy, H. Hanani, H. Saver and J. Schönheim; Gordon and Breach, New York, 1970) 403–406); the maximal connected ones are known as Smith graphs. Salem graphs are ‘spectrally close’ to being cyclotomic, in that nearly all their eigenvalues are in the critical interval 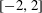$[-2,2]$. On the other hand, Salem graphs do not need to be ‘combinatorially close’ to being cyclotomic: the largest cyclotomic induced subgraph might be comparatively tiny.

We define an 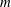$m$-Salem graph to be a connected Salem graph 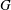$G$ for which 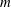$m$ is minimal such that there exists an induced cyclotomic subgraph of 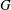$G$ that has 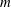$m$ fewer vertices than 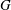$G$. The 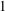$1$-Salem subgraphs are both spectrally close and combinatorially close to being cyclotomic. Moreover, every Salem graph contains a 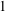$1$-Salem graph as an induced subgraph, so these 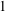$1$-Salem graphs provide some necessary substructure of all Salem graphs. The main result of this paper is a complete combinatorial description of all 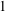$1$-Salem graphs: in the non-bipartite case there are 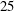$25$ infinite families and 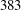$383$ sporadic examples.

MSC classification

Primary: 11R06: PV-numbers and generalizations; other special algebraic numbers; Mahler measure 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.)
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Issue 1 , 2014 , pp. 582 - 594
Copyright
© The Author(s) 2014 

References

Boyd, D. W., ‘Small Salem numbers’, Duke Math. J. 44 (1977) no. 2, 315–328.Google Scholar
Cameron, P. J., Goethals, J. M., Seidel, J. J. and Shult, E. E., ‘Line graphs, root systems, and elliptic geometry’, J. Algebra 43 (1976) 305–327.CrossRefGoogle Scholar
Cameron, P. J. and van Lint, J. H., Designs, graphs, codes and their links (Cambridge University Press, Cambridge, 1991).CrossRefGoogle Scholar
Cannon, J. W. and Wagreich, Ph., ‘Growth functions of surface groups’, Math. Ann. 293 (1992) 239–257.Google Scholar
Cauchy, A. L., ‘Sur l’équation à l’aide de laquelle on détermine les inégalitiés séculaires des mouvements des planètes’, Oeuvres complètes, Iièeme Série 9 (Gauthier-Villars, 1829) 174–195.Google Scholar
Cvetković, D., Doob, M. and Gutman, I., ‘On graphs whose eigenvalues do not exceed √2 +√ 5’, Ars Combin. 14 (1982) 225–239.Google Scholar
Cvetković, D., Rowlinson, P. and Simić, S., Spectral generalizations of line graphs: on graphs with least eigenvalue − 2 , London Mathematical Society Lecture Note Series 314 (Cambridge University Press, Cambridge, 2004).Google Scholar
Dobrowolski, E., ‘A note on integer symmetric matrices and Mahler’s measure’, Canad. Math. Bull. 51 (2008) no. 1, 57–59.Google Scholar
Estes, D. R., ‘Eigenvalues of symmetric integer matrices’, J. Number Theory 42 (1992) 292–296.Google Scholar
Godsil, C. and Royle, G., Algebraic graph theory (Springer, New York, 2001).Google Scholar
Gumbrell, L., ‘On spectral constructions for Salem graphs’, PhD Thesis, 2013.Google Scholar
Hoffman, A. J., ‘On limit points of spectral radii of non-negative symmetric matrices’, Graph theory and its applications , Lecture Notes in Mathematics 303 (Springer, Berlin, 1972) 165–172.Google Scholar
Hoffman, A. J., ‘Eigenvalues of graphs’, Studies in graph theory (ed. Fulkerson, D. R.; Mathematical Association of America, Washington, DC, 1975) 225–245.Google Scholar
Kronecker, L., ‘Zwei sätse über gleichungen mit ganzzahligen coefficienten’, J. Reine Angew. Math. 53 (1857) 173–175.Google Scholar
Lakatos, P., ‘On spectral radius of Coxeter transformation of trees’, Publ. Math. Debrecen 54 (1999) 181–187.Google Scholar
Lakatos, P., ‘Salem numbers, PV numbers and spectral radii of Coxeter transformations’, C. R. Math. Acad. Sci. Soc. R. Can. 23 (2001) 71–77.Google Scholar
Lakatos, P., ‘Salem numbers defined by Coxeter transformation’, Linear Algebra Appl. 432 (2010) 144–154.Google Scholar
McKee, J., ‘Families of Pisot numbers with negative trace’, Acta Arith. 93 (2000) no. 4, 373–385.CrossRefGoogle Scholar
McKee, J., ‘Small-span characteristic polynomials of integer symmetric matrices’, Algorithmic number theory (9th International Symposium, ANTS-IX, Nancy, France) , Springer Lecture Notes in Computer Science 6197 (eds Hanrot, G., Morain, F. and Thomé, E.; Springer, 2010) 270–284.Google Scholar
McKee, J. and Smyth, C., ‘Salem numbers of trace − 2, and traces of totally positive algebraic integers’, Algorithmic number theory (6th International Symposium, ANTS-VI, Burlington, USA) , Springer Lecture Notes in Computer Science 3076 (ed. Buell, D. A.; Springer, 2004) 327–337.Google Scholar
McKee, J. and Smyth, C., ‘Salem numbers, Pisot numbers, Mahler measure, and graphs’, Exp. Math. 14 (2005) 211–229.CrossRefGoogle Scholar
McKee, J. and Smyth, C., ‘Integer symmetric matrices of small spectral radius and small Mahler measure’, Int. Math. Res. Not. IMRN 2012 (2012) no. 1, 102–136, doi:10.1093/imrn/rnr011.Google Scholar
McKee, J., Smyth, C. and Rowlinson, P., ‘Salem numbers and Pisot numbers from stars’, Number Theory in Progress 1 (Zakopane-Kocielisko, 1997) (eds Győry, K., Iwaniec, H. and Urbanowicz, J.; de Gruyter, Berlin, 1999) 309–319.Google Scholar
McMullen, C. T., ‘Coxeter groups, Salem numbers and the Hilbert metric’, Publ. Math. Inst. Hautes Études Sci. 95 (2002) 151–183.Google Scholar
Parry, W., ‘Growth series of Coxeter groups and Salem numbers’, J. Algebra 154 (1993) 406–415.Google Scholar
Radosavljević, Z. and Simić, S., ‘Which bicyclic graphs are reflexive’, Univ. Beograd Publ. Elektrotehn. Fak. Ser. Mat. 14 (2003) 64–85.Google Scholar
Rašajski, M., Radosavljević, Z. and Mihailović, B., ‘Maximal reflexive cacti with four cycles: the approach via Smith graphs’, Linear Algebra Appl. 435 (2011) 2530–2543.Google Scholar
Robinson, R. M., ‘Intervals containing infinitely many sets of conjugate algebraic integers’, Mathematical analysis and related topics: essays in honor of George Pólya (Stanford, 1962) 305–315.Google Scholar
Schur, I., ‘Über die Verteilung der Wurzeln bei gewissen algebraischen Gleichungen mit ganzzahligen Koeffizienten’, Math. Z. 1 (1918) 377–402.Google Scholar
Smith, J. H., ‘Some properties of the spectrum of a graph’, Combinatorial structures and their applications, Proceedings of Calgary International Conference, Calgary, AB, 1969 (eds Guy, R., Hanani, H., Saver, H. and Schönheim, J.; Gordon and Breach, New York, 1970) 403–406.Google Scholar
Stekolshchik, R., Notes on Coxeter transformations and the McKay correspondence (Springer, Berlin, Heidelberg, 2008).Google Scholar
Zhang, Y., ‘Eigenvalues of Coxeter transformations and the structure of regular components of an Auslander–Reiten quiver’, Comm. Algebra 17 (1989) no. 10, 2347–2362.Google Scholar