Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T12:26:45.686Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximations for the Bessel and Airy functions with an explicit error term

Part of: Approximations and expansions

Published online by Cambridge University Press:  01 May 2014

Ilia Krasikov
Ilia Krasikov*
Affiliation:
Department of Mathematical Sciences, Brunel University, Uxbridge UB8 3PH, United Kingdom email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

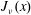We show how one can obtain an asymptotic expression for some special functions with a very explicit error term starting from appropriate upper bounds. We will work out the details for the Bessel function $J_\nu (x)$ and the Airy function 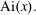${\rm Ai}(x).$ In particular, we answer a question raised by Olenko and find a sharp bound on the difference between 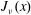$J_\nu (x)$ and its standard asymptotics. We also give a very simple and surprisingly precise approximation for the zeros 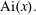${\rm Ai}(x).$

MSC classification

Secondary: 41A60: Asymptotic approximations, asymptotic expansions (steepest descent, etc.) 33C10: Bessel and Airy functions, cylinder functions, $_0F_1$
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Issue 1 , 2014 , pp. 209 - 225
Copyright
© The Author 2014 

References

Breen, S., ‘Uniform upper and lower bounds on the zeros of Bessel functions of the first kind’, J. Math. Anal. Appl. 196 (1995) 1–17.Google Scholar
Fabbri, I. M., Lucianetti, A. and Krasikov, I., ‘On a Sturm Liouville periodic boundary values problem’, Integral Transforms Spec. Funct. 20 (2009) 353–364.Google Scholar
Gatteschi, L. and Giordano, C., ‘Error bounds for McMahon’s asymptotic approximations of the zeros of the Bessel functions’, Integral Transforms Spec. Funct. 10 (2000) 41–56.Google Scholar
Krasikov, I., ‘Uniform bound for Bessel function’, J. Appl. Anal. 12 (2006) 83–92.Google Scholar
Krasikov, I., ‘An upper bound on Jacobi Polynomials’, J. Approx. Theory 149 (2007) 116–130.Google Scholar
Krasikov, I., ‘On Erdélyi–Magnus–Nevai conjecture for Jacobi polynomials’, Constr. Approx. 28 (2008) 113–125.Google Scholar
Krasikov, I. and Zarkh, A., ‘Equioscillatory properties of the Laguerre polynomials’, J. Approx. Theory 162 (2010) 2021–2047.Google Scholar
Olenko, A. Ya., ‘Upper bound on √x J ν (x) and its applications’, Integral Transforms Spec. Funct. 17 (2006) 455–467.Google Scholar
Olver, F. W. J., Lozier, D. W., Boisvert, R. F. and Clark, C. W. (eds), NIST Handbook of Mathematical Functions (Cambridge University Press, 2010).Google Scholar
Paris, R. B., ‘An inequality for the Bessel function J ν (ν x)’, SIAM J. Math. Anal. 15 (1984) 203–205.Google Scholar
Patrick, M. L., ‘Some inequalities concerning Jacobi Polynomials’, SIAM J. Math. Anal. 2 (1971) 213–220.Google Scholar
Patrick, M. L., ‘Extensions of inequalities of the Laguerre and Turán type’, Pacific J. Math. 44 (1973) 675–682.CrossRefGoogle Scholar
Pittaluga, G. and Sacripante, L., ‘Inequalities for the zeros of the Airy functions’, SIAM J. Math. Anal. 22 (1991) 260–267.Google Scholar
Szegö, G., Orthogonal polynomials , Colloqium Publications 23 (American Mathematical Society, Providence, RI, 1975).Google Scholar
Watson, G. N., A Treatise on the theory of Bessel function (Cambridge University Press, London, 1944).Google Scholar