A fundamental problem for the realization of laser fusion through the implosion of a spherical target is Kidder's E−1/6 law, where E is the energy needed for ignition, proportional to the 6th power of the ratio R/R0, where R0 and R are the initial and final implosion radii, respectively. This law implies that the ignition energy is very sensitive to the ratio R0/R, or vice versa, the ratio R0/R is very insensitive to the energy input, with R0/R limited by the Rayleigh–Taylor instability. According to still classified data of the Centurion–Halite experiment at the Nevada Test Site, ignition would require an energy of 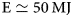${\rm E}\simeq 50\,{\rm MJ}$, 25 times larger than the 2 MJ laser at the National Ignition Facility (NIF) reported in the New York Times. This means that even a tenfold increase from 2 to 20 MJ would only decrease the R/R0 ratio by an insignificant factor of 10−1/6 ≃ 0.7. To overcome this problem, it is proposed that the spherical target is replaced with a hollowed-out, rapidly rotating, cm-size ferromagnetic target, accelerated by a rotating traveling magnetic wave to a rotational velocity of ~1 km/s, at the limit of its tensile strength. In a rotating reference system, the general theory of relativity predicts the occurrence of negative gravitational field masses in the center of rotation, with their source located in the Coriolis force field. The density of this negative gravitational field mass can be larger than the magnitude of the positive mass density of a neutron star. The repulsive gravitational force causes the centrifugal force. For a magnetized plasma placed in the rapidly spinning, hollowed-out target chamber, this repulsive force can be balanced by the magnetic force generated by thermomagnetic currents of the Nernst effect. Such a configuration does not suffer from the Rayleigh–Taylor instability, but becomes a small magnetohydrodynamic generator, amplifying the magnetic field to values about equal to those of the Nernst effect, axially confining the plasma. By placing the spinning target in the center of a lithium vortex, the fusion neutrons absorbed in the vortex can breed tritium, and at the same time remove heat from the target chamber to sustain the Nernst effect. A hot spot is thereby produced in the target chamber, which launches a thermonuclear burn wave into a cylindrical deuterium–tritium configuration. With the stability of a rapidly rotating target greatly increased, and the range of 10 MeV electrons in the wall of the cm-size ferromagnetic target, an intense 10 MeV relativistic electron beam drawn from a 10 MJ Marx generator should be sufficient to implode the target for thermonuclear ignition.