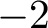1. Introduction
Asymptotic behaviour as well as estimates of heat kernels have been intensively studied in the last decades. The first results obtained by Pòlya [Reference Pólya44] and Blumenthal and Getoor [Reference Blumenthal and Getoor4] for isotropic
![]() $\alpha $
-stable process in
$\alpha $
-stable process in
![]() $\mathbb {R}^d$
provided the basis for studies of more complicated processes; for example, subordinated Brownian motions [Reference Mimica40, Reference Song49], isotropic unimodal Lévy processes [Reference Bogdan, Grzywny and Ryznar6, Reference Cygan, Grzywny and Trojan15, Reference Grzywny, Ryznar and Trojan21] and even more general symmetric Markov processes [Reference Chen, Kim and Kumagai11, Reference Chen and Kumagai14]. One may, among others, list the articles on heat kernel estimates for jump processes of finite range [Reference Chen, Kim and Kumagai10] or with lower intensity of higher jumps [Reference Mimica39, Reference Sztonyk51]. While a great many articles with explicit results are devoted to symmetric processes or those which are, in appropriate sense, similar to the symmetric ones, the nonsymmetric case is in general harder to handle due to lack of a familiar structure. This problem was approached in many different ways; see, for example, [Reference Bogdan, Sztonyk and Knopova7, Reference Ishikawa27, Reference Ishikawa28, Reference Kaleta and Sztonyk31, Reference Kaleta and Sztonyk32, Reference Knopova35, Reference Knopova and Kulik36, Reference Picard42, Reference Picard43, Reference Sztonyk50]. For a more specific class of stable processes, see [Reference Hiraba25, Reference Pruitt and Taylor46, Reference Watanabe53]. Overall, one has to impose some control on the nonsymmetry in order to obtain estimates in an easy-to-handle form. This idea was applied in the recent paper [Reference Grzywny and Szczypkowski22] where the authors considered the case of the Lévy measure being comparable to some unimodal Lévy measure. The methods developed in [Reference Grzywny and Szczypkowski22, Reference Grzywny and Szczypkowski23] contributed significantly to this article. See also [Reference Kaleta and Sztonyk32, Reference Picard42] and the references therein.
$\mathbb {R}^d$
provided the basis for studies of more complicated processes; for example, subordinated Brownian motions [Reference Mimica40, Reference Song49], isotropic unimodal Lévy processes [Reference Bogdan, Grzywny and Ryznar6, Reference Cygan, Grzywny and Trojan15, Reference Grzywny, Ryznar and Trojan21] and even more general symmetric Markov processes [Reference Chen, Kim and Kumagai11, Reference Chen and Kumagai14]. One may, among others, list the articles on heat kernel estimates for jump processes of finite range [Reference Chen, Kim and Kumagai10] or with lower intensity of higher jumps [Reference Mimica39, Reference Sztonyk51]. While a great many articles with explicit results are devoted to symmetric processes or those which are, in appropriate sense, similar to the symmetric ones, the nonsymmetric case is in general harder to handle due to lack of a familiar structure. This problem was approached in many different ways; see, for example, [Reference Bogdan, Sztonyk and Knopova7, Reference Ishikawa27, Reference Ishikawa28, Reference Kaleta and Sztonyk31, Reference Kaleta and Sztonyk32, Reference Knopova35, Reference Knopova and Kulik36, Reference Picard42, Reference Picard43, Reference Sztonyk50]. For a more specific class of stable processes, see [Reference Hiraba25, Reference Pruitt and Taylor46, Reference Watanabe53]. Overall, one has to impose some control on the nonsymmetry in order to obtain estimates in an easy-to-handle form. This idea was applied in the recent paper [Reference Grzywny and Szczypkowski22] where the authors considered the case of the Lévy measure being comparable to some unimodal Lévy measure. The methods developed in [Reference Grzywny and Szczypkowski22, Reference Grzywny and Szczypkowski23] contributed significantly to this article. See also [Reference Kaleta and Sztonyk32, Reference Picard42] and the references therein.
In this article the central object is a subordinator; that is, a one-dimensional Lévy process with nondecreasing paths starting at
![]() $0$
; see Section 2 for the precise definition. The abstract introduction of the subordination dates back to 1950s and is due to Bochner [Reference Bochner5] and Philips [Reference Phillips41]. In the language of the semigroup theory, for a Bernstein function
$0$
; see Section 2 for the precise definition. The abstract introduction of the subordination dates back to 1950s and is due to Bochner [Reference Bochner5] and Philips [Reference Phillips41]. In the language of the semigroup theory, for a Bernstein function
![]() $\phi $
and a bounded
$\phi $
and a bounded
![]() $C_0$
-semigroup
$C_0$
-semigroup
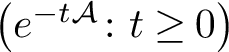 $\big ( e^{-t\mathcal {A}} \colon t \geq 0\big )$
with
$\big ( e^{-t\mathcal {A}} \colon t \geq 0\big )$
with
![]() $-\mathcal {A}$
being its generator on some Banach space
$-\mathcal {A}$
being its generator on some Banach space
![]() $\mathscr {X}$
, via Bochner integral one can define an operator
$\mathscr {X}$
, via Bochner integral one can define an operator
![]() $\mathcal {B}=\phi (\mathcal {A})$
such that
$\mathcal {B}=\phi (\mathcal {A})$
such that
![]() $-\mathcal {B}$
also generates a bounded
$-\mathcal {B}$
also generates a bounded
![]() $C_0$
-semigroup
$C_0$
-semigroup
 $\big ( e^{-t\mathcal {B}} \colon t \geq 0\big )$
on
$\big ( e^{-t\mathcal {B}} \colon t \geq 0\big )$
on
![]() $\mathscr {X}$
. The semigroup
$\mathscr {X}$
. The semigroup
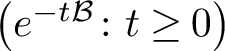 $\big ( e^{-t\mathcal {B}} \colon t \geq 0\big )$
is then said to be subordinated to
$\big ( e^{-t\mathcal {B}} \colon t \geq 0\big )$
is then said to be subordinated to
 $\big ( e^{-t\mathcal {A}} \colon t \geq 0\big )$
, and although it may be very different from the original one, its properties clearly follow from properties of both the parent semigroup and the involved Bernstein function. See, for example, [Reference Gomilko and Tomilov18] and the references therein. From a probabilistic point of view, due to positivity and monotonicity, subordinators naturally appear as random time change functions of Lévy processes or, more generally, Markov processes. Namely, if
$\big ( e^{-t\mathcal {A}} \colon t \geq 0\big )$
, and although it may be very different from the original one, its properties clearly follow from properties of both the parent semigroup and the involved Bernstein function. See, for example, [Reference Gomilko and Tomilov18] and the references therein. From a probabilistic point of view, due to positivity and monotonicity, subordinators naturally appear as random time change functions of Lévy processes or, more generally, Markov processes. Namely, if
![]() $(X_t \colon t \geq 0)$
is a Markov process and
$(X_t \colon t \geq 0)$
is a Markov process and
![]() $(T_t \colon t \geq 0)$
is an independent subordinator, then
$(T_t \colon t \geq 0)$
is an independent subordinator, then
![]() $Y_t=X_{T_t}$
is again a Markov process with a transition function given by
$Y_t=X_{T_t}$
is again a Markov process with a transition function given by
 $$ \begin{align*} \mathbb{P}^x(Y_t \in A) = \int_{[0, \infty)} \mathbb{P}^x(X_s \in A) \:\mathbb{P}(T_t \in {\textrm{d}}s). \end{align*} $$
$$ \begin{align*} \mathbb{P}^x(Y_t \in A) = \int_{[0, \infty)} \mathbb{P}^x(X_s \in A) \:\mathbb{P}(T_t \in {\textrm{d}}s). \end{align*} $$
The procedure just described is called a subordination of a Markov process and can be interpreted as a probabilistic form of the equality
![]() $\mathcal {B}=\phi (\mathcal {A})$
. Here
$\mathcal {B}=\phi (\mathcal {A})$
. Here
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
are (minus) generators of semigroups associated to processes
$\mathcal {B}$
are (minus) generators of semigroups associated to processes
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
, respectively. From an analytical point of view, the transition density of
$Y_t$
, respectively. From an analytical point of view, the transition density of
![]() $Y_t$
(the integral kernel of
$Y_t$
(the integral kernel of
![]() $e^{-t\mathcal {B}}$
) can be obtained as a time average of transition density of
$e^{-t\mathcal {B}}$
) can be obtained as a time average of transition density of
![]() $X_t$
with respect to distribution of
$X_t$
with respect to distribution of
![]() $T_t$
. Yet another approach is driven by partial differential equations, as the transition density is a heat kernel of a generalised heat equation. The generalisation can be twofold: either by replacing the Laplace operator with another, possibly nonlocal operator or by introducing a more general fractional-time derivative instead of the classical one. The latter case was recently considered in [Reference Chen9, Reference Chen, Kim, Kumagai and Wang12, Reference Meerschaert and Scheffler38]. Here the solutions are expressed in terms of corresponding (inverse) subordinators and thus their analysis is essential.
$T_t$
. Yet another approach is driven by partial differential equations, as the transition density is a heat kernel of a generalised heat equation. The generalisation can be twofold: either by replacing the Laplace operator with another, possibly nonlocal operator or by introducing a more general fractional-time derivative instead of the classical one. The latter case was recently considered in [Reference Chen9, Reference Chen, Kim, Kumagai and Wang12, Reference Meerschaert and Scheffler38]. Here the solutions are expressed in terms of corresponding (inverse) subordinators and thus their analysis is essential.
By taking
![]() $\mathcal {A}=-\Delta $
and changing the time of (i.e., subordinating) Brownian motion one can obtain a large class of subordinated Brownian motions. A principal example here is an
$\mathcal {A}=-\Delta $
and changing the time of (i.e., subordinating) Brownian motion one can obtain a large class of subordinated Brownian motions. A principal example here is an
![]() $\alpha $
-stable subordinator with the Laplace exponent
$\alpha $
-stable subordinator with the Laplace exponent
![]() $\phi (\lambda )=\lambda ^{\alpha }$
,
$\phi (\lambda )=\lambda ^{\alpha }$
,
![]() $\alpha \in (0,1)$
, which gives rise to the symmetric, rotation-invariant
$\alpha \in (0,1)$
, which gives rise to the symmetric, rotation-invariant
![]() $\alpha $
-stable process and corresponds to the special case of fractional powers of semigroup
$\alpha $
-stable process and corresponds to the special case of fractional powers of semigroup
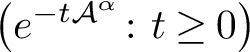 $\big (e^{-t\mathcal {A}^{\alpha }} \colon t \geq 0\big )$
. For this reason, distributional properties of subordinators were often studied with reference to heat kernel estimates of subordinated Brownian motions (see, e.g., [Reference Fahrenwaldt16, Reference Kim and Mimica33]). In [Reference Hawkes24] Hawkes investigated the growth of sample paths of a stable subordinator and obtained the asymptotic behaviour of its distribution function. Jain and Pruitt [Reference Jain and Pruitt30] considered tail probability estimates for subordinators and, in the discrete case, nondecreasing random walks. In a more general setting some related results were obtained in [Reference Fristedt and Pruitt17, Reference Iksanov, Kabluchko, Marynych and Shevchenko26, Reference Picard42, Reference Vasudeva and Divanji52]. In [Reference Burridge, Kuznetsov, Kwaśnicki and Kyprianou8] new examples of families of subordinators with explicit transition densities were given. Finally, in the recent paper [Reference Fahrenwaldt16], the author derived explicit approximate expressions for the transition density of approximately stable subordinators under very restrictive assumptions.
$\big (e^{-t\mathcal {A}^{\alpha }} \colon t \geq 0\big )$
. For this reason, distributional properties of subordinators were often studied with reference to heat kernel estimates of subordinated Brownian motions (see, e.g., [Reference Fahrenwaldt16, Reference Kim and Mimica33]). In [Reference Hawkes24] Hawkes investigated the growth of sample paths of a stable subordinator and obtained the asymptotic behaviour of its distribution function. Jain and Pruitt [Reference Jain and Pruitt30] considered tail probability estimates for subordinators and, in the discrete case, nondecreasing random walks. In a more general setting some related results were obtained in [Reference Fristedt and Pruitt17, Reference Iksanov, Kabluchko, Marynych and Shevchenko26, Reference Picard42, Reference Vasudeva and Divanji52]. In [Reference Burridge, Kuznetsov, Kwaśnicki and Kyprianou8] new examples of families of subordinators with explicit transition densities were given. Finally, in the recent paper [Reference Fahrenwaldt16], the author derived explicit approximate expressions for the transition density of approximately stable subordinators under very restrictive assumptions.
The result of the article is asymptotic behaviour as well as upper and lower estimates of transition densities of subordinators satisfying scaling condition imposed on the second derivative of the Laplace exponent
![]() $\phi $
. Our standing assumption on
$\phi $
. Our standing assumption on
![]() $-\phi ^{\prime \prime }$
is the weak lower scaling condition at infinity with scaling parameter
$-\phi ^{\prime \prime }$
is the weak lower scaling condition at infinity with scaling parameter
![]() $\alpha -2$
, for some
$\alpha -2$
, for some
![]() $\alpha>0$
(see (2.7) for definition). It is worth highlighting that we do not state our assumptions and results in terms of the Laplace exponent
$\alpha>0$
(see (2.7) for definition). It is worth highlighting that we do not state our assumptions and results in terms of the Laplace exponent
![]() $\phi $
, as one could suspect, but in terms of its second derivative and related function
$\phi $
, as one could suspect, but in terms of its second derivative and related function
![]() $\varphi (x)=x^2(-\phi ^{\prime \prime }(x))$
(see Theorems 3.3, 4.7 and 4.8). Usually the transition density of a Lévy process is described by the generalised inverse of the real part of the characteristic exponent
$\varphi (x)=x^2(-\phi ^{\prime \prime }(x))$
(see Theorems 3.3, 4.7 and 4.8). Usually the transition density of a Lévy process is described by the generalised inverse of the real part of the characteristic exponent
![]() $\psi ^{-1}(x)$
(e.g., [Reference Grzywny and Szczypkowski23], [Reference Knopova and Kulik36]), but in our setting one can show that the lower scaling property implies that
$\psi ^{-1}(x)$
(e.g., [Reference Grzywny and Szczypkowski23], [Reference Knopova and Kulik36]), but in our setting one can show that the lower scaling property implies that
![]() $\varphi ^{-1}(x) \approx \psi ^{-1}(x)$
for x sufficient large (see Proposition 4.3). In some cases, however,
$\varphi ^{-1}(x) \approx \psi ^{-1}(x)$
for x sufficient large (see Proposition 4.3). In some cases, however,
![]() $\varphi $
may be significantly different from the Laplace exponent
$\varphi $
may be significantly different from the Laplace exponent
![]() $\phi $
. However, if one assumes additional upper scaling condition with scaling parameter
$\phi $
. However, if one assumes additional upper scaling condition with scaling parameter
![]() $\beta -2$
for
$\beta -2$
for
![]() $\beta $
strictly between
$\beta $
strictly between
![]() $0$
and
$0$
and
![]() $1$
, then these two objects are comparable (see Proposition 4.6).
$1$
, then these two objects are comparable (see Proposition 4.6).
The main results of this article are covered by Theorems 3.3, 4.7, 4.8, 4.11 and 4.17. Theorem 3.3 is essential for the whole article because it provides not only the existence of the transition density but also its asymptotic behaviour, which is later used in derivation of upper and lower estimates. The key argument in the proof is the lower estimate on the holomorphic extension of the Laplace exponent
![]() $\phi $
(see Lemma 3.1), which justifies the inversion of the Laplace transform and allows us to perform the saddle point type approximation. In Theorem 3.3 we only use the weak lower scaling property on the second derivative of the Laplace exponent. In particular, we do not assume the absolute continuity of
$\phi $
(see Lemma 3.1), which justifies the inversion of the Laplace transform and allows us to perform the saddle point type approximation. In Theorem 3.3 we only use the weak lower scaling property on the second derivative of the Laplace exponent. In particular, we do not assume the absolute continuity of
![]() $\nu ({\textrm {d}} x)$
. Furthermore, the asymptotic is valid in some region described in terms of both space and time variables. By freezing one of them, we obtain as corollaries the results similar to [Reference Fahrenwaldt16]; see, for example, Corollary 3.6. It is also worth highlighting that we obtain a version of the upper estimate on the transition density with no additional assumptions on the Lévy measure
$\nu ({\textrm {d}} x)$
. Furthermore, the asymptotic is valid in some region described in terms of both space and time variables. By freezing one of them, we obtain as corollaries the results similar to [Reference Fahrenwaldt16]; see, for example, Corollary 3.6. It is also worth highlighting that we obtain a version of the upper estimate on the transition density with no additional assumptions on the Lévy measure
![]() $\nu ({\textrm {d}} x)$
; see Theorem 4.7. Clearly, putting some restrictions on
$\nu ({\textrm {d}} x)$
; see Theorem 4.7. Clearly, putting some restrictions on
![]() $\nu ({\textrm {d}} x)$
results in sharper estimates (Theorem 4.8), but it is interesting that the scaling property alone is enough to get some information. Our starting point and the main object to work with is the Laplace exponent
$\nu ({\textrm {d}} x)$
results in sharper estimates (Theorem 4.8), but it is interesting that the scaling property alone is enough to get some information. Our starting point and the main object to work with is the Laplace exponent
![]() $\phi $
. However, in many cases the primary object is the Lévy measure
$\phi $
. However, in many cases the primary object is the Lévy measure
![]() $\nu ({\textrm {d}}x)$
and results are presented in terms of or require its tail decay. Therefore, it would be convenient to have a connection between those two objects. In Proposition 3.8 we prove that one can impose scaling conditions on the tail of the Lévy measure
$\nu ({\textrm {d}}x)$
and results are presented in terms of or require its tail decay. Therefore, it would be convenient to have a connection between those two objects. In Proposition 3.8 we prove that one can impose scaling conditions on the tail of the Lévy measure
![]() $\nu ((x,\infty ))$
instead, as they imply the scaling condition on
$\nu ((x,\infty ))$
instead, as they imply the scaling condition on
![]() $-\phi ^{\prime \prime }$
.
$-\phi ^{\prime \prime }$
.
We also note that the main results of the article hold true when
![]() $-\phi ^{\prime \prime }$
is a function regularly varying at infinity with regularity index
$-\phi ^{\prime \prime }$
is a function regularly varying at infinity with regularity index
![]() $\alpha -2$
, where
$\alpha -2$
, where
![]() $\alpha>0$
. This follows easily by Potter bounds for regularly varying functions (see [Reference Bingham, Goldie and Teugels3, Theorem 1.5.6]), which immediately imply both lower and upper scaling properties. Moreover, if additionally
$\alpha>0$
. This follows easily by Potter bounds for regularly varying functions (see [Reference Bingham, Goldie and Teugels3, Theorem 1.5.6]), which immediately imply both lower and upper scaling properties. Moreover, if additionally
![]() $\alpha <1$
, then, by Karamata’s theorem and monotone density theorem, regular variation of
$\alpha <1$
, then, by Karamata’s theorem and monotone density theorem, regular variation of
![]() $-\phi ^{\prime \prime }$
with index
$-\phi ^{\prime \prime }$
with index
![]() $\alpha -2$
is equivalent to regular variation of
$\alpha -2$
is equivalent to regular variation of
![]() $\phi $
with index
$\phi $
with index
![]() $\alpha $
. This is not the case for the case
$\alpha $
. This is not the case for the case
![]() $\alpha =1$
where, in general, only the first direction holds true.
$\alpha =1$
where, in general, only the first direction holds true.
Below we present the special case when global upper and lower scaling conditions are imposed with
![]() $0 < \alpha \leq \beta < 1$
; see Theorem 4.17.
$0 < \alpha \leq \beta < 1$
; see Theorem 4.17.
Theorem A. Let
![]() $\mathbf {T}$
be a subordinator with the Laplace exponent
$\mathbf {T}$
be a subordinator with the Laplace exponent
![]() $\phi $
. Suppose that for some
$\phi $
. Suppose that for some
![]() $0 < \alpha \leq \beta < 1$
, the functions
$0 < \alpha \leq \beta < 1$
, the functions
are almost increasing and almost decreasing, respectively. We also assume that the Lévy measure
![]() $\nu ({\mathrm{d}}x)$
has an almost monotone density
$\nu ({\mathrm{d}}x)$
has an almost monotone density
![]() $\nu (x)$
. Then the probability distribution of
$\nu (x)$
. Then the probability distribution of
![]() $T_t$
has a density
$T_t$
has a density
![]() $p(t, \:\cdot \:)$
. Moreover, for all
$p(t, \:\cdot \:)$
. Moreover, for all
![]() $t \in (0, \infty )$
and
$t \in (0, \infty )$
and
![]() $x> 0$
,
$x> 0$
,
 $$ \begin{align*} p(t,x) \approx \begin{cases} \big(t \big( -\phi^{\prime\prime}(w) \big)\big)^{-1/2} \exp \left\lbrace -t \big( \phi(w) - w\phi'(w) \big) \right\rbrace, &\text{if } 0 < x\phi^{-1}(1/t) \leq 1, \\ tx^{-1}\phi(1/x), &\text{if } 1 < x\phi^{-1}(1/t), \end{cases} \end{align*} $$
$$ \begin{align*} p(t,x) \approx \begin{cases} \big(t \big( -\phi^{\prime\prime}(w) \big)\big)^{-1/2} \exp \left\lbrace -t \big( \phi(w) - w\phi'(w) \big) \right\rbrace, &\text{if } 0 < x\phi^{-1}(1/t) \leq 1, \\ tx^{-1}\phi(1/x), &\text{if } 1 < x\phi^{-1}(1/t), \end{cases} \end{align*} $$
where
![]() $w=(\phi ')^{-1}(x/t)$
.
$w=(\phi ')^{-1}(x/t)$
.
We note that a similar result to Theorem A appeared in [Reference Chen, Kim, Kumagai and Wang13] in around the same time as our preprint. Our assumptions, however, are weaker, as we assume almost monotonicity of the Lévy density instead of monotonicity of the function
![]() $t \mapsto t\nu (t)$
. Moreover, our estimates are genuinely sharp; that is, the constants appearing in the exponential factors are the same on both sides of the estimate, while estimates obtained in [Reference Chen, Kim, Kumagai and Wang13] are qualitatively sharp; that is, the constants in the exponential factors are different.
$t \mapsto t\nu (t)$
. Moreover, our estimates are genuinely sharp; that is, the constants appearing in the exponential factors are the same on both sides of the estimate, while estimates obtained in [Reference Chen, Kim, Kumagai and Wang13] are qualitatively sharp; that is, the constants in the exponential factors are different.
As a corollary, under the assumption of Theorem A, we obtain a global two-sided estimate on the Green function. Namely, for all
![]() $x>0$
,
$x>0$
,
 $$ \begin{align*} G(x) \approx \frac{1}{x\phi(1/x)}. \end{align*} $$
$$ \begin{align*} G(x) \approx \frac{1}{x\phi(1/x)}. \end{align*} $$
See Section 5 and Theorem 5.8 for details.
The article is organised as follows: In Section 2 we introduce our framework and collect some facts concerning Bernstein functions and their scaling properties. Section 3 is devoted to the proof of Theorem 3.3 and its consequences. In Section 4 we provide both upper and lower estimates on the transition density and discuss when these estimates coincide. Some applications of our results to subordination beyond the familiar
![]() $\mathbb {R}^d$
setting and Green function estimates are presented in Section 5.
$\mathbb {R}^d$
setting and Green function estimates are presented in Section 5.
Notation
By
![]() $C_1, c_1, C_2, c_2, \ldots $
we denote positive constants which may change from line to line. For two functions
$C_1, c_1, C_2, c_2, \ldots $
we denote positive constants which may change from line to line. For two functions
![]() $f,g \colon (0,\infty ) \rightarrow [0,\infty )$
we write
$f,g \colon (0,\infty ) \rightarrow [0,\infty )$
we write
![]() $f(x) \gtrsim g(x)$
if there is
$f(x) \gtrsim g(x)$
if there is
![]() $c>0$
such that
$c>0$
such that
![]() $f(x) \geq cg(x)$
for all
$f(x) \geq cg(x)$
for all
![]() $x>0$
. An analogous rule is applied to the symbol
$x>0$
. An analogous rule is applied to the symbol
![]() $\lesssim $
. We also have
$\lesssim $
. We also have
![]() $f(x) \approx g(x)$
if there exists
$f(x) \approx g(x)$
if there exists
![]() $C \geq 1$
such that
$C \geq 1$
such that
![]() $C^{-1} f(x) \leq g(x) \leq C f(x)$
for all
$C^{-1} f(x) \leq g(x) \leq C f(x)$
for all
![]() $x> 0$
. Finally, we set
$x> 0$
. Finally, we set
![]() $a \wedge b=\min \{ a,b \}$
and
$a \wedge b=\min \{ a,b \}$
and
![]() $a \vee b = \max \{a,b\}$
.
$a \vee b = \max \{a,b\}$
.
2. Preliminaries
Let
![]() $(\Omega , \mathcal {F}, \mathbb {P})$
be a probability space. Let
$(\Omega , \mathcal {F}, \mathbb {P})$
be a probability space. Let
![]() $\mathbf {T} = (T_t \colon t \geq 0)$
be a subordinator; that is, a Lévy process in
$\mathbf {T} = (T_t \colon t \geq 0)$
be a subordinator; that is, a Lévy process in
![]() $\mathbb {R}$
with nondecreasing paths. Recall that a Lévy process is a càdlàg stochastic process with stationary and independent increments such that
$\mathbb {R}$
with nondecreasing paths. Recall that a Lévy process is a càdlàg stochastic process with stationary and independent increments such that
![]() $T_0 = 0$
almost surely. There is a function
$T_0 = 0$
almost surely. There is a function
![]() $\psi \colon \mathbb {R} \rightarrow \mathbb {C}$
, called the Lévy–Khintchine exponent of
$\psi \colon \mathbb {R} \rightarrow \mathbb {C}$
, called the Lévy–Khintchine exponent of
![]() $\mathbf {T}$
, such that for all
$\mathbf {T}$
, such that for all
![]() $t \geq 0$
and
$t \geq 0$
and
![]() $\xi \in \mathbb {R}$
,
$\xi \in \mathbb {R}$
,
 $$ \begin{align*} \mathbb{E} \big( e^{i \xi T_t} \big) = e^{-t\psi(\xi)}. \end{align*} $$
$$ \begin{align*} \mathbb{E} \big( e^{i \xi T_t} \big) = e^{-t\psi(\xi)}. \end{align*} $$
Moreover, there are
![]() $b \geq 0$
and
$b \geq 0$
and
![]() $\sigma $
-finite measure
$\sigma $
-finite measure
![]() $\nu $
on
$\nu $
on
![]() $(0, \infty )$
satisfying
$(0, \infty )$
satisfying
 $$ \begin{align} \int_{(0, \infty)} \min{\{1, s\}} \: \nu({\textrm{d}}s) < \infty, \end{align} $$
$$ \begin{align} \int_{(0, \infty)} \min{\{1, s\}} \: \nu({\textrm{d}}s) < \infty, \end{align} $$
such that for all
![]() $\xi \in \mathbb {R}$
,
$\xi \in \mathbb {R}$
,

which is valid thanks to (2.1). By
![]() $\phi \colon [0, \infty ) \rightarrow [0, \infty )$
we denote the Laplace exponent of
$\phi \colon [0, \infty ) \rightarrow [0, \infty )$
we denote the Laplace exponent of
![]() $\mathbf {T}$
, namely,
$\mathbf {T}$
, namely,
 $$ \begin{align*} \mathbb{E}\big(e^{-\lambda T_t} \big) = e^{-t \phi(\lambda)} \end{align*} $$
$$ \begin{align*} \mathbb{E}\big(e^{-\lambda T_t} \big) = e^{-t \phi(\lambda)} \end{align*} $$
for all
![]() $t \geq 0$
and
$t \geq 0$
and
![]() $\lambda \geq 0$
. Let
$\lambda \geq 0$
. Let
![]() $\psi ^*$
be the symmetric continuous and nondecreasing majorant of
$\psi ^*$
be the symmetric continuous and nondecreasing majorant of
![]() $\Re \psi $
; that is,
$\Re \psi $
; that is,
 $$ \begin{align*} \psi^*(r) = \mathop{\mathrm{sup}}\limits_{|z| \leq r} \Re \psi(z), \quad r>0. \end{align*} $$
$$ \begin{align*} \psi^*(r) = \mathop{\mathrm{sup}}\limits_{|z| \leq r} \Re \psi(z), \quad r>0. \end{align*} $$
Notice that
 $$ \begin{align*} \psi^* \big( \psi^{-1}(s) \big)=s, \qquad\text{and}\qquad \psi^{-1} \big( \psi^*(s) \big) \geq s, \end{align*} $$
$$ \begin{align*} \psi^* \big( \psi^{-1}(s) \big)=s, \qquad\text{and}\qquad \psi^{-1} \big( \psi^*(s) \big) \geq s, \end{align*} $$
where
![]() $\psi ^{-1}$
is the generalised inverse function defined as
$\psi ^{-1}$
is the generalised inverse function defined as
 $$ \begin{align*} \psi^{-1}(s) = \mathop{\mathrm{sup}}\limits\big\{ r>0 \colon \psi^*(r)=s \big\}. \end{align*} $$
$$ \begin{align*} \psi^{-1}(s) = \mathop{\mathrm{sup}}\limits\big\{ r>0 \colon \psi^*(r)=s \big\}. \end{align*} $$
To study the distribution function of the subordinator
![]() $\mathbf {T}$
, it is convenient to introduce two concentration functions K and h. They are defined as
$\mathbf {T}$
, it is convenient to introduce two concentration functions K and h. They are defined as
 $$ \begin{align} K(r)=\frac{1}{r^2} \int_{(0, r)} s^2 \: \nu({\textrm{d}} s), \quad r> 0, \end{align} $$
$$ \begin{align} K(r)=\frac{1}{r^2} \int_{(0, r)} s^2 \: \nu({\textrm{d}} s), \quad r> 0, \end{align} $$
and
 $$ \begin{align} h(r) = \int_{(0, \infty)} \min{\big\{ 1 , r^{-2} s^2\big\}} \: \nu({\textrm{d}} s), \quad r> 0. \end{align} $$
$$ \begin{align} h(r) = \int_{(0, \infty)} \min{\big\{ 1 , r^{-2} s^2\big\}} \: \nu({\textrm{d}} s), \quad r> 0. \end{align} $$
Notice that
![]() $h(r) \geq K(r)$
. Moreover, by the Fubini–Tonelli theorem, we get
$h(r) \geq K(r)$
. Moreover, by the Fubini–Tonelli theorem, we get
 $$ \begin{align} h(r)=2 \int_r^\infty K(s) s^{-1} {\: \rm d} s. \end{align} $$
$$ \begin{align} h(r)=2 \int_r^\infty K(s) s^{-1} {\: \rm d} s. \end{align} $$
In view of [Reference Grzywny20, Lemma 4], we have
 $$ \begin{align} \frac{1}{24} h(r^{-1} ) \leq \psi^*(r) \leq 2h(r^{-1} ). \end{align} $$
$$ \begin{align} \frac{1}{24} h(r^{-1} ) \leq \psi^*(r) \leq 2h(r^{-1} ). \end{align} $$
A function
![]() $f\colon [0, \infty ) \rightarrow [0, \infty )$
is regularly varying at infinity of index
$f\colon [0, \infty ) \rightarrow [0, \infty )$
is regularly varying at infinity of index
![]() $\alpha $
, if for all
$\alpha $
, if for all
![]() $\lambda \geq 1$
,
$\lambda \geq 1$
,
 $$ \begin{align*} \lim_{x \to \infty} \frac{f(\lambda x)}{f(x)} = \lambda^\alpha. \end{align*} $$
$$ \begin{align*} \lim_{x \to \infty} \frac{f(\lambda x)}{f(x)} = \lambda^\alpha. \end{align*} $$
Analogously, f is regular varying at the origin of index
![]() $\alpha $
if for all
$\alpha $
if for all
![]() $\lambda \geq 1$
,
$\lambda \geq 1$
,
 $$ \begin{align*} \lim_{x \to 0^+} \frac{f(\lambda x)}{f(x)} = \lambda^\alpha. \end{align*} $$
$$ \begin{align*} \lim_{x \to 0^+} \frac{f(\lambda x)}{f(x)} = \lambda^\alpha. \end{align*} $$
If
![]() $\alpha = 0$
, the function f is called slowly varying.
$\alpha = 0$
, the function f is called slowly varying.
We next introduce a notion of scaling conditions frequently used in this article. We say that a function
![]() $f \colon [0,\infty ) \rightarrow [0,\infty )$
has the weak lower scaling property at infinity if there are
$f \colon [0,\infty ) \rightarrow [0,\infty )$
has the weak lower scaling property at infinity if there are
![]() $\alpha \in \mathbb {R}$
,
$\alpha \in \mathbb {R}$
,
![]() $c \in (0,1]$
and
$c \in (0,1]$
and
![]() $x_0 \geq 0$
such that for all
$x_0 \geq 0$
such that for all
![]() $\lambda \geq 1$
and
$\lambda \geq 1$
and
![]() $x> x_0$
,
$x> x_0$
,
We denote it briefly as
![]() $f \in \textrm {WLSC}(\alpha ,c,x_0)$
. Observe that if
$f \in \textrm {WLSC}(\alpha ,c,x_0)$
. Observe that if
![]() $\alpha> \alpha '$
then
$\alpha> \alpha '$
then
![]() $\textrm {WLSC}(\alpha ,c,x_0) \subsetneq \textrm {WLSC}(\alpha ',c,x_0)$
. Analogously, f has the weak upper scaling property at infinity if there are
$\textrm {WLSC}(\alpha ,c,x_0) \subsetneq \textrm {WLSC}(\alpha ',c,x_0)$
. Analogously, f has the weak upper scaling property at infinity if there are
![]() $\beta \in \mathbb {R}$
,
$\beta \in \mathbb {R}$
,
![]() $C \geq 1$
, and
$C \geq 1$
, and
![]() $x_0 \geq 0$
such that for all
$x_0 \geq 0$
such that for all
![]() $\lambda \geq 1$
and
$\lambda \geq 1$
and
![]() $x> x_0$
,
$x> x_0$
,
In this case we write
![]() $f \in \textrm {WUSC}(\beta ,C,x_0)$
.
$f \in \textrm {WUSC}(\beta ,C,x_0)$
.
We say that a function
![]() $f\colon [0, \infty ) \rightarrow [0, \infty )$
has doubling property on
$f\colon [0, \infty ) \rightarrow [0, \infty )$
has doubling property on
![]() $(x_0, \infty )$
for some
$(x_0, \infty )$
for some
![]() $x_0 \geq 0$
if there is
$x_0 \geq 0$
if there is
![]() $C \geq 1$
such that for all
$C \geq 1$
such that for all
![]() $x> x_0$
,
$x> x_0$
,
Notice that a nonincreasing function with the weak lower scaling has a doubling property. Analogously, a nondecreasing function with the weak upper scaling.
A function
![]() $f\colon [0, \infty ) \rightarrow [0, \infty )$
is almost increasing on
$f\colon [0, \infty ) \rightarrow [0, \infty )$
is almost increasing on
![]() $(x_0, \infty )$
for some
$(x_0, \infty )$
for some
![]() $x_0 \geq 0$
if there is
$x_0 \geq 0$
if there is
![]() $c \in (0, 1]$
such that for all
$c \in (0, 1]$
such that for all
![]() $y \geq x> x_0$
,
$y \geq x> x_0$
,
It is almost decreasing on
![]() $(x_0, \infty )$
if there is
$(x_0, \infty )$
if there is
![]() $C \geq 1$
such that for all
$C \geq 1$
such that for all
![]() $y \geq x> x_0$
,
$y \geq x> x_0$
,
In view of [Reference Bogdan, Grzywny and Ryznar6, Lemma 11],
![]() $f \in \textrm {WLSC}(\alpha ,c,x_0)$
if and only if the function
$f \in \textrm {WLSC}(\alpha ,c,x_0)$
if and only if the function
is almost increasing. Similarly,
![]() $f \in \textrm {WUSC}(\beta ,C,x_0)$
if and only if the function
$f \in \textrm {WUSC}(\beta ,C,x_0)$
if and only if the function
is almost decreasing. For a function
![]() $f\colon [0,\infty ) \rightarrow \mathbb {C}$
its Laplace transform is defined as
$f\colon [0,\infty ) \rightarrow \mathbb {C}$
its Laplace transform is defined as
 $$ \begin{align*} \mathcal{L} f(\lambda) = \int_0^\infty e^{-\lambda x} f(x) {\: \rm d} x. \end{align*} $$
$$ \begin{align*} \mathcal{L} f(\lambda) = \int_0^\infty e^{-\lambda x} f(x) {\: \rm d} x. \end{align*} $$
2.1. Bernstein functions
In this section we recall some basic facts about Bernstein functions. A general reference here is the book [Reference Schilling, Song and Vondraček48].
A function
![]() $f\colon (0, \infty ) \rightarrow [0,\infty )$
is completely monotone if it is smooth and
$f\colon (0, \infty ) \rightarrow [0,\infty )$
is completely monotone if it is smooth and
 $$ \begin{align*} {(-1)^n f^{(n)} \geq 0} \end{align*} $$
$$ \begin{align*} {(-1)^n f^{(n)} \geq 0} \end{align*} $$
for all
![]() $n \in \mathbb {N}_0$
. Next, a function
$n \in \mathbb {N}_0$
. Next, a function
![]() $\phi $
is a Bernstein function if it is a nonnegative smooth function such that
$\phi $
is a Bernstein function if it is a nonnegative smooth function such that
![]() $\phi '$
is completely monotone.
$\phi '$
is completely monotone.
Let
![]() $\phi $
be a Bernstein function. In view of [Reference Jacob29, Lemma 3.9.34], for all
$\phi $
be a Bernstein function. In view of [Reference Jacob29, Lemma 3.9.34], for all
![]() $n \in \mathbb {N}$
we have
$n \in \mathbb {N}$
we have
 $$ \begin{align} \phi(\lambda) \geq \frac{(-1)^{n+1}}{n!} \lambda^n \phi^{(n)}(\lambda), \quad \lambda>0. \end{align} $$
$$ \begin{align} \phi(\lambda) \geq \frac{(-1)^{n+1}}{n!} \lambda^n \phi^{(n)}(\lambda), \quad \lambda>0. \end{align} $$
Since
![]() $\phi $
is concave, for each
$\phi $
is concave, for each
![]() $\lambda \geq 1$
and
$\lambda \geq 1$
and
![]() $x> 0$
we have
$x> 0$
we have
thus, by (2.9),
By [Reference Schilling, Song and Vondraček48, Theorem 3.2], there are two nonnegative numbers a and b and a Radon measure
![]() $\mu $
on
$\mu $
on
![]() $(0, \infty )$
satisfying
$(0, \infty )$
satisfying
 $$ \begin{align*} \int_{(0, \infty)} \min{\{1, s \}} \: \mu({\textrm{d}} s) < \infty \end{align*} $$
$$ \begin{align*} \int_{(0, \infty)} \min{\{1, s \}} \: \mu({\textrm{d}} s) < \infty \end{align*} $$
and such that
 $$ \begin{align} \phi(\lambda) = a+b\lambda+ \int_{(0, \infty)} \big(1 - e^{-\lambda s}\big) \: \mu({\textrm{d}} s). \end{align} $$
$$ \begin{align} \phi(\lambda) = a+b\lambda+ \int_{(0, \infty)} \big(1 - e^{-\lambda s}\big) \: \mu({\textrm{d}} s). \end{align} $$
A Bernstein function
![]() $\phi $
is called a complete Bernstein function if the measure
$\phi $
is called a complete Bernstein function if the measure
![]() $\mu $
has a completely monotone density with respect to the Lebesgue measure.
$\mu $
has a completely monotone density with respect to the Lebesgue measure.
Proposition 2.1. Let f be a completely monotone function. Suppose that f has a doubling property on
![]() $(x_0,\infty )$
for some
$(x_0,\infty )$
for some
![]() $x_0\geq 0$
. Then there is
$x_0\geq 0$
. Then there is
![]() $C> 0$
such that for all
$C> 0$
such that for all
![]() $x> x_0$
,
$x> x_0$
,
Proof. Without loss of generality, we can assume
![]() $f \not \equiv 0$
. Clearly,
$f \not \equiv 0$
. Clearly,
 $$ \begin{align*} f(x)-f(x/2)=\int^x_{x/2}f^{\prime}(s) {\: \rm d} s \leq \tfrac{1}{2} x f^{\prime}(x). \end{align*} $$
$$ \begin{align*} f(x)-f(x/2)=\int^x_{x/2}f^{\prime}(s) {\: \rm d} s \leq \tfrac{1}{2} x f^{\prime}(x). \end{align*} $$
Since f is completely monotone, it is a positive function and
 $$ \begin{align*} f(x/2) \geq \tfrac{1}{2} x|f^{\prime}(x)|, \end{align*} $$
$$ \begin{align*} f(x/2) \geq \tfrac{1}{2} x|f^{\prime}(x)|, \end{align*} $$
which, together with the doubling property, gives
for
![]() $x> 2 x_0$
. Hence, we obtain our assertion in the case
$x> 2 x_0$
. Hence, we obtain our assertion in the case
![]() $x_0 = 0$
. If
$x_0 = 0$
. If
![]() $x_0> 0$
, we observe that the function
$x_0> 0$
, we observe that the function
 $$ \begin{align*} [x_0, 2 x_0] \ni x \mapsto \frac{x |f^{\prime}(x)|}{f(x)} \end{align*} $$
$$ \begin{align*} [x_0, 2 x_0] \ni x \mapsto \frac{x |f^{\prime}(x)|}{f(x)} \end{align*} $$
is continuous and positive and thus bounded. This completes the proof.
Proposition 2.2. Let f be a completely monotone function. Suppose that
![]() $-f'\in \textrm {WLSC}(\tau ,c,x_0)$
for some
$-f'\in \textrm {WLSC}(\tau ,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\tau \leq -1$
. Then
$\tau \leq -1$
. Then
![]() $f\in \textrm {WLSC}(1 + \tau ,c,x_0)$
.
$f\in \textrm {WLSC}(1 + \tau ,c,x_0)$
.
Analogously, if
![]() $-f' \in \textrm {WUSC}(\tau ,C,x_0)$
for some
$-f' \in \textrm {WUSC}(\tau ,C,x_0)$
for some
![]() $C \geq 1$
,
$C \geq 1$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\tau \leq -1$
, then
$\tau \leq -1$
, then
![]() $(f-f(\infty )) \in \textrm {WUSC}(\tau ,C,x_0)$
.
$(f-f(\infty )) \in \textrm {WUSC}(\tau ,C,x_0)$
.
Proof. Let
![]() $\lambda>1$
. For
$\lambda>1$
. For
![]() $y> x > x_0$
, we have
$y> x > x_0$
, we have
 $$ \begin{align*} f(\lambda x)-f(\lambda y) = -\int^{\lambda y}_{\lambda x} f'(s) {\: \rm d} s &= -\lambda \int^y_x f'(\lambda s) {\: \rm d} s \\ &\geq - c \lambda^{1+\tau} \int^y_x f'(s) {\: \rm d} s = c \lambda^{1+\tau} (f(x)-f(y)); \end{align*} $$
$$ \begin{align*} f(\lambda x)-f(\lambda y) = -\int^{\lambda y}_{\lambda x} f'(s) {\: \rm d} s &= -\lambda \int^y_x f'(\lambda s) {\: \rm d} s \\ &\geq - c \lambda^{1+\tau} \int^y_x f'(s) {\: \rm d} s = c \lambda^{1+\tau} (f(x)-f(y)); \end{align*} $$
thus,
Since f is nonnegative and nonincreasing, we can take y approaching infinity to get
 $$ \begin{align*} f(\lambda x) &\geq c \lambda^{1+\tau} f(x) + \big(1 - c \lambda^{1+\tau}\big) \lim_{y \to \infty} f(y) \\ &\geq c \lambda^{1+\tau} f(x), \end{align*} $$
$$ \begin{align*} f(\lambda x) &\geq c \lambda^{1+\tau} f(x) + \big(1 - c \lambda^{1+\tau}\big) \lim_{y \to \infty} f(y) \\ &\geq c \lambda^{1+\tau} f(x), \end{align*} $$
where in the last inequality we have also used that
![]() $1 \geq c \lambda ^{1+\tau }$
. The second part of the proposition can be proved in much the same way.
$1 \geq c \lambda ^{1+\tau }$
. The second part of the proposition can be proved in much the same way.
Proposition 2.3. Let
![]() $\phi $
be a Bernstein function with
$\phi $
be a Bernstein function with
![]() $\phi (0)=0$
. Then
$\phi (0)=0$
. Then
![]() $\phi \in \textrm {WLSC}(\alpha ,c,x_0)$
for some
$\phi \in \textrm {WLSC}(\alpha ,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
if and only if
$\alpha>0$
if and only if
![]() $\phi ' \in \textrm {WLSC}(\alpha -1,c',x_0)$
for some
$\phi ' \in \textrm {WLSC}(\alpha -1,c',x_0)$
for some
![]() $c' \in (0,1]$
. Furthermore, if
$c' \in (0,1]$
. Furthermore, if
![]() $\phi \in \textrm {WLSC}(\alpha ,c,x_0)$
, then there is
$\phi \in \textrm {WLSC}(\alpha ,c,x_0)$
, then there is
![]() $C \geq 1$
such that for all
$C \geq 1$
such that for all
![]() $x> x_0$
,
$x> x_0$
,
Proof. Assume first that
![]() $\phi ^{\prime }\in \textrm {WLSC}(\alpha -1,c,x_0)$
. Without loss of generality, we can assume
$\phi ^{\prime }\in \textrm {WLSC}(\alpha -1,c,x_0)$
. Without loss of generality, we can assume
![]() $\phi ^{\prime } \not \equiv 0$
. We claim that (2.12) holds true. In view of (2.9), it is enough to show that there is
$\phi ^{\prime } \not \equiv 0$
. We claim that (2.12) holds true. In view of (2.9), it is enough to show that there is
![]() $C \geq 1$
such that for all
$C \geq 1$
such that for all
![]() $x> x_0$
,
$x> x_0$
,
First, let us observe that, by the weak lower scaling property of
![]() $\phi ^{\prime }$
,
$\phi ^{\prime }$
,
 $$ \begin{align} \nonumber \phi(x) -\phi(x_0) &= \int_{x_0}^{x} \phi^{\prime}(s) {\: \rm d} s \\ \nonumber &\leq c^{-1} \phi^{\prime}(x) \int_{x_0}^x \big(s/x\big)^{-1+\alpha} {\: \rm d} s \\ &\leq \frac{1}{c \alpha} x \phi^{\prime}(x). \end{align} $$
$$ \begin{align} \nonumber \phi(x) -\phi(x_0) &= \int_{x_0}^{x} \phi^{\prime}(s) {\: \rm d} s \\ \nonumber &\leq c^{-1} \phi^{\prime}(x) \int_{x_0}^x \big(s/x\big)^{-1+\alpha} {\: \rm d} s \\ &\leq \frac{1}{c \alpha} x \phi^{\prime}(x). \end{align} $$
Thus, we get the assertion in the case
![]() $x_0 = 0$
. If
$x_0 = 0$
. If
![]() $x_0> 0$
, it is enough to show that there is
$x_0> 0$
, it is enough to show that there is
![]() $C> 0$
such that for all
$C> 0$
such that for all
![]() $x> x_0$
,
$x> x_0$
,
Since
![]() $\phi ' \in \textrm {WLSC}(\alpha -1,c,x_0)$
, the function
$\phi ' \in \textrm {WLSC}(\alpha -1,c,x_0)$
, the function
is almost increasing. Hence, for
![]() $x \geq 2 x_0$
we have
$x \geq 2 x_0$
we have
To conclude (2.14), we notice that
![]() $\phi '(x)$
is positive and continuous in
$\phi '(x)$
is positive and continuous in
![]() $[x_0, 2x_0]$
. Now, by (2.14) we get
$[x_0, 2x_0]$
. Now, by (2.14) we get
for all
![]() $x> x_0$
, which, together with (2.13), implies (2.12) and the scaling property of
$x> x_0$
, which, together with (2.13), implies (2.12) and the scaling property of
![]() $\phi $
follows.
$\phi $
follows.
Now assume that
![]() $\phi \in \textrm {WLSC}(\alpha ,c,x_0)$
. By monotonicity of
$\phi \in \textrm {WLSC}(\alpha ,c,x_0)$
. By monotonicity of
![]() $\phi '$
, for
$\phi '$
, for
![]() $0 < s < t$
,
$0 < s < t$
,
 $$ \begin{align*} \frac{\phi(tx)-\phi(sx)}{\phi(x)} \leq \frac{x(t-s)\phi'(sx)}{\phi(x)}. \end{align*} $$
$$ \begin{align*} \frac{\phi(tx)-\phi(sx)}{\phi(x)} \leq \frac{x(t-s)\phi'(sx)}{\phi(x)}. \end{align*} $$
For
![]() $s=1$
, by the lower scaling we get
$s=1$
, by the lower scaling we get
 $$ \begin{align*} \frac{x(t-1)\phi'(x)}{\phi(x)} \geq \frac{\phi(tx)}{\phi(x)}-1 \geq ct^{\alpha}-1, \end{align*} $$
$$ \begin{align*} \frac{x(t-1)\phi'(x)}{\phi(x)} \geq \frac{\phi(tx)}{\phi(x)}-1 \geq ct^{\alpha}-1, \end{align*} $$
for all
![]() $x>x_0$
. Thus, for
$x>x_0$
. Thus, for
![]() $t = 2^{1/\alpha } c^{-1/\alpha }$
, we obtain that
$t = 2^{1/\alpha } c^{-1/\alpha }$
, we obtain that
![]() $x\phi '(x) \gtrsim \phi (x)$
for all
$x\phi '(x) \gtrsim \phi (x)$
for all
![]() $x>x_0$
. Invoking (2.9), we conclude (2.12). In particular,
$x>x_0$
. Invoking (2.9), we conclude (2.12). In particular,
![]() $\phi '$
has the weak lower scaling property. This completes the proof.
$\phi '$
has the weak lower scaling property. This completes the proof.
Proposition 2.4. Let
![]() $\phi $
be a Bernstein function. Suppose that
$\phi $
be a Bernstein function. Suppose that
![]() $-\phi ^{\prime \prime } \in \textrm {WUSC}(\beta -2,C,x_0)$
for some
$-\phi ^{\prime \prime } \in \textrm {WUSC}(\beta -2,C,x_0)$
for some
![]() $C \geq 1$
,
$C \geq 1$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\beta <1$
. Then for all
$\beta <1$
. Then for all
![]() $x> x_0$
,
$x> x_0$
,
 $$ \begin{align*} \phi'(x) \leq \frac{C}{1-\beta} x(-\phi^{\prime\prime}(x)) + b, \end{align*} $$
$$ \begin{align*} \phi'(x) \leq \frac{C}{1-\beta} x(-\phi^{\prime\prime}(x)) + b, \end{align*} $$
where b is the drift term from the integral representation (2.11) of
![]() $\phi $
.
$\phi $
.
Proof. Without loss of generality, we can assume
![]() $\phi ^{\prime \prime } \not \equiv 0$
. By the scaling property, for
$\phi ^{\prime \prime } \not \equiv 0$
. By the scaling property, for
![]() $x> x_0$
we have
$x> x_0$
we have
 $$ \begin{align*} \frac{\phi'(x)-b}{x(-\phi^{\prime\prime}(x))} = \int_x^{\infty} \frac{t}{x} \frac{(-\phi^{\prime\prime}(t))}{(-\phi^{\prime\prime}(x))} \frac{{\textrm{d}} t}{t} \leq C \int_x^{\infty} \bigg( \frac{t}{x} \bigg)^{-1+\beta} \frac{{\textrm{d}} t}{t} = C \frac{1}{1-\beta}, \end{align*} $$
$$ \begin{align*} \frac{\phi'(x)-b}{x(-\phi^{\prime\prime}(x))} = \int_x^{\infty} \frac{t}{x} \frac{(-\phi^{\prime\prime}(t))}{(-\phi^{\prime\prime}(x))} \frac{{\textrm{d}} t}{t} \leq C \int_x^{\infty} \bigg( \frac{t}{x} \bigg)^{-1+\beta} \frac{{\textrm{d}} t}{t} = C \frac{1}{1-\beta}, \end{align*} $$
which concludes the proof.
Remark 2.5. Let
![]() $\phi $
be a Bernstein function such that
$\phi $
be a Bernstein function such that
![]() $\phi (0) = 0$
. Suppose that
$\phi (0) = 0$
. Suppose that
![]() $-\phi ^{\prime \prime } \in \textrm {WLSC}(\alpha -2,c,x_0)$
, for some
$-\phi ^{\prime \prime } \in \textrm {WLSC}(\alpha -2,c,x_0)$
, for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha \in (0, 1]$
. Since
$\alpha \in (0, 1]$
. Since
![]() $\phi '$
is completely monotone, by Proposition 2.2,
$\phi '$
is completely monotone, by Proposition 2.2,
![]() $\phi ' \in \textrm {WLSC}(\alpha -1,c,x_0)$
. Therefore, by Proposition 2.3, we conclude that
$\phi ' \in \textrm {WLSC}(\alpha -1,c,x_0)$
. Therefore, by Proposition 2.3, we conclude that
![]() $\phi \in \textrm {WLSC}(\alpha ,c_1,x_0)$
for some
$\phi \in \textrm {WLSC}(\alpha ,c_1,x_0)$
for some
![]() $c_1 \in (0, 1]$
.
$c_1 \in (0, 1]$
.
Proposition 2.6. Let f be a completely monotone function. Suppose that
for some
![]() $c \in (0,1]$
,
$c \in (0,1]$
,
![]() $C \geq 1$
,
$C \geq 1$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $0<\alpha \leq \beta <1$
. Then
$0<\alpha \leq \beta <1$
. Then
for some
![]() $c' \in (0,1]$
and
$c' \in (0,1]$
and
![]() $C' \geq 1$
.
$C' \geq 1$
.
Proof. By monotonicity of
![]() $-f'$
, for
$-f'$
, for
![]() $0 < s < t$
,
$0 < s < t$
,
 $$ \begin{align} \frac{-x(t-s)f'(tx)}{f(x)} \leq \frac{f(sx)-f(tx)}{f(x)} \leq \frac{-x(t-s)f'(sx)}{f(x)}. \end{align} $$
$$ \begin{align} \frac{-x(t-s)f'(tx)}{f(x)} \leq \frac{f(sx)-f(tx)}{f(x)} \leq \frac{-x(t-s)f'(sx)}{f(x)}. \end{align} $$
Taking
![]() $s=1$
in the second inequality, the weak upper scaling property yields
$s=1$
in the second inequality, the weak upper scaling property yields
 $$ \begin{align*} \frac{-x(t-1)f'(x)}{f(x)} \geq 1- \frac{f(tx)}{f(x)} \geq 1-ct^{\beta-1}, \end{align*} $$
$$ \begin{align*} \frac{-x(t-1)f'(x)}{f(x)} \geq 1- \frac{f(tx)}{f(x)} \geq 1-ct^{\beta-1}, \end{align*} $$
for all
![]() $x>x_0$
. By selecting
$x>x_0$
. By selecting
![]() $t> 1$
such that
$t> 1$
such that
 $ct^{\beta -1} \leq \frac 12$
, we obtain
$ct^{\beta -1} \leq \frac 12$
, we obtain
 $x\big (-f'(x)\big ) \gtrsim f(x)$
for
$x\big (-f'(x)\big ) \gtrsim f(x)$
for
![]() $x>x_0$
. Similarly, taking
$x>x_0$
. Similarly, taking
![]() $t=1$
in the first inequality in (2.15), by the weak lower scaling property we get
$t=1$
in the first inequality in (2.15), by the weak lower scaling property we get
 $$ \begin{align*} \frac{-x(1-s)f'(x)}{f(x)} \leq \frac{f(sx)}{f(x)}-1 \leq c^{-1}s^{\alpha-1}-1, \end{align*} $$
$$ \begin{align*} \frac{-x(1-s)f'(x)}{f(x)} \leq \frac{f(sx)}{f(x)}-1 \leq c^{-1}s^{\alpha-1}-1, \end{align*} $$
for all
![]() $x>x_0/s$
. By selecting
$x>x_0/s$
. By selecting
![]() $0 < s < 1$
such that
$0 < s < 1$
such that
![]() $s^{\alpha -1}\geq 2c$
, we obtain
$s^{\alpha -1}\geq 2c$
, we obtain
 $x\big ( -f'(x)\big ) \lesssim f(x)$
for
$x\big ( -f'(x)\big ) \lesssim f(x)$
for
![]() $x>x_0/s$
. Hence,
$x>x_0/s$
. Hence,
 $$ \begin{align} f(x) \approx x\big( -f'(x) \big), \end{align} $$
$$ \begin{align} f(x) \approx x\big( -f'(x) \big), \end{align} $$
for all
![]() $x>x_0/s$
. Therefore, lower and upper scaling properties follow from (2.16) and the scaling properties of f. This finishes the proof for the case
$x>x_0/s$
. Therefore, lower and upper scaling properties follow from (2.16) and the scaling properties of f. This finishes the proof for the case
![]() $x_0 = 0$
. If
$x_0 = 0$
. If
![]() $x_0> 0$
, we notice that both f ad
$x_0> 0$
, we notice that both f ad
![]() $-f'$
are positive and continuous; thus, at the possible expense of worsening the constants, we get (2.16) for all
$-f'$
are positive and continuous; thus, at the possible expense of worsening the constants, we get (2.16) for all
![]() $x>x_0$
.
$x>x_0$
.
Now, by combining Propositions 2.3 and 2.6, we immediately get the following corollary.
Corollary 2.7. Let
![]() $\phi $
be a Bernstein function such that
$\phi $
be a Bernstein function such that
![]() $\phi (0)=0$
. Suppose that
$\phi (0)=0$
. Suppose that
for some
![]() $c \in (0,1]$
,
$c \in (0,1]$
,
![]() $C \geq 1$
,
$C \geq 1$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $0<\alpha \leq \beta <1$
. Then
$0<\alpha \leq \beta <1$
. Then
for some
![]() $c' \in (0,1]$
and
$c' \in (0,1]$
and
![]() $C' \geq 1$
.
$C' \geq 1$
.
Lemma 2.8. Let
![]() $\phi $
be a Bernstein function. Suppose that
$\phi $
be a Bernstein function. Suppose that
![]() $-\phi ^{\prime \prime } \in \textrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \textrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
. There is a constant
$\alpha>0$
. There is a constant
![]() $C> 0$
such that for all
$C> 0$
such that for all
![]() $x> x_0$
,
$x> x_0$
,
 $$ \begin{align*} C (-\phi^{\prime\prime}(x)) \leq \int_{(0,1/x)}s^2\mu(ds). \end{align*} $$
$$ \begin{align*} C (-\phi^{\prime\prime}(x)) \leq \int_{(0,1/x)}s^2\mu(ds). \end{align*} $$
Moreover, the constant C depends only on
![]() $\alpha $
and c.
$\alpha $
and c.
Proof. Let
![]() $f\colon (0, \infty ) \rightarrow \mathbb {R}$
be a function defined as
$f\colon (0, \infty ) \rightarrow \mathbb {R}$
be a function defined as
 $$ \begin{align*} f(t)=\int_{(0, t)} s^2 \: \mu ({\textrm{d}} s). \end{align*} $$
$$ \begin{align*} f(t)=\int_{(0, t)} s^2 \: \mu ({\textrm{d}} s). \end{align*} $$
We observe that, by the Fubini–Tonelli theorem, for
![]() $x> 0$
we have
$x> 0$
we have
 $$ \begin{align*} \mathcal{L} f(x) &= \int_0^\infty e^{-x t} \int_{(0, t)} s^2 \: \mu({\textrm{d}} s) {\: \rm d} t \\ &= \int_{(0, \infty)} s^2 \int_s^\infty e^{-x t} {\: \rm d} t \: \mu({\textrm{d}} s) = x^{-1} (-\phi^{\prime\prime}(x)). \end{align*} $$
$$ \begin{align*} \mathcal{L} f(x) &= \int_0^\infty e^{-x t} \int_{(0, t)} s^2 \: \mu({\textrm{d}} s) {\: \rm d} t \\ &= \int_{(0, \infty)} s^2 \int_s^\infty e^{-x t} {\: \rm d} t \: \mu({\textrm{d}} s) = x^{-1} (-\phi^{\prime\prime}(x)). \end{align*} $$
Since f is nondecreasing, for any
![]() $s> 0$
,
$s> 0$
,
 $$ \begin{align*} -\phi^{\prime\prime}(x)=x \mathcal{L} f(x) &\geq \int_s^{\infty} e^{-t} f\big( t/x \big) {\: \rm d} t\\ &\geq e^{-s} f\big(s /x \big). \end{align*} $$
$$ \begin{align*} -\phi^{\prime\prime}(x)=x \mathcal{L} f(x) &\geq \int_s^{\infty} e^{-t} f\big( t/x \big) {\: \rm d} t\\ &\geq e^{-s} f\big(s /x \big). \end{align*} $$
Hence, for any
![]() $u> 2$
,
$u> 2$
,
 $$ \begin{align*} -\phi^{\prime\prime}(x) &=\int_0^u e^{-s} f\big( s/x \big) {\: \rm d} s + \int_u^{\infty} e^{-s} f\big(s/x \big) {\: \rm d} s \\ &\leq f\big(u / x \big) + \int_u^{\infty} e^{-s/2} (-\phi^{\prime\prime}(x/2) ) {\: \rm d} s. \end{align*} $$
$$ \begin{align*} -\phi^{\prime\prime}(x) &=\int_0^u e^{-s} f\big( s/x \big) {\: \rm d} s + \int_u^{\infty} e^{-s} f\big(s/x \big) {\: \rm d} s \\ &\leq f\big(u / x \big) + \int_u^{\infty} e^{-s/2} (-\phi^{\prime\prime}(x/2) ) {\: \rm d} s. \end{align*} $$
Therefore, setting
![]() $x = \lambda u> 2 x_0$
, by the weak lower scaling property of
$x = \lambda u> 2 x_0$
, by the weak lower scaling property of
![]() $-\phi ^{\prime \prime }$
,
$-\phi ^{\prime \prime }$
,
 $$ \begin{align*} f(1/\lambda) &\geq -\phi^{\prime\prime}(u \lambda) - 2 e^{-u/2} (-\phi^{\prime\prime}(u \lambda/2)) \\ &\geq \big(2^{\alpha-2}c - 2 e^{-u/2}\big) (-\phi^{\prime\prime}(u \lambda/2)). \end{align*} $$
$$ \begin{align*} f(1/\lambda) &\geq -\phi^{\prime\prime}(u \lambda) - 2 e^{-u/2} (-\phi^{\prime\prime}(u \lambda/2)) \\ &\geq \big(2^{\alpha-2}c - 2 e^{-u/2}\big) (-\phi^{\prime\prime}(u \lambda/2)). \end{align*} $$
At this stage, we select
![]() $u> 2$
such that
$u> 2$
such that
Then again, by the weak lower scaling property of
![]() $-\phi ^{\prime \prime }$
, for
$-\phi ^{\prime \prime }$
, for
![]() $\lambda>x_0$
,
$\lambda>x_0$
,
which ends the proof.
Lemma 2.9. Let
![]() $\phi $
be a Bernstein function. Suppose that
$\phi $
be a Bernstein function. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
. Then there exists a complete Bernstein function f such that
$\alpha>0$
. Then there exists a complete Bernstein function f such that
![]() $f\approx \phi $
for
$f\approx \phi $
for
![]() $x>0$
and
$x>0$
and
![]() $-f^{\prime \prime }\approx -\phi ^{\prime \prime }$
for
$-f^{\prime \prime }\approx -\phi ^{\prime \prime }$
for
![]() $x>x_0$
.
$x>x_0$
.
Proof. Let us define
 $$ \begin{align*} f(\lambda)=a+b\lambda+\int^\infty_0\frac{\lambda u}{\lambda u +1} \mu({\textrm{d}} u). \end{align*} $$
$$ \begin{align*} f(\lambda)=a+b\lambda+\int^\infty_0\frac{\lambda u}{\lambda u +1} \mu({\textrm{d}} u). \end{align*} $$
By [Reference Schilling, Song and Vondraček48, Theorem 6.2 (vi)] the function f is a complete Bernstein function. Since for
![]() $y> 0$
,
$y> 0$
,
 $$ \begin{align*} \frac{y}{y +1} \approx \big(1-e^{-y}\big), \end{align*} $$
$$ \begin{align*} \frac{y}{y +1} \approx \big(1-e^{-y}\big), \end{align*} $$
we get
![]() $f(\lambda ) \approx \phi (\lambda )$
. Moreover,
$f(\lambda ) \approx \phi (\lambda )$
. Moreover,
 $$ \begin{align*} f^{\prime\prime}(\lambda)=-2\int^\infty_0\frac{u^2}{{(\lambda u+1)^3}}\mu({\textrm{d}}u). \end{align*} $$
$$ \begin{align*} f^{\prime\prime}(\lambda)=-2\int^\infty_0\frac{u^2}{{(\lambda u+1)^3}}\mu({\textrm{d}}u). \end{align*} $$
Hence, by Lemma 2.8 we obtain
![]() $-f^{\prime \prime }(\lambda )\approx -\phi ^{\prime \prime }(\lambda )$
for
$-f^{\prime \prime }(\lambda )\approx -\phi ^{\prime \prime }(\lambda )$
for
![]() $\lambda>x_0$
.
$\lambda>x_0$
.
3. Asymptotic behaviour of densities
Let
![]() $\mathbf {T} = (T_t \colon t \geq 0)$
be a subordinator with the Lévy–Khintchine exponent
$\mathbf {T} = (T_t \colon t \geq 0)$
be a subordinator with the Lévy–Khintchine exponent
![]() $\psi $
and the Laplace exponent
$\psi $
and the Laplace exponent
![]() $\phi $
. Since
$\phi $
. Since
![]() $\phi $
is a Bernstein function, it admits the integral representation (2.11). As it may be easily checked (see, e.g., [Reference Schilling, Song and Vondraček48, Proposition 3.6]), we have
$\phi $
is a Bernstein function, it admits the integral representation (2.11). As it may be easily checked (see, e.g., [Reference Schilling, Song and Vondraček48, Proposition 3.6]), we have
![]() $\mu = \nu $
,
$\mu = \nu $
,
![]() $a = 0$
and
$a = 0$
and
![]() $\psi (\xi ) = \phi (-i\xi )$
. In particular,
$\psi (\xi ) = \phi (-i\xi )$
. In particular,
![]() $\phi (0)=0$
.
$\phi (0)=0$
.
In this section we study the asymptotic behaviour of the probability density of
![]() $T_t$
. In the whole section we assume that
$T_t$
. In the whole section we assume that
![]() $\phi ^{\prime \prime }\not \equiv 0$
; otherwise,
$\phi ^{\prime \prime }\not \equiv 0$
; otherwise,
![]() $T_t=b t$
is deterministic. The main result is Theorem 3.3. Let us start by showing an estimate on the real part of the complex extension
$T_t=b t$
is deterministic. The main result is Theorem 3.3. Let us start by showing an estimate on the real part of the complex extension
![]() $\phi $
.
$\phi $
.
Lemma 3.1. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
. Then there exists
$\alpha>0$
. Then there exists
![]() $C> 0$
such that for all
$C> 0$
such that for all
![]() $w> x_0$
and
$w> x_0$
and
![]() $\lambda \in \mathbb {R}$
,
$\lambda \in \mathbb {R}$
,
 $$ \begin{align*} \Re \big( \phi(w+i\lambda)-\phi(w) \big) \geq C \lambda^2 \big(-\phi^{\prime\prime}(|\lambda| \vee w)\big). \end{align*} $$
$$ \begin{align*} \Re \big( \phi(w+i\lambda)-\phi(w) \big) \geq C \lambda^2 \big(-\phi^{\prime\prime}(|\lambda| \vee w)\big). \end{align*} $$
Proof. By the integral representation (2.11), for
![]() $\lambda \in \mathbb {R}$
we have
$\lambda \in \mathbb {R}$
we have
 $$ \begin{align*} \Re \big( \phi(w+i\lambda)-\phi(w)\big) = \int_{(0, \infty)} \big(1-\cos (\lambda s)\big) e^{-w s} \: \nu ({\textrm{d}} s). \end{align*} $$
$$ \begin{align*} \Re \big( \phi(w+i\lambda)-\phi(w)\big) = \int_{(0, \infty)} \big(1-\cos (\lambda s)\big) e^{-w s} \: \nu ({\textrm{d}} s). \end{align*} $$
In particular,
 $$ \begin{align*} \Re \big( \phi(w+i\lambda)-\phi(w)\big) = \Re \big( \phi(w-i\lambda)-\phi(w)\big). \end{align*} $$
$$ \begin{align*} \Re \big( \phi(w+i\lambda)-\phi(w)\big) = \Re \big( \phi(w-i\lambda)-\phi(w)\big). \end{align*} $$
Thus, it is sufficient to consider
![]() $\lambda> 0$
. We can estimate
$\lambda> 0$
. We can estimate
 $$ \begin{align} \nonumber \Re \big( \phi(w+i\lambda)-\phi(w)\big) &\geq \int_{(0, 1/\lambda)} \big(1-\cos (\lambda s)\big) e^{-w s} \: \nu ({\textrm{d}} s) \\ &\gtrsim \lambda^2 \int_{(0, 1/\lambda)} s^2 e^{-w s} \: \nu({\textrm{d}} s). \end{align} $$
$$ \begin{align} \nonumber \Re \big( \phi(w+i\lambda)-\phi(w)\big) &\geq \int_{(0, 1/\lambda)} \big(1-\cos (\lambda s)\big) e^{-w s} \: \nu ({\textrm{d}} s) \\ &\gtrsim \lambda^2 \int_{(0, 1/\lambda)} s^2 e^{-w s} \: \nu({\textrm{d}} s). \end{align} $$
Due to Lemma 2.8, we obtain, for
![]() $\lambda \geq w$
,
$\lambda \geq w$
,
 $$ \begin{align*} \Re \big( \phi(w+i\lambda)-\phi(w)\big) &\gtrsim \lambda^2 \int_{(0, 1/\lambda)} s^2 \: \nu({\textrm{d}} s)\gtrsim \lambda^2 (-\phi^{\prime\prime}(\lambda)). \end{align*} $$
$$ \begin{align*} \Re \big( \phi(w+i\lambda)-\phi(w)\big) &\gtrsim \lambda^2 \int_{(0, 1/\lambda)} s^2 \: \nu({\textrm{d}} s)\gtrsim \lambda^2 (-\phi^{\prime\prime}(\lambda)). \end{align*} $$
If
![]() $w> \lambda > 0$
, then, by (3.1), we have
$w> \lambda > 0$
, then, by (3.1), we have
 $$ \begin{align*} \Re \big( \phi(w+i\lambda)-\phi(w)\big) &\gtrsim \lambda^2 \int_{(0, 1/w)} s^2 e^{-w s} \nu({\textrm{d}} s) \\ &\geq e^{-1} \lambda^2 \int_{(0,1/w)} s^2 \nu({\textrm{d}} s), \end{align*} $$
$$ \begin{align*} \Re \big( \phi(w+i\lambda)-\phi(w)\big) &\gtrsim \lambda^2 \int_{(0, 1/w)} s^2 e^{-w s} \nu({\textrm{d}} s) \\ &\geq e^{-1} \lambda^2 \int_{(0,1/w)} s^2 \nu({\textrm{d}} s), \end{align*} $$
which, by Lemma 2.8, completes the proof.
Remark 3.2. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
. Since
$\alpha>0$
. Since
by Lemma 2.8 we obtain
for all
![]() $x> x_0$
.
$x> x_0$
.
Theorem 3.3. Let
![]() $\mathbf {T}$
be a subordinator with the Laplace exponent
$\mathbf {T}$
be a subordinator with the Laplace exponent
![]() $\phi $
. Suppose that
$\phi $
. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
. Then the probability distribution of
$\alpha>0$
. Then the probability distribution of
![]() $T_t$
is absolutely continuous for all
$T_t$
is absolutely continuous for all
![]() $t>0$
. If we denote its density by
$t>0$
. If we denote its density by
![]() $p(t, \: \cdot \:)$
, then for each
$p(t, \: \cdot \:)$
, then for each
![]() $\epsilon> 0$
there is
$\epsilon> 0$
there is
![]() $M_0> 0$
such that
$M_0> 0$
such that
 $$ \begin{align*} \left\lvert p\big(t,t\phi'(w)\big) \sqrt{2\pi t(-\phi^{\prime\prime}(w))} \exp{\Big\{t \big( \phi(w)-w \phi'(w) \big) \Big\}} - 1 \right\rvert \leq \epsilon, \end{align*} $$
$$ \begin{align*} \left\lvert p\big(t,t\phi'(w)\big) \sqrt{2\pi t(-\phi^{\prime\prime}(w))} \exp{\Big\{t \big( \phi(w)-w \phi'(w) \big) \Big\}} - 1 \right\rvert \leq \epsilon, \end{align*} $$
provided that
![]() $w> x_0$
and
$w> x_0$
and
![]() $t w^2 (-\phi ^{\prime \prime }(w))> M_0$
.
$t w^2 (-\phi ^{\prime \prime }(w))> M_0$
.
Proof. Let
![]() $x=t \phi '(w)$
and
$x=t \phi '(w)$
and
![]() $M> 0$
. We first show that
$M> 0$
. We first show that
 $$ \begin{align} p(t, x) = \frac{1}{2\pi} \cdot \frac{e^{-t \Phi(x/t,0)}}{\sqrt{t (-\phi^{\prime\prime}(w))}} \int_{\mathbb{R}} \exp{\Bigg\{-t \Bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \Bigg) \Bigg\}} {\: \rm d} u, \end{align} $$
$$ \begin{align} p(t, x) = \frac{1}{2\pi} \cdot \frac{e^{-t \Phi(x/t,0)}}{\sqrt{t (-\phi^{\prime\prime}(w))}} \int_{\mathbb{R}} \exp{\Bigg\{-t \Bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \Bigg) \Bigg\}} {\: \rm d} u, \end{align} $$
provided that
![]() $w> x_0$
and
$w> x_0$
and
![]() $t w^2 (-\phi ^{\prime \prime }(w))> M$
, where for
$t w^2 (-\phi ^{\prime \prime }(w))> M$
, where for
![]() $\lambda \in \mathbb {R}$
we have set
$\lambda \in \mathbb {R}$
we have set
 $$ \begin{align} \Phi \big( x/t, \lambda \big) = \phi(w+i\lambda)-\frac{x}{t}(w+i\lambda). \end{align} $$
$$ \begin{align} \Phi \big( x/t, \lambda \big) = \phi(w+i\lambda)-\frac{x}{t}(w+i\lambda). \end{align} $$
To do so, let us recall that
 $$ \begin{align*} \mathbb{E}\big(e^{-\lambda T_t} \big) = e^{-t \phi(\lambda)}, \quad \lambda \geq 0. \end{align*} $$
$$ \begin{align*} \mathbb{E}\big(e^{-\lambda T_t} \big) = e^{-t \phi(\lambda)}, \quad \lambda \geq 0. \end{align*} $$
Thus, by Mellin’s inversion formula, if the limit
 $$ \begin{align} \lim_{L \to \infty} \frac{1}{2\pi i } \int_{w-i L}^{w+i L} e^{-t \phi(\lambda)+\lambda x} {\: \rm d} \lambda \quad\text{exists,} \end{align} $$
$$ \begin{align} \lim_{L \to \infty} \frac{1}{2\pi i } \int_{w-i L}^{w+i L} e^{-t \phi(\lambda)+\lambda x} {\: \rm d} \lambda \quad\text{exists,} \end{align} $$
then the probability distribution of
![]() $T_t$
has a density
$T_t$
has a density
![]() $p(t, \: \cdot \:)$
and
$p(t, \: \cdot \:)$
and
 $$ \begin{align*} p(t, x) = \lim_{L \to \infty} \frac{1}{2\pi i } \int_{w-i L}^{w+i L} e^{-t \phi(\lambda)+\lambda x} {\: \rm d} \lambda. \end{align*} $$
$$ \begin{align*} p(t, x) = \lim_{L \to \infty} \frac{1}{2\pi i } \int_{w-i L}^{w+i L} e^{-t \phi(\lambda)+\lambda x} {\: \rm d} \lambda. \end{align*} $$
Therefore, our task is to justify the statement (3.4). For
![]() $L> 0$
, we write
$L> 0$
, we write
 $$ \begin{align*} \frac{1}{2 \pi i} \int_{w-i L}^{w+i L} e^{-t \phi(\lambda)+\lambda x} {\: \rm d} \lambda = \frac{1}{2 \pi} \int_{-L}^{L} e^{-t \Phi\left( x/t,\lambda \right)} {\: \rm d} \lambda. \end{align*} $$
$$ \begin{align*} \frac{1}{2 \pi i} \int_{w-i L}^{w+i L} e^{-t \phi(\lambda)+\lambda x} {\: \rm d} \lambda = \frac{1}{2 \pi} \int_{-L}^{L} e^{-t \Phi\left( x/t,\lambda \right)} {\: \rm d} \lambda. \end{align*} $$
By the change of variables
 $$ \begin{align*} \lambda = \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}}, \end{align*} $$
$$ \begin{align*} \lambda = \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}}, \end{align*} $$
we obtain
 $$ \begin{align*} \int_{-L}^{L} e^{-t\Phi\left(x/t,\lambda\right)} {\: \rm d} \lambda &= e^{-t \Phi\left(x/t,0\right)} \int_{-L}^{L} \exp{\Big\{-t \Big( \Phi \big(x/t, \lambda \big)-\Phi\big(x/t, 0\big) \Big)\Big\}} {\: \rm d} \lambda \\ &= \frac{e^{-t \Phi(x/t,0)}}{\sqrt{t (-\phi^{\prime\prime}(w))}} \times \\ &\int_{-L \sqrt{t(-\phi^{\prime\prime}(w))}}^{L \sqrt{t(-\phi^{\prime\prime}(w))}} \exp{\Bigg\{-t \Bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \Bigg) \Bigg\}} {\: \rm d} u. \end{align*} $$
$$ \begin{align*} \int_{-L}^{L} e^{-t\Phi\left(x/t,\lambda\right)} {\: \rm d} \lambda &= e^{-t \Phi\left(x/t,0\right)} \int_{-L}^{L} \exp{\Big\{-t \Big( \Phi \big(x/t, \lambda \big)-\Phi\big(x/t, 0\big) \Big)\Big\}} {\: \rm d} \lambda \\ &= \frac{e^{-t \Phi(x/t,0)}}{\sqrt{t (-\phi^{\prime\prime}(w))}} \times \\ &\int_{-L \sqrt{t(-\phi^{\prime\prime}(w))}}^{L \sqrt{t(-\phi^{\prime\prime}(w))}} \exp{\Bigg\{-t \Bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \Bigg) \Bigg\}} {\: \rm d} u. \end{align*} $$
Let us note here that
![]() $-\phi ^{\prime \prime }$
is nonincreasing and integrable at infinity; thus, we in fact have
$-\phi ^{\prime \prime }$
is nonincreasing and integrable at infinity; thus, we in fact have
![]() $\alpha \leq 1$
. We claim that there is
$\alpha \leq 1$
. We claim that there is
![]() $C> 0$
not depending on M, such that for all
$C> 0$
not depending on M, such that for all
![]() $u \in \mathbb {R}$
,
$u \in \mathbb {R}$
,
 $$ \begin{align} t \Re \Bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \Bigg) \geq C \big( u^2 \wedge ({\lvert {u} \rvert}^\alpha M^{1-\alpha/2})\big), \end{align} $$
$$ \begin{align} t \Re \Bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \Bigg) \geq C \big( u^2 \wedge ({\lvert {u} \rvert}^\alpha M^{1-\alpha/2})\big), \end{align} $$
provided that
![]() $w> x_0$
and
$w> x_0$
and
![]() $t w^2 (-\phi ^{\prime \prime }(w))> M$
. Indeed, by (3.3) and Lemma 3.1, for
$t w^2 (-\phi ^{\prime \prime }(w))> M$
. Indeed, by (3.3) and Lemma 3.1, for
![]() $w> x_0$
we get
$w> x_0$
we get
 $$ \begin{align} t \Re \Bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \Bigg) \gtrsim \frac{{\lvert {u} \rvert}^2}{\phi^{\prime\prime}(w)} \phi^{\prime\prime}\bigg(\frac{{\lvert {u} \rvert}}{\sqrt{t (-\phi^{\prime\prime}(w))}} \vee w\bigg). \end{align} $$
$$ \begin{align} t \Re \Bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \Bigg) \gtrsim \frac{{\lvert {u} \rvert}^2}{\phi^{\prime\prime}(w)} \phi^{\prime\prime}\bigg(\frac{{\lvert {u} \rvert}}{\sqrt{t (-\phi^{\prime\prime}(w))}} \vee w\bigg). \end{align} $$
We next estimate the right-hand side of (3.6). If
 ${\lvert {u} \rvert } \leq w \sqrt {t (-\phi ^{\prime \prime }(w))}$
, then
${\lvert {u} \rvert } \leq w \sqrt {t (-\phi ^{\prime \prime }(w))}$
, then
 $$ \begin{align*} \frac{{\lvert {u} \rvert}^2}{\phi^{\prime\prime}(w)} \phi^{\prime\prime}\bigg(\frac{{\lvert {u} \rvert}}{\sqrt{t (-\phi^{\prime\prime}(w))}} \vee w\bigg) = {\lvert {u} \rvert}^2. \end{align*} $$
$$ \begin{align*} \frac{{\lvert {u} \rvert}^2}{\phi^{\prime\prime}(w)} \phi^{\prime\prime}\bigg(\frac{{\lvert {u} \rvert}}{\sqrt{t (-\phi^{\prime\prime}(w))}} \vee w\bigg) = {\lvert {u} \rvert}^2. \end{align*} $$
Otherwise, since
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
, we obtain
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
, we obtain
 $$ \begin{align*} \frac{{\lvert {u} \rvert}^2}{\phi^{\prime\prime}(w)} \phi^{\prime\prime}\bigg(\frac{{\lvert {u} \rvert}}{\sqrt{t (-\phi^{\prime\prime}(w))}} \vee w\bigg) &\geq c {\lvert {u} \rvert}^2 \bigg(\frac{{\lvert {u} \rvert}}{\sqrt{t w^2 (-\phi^{\prime\prime}(w))}}\bigg)^{-2+\alpha} \\ &= c {\lvert {u} \rvert}^\alpha \big(t w^2 (-\phi^{\prime\prime}(w))\big)^{1-\alpha/2} \\ &\geq c M^{1-\alpha/2} {\lvert {u} \rvert}^\alpha. \end{align*} $$
$$ \begin{align*} \frac{{\lvert {u} \rvert}^2}{\phi^{\prime\prime}(w)} \phi^{\prime\prime}\bigg(\frac{{\lvert {u} \rvert}}{\sqrt{t (-\phi^{\prime\prime}(w))}} \vee w\bigg) &\geq c {\lvert {u} \rvert}^2 \bigg(\frac{{\lvert {u} \rvert}}{\sqrt{t w^2 (-\phi^{\prime\prime}(w))}}\bigg)^{-2+\alpha} \\ &= c {\lvert {u} \rvert}^\alpha \big(t w^2 (-\phi^{\prime\prime}(w))\big)^{1-\alpha/2} \\ &\geq c M^{1-\alpha/2} {\lvert {u} \rvert}^\alpha. \end{align*} $$
Hence, we deduce (3.5). To finish the proof of (3.4), we invoke the dominated convergence theorem. Consequently, by Mellin’s inversion formula we obtain (3.2).
Our next task is to show that for each
![]() $\epsilon> 0$
there is
$\epsilon> 0$
there is
![]() $M_0> 0$
such that
$M_0> 0$
such that
 $$ \begin{align} \Bigg| \int_{\mathbb{R}} \exp{\Bigg\{-t \Bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \Bigg) \Bigg\}}{\: \rm d} u - \int_{\mathbb{R}} e^{-\frac{1}{2} u^2} {\: \rm d} u \Bigg| \leq \epsilon, \end{align} $$
$$ \begin{align} \Bigg| \int_{\mathbb{R}} \exp{\Bigg\{-t \Bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \Bigg) \Bigg\}}{\: \rm d} u - \int_{\mathbb{R}} e^{-\frac{1}{2} u^2} {\: \rm d} u \Bigg| \leq \epsilon, \end{align} $$
provided that
![]() $w> x_0$
and
$w> x_0$
and
![]() $t w^2 (- \phi ^{\prime \prime }(w))> M_0$
. In view of (3.5), by taking
$t w^2 (- \phi ^{\prime \prime }(w))> M_0$
. In view of (3.5), by taking
![]() $M_0>1$
sufficiently large, we get
$M_0>1$
sufficiently large, we get
 $$ \begin{align} \Bigg| \int_{{\lvert {u} \rvert} \geq M_0^{1/4}} \exp{\Bigg\{-t \Bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \Bigg) \Bigg\}} {\: \rm d} u \Bigg| \leq \int_{{\lvert {u} \rvert} \geq M_0^{1/4}} e^{-C |u|^\alpha} {\: \rm d} u \leq \epsilon \end{align} $$
$$ \begin{align} \Bigg| \int_{{\lvert {u} \rvert} \geq M_0^{1/4}} \exp{\Bigg\{-t \Bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \Bigg) \Bigg\}} {\: \rm d} u \Bigg| \leq \int_{{\lvert {u} \rvert} \geq M_0^{1/4}} e^{-C |u|^\alpha} {\: \rm d} u \leq \epsilon \end{align} $$
and
 $$ \begin{align} \int_{{\lvert {u} \rvert} \geq M_0^{1/4}} e^{-\frac{1}{2} u^2} {\: \rm d} u \leq \epsilon. \end{align} $$
$$ \begin{align} \int_{{\lvert {u} \rvert} \geq M_0^{1/4}} e^{-\frac{1}{2} u^2} {\: \rm d} u \leq \epsilon. \end{align} $$
Next, we claim that there is
![]() $C> 0$
such that
$C> 0$
such that
 $$ \begin{align} \bigg| t \bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \bigg) -\frac{1}{2} {\lvert {u} \rvert}^2 \bigg| \leq C {\lvert {u} \rvert}^3 M_0^{-\frac{1}{2}}. \end{align} $$
$$ \begin{align} \bigg| t \bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \bigg) -\frac{1}{2} {\lvert {u} \rvert}^2 \bigg| \leq C {\lvert {u} \rvert}^3 M_0^{-\frac{1}{2}}. \end{align} $$
Indeed, since
 $$ \begin{align*} \partial_\lambda \Phi\left(\frac{x}{t}, 0\right) = 0, \end{align*} $$
$$ \begin{align*} \partial_\lambda \Phi\left(\frac{x}{t}, 0\right) = 0, \end{align*} $$
by Taylor’s formula, we get
 $$ \begin{align} \nonumber \bigg| t \bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \bigg) -\frac{1}{2} {\lvert {u} \rvert}^2 \bigg| &= \bigg| \frac{1}{2} \partial_\lambda^2\Phi \left(\frac{x}{t}, \xi\right) \frac{{\lvert {u} \rvert}^2}{-\phi^{\prime\prime}(w)} - \frac{1}{2} {\lvert {u} \rvert}^2 \bigg| \\ &= \frac{{\lvert {u} \rvert}^2}{2{\lvert {\phi^{\prime\prime}(w)} \rvert}} \big|\phi^{\prime\prime}(w + i \xi) - \phi^{\prime\prime}(w) \big|, \end{align} $$
$$ \begin{align} \nonumber \bigg| t \bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \bigg) -\frac{1}{2} {\lvert {u} \rvert}^2 \bigg| &= \bigg| \frac{1}{2} \partial_\lambda^2\Phi \left(\frac{x}{t}, \xi\right) \frac{{\lvert {u} \rvert}^2}{-\phi^{\prime\prime}(w)} - \frac{1}{2} {\lvert {u} \rvert}^2 \bigg| \\ &= \frac{{\lvert {u} \rvert}^2}{2{\lvert {\phi^{\prime\prime}(w)} \rvert}} \big|\phi^{\prime\prime}(w + i \xi) - \phi^{\prime\prime}(w) \big|, \end{align} $$
where
![]() $\xi $
is some number satisfying
$\xi $
is some number satisfying
 $$ \begin{align} {\lvert {\xi} \rvert} \leq \frac{{\lvert {u} \rvert}}{\sqrt{t(-\phi^{\prime\prime}(w))}}. \end{align} $$
$$ \begin{align} {\lvert {\xi} \rvert} \leq \frac{{\lvert {u} \rvert}}{\sqrt{t(-\phi^{\prime\prime}(w))}}. \end{align} $$
Observe that
 $$ \begin{align*} \big| \phi^{\prime\prime}(w+i\xi)- \phi^{\prime\prime}(w) \big| &\leq \int_{(0, \infty)} s^2 e^{-w s} \big|e^{-i \xi s}-1\big|\: \nu({\textrm{d}} s) \\ &\leq 2 {\lvert {\xi} \rvert} \int_{(0, \infty)} s^3 e^{-w s} \: \nu({\textrm{d}} s) =2 {\lvert {\xi} \rvert} \phi^{\prime\prime\prime}(w). \end{align*} $$
$$ \begin{align*} \big| \phi^{\prime\prime}(w+i\xi)- \phi^{\prime\prime}(w) \big| &\leq \int_{(0, \infty)} s^2 e^{-w s} \big|e^{-i \xi s}-1\big|\: \nu({\textrm{d}} s) \\ &\leq 2 {\lvert {\xi} \rvert} \int_{(0, \infty)} s^3 e^{-w s} \: \nu({\textrm{d}} s) =2 {\lvert {\xi} \rvert} \phi^{\prime\prime\prime}(w). \end{align*} $$
Since
![]() $-\phi ^{\prime \prime }$
is a nonincreasing function with the weak lower scaling property, it is doubling. Thus, by Proposition 2.1, for
$-\phi ^{\prime \prime }$
is a nonincreasing function with the weak lower scaling property, it is doubling. Thus, by Proposition 2.1, for
![]() $w> x_0$
,
$w> x_0$
,
which together with (3.12) give
 $$ \begin{align} \nonumber \big| \phi^{\prime\prime}(w + i \xi) - \phi^{\prime\prime}(w) \big| &\leq C \frac{{\lvert {u} \rvert}}{\sqrt{t (-\phi^{\prime\prime}(w))}} \cdot \frac{-\phi^{\prime\prime}(w)}{w} \\ &\leq C M_0^{-\frac{1}{2}} {\lvert {u} \rvert} (-\phi^{\prime\prime}(w)), \end{align} $$
$$ \begin{align} \nonumber \big| \phi^{\prime\prime}(w + i \xi) - \phi^{\prime\prime}(w) \big| &\leq C \frac{{\lvert {u} \rvert}}{\sqrt{t (-\phi^{\prime\prime}(w))}} \cdot \frac{-\phi^{\prime\prime}(w)}{w} \\ &\leq C M_0^{-\frac{1}{2}} {\lvert {u} \rvert} (-\phi^{\prime\prime}(w)), \end{align} $$
whenever
![]() $t w^2 (-\phi ^{\prime \prime }(w))> M_0$
. Now, (3.10) easily follows by (3.13) and (3.11).
$t w^2 (-\phi ^{\prime \prime }(w))> M_0$
. Now, (3.10) easily follows by (3.13) and (3.11).
Finally, since for any
![]() $z \in \mathbb {C}$
,
$z \in \mathbb {C}$
,
 $$ \begin{align*} \big|e^z - 1\big| \leq {\lvert {z} \rvert} e^{\lvert {z} \rvert}, \end{align*} $$
$$ \begin{align*} \big|e^z - 1\big| \leq {\lvert {z} \rvert} e^{\lvert {z} \rvert}, \end{align*} $$
by (3.10) we obtain
 $$ \begin{align*} & \Bigg| \int_{{\lvert {u} \rvert} \leq M_0^{1/4}} \exp{\Bigg\{-t \Bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \Bigg) \Bigg\}} - e^{-\frac{1}{2} {\lvert {u} \rvert}^2} {\: \rm d} u \Bigg| \\ &\qquad\qquad\leq C M_0^{-\frac{1}{2}} \int_{{\lvert {u} \rvert} \leq M_0^{1/4}} \exp\bigg\{-\tfrac{1}{2} {\lvert {u} \rvert}^2 + C M_0^{-\frac{1}{2}} {\lvert {u} \rvert}^3\bigg\} {\lvert {u} \rvert}^3 {\: \rm d} u \leq \epsilon, \end{align*} $$
$$ \begin{align*} & \Bigg| \int_{{\lvert {u} \rvert} \leq M_0^{1/4}} \exp{\Bigg\{-t \Bigg( \Phi \bigg(\frac{x}{t}, \frac{u}{\sqrt{t (-\phi^{\prime\prime}(w))}} \bigg) - \Phi\bigg(\frac{x}{t}, 0\bigg) \Bigg) \Bigg\}} - e^{-\frac{1}{2} {\lvert {u} \rvert}^2} {\: \rm d} u \Bigg| \\ &\qquad\qquad\leq C M_0^{-\frac{1}{2}} \int_{{\lvert {u} \rvert} \leq M_0^{1/4}} \exp\bigg\{-\tfrac{1}{2} {\lvert {u} \rvert}^2 + C M_0^{-\frac{1}{2}} {\lvert {u} \rvert}^3\bigg\} {\lvert {u} \rvert}^3 {\: \rm d} u \leq \epsilon, \end{align*} $$
provided that
![]() $M_0$
is sufficiently large, which, together with (3.8) and (3.9), completes the proof of (3.7) and the theorem follows.
$M_0$
is sufficiently large, which, together with (3.8) and (3.9), completes the proof of (3.7) and the theorem follows.
Remark 3.4. If
![]() $x_0 = 0$
, then the constant
$x_0 = 0$
, then the constant
![]() $M_0$
in Theorem 3.3 depends only on
$M_0$
in Theorem 3.3 depends only on
![]() $\alpha $
and c. If
$\alpha $
and c. If
![]() $x_0> 0$
, it also depends on
$x_0> 0$
, it also depends on
 $$ \begin{align*} \mathop{\mathrm{sup}}\limits_{x \in [x_0, 2 x_0]} \frac{x \phi^{\prime\prime\prime}(x)}{-\phi^{\prime\prime}(x)}. \end{align*} $$
$$ \begin{align*} \mathop{\mathrm{sup}}\limits_{x \in [x_0, 2 x_0]} \frac{x \phi^{\prime\prime\prime}(x)}{-\phi^{\prime\prime}(x)}. \end{align*} $$
By Theorem 3.3, we immediately get the following corollaries.
Corollary 3.5. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
. Then there is
$\alpha>0$
. Then there is
![]() $M_0> 0$
such that
$M_0> 0$
such that
 $$ \begin{align*} p(t,x) \approx \frac{1}{\sqrt{t (-\phi^{\prime\prime} (w))}} \exp\Big\{-t \big(\phi(w) - w \phi'(w)\big)\Big\}, \end{align*} $$
$$ \begin{align*} p(t,x) \approx \frac{1}{\sqrt{t (-\phi^{\prime\prime} (w))}} \exp\Big\{-t \big(\phi(w) - w \phi'(w)\big)\Big\}, \end{align*} $$
uniformly on the set
 $$ \begin{align*} \Big\{ (t, x) \in \mathbb{R}_+ \times \mathbb{R} \colon tb < x < t \phi'(x_0^+) \text{ and } t w^2 (-\phi^{\prime\prime}(w))> M_0 \Big\}, \end{align*} $$
$$ \begin{align*} \Big\{ (t, x) \in \mathbb{R}_+ \times \mathbb{R} \colon tb < x < t \phi'(x_0^+) \text{ and } t w^2 (-\phi^{\prime\prime}(w))> M_0 \Big\}, \end{align*} $$
where
![]() $w = (\phi ')^{-1}(x/t)$
.
$w = (\phi ')^{-1}(x/t)$
.
Corollary 3.6. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
. Assume also that
$\alpha>0$
. Assume also that
![]() $b = 0$
. Then for any
$b = 0$
. Then for any
![]() $x>0$
,
$x>0$
,
 $$ \begin{align*} \lim_{t\to\infty} p(t,x) \sqrt{t (-\phi^{\prime\prime} (w))} \exp\Big\{t \big(\phi(w) - w \phi'(w)\big)\Big\} = (2\pi)^{-1/2}, \end{align*} $$
$$ \begin{align*} \lim_{t\to\infty} p(t,x) \sqrt{t (-\phi^{\prime\prime} (w))} \exp\Big\{t \big(\phi(w) - w \phi'(w)\big)\Big\} = (2\pi)^{-1/2}, \end{align*} $$
where
![]() $w = (\phi ')^{-1}(x/t)$
.
$w = (\phi ')^{-1}(x/t)$
.
By imposing on
![]() $-\phi ^{\prime \prime }$
an additional condition of the weak upper scaling, we can further simplify the description of the set where the sharp estimates on
$-\phi ^{\prime \prime }$
an additional condition of the weak upper scaling, we can further simplify the description of the set where the sharp estimates on
![]() $p(t, x)$
hold.
$p(t, x)$
hold.
Corollary 3.7. Suppose that
![]() $\phi \in \mathrm {WLSC}(\alpha ,c,x_0) \cap \mathrm {WUSC}(\beta ,C,x_0)$
for some
$\phi \in \mathrm {WLSC}(\alpha ,c,x_0) \cap \mathrm {WUSC}(\beta ,C,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $C \geq 1$
,
$C \geq 1$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $0 < \alpha \leq \beta < 1$
. Assume also that
$0 < \alpha \leq \beta < 1$
. Assume also that
![]() $b = 0$
. Then there is
$b = 0$
. Then there is
![]() $\delta> 0$
such that
$\delta> 0$
such that
 $$ \begin{align*} p(t, x) \approx \frac{1}{\sqrt{t (-\phi^{\prime\prime} (w))}} \exp\Big\{-t \big(\phi(w) - w \phi'(w)\big)\Big\}, \end{align*} $$
$$ \begin{align*} p(t, x) \approx \frac{1}{\sqrt{t (-\phi^{\prime\prime} (w))}} \exp\Big\{-t \big(\phi(w) - w \phi'(w)\big)\Big\}, \end{align*} $$
uniformly on the set
 $$ \begin{align} \Big\{ (t, x) \in \mathbb{R}_+ \times \mathbb{R} \colon 0 < x \phi^{-1}(1/t) < \delta, \text{ and } 0 \leq t \phi(x_0) \leq 1 \Big\}, \end{align} $$
$$ \begin{align} \Big\{ (t, x) \in \mathbb{R}_+ \times \mathbb{R} \colon 0 < x \phi^{-1}(1/t) < \delta, \text{ and } 0 \leq t \phi(x_0) \leq 1 \Big\}, \end{align} $$
where
![]() $w = (\phi ')^{-1}(x/t)$
.
$w = (\phi ')^{-1}(x/t)$
.
Proof. By Proposition 2.3, there is
![]() $C_1 \geq 1$
such that for all
$C_1 \geq 1$
such that for all
![]() $u> x_0$
,
$u> x_0$
,
thus, for
![]() $(t, x)$
belonging to the set (3.14),
$(t, x)$
belonging to the set (3.14),
 $$ \begin{align} \nonumber \frac{x}{t} < \delta \frac{1}{t \phi^{-1}(1/t)} &= \delta \frac{\phi\big(\phi^{-1}(1/t) \big)}{\phi^{-1}(1/t)} \\ &\leq C_1 \delta \phi'\big(\phi^{-1}(1/t)\big). \end{align} $$
$$ \begin{align} \nonumber \frac{x}{t} < \delta \frac{1}{t \phi^{-1}(1/t)} &= \delta \frac{\phi\big(\phi^{-1}(1/t) \big)}{\phi^{-1}(1/t)} \\ &\leq C_1 \delta \phi'\big(\phi^{-1}(1/t)\big). \end{align} $$
By Proposition 2.3,
![]() $\phi ' \in \mathrm {WLSC}(-1+\alpha ,c,x_0)$
; hence, for all
$\phi ' \in \mathrm {WLSC}(-1+\alpha ,c,x_0)$
; hence, for all
![]() $D \geq 1$
,
$D \geq 1$
,
 $$ \begin{align*} \phi'\big(D \phi^{-1}(1/t)\big) \geq c D^{-1+\alpha} \phi'\big(\phi^{-1}(1/t)\big). \end{align*} $$
$$ \begin{align*} \phi'\big(D \phi^{-1}(1/t)\big) \geq c D^{-1+\alpha} \phi'\big(\phi^{-1}(1/t)\big). \end{align*} $$
By taking
![]() $\delta $
sufficiently small, we get
$\delta $
sufficiently small, we get
 $$ \begin{align*} D = \bigg(\frac{c}{C_1 \delta}\bigg)^{\frac{1}{1-\alpha}} \geq 1; \end{align*} $$
$$ \begin{align*} D = \bigg(\frac{c}{C_1 \delta}\bigg)^{\frac{1}{1-\alpha}} \geq 1; \end{align*} $$
thus, by (3.15), we obtain
 $$ \begin{align*} \frac{x}{t} < \phi'\big(D \phi^{-1}(1/t) \big), \end{align*} $$
$$ \begin{align*} \frac{x}{t} < \phi'\big(D \phi^{-1}(1/t) \big), \end{align*} $$
which implies that
In particular,
![]() $w> x_0$
. On the other hand, by Propositions 2.3 and 2.4, there is
$w> x_0$
. On the other hand, by Propositions 2.3 and 2.4, there is
![]() $c_1 \in (0,1]$
such that
$c_1 \in (0,1]$
such that
By Remark 2.5,
![]() $\phi \in \mathrm {WLSC}(\alpha ,c_2,x_0)$
for some
$\phi \in \mathrm {WLSC}(\alpha ,c_2,x_0)$
for some
![]() $c_2 \in (0,1]$
. Therefore,
$c_2 \in (0,1]$
. Therefore,
 $$ \begin{align*} t\phi(w) = \frac{\phi(w)}{\phi \big( \phi^{-1}(1/t) \big)} \geq c_2 \Bigg( \frac{w} {\phi^{-1}(1/t)} \Bigg)^{\alpha}, \end{align*} $$
$$ \begin{align*} t\phi(w) = \frac{\phi(w)}{\phi \big( \phi^{-1}(1/t) \big)} \geq c_2 \Bigg( \frac{w} {\phi^{-1}(1/t)} \Bigg)^{\alpha}, \end{align*} $$
which, together with (3.16), gives
for
![]() $\delta $
sufficiently small. Hence, by Corollary 3.5, we conclude the proof.
$\delta $
sufficiently small. Hence, by Corollary 3.5, we conclude the proof.
The following proposition provides a sufficient condition on the measure
![]() $\nu $
that entails the weak lower scaling property of
$\nu $
that entails the weak lower scaling property of
![]() $-\phi ^{\prime \prime }$
and allows us to apply Theorem 3.3.
$-\phi ^{\prime \prime }$
and allows us to apply Theorem 3.3.
Proposition 3.8. Suppose that there are
![]() $x_0 \geq 0$
,
$x_0 \geq 0$
,
![]() $C \geq 1$
and
$C \geq 1$
and
![]() $\alpha> 0$
such that for all
$\alpha> 0$
such that for all
![]() $0 < r < 1/x_0$
and
$0 < r < 1/x_0$
and
![]() $0 < \lambda \leq 1$
,
$0 < \lambda \leq 1$
,
 $$ \begin{align} \nu\big((r,\infty)\big) \leq C\lambda^{\alpha}\nu\big((\lambda r,\infty)\big). \end{align} $$
$$ \begin{align} \nu\big((r,\infty)\big) \leq C\lambda^{\alpha}\nu\big((\lambda r,\infty)\big). \end{align} $$
Then
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
.
$c \in (0, 1]$
.
Proof. Let us first notice that by the Fubini–Tonelli theorem,
 $$ \begin{align*} h(r) &= r^{-2} \int_{(0, \infty)} \min\big\{r^2, s^2\big\} \nu({\textrm{d}} s) \\ &= r^{-2} \int_0^r t \nu\big((t,\infty)\big) {\: \rm d} t. \end{align*} $$
$$ \begin{align*} h(r) &= r^{-2} \int_{(0, \infty)} \min\big\{r^2, s^2\big\} \nu({\textrm{d}} s) \\ &= r^{-2} \int_0^r t \nu\big((t,\infty)\big) {\: \rm d} t. \end{align*} $$
Thus, by (3.17), for all
![]() $0 < r < 1/x_0$
and
$0 < r < 1/x_0$
and
![]() $0 < \lambda \leq 1$
,
$0 < \lambda \leq 1$
,
 $$ \begin{align} \nonumber C\lambda^{\alpha}h(\lambda r) &= \frac{2C\lambda^{\alpha}}{r^2} \int_0^r t\nu\big((\lambda t,\infty)\big) {\: \rm d} t \\ \nonumber &\geq \frac{2}{r^2}\int_0^r t\nu\big((t,\infty)\big) {\: \rm d} t \\ &=h(r). \end{align} $$
$$ \begin{align} \nonumber C\lambda^{\alpha}h(\lambda r) &= \frac{2C\lambda^{\alpha}}{r^2} \int_0^r t\nu\big((\lambda t,\infty)\big) {\: \rm d} t \\ \nonumber &\geq \frac{2}{r^2}\int_0^r t\nu\big((t,\infty)\big) {\: \rm d} t \\ &=h(r). \end{align} $$
Hence, by [Reference Grzywny and Szczypkowski23, Lemma 2.3], there is
![]() $C' \geq 1$
such that for all
$C' \geq 1$
such that for all
![]() $0 < r <1/x_0$
,
$0 < r <1/x_0$
,
The integral representation of
![]() $\phi $
entails that
$\phi $
entails that
thus, by (3.19), we obtain
for all
![]() $x> x_0$
. Now, the weak lower scaling property of
$x> x_0$
. Now, the weak lower scaling property of
![]() $-\phi ^{\prime \prime }$
is a consequence of (3.18).
$-\phi ^{\prime \prime }$
is a consequence of (3.18).
4. Estimates on the density
Let
![]() $\mathbf {T} = (T_t \colon t \geq 0)$
be a subordinator with the Lévy–Khintchine exponent
$\mathbf {T} = (T_t \colon t \geq 0)$
be a subordinator with the Lévy–Khintchine exponent
![]() $\psi $
and the Laplace exponent
$\psi $
and the Laplace exponent
![]() $\phi $
. In this section we always assume that
$\phi $
. In this section we always assume that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha \in (0, 1]$
. In particular, by Theorem 3.3, the probability distribution of
$\alpha \in (0, 1]$
. In particular, by Theorem 3.3, the probability distribution of
![]() $T_t$
has a density
$T_t$
has a density
![]() $p(t, \: \cdot \:)$
. To express the majorant on
$p(t, \: \cdot \:)$
. To express the majorant on
![]() $p(t, \: \cdot \:)$
, it is convenient to set
$p(t, \: \cdot \:)$
, it is convenient to set
Obviously,
![]() $\varphi \in \mathrm {WLSC}(\alpha ,c,x_0)$
. Let
$\varphi \in \mathrm {WLSC}(\alpha ,c,x_0)$
. Let
![]() $\varphi ^{-1}$
denote the generalised inverse function defined as
$\varphi ^{-1}$
denote the generalised inverse function defined as
 $$ \begin{align*} \varphi^{-1}(x) = \mathop{\mathrm{sup}}\limits \big\{r> 0 \colon \varphi^*(r) = x \big\} \end{align*} $$
$$ \begin{align*} \varphi^{-1}(x) = \mathop{\mathrm{sup}}\limits \big\{r> 0 \colon \varphi^*(r) = x \big\} \end{align*} $$
where
 $$ \begin{align*} \varphi^*(r) = \mathop{\mathrm{sup}}\limits_{0 < x \leq r} \varphi(x). \end{align*} $$
$$ \begin{align*} \varphi^*(r) = \mathop{\mathrm{sup}}\limits_{0 < x \leq r} \varphi(x). \end{align*} $$
We start by showing comparability between the two concentration functions K and h defined in (2.3) and (2.4), respectively.
Proposition 4.1. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
. Then there is
$\alpha>0$
. Then there is
![]() $C \geq 1$
such that for all
$C \geq 1$
such that for all
![]() $0 < r < 1/x_0$
,
$0 < r < 1/x_0$
,
Proof. Since
![]() $h(r) \geq K(r)$
, it is enough to show that for some
$h(r) \geq K(r)$
, it is enough to show that for some
![]() $C \geq 1$
and
$C \geq 1$
and
![]() $0 < r < 1/x_0$
,
$0 < r < 1/x_0$
,
In view of (2.5), we have
 $$ \begin{align} h(r) = 2 \int_r^\infty K(s) \frac{{\textrm{d}} s}{s} = 2 \int_r^{1/x_0} K(s) \frac{{\textrm{d}} s}{s} + 2 \int_{1/x_0}^{\infty} K(s) \frac{{\textrm{d}} s}{s}. \end{align} $$
$$ \begin{align} h(r) = 2 \int_r^\infty K(s) \frac{{\textrm{d}} s}{s} = 2 \int_r^{1/x_0} K(s) \frac{{\textrm{d}} s}{s} + 2 \int_{1/x_0}^{\infty} K(s) \frac{{\textrm{d}} s}{s}. \end{align} $$
Let us consider the first term on the right-hand side of (4.1). By Remark 3.2 we have
![]() $K(r) \approx \varphi (1/r)$
, for
$K(r) \approx \varphi (1/r)$
, for
![]() $0<r<1/x_0$
, which implies
$0<r<1/x_0$
, which implies
 $$ \begin{align*} \int_r^{1/x_0} K(s) \frac{{\textrm{d}} s}{s} \lesssim K(r), \quad 0<r<1/x_0. \end{align*} $$
$$ \begin{align*} \int_r^{1/x_0} K(s) \frac{{\textrm{d}} s}{s} \lesssim K(r), \quad 0<r<1/x_0. \end{align*} $$
This finishes the proof in the case
![]() $x_0 = 0$
. If
$x_0 = 0$
. If
![]() $x_0> 0$
, then, for
$x_0> 0$
, then, for
![]() $1/(2x_0)\leq r<1/x_0$
, we have
$1/(2x_0)\leq r<1/x_0$
, we have
Hence,
![]() $K(r) \gtrsim 1$
for all
$K(r) \gtrsim 1$
for all
![]() $0 < r < 1/x_0$
. Since the second term on the right-hand side of (4.1) is constant, the proof is completed.
$0 < r < 1/x_0$
. Since the second term on the right-hand side of (4.1) is constant, the proof is completed.
Let us notice that by (2.6), Proposition 4.1 and Remark 3.2, we have
for all
![]() $x> x_0$
. In particular, there is
$x> x_0$
. In particular, there is
![]() $c_1 \in (0, 1]$
such that
$c_1 \in (0, 1]$
such that
![]() $\psi ^* \in \mathrm {WLSC}(\alpha ,c_1,x_0)$
. Moreover,
$\psi ^* \in \mathrm {WLSC}(\alpha ,c_1,x_0)$
. Moreover,
 $$ \begin{align*} \psi^*(x) \lesssim K(1/x) &= x^2 \int_{(0, 1/x)} s^2 \: \nu({\textrm{d}} s) \\ &\lesssim \int_{(0, 1/x)} \big(1 - \cos s x\big) \: \nu({\textrm{d}} s); \end{align*} $$
$$ \begin{align*} \psi^*(x) \lesssim K(1/x) &= x^2 \int_{(0, 1/x)} s^2 \: \nu({\textrm{d}} s) \\ &\lesssim \int_{(0, 1/x)} \big(1 - \cos s x\big) \: \nu({\textrm{d}} s); \end{align*} $$
thus, for all
![]() $x> x_0$
,
$x> x_0$
,
Since for
![]() $\lambda \geq 1$
and
$\lambda \geq 1$
and
![]() $x> 0$
,
$x> 0$
,
we get
Proposition 4.2. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
. Then for all
$\alpha>0$
. Then for all
![]() $r> 2 h(1/x_0)$
,
$r> 2 h(1/x_0)$
,
 $$ \begin{align} \frac{1}{h^{-1}(r)} \approx \psi^{-1}(r). \end{align} $$
$$ \begin{align} \frac{1}{h^{-1}(r)} \approx \psi^{-1}(r). \end{align} $$
Furthermore, there is
![]() $C \geq 1$
such that for all
$C \geq 1$
such that for all
![]() $\lambda \geq 1$
and
$\lambda \geq 1$
and
![]() $r> 2 h(1/x_0)$
,
$r> 2 h(1/x_0)$
,
 $$ \begin{align*} \psi^{-1}(\lambda r) \leq C \lambda^{1/\alpha} \psi^{-1}(r). \end{align*} $$
$$ \begin{align*} \psi^{-1}(\lambda r) \leq C \lambda^{1/\alpha} \psi^{-1}(r). \end{align*} $$
Proof. Using (2.6), we immediately get
 $$ \begin{align*} \frac{1}{h^{-1}(r/2)} \leq \psi^{-1}(r) \leq \frac{1}{h^{-1}(24 r)} \end{align*} $$
$$ \begin{align*} \frac{1}{h^{-1}(r/2)} \leq \psi^{-1}(r) \leq \frac{1}{h^{-1}(24 r)} \end{align*} $$
for all
![]() $r>0$
. On the other hand, by Proposition 4.1 and [Reference Grzywny and Szczypkowski23, Lemma 2.3], there is
$r>0$
. On the other hand, by Proposition 4.1 and [Reference Grzywny and Szczypkowski23, Lemma 2.3], there is
![]() $C \geq 1$
such that for all
$C \geq 1$
such that for all
![]() $\lambda \geq 1$
and
$\lambda \geq 1$
and
![]() $r> h(1/x_0)$
,
$r> h(1/x_0)$
,
 $$ \begin{align} \frac{1}{h^{-1}(\lambda r)} \leq C \lambda^{1/\alpha} \frac{1}{h^{-1}(r)}. \end{align} $$
$$ \begin{align} \frac{1}{h^{-1}(\lambda r)} \leq C \lambda^{1/\alpha} \frac{1}{h^{-1}(r)}. \end{align} $$
Hence, for
![]() $r> 2 h(1/x_0)$
,
$r> 2 h(1/x_0)$
,
 $$ \begin{align} C^{-1} 2^{-1/\alpha} \frac{1}{h^{-1}(r)} \leq \psi^{-1}(r) \leq C (24)^{1/\alpha} \frac{1}{h^{-1}(r)}, \end{align} $$
$$ \begin{align} C^{-1} 2^{-1/\alpha} \frac{1}{h^{-1}(r)} \leq \psi^{-1}(r) \leq C (24)^{1/\alpha} \frac{1}{h^{-1}(r)}, \end{align} $$
proving (4.6). The weak upper scaling property of
![]() $\psi ^{-1}$
is a consequence of (4.7) and (4.8).
$\psi ^{-1}$
is a consequence of (4.7) and (4.8).
Proposition 4.3. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
. Then for all
$\alpha>0$
. Then for all
![]() $x> x_0$
,
$x> x_0$
,
and for all
![]() $r> \varphi (x_0)$
,
$r> \varphi (x_0)$
,
Furthermore, there is
![]() $C \geq 1$
such that for all
$C \geq 1$
such that for all
![]() $\lambda \geq 1$
and
$\lambda \geq 1$
and
![]() $r> \varphi (x_0)$
,
$r> \varphi (x_0)$
,
 $$ \begin{align*} \varphi^{-1}(\lambda r) \leq C \lambda^{1/\alpha} \varphi^{-1}(r). \end{align*} $$
$$ \begin{align*} \varphi^{-1}(\lambda r) \leq C \lambda^{1/\alpha} \varphi^{-1}(r). \end{align*} $$
Proof. We start by showing that there is
![]() $C \geq 1$
such that for all
$C \geq 1$
such that for all
![]() $x> x_0$
,
$x> x_0$
,
The first inequality in (4.11) immediately follows from (4.2). If
![]() $x_0 = 0$
, then the second inequality is also the consequence of (4.2). In the case
$x_0 = 0$
, then the second inequality is also the consequence of (4.2). In the case
![]() $x_0> 0$
, we observe that for
$x_0> 0$
, we observe that for
![]() $x> x_0$
, we have
$x> x_0$
, we have
 $$ \begin{align*} \varphi^*(x) &= \max{\Big\{\mathop{\mathrm{sup}}\limits_{0 < y \leq x_0} \varphi(y), \mathop{\mathrm{sup}}\limits_{x_0 \leq y \leq x} \varphi(y)\Big\}} \\ &\lesssim \max{\big\{\varphi^*(x_0), \psi^*(x)\big\}} \\ &\leq \bigg(1 + \frac{\varphi^*(x_0)}{\psi^*(x_0)}\bigg)\psi^*(x), \end{align*} $$
$$ \begin{align*} \varphi^*(x) &= \max{\Big\{\mathop{\mathrm{sup}}\limits_{0 < y \leq x_0} \varphi(y), \mathop{\mathrm{sup}}\limits_{x_0 \leq y \leq x} \varphi(y)\Big\}} \\ &\lesssim \max{\big\{\varphi^*(x_0), \psi^*(x)\big\}} \\ &\leq \bigg(1 + \frac{\varphi^*(x_0)}{\psi^*(x_0)}\bigg)\psi^*(x), \end{align*} $$
proving (4.11).
Now, using (4.11), we easily get
for all
![]() $r> C \psi ^*(x_0)$
. Hence, by Proposition 4.2,
$r> C \psi ^*(x_0)$
. Hence, by Proposition 4.2,
for
 $r> C \max {\big \{\psi ^*(x_0), 2 h(1/x_0)\big \}}$
. Finally, since both
$r> C \max {\big \{\psi ^*(x_0), 2 h(1/x_0)\big \}}$
. Finally, since both
![]() $\psi ^{-1}$
and
$\psi ^{-1}$
and
![]() $\varphi ^{-1}$
are positive and continuous, at the possible expense of worsening the constant, we can extend the area of comparability to conclude (4.10). Now, the scaling property of
$\varphi ^{-1}$
are positive and continuous, at the possible expense of worsening the constant, we can extend the area of comparability to conclude (4.10). Now, the scaling property of
![]() $\varphi ^{-1}$
follows by (4.10) and Proposition 4.2.
$\varphi ^{-1}$
follows by (4.10) and Proposition 4.2.
Remark 4.4. Note that, alternatively, one can define the (left-sided) generalised inverse
where
 $$ \begin{align*} \varphi_*(r) = \inf_{r \leq x} \varphi(x). \end{align*} $$
$$ \begin{align*} \varphi_*(r) = \inf_{r \leq x} \varphi(x). \end{align*} $$
In such a case we have
 $$ \begin{align*} \varphi_* \big( \varphi_{-1}(s) \big) = s, \qquad \text{and} \qquad \varphi_{-1} \big( \varphi_*(s) \big) \leq s. \end{align*} $$
$$ \begin{align*} \varphi_* \big( \varphi_{-1}(s) \big) = s, \qquad \text{and} \qquad \varphi_{-1} \big( \varphi_*(s) \big) \leq s. \end{align*} $$
Clearly, for all
![]() $x>0$
,
$x>0$
,
Let
![]() $u>x_0$
and set
$u>x_0$
and set
By Proposition 4.3,
![]() $\varphi ^* \in \mathrm {WLSC}(\alpha ,c,x_0)$
for some
$\varphi ^* \in \mathrm {WLSC}(\alpha ,c,x_0)$
for some
![]() $c \in (0,1]$
and
$c \in (0,1]$
and
![]() $x_0 \geq 0$
. Thus, for
$x_0 \geq 0$
. Thus, for
![]() $\lambda> c^{-1/\alpha }$
, we get
$\lambda> c^{-1/\alpha }$
, we get
![]() $\varphi ^*(\lambda r_0)> \varphi ^*(r_0)$
. It follows that for all
$\varphi ^*(\lambda r_0)> \varphi ^*(r_0)$
. It follows that for all
![]() $u>x_0$
,
$u>x_0$
,
 $$ \begin{align*} \mathop{\mathrm{sup}}\limits \{ r>0\colon \varphi^*(r)=u \} &\leq \lambda \inf \{ r>0\colon \varphi^*(r)=u \} \\ &\leq \lambda \inf \{ r>0\colon \varphi_*(r)=u \}. \end{align*} $$
$$ \begin{align*} \mathop{\mathrm{sup}}\limits \{ r>0\colon \varphi^*(r)=u \} &\leq \lambda \inf \{ r>0\colon \varphi^*(r)=u \} \\ &\leq \lambda \inf \{ r>0\colon \varphi_*(r)=u \}. \end{align*} $$
Thus, for all
![]() $r>x_0$
,
$r>x_0$
,
 $$ \begin{align*} \varphi^{-1} \big( \varphi^*(r) \big) \lesssim r. \end{align*} $$
$$ \begin{align*} \varphi^{-1} \big( \varphi^*(r) \big) \lesssim r. \end{align*} $$
Corollary 4.5. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
. Then there is
$\alpha>0$
. Then there is
![]() $C> 0$
such that for all
$C> 0$
such that for all
![]() $x> x_0$
,
$x> x_0$
,
 $$ \begin{align} \big(\phi(x) - x \phi'(x) \big) \leq C \varphi(x). \end{align} $$
$$ \begin{align} \big(\phi(x) - x \phi'(x) \big) \leq C \varphi(x). \end{align} $$
Proof. Suppose
![]() $x_0>0$
. We have
$x_0>0$
. We have
 $$ \begin{align*} \big(\phi(x) - x \phi'(x) \big) - \big(\phi(x_0) - x_0 \phi'(x_0^+)\big) = \int_{x_0}^x \varphi(u) \frac{{\textrm{d}} u}{u} = \int_{x_0/x}^1 \varphi(x u) \frac{{\textrm{d}} u}{u}, \end{align*} $$
$$ \begin{align*} \big(\phi(x) - x \phi'(x) \big) - \big(\phi(x_0) - x_0 \phi'(x_0^+)\big) = \int_{x_0}^x \varphi(u) \frac{{\textrm{d}} u}{u} = \int_{x_0/x}^1 \varphi(x u) \frac{{\textrm{d}} u}{u}, \end{align*} $$
where
 $$ \begin{align*} \phi'(x_0^+) = \lim_{x \to x_0^+}\phi'(x). \end{align*} $$
$$ \begin{align*} \phi'(x_0^+) = \lim_{x \to x_0^+}\phi'(x). \end{align*} $$
By the weak lower scaling property of
![]() $\varphi $
, for any
$\varphi $
, for any
![]() $x_0/x < u \leq 1$
, we have
$x_0/x < u \leq 1$
, we have
thus,
 $$ \begin{align*} \big(\phi(x) - x \phi'(x) \big) - \big(\phi(x_0) - x_0 \phi'(x_0^+)\big) \lesssim \varphi(x) \int_0^1 u^{\alpha-1} {\: \rm d} u. \end{align*} $$
$$ \begin{align*} \big(\phi(x) - x \phi'(x) \big) - \big(\phi(x_0) - x_0 \phi'(x_0^+)\big) \lesssim \varphi(x) \int_0^1 u^{\alpha-1} {\: \rm d} u. \end{align*} $$
We denote
![]() $c_1 = \phi (x_0)-x_0 \phi '(x_0^+)$
. Using the scaling property of
$c_1 = \phi (x_0)-x_0 \phi '(x_0^+)$
. Using the scaling property of
![]() $\varphi $
, we conclude that
$\varphi $
, we conclude that
 $$ \begin{align*} c_1 = \frac{c_1}{\varphi(x_0)} \cdot \varphi(x_0) \leq \frac{c_1}{\varphi(x_0)}c^{-1} \bigg( \frac{x_0}{x}\bigg)^{\alpha}\varphi(x) \leq \frac{c_1 c^{-1}}{\varphi(x_0)} \cdot \varphi(x), \end{align*} $$
$$ \begin{align*} c_1 = \frac{c_1}{\varphi(x_0)} \cdot \varphi(x_0) \leq \frac{c_1}{\varphi(x_0)}c^{-1} \bigg( \frac{x_0}{x}\bigg)^{\alpha}\varphi(x) \leq \frac{c_1 c^{-1}}{\varphi(x_0)} \cdot \varphi(x), \end{align*} $$
provided that
![]() $x>x_0$
, which proves (4.12) if
$x>x_0$
, which proves (4.12) if
![]() $x_0>0$
. For
$x_0>0$
. For
![]() $x_0=0$
it is enough to observe that (2.9) implies that
$x_0=0$
it is enough to observe that (2.9) implies that
![]() $\lim _{x \to 0^+}x \phi '(x)=0$
, and the claim follows.
$\lim _{x \to 0^+}x \phi '(x)=0$
, and the claim follows.
Proposition 4.6. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0) \cap \mathrm {WUSC}(\beta -2,C,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0) \cap \mathrm {WUSC}(\beta -2,C,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $C \geq 1$
,
$C \geq 1$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $0 < \alpha \leq \beta < 1$
. Assume also that
$0 < \alpha \leq \beta < 1$
. Assume also that
![]() $b = 0$
. Then for all
$b = 0$
. Then for all
![]() $x> x_0$
,
$x> x_0$
,
and for all
![]() $r>\varphi (x_0)$
,
$r>\varphi (x_0)$
,
Furthermore, there is
![]() $c' \in (0, 1]$
such that for all
$c' \in (0, 1]$
such that for all
![]() $\lambda \geq 1$
and
$\lambda \geq 1$
and
![]() $r> \varphi (x_0)$
,
$r> \varphi (x_0)$
,
 $$ \begin{align} \varphi^{-1}(\lambda r) \geq c' \lambda^{1/\beta} \varphi^{-1}(r). \end{align} $$
$$ \begin{align} \varphi^{-1}(\lambda r) \geq c' \lambda^{1/\beta} \varphi^{-1}(r). \end{align} $$
Proof. Let us observe that, by (2.9), Proposition 2.3 and Proposition 2.4, there is
![]() $c_1 \in (0, 1]$
such that for all
$c_1 \in (0, 1]$
such that for all
![]() $x> x_0$
,
$x> x_0$
,
Now the proof of the lemma is similar to the proof of Proposition 4.3 and is therefore omitted.
4.1. Estimates from above
In this section we show the upper estimates on
![]() $p(t, \: \cdot \:)$
. Before embarking on the proof, let us introduce some notation. Given a set
$p(t, \: \cdot \:)$
. Before embarking on the proof, let us introduce some notation. Given a set
![]() $B \subset \mathbb {R}$
, we define
$B \subset \mathbb {R}$
, we define
 $$ \begin{align*} \delta(B) = \inf\big\{{\lvert {x} \rvert} \colon x \in B \big\} \end{align*} $$
$$ \begin{align*} \delta(B) = \inf\big\{{\lvert {x} \rvert} \colon x \in B \big\} \end{align*} $$
and
 $$ \begin{align*} \operatorname{\mathrm{diam}}(B) = \mathop{\mathrm{sup}}\limits\big\{{\lvert {x-y} \rvert} \colon x, y \in B \big\}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{diam}}(B) = \mathop{\mathrm{sup}}\limits\big\{{\lvert {x-y} \rvert} \colon x, y \in B \big\}. \end{align*} $$
Let
 $$ \begin{align*} b_r = b + \int_{(0, r)} s \: \nu({\textrm{d}} s), \quad r> 0. \end{align*} $$
$$ \begin{align*} b_r = b + \int_{(0, r)} s \: \nu({\textrm{d}} s), \quad r> 0. \end{align*} $$
In view of (2.2), the above definition of
![]() $b_r$
is in line with the usual one (see, e.g., [Reference Kaleta and Sztonyk32, formula (4)] or [Reference Grzywny and Szczypkowski23, formula (1.2)]). Let us define
$b_r$
is in line with the usual one (see, e.g., [Reference Kaleta and Sztonyk32, formula (4)] or [Reference Grzywny and Szczypkowski23, formula (1.2)]). Let us define
![]() $\zeta \colon [0, \infty ) \rightarrow [0, \infty ]$
,
$\zeta \colon [0, \infty ) \rightarrow [0, \infty ]$
,
 $$ \begin{align*} \zeta(s) = \begin{cases} \infty &\quad\text{if } s = 0, \\ \varphi^*(1/s) & \quad \text{if } 0 < s \leq x_0^{-1}, \\ A \phi(1/s) & \quad\text{if } x_0^{-1} < s, \end{cases} \end{align*} $$
$$ \begin{align*} \zeta(s) = \begin{cases} \infty &\quad\text{if } s = 0, \\ \varphi^*(1/s) & \quad \text{if } 0 < s \leq x_0^{-1}, \\ A \phi(1/s) & \quad\text{if } x_0^{-1} < s, \end{cases} \end{align*} $$
where
![]() $A = \varphi ^*(x_0)/\phi (x_0) \in (0, 2]$
.
$A = \varphi ^*(x_0)/\phi (x_0) \in (0, 2]$
.
Theorem 4.7. Let
![]() $\mathbf {T}$
be a subordinator with the Lévy–Khintchine exponent
$\mathbf {T}$
be a subordinator with the Lévy–Khintchine exponent
![]() $\psi $
and the Laplace exponent
$\psi $
and the Laplace exponent
![]() $\phi $
. Suppose that
$\phi $
. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
. Then the probability distribution of
$\alpha>0$
. Then the probability distribution of
![]() $T_t$
has a density
$T_t$
has a density
![]() $p(t, \: \cdot \:)$
. Moreover, there is
$p(t, \: \cdot \:)$
. Moreover, there is
![]() $C> 0$
such that for all
$C> 0$
such that for all
![]() $t \in (0, 1/\varphi (x_0))$
and
$t \in (0, 1/\varphi (x_0))$
and
![]() $x \in \mathbb {R}$
,
$x \in \mathbb {R}$
,
 $$ \begin{align} p\Big(t, x + t b_{1/\psi^{-1}(1/t)}\Big) \leq C \varphi^{-1}(1/t) \cdot \min{\big\{ 1, t \zeta({\lvert {x} \rvert}) \big\}}. \end{align} $$
$$ \begin{align} p\Big(t, x + t b_{1/\psi^{-1}(1/t)}\Big) \leq C \varphi^{-1}(1/t) \cdot \min{\big\{ 1, t \zeta({\lvert {x} \rvert}) \big\}}. \end{align} $$
In particular, for all
![]() $t \in (0, 1/\varphi (x_0))$
and
$t \in (0, 1/\varphi (x_0))$
and
![]() $x \geq 2e t\phi '(\psi ^{-1}(1/t))$
,
$x \geq 2e t\phi '(\psi ^{-1}(1/t))$
,
 $$ \begin{align} p(t,x + t b) \leq C \varphi^{-1}(1/t) \cdot \min{\big\{ 1, t\zeta(x) \big\}}. \end{align} $$
$$ \begin{align} p(t,x + t b) \leq C \varphi^{-1}(1/t) \cdot \min{\big\{ 1, t\zeta(x) \big\}}. \end{align} $$
Proof. Without loss of generality, we can assume
![]() $b = 0$
. Indeed, otherwise it is enough to consider a shifted process
$b = 0$
. Indeed, otherwise it is enough to consider a shifted process
![]() $\widetilde {T_t} = T_t - tb$
. Next, let us observe that for any Borel set
$\widetilde {T_t} = T_t - tb$
. Next, let us observe that for any Borel set
![]() $B \subset \mathbb {R}$
, we have
$B \subset \mathbb {R}$
, we have
 $$ \begin{align} \nonumber \nu(B) & \lesssim \int_{(\delta(B), \infty)} \big(1 - e^{-s/\delta(B)}\big) \: \nu({\textrm{d}} s) \\ &\leq \phi\big(1/\delta(B)\big). \end{align} $$
$$ \begin{align} \nonumber \nu(B) & \lesssim \int_{(\delta(B), \infty)} \big(1 - e^{-s/\delta(B)}\big) \: \nu({\textrm{d}} s) \\ &\leq \phi\big(1/\delta(B)\big). \end{align} $$
Furthermore, for
![]() $\delta (B)<1/x_0$
, by Proposition 4.1 and Remark 3.2,
$\delta (B)<1/x_0$
, by Proposition 4.1 and Remark 3.2,
 $$ \begin{align*} \nu(B) &\leq h(\delta(B)) \\ &\lesssim \varphi^*(1/\delta(B)). \end{align*} $$
$$ \begin{align*} \nu(B) &\leq h(\delta(B)) \\ &\lesssim \varphi^*(1/\delta(B)). \end{align*} $$
Thus,
![]() $\nu (B) \lesssim \zeta (\delta (B))$
. We claim that
$\nu (B) \lesssim \zeta (\delta (B))$
. We claim that
![]() $\zeta $
has doubling property on
$\zeta $
has doubling property on
![]() $(0, \infty )$
. Indeed, since
$(0, \infty )$
. Indeed, since
![]() $-\phi ^{\prime \prime }$
is nonincreasing function with the weak lower scaling property, it has doubling property on
$-\phi ^{\prime \prime }$
is nonincreasing function with the weak lower scaling property, it has doubling property on
![]() $(x_0, \infty )$
; thus, for
$(x_0, \infty )$
; thus, for
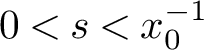 $0 < s < x_0^{-1}$
,
$0 < s < x_0^{-1}$
,
 $$ \begin{align*} \zeta\big(\tfrac{1}{2} s\big) \approx 4 s^{-2} (-\phi^{\prime\prime}(2/s)) \lesssim s^{-2} (-\phi^{\prime\prime}(1/s)) \lesssim \zeta(s). \end{align*} $$
$$ \begin{align*} \zeta\big(\tfrac{1}{2} s\big) \approx 4 s^{-2} (-\phi^{\prime\prime}(2/s)) \lesssim s^{-2} (-\phi^{\prime\prime}(1/s)) \lesssim \zeta(s). \end{align*} $$
This completes the argument in the case
![]() $x_0 = 0$
. If
$x_0 = 0$
. If
![]() $x_0> 0$
, then by (2.10), for
$x_0> 0$
, then by (2.10), for
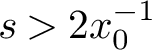 $s> 2 x_0^{-1}$
we have
$s> 2 x_0^{-1}$
we have
 $$ \begin{align*} \zeta\big(\tfrac{1}{2} s\big) = A \phi(2/s) \leq 2 A \phi(1/s) \leq 2 \zeta(s). \end{align*} $$
$$ \begin{align*} \zeta\big(\tfrac{1}{2} s\big) = A \phi(2/s) \leq 2 A \phi(1/s) \leq 2 \zeta(s). \end{align*} $$
Lastly, the function
 $$ \begin{align*} \big[\tfrac{1}{2} x_0, x_0] \ni x \mapsto \frac{\varphi^*(2 x)}{\phi(x)} \end{align*} $$
$$ \begin{align*} \big[\tfrac{1}{2} x_0, x_0] \ni x \mapsto \frac{\varphi^*(2 x)}{\phi(x)} \end{align*} $$
is continuous and thus it is bounded.
Next, for
![]() $s> 0$
and
$s> 0$
and
![]() $x \in \mathbb {R}$
,
$x \in \mathbb {R}$
,
 $$ \begin{align*} s \vee {\lvert {x} \rvert} - \tfrac{1}{2} {\lvert {x} \rvert} \geq \tfrac{1}{2} s; \end{align*} $$
$$ \begin{align*} s \vee {\lvert {x} \rvert} - \tfrac{1}{2} {\lvert {x} \rvert} \geq \tfrac{1}{2} s; \end{align*} $$
thus, by motonicity and the doubling property of
![]() $\zeta $
, we get
$\zeta $
, we get
 $$ \begin{align*} \zeta\big(s \vee {\lvert {x} \rvert} - \tfrac{1}{2} {\lvert {x} \rvert} \big) \lesssim \zeta(s). \end{align*} $$
$$ \begin{align*} \zeta\big(s \vee {\lvert {x} \rvert} - \tfrac{1}{2} {\lvert {x} \rvert} \big) \lesssim \zeta(s). \end{align*} $$
Hence, by (2.4) and (4.2), for
![]() $r> 0$
,
$r> 0$
,
 $$ \begin{align} \nonumber \int_{(r, \infty)} \zeta\big(s \vee x - \tfrac{1}{2} x \big) \: \nu({\textrm{d}} x) &\lesssim \zeta(s) h(r) \\ &\lesssim \zeta(s) \psi^*(1/r). \end{align} $$
$$ \begin{align} \nonumber \int_{(r, \infty)} \zeta\big(s \vee x - \tfrac{1}{2} x \big) \: \nu({\textrm{d}} x) &\lesssim \zeta(s) h(r) \\ &\lesssim \zeta(s) \psi^*(1/r). \end{align} $$
Since
![]() $\psi ^*$
has the weak lower scaling property and satisfies (4.3), by [Reference Grzywny and Szczypkowski23, Proposition 3.4] together with Proposition 4.2, there are
$\psi ^*$
has the weak lower scaling property and satisfies (4.3), by [Reference Grzywny and Szczypkowski23, Proposition 3.4] together with Proposition 4.2, there are
![]() $C> 0$
and
$C> 0$
and
![]() $t_1 \in (0, \infty ]$
such that for all
$t_1 \in (0, \infty ]$
such that for all
![]() $t \in (0, t_1)$
,
$t \in (0, t_1)$
,
 $$ \begin{align} \int_{\mathbb{R}} e^{-t \Re \psi(\xi)} {\lvert {\xi} \rvert} {\: \rm d} \xi \leq C \big(\psi^{-1}(1/t)\big)^2. \end{align} $$
$$ \begin{align} \int_{\mathbb{R}} e^{-t \Re \psi(\xi)} {\lvert {\xi} \rvert} {\: \rm d} \xi \leq C \big(\psi^{-1}(1/t)\big)^2. \end{align} $$
If
![]() $x_0 = 0$
, then
$x_0 = 0$
, then
![]() $t_1 = \infty $
. If
$t_1 = \infty $
. If
![]() $t_1 < 1/\varphi (x_0)$
, we can expand the above estimate for
$t_1 < 1/\varphi (x_0)$
, we can expand the above estimate for
![]() $t_1\leq t< 1/\varphi (x_0)$
using positivity of the right-hand side and monotonicity of the left-hand side.
$t_1\leq t< 1/\varphi (x_0)$
using positivity of the right-hand side and monotonicity of the left-hand side.
In view of (4.19), (4.20) and (4.21), by [Reference Kaleta and Sztonyk32, Theorem 1] with
![]() $\gamma =\,0$
, there are
$\gamma =\,0$
, there are
![]() $C_1,C_2,C_3> 0$
such that for all
$C_1,C_2,C_3> 0$
such that for all
![]() $t \in (0 , 1/\varphi (x_0))$
and
$t \in (0 , 1/\varphi (x_0))$
and
![]() $x \in \mathbb {R}$
,
$x \in \mathbb {R}$
,
 $$ \begin{align*} & p\Big(t, x+t b_{1/\psi^{-1}(1/t)} \Big) \\ &\quad\leq C_1 \psi^{-1}(1/t) \cdot \min{ \bigg\{ 1, t \zeta\big(\tfrac{1}{4} {\lvert {x} \rvert} \big) + \exp\Big\{-C_2 {\lvert {x} \rvert} \psi^{-1}(1/t) \log \big(1 + C_3 {\lvert {x} \rvert} \psi^{-1}(1/t)\big) \Big\} \bigg\}}. \end{align*} $$
$$ \begin{align*} & p\Big(t, x+t b_{1/\psi^{-1}(1/t)} \Big) \\ &\quad\leq C_1 \psi^{-1}(1/t) \cdot \min{ \bigg\{ 1, t \zeta\big(\tfrac{1}{4} {\lvert {x} \rvert} \big) + \exp\Big\{-C_2 {\lvert {x} \rvert} \psi^{-1}(1/t) \log \big(1 + C_3 {\lvert {x} \rvert} \psi^{-1}(1/t)\big) \Big\} \bigg\}}. \end{align*} $$
Let us consider
![]() $x> 0$
and
$x> 0$
and
![]() $t \in (0, 1/\varphi (x_0))$
such that
$t \in (0, 1/\varphi (x_0))$
such that
![]() $t \zeta (x) \leq 1$
. We claim that
$t \zeta (x) \leq 1$
. We claim that
 $$ \begin{align} \exp\Big\{-C_2 x \psi^{-1}(1/t) \log\big(1 + C_3 x \psi^{-1}(1/t)\big)\Big\} \lesssim t \zeta(x). \end{align} $$
$$ \begin{align} \exp\Big\{-C_2 x \psi^{-1}(1/t) \log\big(1 + C_3 x \psi^{-1}(1/t)\big)\Big\} \lesssim t \zeta(x). \end{align} $$
First suppose that
 $x>x_0^{-1}$
. Let us observe that the function
$x>x_0^{-1}$
. Let us observe that the function
 $$ \begin{align*} [0, \infty) \ni u \mapsto u \exp\Big\{-C_2 u \log \big(1+C_3 u\big) \Big\} \end{align*} $$
$$ \begin{align*} [0, \infty) \ni u \mapsto u \exp\Big\{-C_2 u \log \big(1+C_3 u\big) \Big\} \end{align*} $$
is bounded. Therefore,
 $$ \begin{align} \exp\Big\{-C_2 x \psi^{-1}(1/t) \log\big(1 + C_3 x \psi^{-1}(1/t)\big)\Big\} \lesssim \frac{1}{x \psi^{-1}(1/t)}. \end{align} $$
$$ \begin{align} \exp\Big\{-C_2 x \psi^{-1}(1/t) \log\big(1 + C_3 x \psi^{-1}(1/t)\big)\Big\} \lesssim \frac{1}{x \psi^{-1}(1/t)}. \end{align} $$
Since
![]() $x \phi ^{-1}(1/t) \geq 1$
, by (2.10), we have
$x \phi ^{-1}(1/t) \geq 1$
, by (2.10), we have
 $$ \begin{align} t \phi(1/x) = \frac{\phi(1/x)}{\phi\big(x \phi^{-1}(1/t) \cdot 1/x\big)} \geq \frac{1}{x \phi^{-1}(1/t)}. \end{align} $$
$$ \begin{align} t \phi(1/x) = \frac{\phi(1/x)}{\phi\big(x \phi^{-1}(1/t) \cdot 1/x\big)} \geq \frac{1}{x \phi^{-1}(1/t)}. \end{align} $$
Next, in light of (2.9), for all
![]() $y> 0$
,
$y> 0$
,
 $$ \begin{align*} \tfrac{1}{2} \varphi^*(y) \leq \phi(y); \end{align*} $$
$$ \begin{align*} \tfrac{1}{2} \varphi^*(y) \leq \phi(y); \end{align*} $$
hence, by the monotonicity of
![]() $\phi ^{-1}$
,
$\phi ^{-1}$
,
 $$ \begin{align} \nonumber \phi^{-1}(1/t) &= \phi^{-1}\big(\tfrac{1}{2} \varphi^*(\varphi^{-1}(2/t))\big) \\ \nonumber &\leq \phi^{-1}\big(\phi(\varphi^{-1}(2/t))\big) \\ \nonumber &= \varphi^{-1}(2/t) \\ &\leq C \psi^{-1}(1/t), \end{align} $$
$$ \begin{align} \nonumber \phi^{-1}(1/t) &= \phi^{-1}\big(\tfrac{1}{2} \varphi^*(\varphi^{-1}(2/t))\big) \\ \nonumber &\leq \phi^{-1}\big(\phi(\varphi^{-1}(2/t))\big) \\ \nonumber &= \varphi^{-1}(2/t) \\ &\leq C \psi^{-1}(1/t), \end{align} $$
where in the last step we have used Proposition 4.3. Putting (4.23), (4.24) and (4.25) together, we obtain (4.22) as claimed.
Now let
 $0<x \leq x_0^{-1}$
. Observe that the function
$0<x \leq x_0^{-1}$
. Observe that the function
 $$ \begin{align*} [0, \infty) \ni u \mapsto u^2 \exp\Big\{-C_2 u \log \big(1+C_3 u\big) \Big\} \end{align*} $$
$$ \begin{align*} [0, \infty) \ni u \mapsto u^2 \exp\Big\{-C_2 u \log \big(1+C_3 u\big) \Big\} \end{align*} $$
is also bounded. Hence,
 $$ \begin{align} \exp\Big\{-C_2 x \psi^{-1}(1/t) \log\big(1 + C_3 x \psi^{-1}(1/t)\big)\Big\} \lesssim \frac{1}{\big(x \psi^{-1}(1/t)\big)^2}. \end{align} $$
$$ \begin{align} \exp\Big\{-C_2 x \psi^{-1}(1/t) \log\big(1 + C_3 x \psi^{-1}(1/t)\big)\Big\} \lesssim \frac{1}{\big(x \psi^{-1}(1/t)\big)^2}. \end{align} $$
Since
![]() $x \varphi ^{-1}(1/t) \geq 1$
, using (4.5) we get
$x \varphi ^{-1}(1/t) \geq 1$
, using (4.5) we get
 $$ \begin{align} t\varphi^*(1/x) = \frac{\varphi^*(1/x)}{\varphi^*\big( x\varphi^{-1}(1/t) \cdot 1/x \big)} \geq \frac{1}{\big( x\varphi^{-1}(1/t) \big)^2}. \end{align} $$
$$ \begin{align} t\varphi^*(1/x) = \frac{\varphi^*(1/x)}{\varphi^*\big( x\varphi^{-1}(1/t) \cdot 1/x \big)} \geq \frac{1}{\big( x\varphi^{-1}(1/t) \big)^2}. \end{align} $$
Hence, putting together (4.26) and (4.27) and invoking Proposition 4.2, we again obtain (4.22).
Finally, using doubling property of
![]() $\zeta $
we get
$\zeta $
we get
 $$ \begin{align*} \zeta\big(\tfrac{1}{4} x\big) \lesssim \zeta(x); \end{align*} $$
$$ \begin{align*} \zeta\big(\tfrac{1}{4} x\big) \lesssim \zeta(x); \end{align*} $$
thus, another application of Proposition 4.3 leads to (4.17).
For the proof of (4.18), we observe that
 $$ \begin{align*} \phi'(\lambda) = \int_{(0, \infty)} x e^{-\lambda x} \: \nu({\textrm{d}} x) \geq e^{-1} \int_{(0, 1/\lambda)} x \: \nu({\textrm{d}} x). \end{align*} $$
$$ \begin{align*} \phi'(\lambda) = \int_{(0, \infty)} x e^{-\lambda x} \: \nu({\textrm{d}} x) \geq e^{-1} \int_{(0, 1/\lambda)} x \: \nu({\textrm{d}} x). \end{align*} $$
Thus,
 $$ \begin{align*} b_{1/\psi^{-1}(1/t)} = \int_{(0, 1/\psi^{-1}(1/t))} x \: \nu({\textrm{d}}x) \leq e \phi'(\psi^{-1}(1/t)). \end{align*} $$
$$ \begin{align*} b_{1/\psi^{-1}(1/t)} = \int_{(0, 1/\psi^{-1}(1/t))} x \: \nu({\textrm{d}}x) \leq e \phi'(\psi^{-1}(1/t)). \end{align*} $$
Hence, by monotonicity and the doubling property of
![]() $\zeta $
, for
$\zeta $
, for
![]() $x> 2e t \phi '(\psi ^{-1}(1/t))$
, we obtain
$x> 2e t \phi '(\psi ^{-1}(1/t))$
, we obtain
 $$ \begin{align*} \zeta\Big(x - t b_{1/\psi^{-1}(1/t)}\Big) \leq \zeta\bigg(\frac{x}{2}\bigg) \lesssim \zeta (x), \end{align*} $$
$$ \begin{align*} \zeta\Big(x - t b_{1/\psi^{-1}(1/t)}\Big) \leq \zeta\bigg(\frac{x}{2}\bigg) \lesssim \zeta (x), \end{align*} $$
and the theorem follows.
Now we define
![]() $\eta \colon [0, \infty ) \rightarrow [0, \infty ]$
,
$\eta \colon [0, \infty ) \rightarrow [0, \infty ]$
,
 $$ \begin{align*} \eta(s) = s^{-1}\zeta(s)= \begin{cases} \infty &\quad\text{if } s = 0, \\ s^{-1} \varphi^*(1/s) & \quad\text{if } 0 < s \leq x_0^{-1}, \\ A s^{-1} \phi(1/s) &\quad \text{if } x_0^{-1} < s, \end{cases} \end{align*} $$
$$ \begin{align*} \eta(s) = s^{-1}\zeta(s)= \begin{cases} \infty &\quad\text{if } s = 0, \\ s^{-1} \varphi^*(1/s) & \quad\text{if } 0 < s \leq x_0^{-1}, \\ A s^{-1} \phi(1/s) &\quad \text{if } x_0^{-1} < s, \end{cases} \end{align*} $$
where
![]() $A = \varphi ^*(x_0)/\phi (x_0) \in (0, 2]$
. Notice that, by (2.9), if
$A = \varphi ^*(x_0)/\phi (x_0) \in (0, 2]$
. Notice that, by (2.9), if
![]() $2 t \zeta ({\lvert {x} \rvert }) \leq 1$
, then
$2 t \zeta ({\lvert {x} \rvert }) \leq 1$
, then
![]() $t \varphi ^*(1/{\lvert {x} \rvert }) \leq 1$
, and so
$t \varphi ^*(1/{\lvert {x} \rvert }) \leq 1$
, and so
 $$ \begin{align*} \eta({\lvert {x} \rvert}) &= {\lvert {x} \rvert}^{-1} \zeta({\lvert {x} \rvert}) \\ & \leq \varphi^{-1}(1/t) \zeta({\lvert {x} \rvert}). \end{align*} $$
$$ \begin{align*} \eta({\lvert {x} \rvert}) &= {\lvert {x} \rvert}^{-1} \zeta({\lvert {x} \rvert}) \\ & \leq \varphi^{-1}(1/t) \zeta({\lvert {x} \rvert}). \end{align*} $$
Therefore,
 $$ \begin{align*} \min{\big\{\varphi^{-1}(1/t), t \eta({\lvert {x} \rvert}) \big\}} \leq 4 \varphi^{-1}(1/t) \cdot \min{\big\{1, t \zeta({\lvert {x} \rvert}) \big\}}. \end{align*} $$
$$ \begin{align*} \min{\big\{\varphi^{-1}(1/t), t \eta({\lvert {x} \rvert}) \big\}} \leq 4 \varphi^{-1}(1/t) \cdot \min{\big\{1, t \zeta({\lvert {x} \rvert}) \big\}}. \end{align*} $$
Theorem 4.8. Let
![]() $\mathbf {T}$
be a subordinator with the Lévy–Khintchine exponent
$\mathbf {T}$
be a subordinator with the Lévy–Khintchine exponent
![]() $\psi $
and the Laplace exponent
$\psi $
and the Laplace exponent
![]() $\phi $
. Suppose that
$\phi $
. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0,1]$
,
$c \in (0,1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
. We also assume that the Lévy measure
$\alpha>0$
. We also assume that the Lévy measure
![]() $\nu $
has an almost monotone density
$\nu $
has an almost monotone density
![]() $\nu (x)$
. Then the probability distribution of
$\nu (x)$
. Then the probability distribution of
![]() $T_t$
has a density
$T_t$
has a density
![]() $p(t, \: \cdot \:)$
. Moreover, there is
$p(t, \: \cdot \:)$
. Moreover, there is
![]() $C> 0$
such that for all
$C> 0$
such that for all
![]() $t\in (0,1/\varphi (x_0))$
and
$t\in (0,1/\varphi (x_0))$
and
![]() $x \in \mathbb {R}$
,
$x \in \mathbb {R}$
,
 $$ \begin{align} p\Big(t,x+t b_{1/\psi^{-1}(1/t)}\Big) \leq C \min{\big\{\varphi^{-1}(1/t), t \eta({\lvert {x} \rvert}) \big\}}. \end{align} $$
$$ \begin{align} p\Big(t,x+t b_{1/\psi^{-1}(1/t)}\Big) \leq C \min{\big\{\varphi^{-1}(1/t), t \eta({\lvert {x} \rvert}) \big\}}. \end{align} $$
In particular, for all
![]() $t \in (0, 1/\varphi (x_0))$
and
$t \in (0, 1/\varphi (x_0))$
and
![]() $x \geq 2e t\phi '(\psi ^{-1}(1/t))$
,
$x \geq 2e t\phi '(\psi ^{-1}(1/t))$
,
 $$ \begin{align} p(t, x + t b) \leq C \min{\big\{\varphi^{-1}(1/t), t \eta(x) \big\}}. \end{align} $$
$$ \begin{align} p(t, x + t b) \leq C \min{\big\{\varphi^{-1}(1/t), t \eta(x) \big\}}. \end{align} $$
Proof. Without loss of generality, we can assume
![]() $b = 0$
. Let us observe that for any
$b = 0$
. Let us observe that for any
![]() $\lambda> 0$
,
$\lambda> 0$
,
 $$ \begin{align*} \phi(\lambda) \geq \int_0^{1/\lambda} \big(1 - e^{-\lambda s} \big) \nu(s) {\: \rm d} s \gtrsim \nu(1/\lambda) \lambda^{-1} \end{align*} $$
$$ \begin{align*} \phi(\lambda) \geq \int_0^{1/\lambda} \big(1 - e^{-\lambda s} \big) \nu(s) {\: \rm d} s \gtrsim \nu(1/\lambda) \lambda^{-1} \end{align*} $$
and
 $$ \begin{align*} -\phi^{\prime\prime}(\lambda) \geq \int_0^{1/\lambda} s^2 e^{-\lambda s} \nu(s) {\: \rm d} s \gtrsim \nu(1/\lambda) \lambda^{-3}. \end{align*} $$
$$ \begin{align*} -\phi^{\prime\prime}(\lambda) \geq \int_0^{1/\lambda} s^2 e^{-\lambda s} \nu(s) {\: \rm d} s \gtrsim \nu(1/\lambda) \lambda^{-3}. \end{align*} $$
Hence,
Since
![]() $\eta $
is nonincreasing, for any Borel subset
$\eta $
is nonincreasing, for any Borel subset
![]() $B \subset \mathbb {R}$
,
$B \subset \mathbb {R}$
,
 $$ \begin{align} \nu(B) &\lesssim \int_{B \cap (0,\infty)} \eta(x) {\: \rm d} x \lesssim \eta\big(\delta(B)\big) \operatorname{\mathrm{diam}}(B). \end{align} $$
$$ \begin{align} \nu(B) &\lesssim \int_{B \cap (0,\infty)} \eta(x) {\: \rm d} x \lesssim \eta\big(\delta(B)\big) \operatorname{\mathrm{diam}}(B). \end{align} $$
Arguing as in the proof of Theorem 4.7, we conclude that
![]() $\eta $
has a doubling property on
$\eta $
has a doubling property on
![]() $(0,\infty )$
. Using that and monotonicity of
$(0,\infty )$
. Using that and monotonicity of
![]() $\eta $
, for
$\eta $
, for
![]() $s> 0$
and
$s> 0$
and
![]() $x \in \mathbb {R}$
,
$x \in \mathbb {R}$
,
 $$ \begin{align*} \eta\big(s \vee x - \tfrac{1}{2} x\big) \leq \eta\big(\tfrac{1}{2} s \big) \lesssim \eta(s). \end{align*} $$
$$ \begin{align*} \eta\big(s \vee x - \tfrac{1}{2} x\big) \leq \eta\big(\tfrac{1}{2} s \big) \lesssim \eta(s). \end{align*} $$
Therefore, by (4.2), for
![]() $r> 0$
,
$r> 0$
,
 $$ \begin{align} \int_r^\infty \eta\big(s \vee x - \tfrac{1}{2} x\big) \nu(x) {\: \rm d} x \lesssim \eta(s) \psi^*(1/r). \end{align} $$
$$ \begin{align} \int_r^\infty \eta\big(s \vee x - \tfrac{1}{2} x\big) \nu(x) {\: \rm d} x \lesssim \eta(s) \psi^*(1/r). \end{align} $$
Since
![]() $\psi ^*$
has the weak lower scaling property and satisfies (4.3), by [Reference Grzywny and Szczypkowski23, Theorem 3.1] and Proposition 4.2, there are
$\psi ^*$
has the weak lower scaling property and satisfies (4.3), by [Reference Grzywny and Szczypkowski23, Theorem 3.1] and Proposition 4.2, there are
![]() $C> 0$
and
$C> 0$
and
![]() $t_1 \in (0, \infty ]$
such that for all
$t_1 \in (0, \infty ]$
such that for all
![]() $t \in (0, t_1)$
,
$t \in (0, t_1)$
,
 $$ \begin{align} \int_{\mathbb{R}} e^{-t\Re \psi(\xi)} {\: \rm d} \xi \leq C \psi^{-1}(1/t). \end{align} $$
$$ \begin{align} \int_{\mathbb{R}} e^{-t\Re \psi(\xi)} {\: \rm d} \xi \leq C \psi^{-1}(1/t). \end{align} $$
If
![]() $x_0 = 0$
, then
$x_0 = 0$
, then
![]() $t_1 = \infty $
. If
$t_1 = \infty $
. If
![]() $t_1 < 48/\varphi (x_0)$
, we can expand the above estimate for
$t_1 < 48/\varphi (x_0)$
, we can expand the above estimate for
![]() $t_1\leq t< 48/\varphi (x_0)$
using positivity of the right-hand side and monotonicity of the left-hand side.
$t_1\leq t< 48/\varphi (x_0)$
using positivity of the right-hand side and monotonicity of the left-hand side.
In view of (4.31), (4.32) and (4.33), by [Reference Grzywny and Szczypkowski22, Theorem 2.1], there is
![]() $C> 0$
such that for all
$C> 0$
such that for all
![]() $t \in (0, 1/\varphi (x_0))$
and
$t \in (0, 1/\varphi (x_0))$
and
![]() $x \in \mathbb {R}$
,
$x \in \mathbb {R}$
,
 $$ \begin{align*} p\Big(t,x+tb_{1/\psi^{-1}(1/t)}\Big) \leq C \psi^{-1}(1/t) \cdot \min{ \Big\{ 1, t \big(\psi^{-1}(1/t)\big)^{-1} \eta({\lvert {x} \rvert})+\big(1+{\lvert {x} \rvert}\psi^{-1}(1/t)\big)^{-3} \Big\}}. \end{align*} $$
$$ \begin{align*} p\Big(t,x+tb_{1/\psi^{-1}(1/t)}\Big) \leq C \psi^{-1}(1/t) \cdot \min{ \Big\{ 1, t \big(\psi^{-1}(1/t)\big)^{-1} \eta({\lvert {x} \rvert})+\big(1+{\lvert {x} \rvert}\psi^{-1}(1/t)\big)^{-3} \Big\}}. \end{align*} $$
We claim that
 $$ \begin{align} \frac{\psi^{-1}(1/t)}{\big(1+{\lvert {x} \rvert}\psi^{-1}(1/t)\big)^3} \lesssim t \eta({\lvert {x} \rvert}) \end{align} $$
$$ \begin{align} \frac{\psi^{-1}(1/t)}{\big(1+{\lvert {x} \rvert}\psi^{-1}(1/t)\big)^3} \lesssim t \eta({\lvert {x} \rvert}) \end{align} $$
whenever
 $t \eta ({\lvert {x} \rvert }) \leq \tfrac {A}{2} \varphi ^{-1}(1/t)$
.
$t \eta ({\lvert {x} \rvert }) \leq \tfrac {A}{2} \varphi ^{-1}(1/t)$
.
First, let us show that for any
![]() $\epsilon \in (0, 1]$
, the condition
$\epsilon \in (0, 1]$
, the condition
 $t \eta ({\lvert {x} \rvert }) \leq \tfrac {A \epsilon }{2} \varphi ^{-1}(1/t)$
implies that
$t \eta ({\lvert {x} \rvert }) \leq \tfrac {A \epsilon }{2} \varphi ^{-1}(1/t)$
implies that
 $$ \begin{align} t \varphi^*\bigg(\frac{1}{{\lvert {x} \rvert}}\bigg) \leq \epsilon {\lvert {x} \rvert} \varphi^{-1}\bigg(\frac{1}{t}\bigg). \end{align} $$
$$ \begin{align} t \varphi^*\bigg(\frac{1}{{\lvert {x} \rvert}}\bigg) \leq \epsilon {\lvert {x} \rvert} \varphi^{-1}\bigg(\frac{1}{t}\bigg). \end{align} $$
Indeed, by (2.9), we have
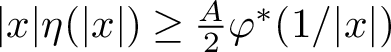 ${\lvert {x} \rvert } \eta ({\lvert {x} \rvert }) \geq \tfrac {A}{2} \varphi ^*(1/{\lvert {x} \rvert })$
; thus,
${\lvert {x} \rvert } \eta ({\lvert {x} \rvert }) \geq \tfrac {A}{2} \varphi ^*(1/{\lvert {x} \rvert })$
; thus,
 $$ \begin{align*} \epsilon {\lvert {x} \rvert} \varphi^{-1}\left(\frac{1}{t}\right) \geq \frac{2}{A} t {\lvert {x} \rvert} \eta({\lvert {x} \rvert}) \geq t \varphi^*\left(\frac{1}{{\lvert {x} \rvert}}\right). \end{align*} $$
$$ \begin{align*} \epsilon {\lvert {x} \rvert} \varphi^{-1}\left(\frac{1}{t}\right) \geq \frac{2}{A} t {\lvert {x} \rvert} \eta({\lvert {x} \rvert}) \geq t \varphi^*\left(\frac{1}{{\lvert {x} \rvert}}\right). \end{align*} $$
Notice also that
![]() $\epsilon ^{1/3} {\lvert {x} \rvert } \varphi ^{-1}(1/t) \geq 1$
since otherwise, by (4.5),
$\epsilon ^{1/3} {\lvert {x} \rvert } \varphi ^{-1}(1/t) \geq 1$
since otherwise, by (4.5),
 $$ \begin{align*} 1 < t \varphi^*\bigg(\frac{1}{\epsilon^{1/3} {\lvert {x} \rvert}}\bigg) < \frac{1}{\epsilon^{2/3}} t \varphi^*\bigg(\frac{1}{{\lvert {x} \rvert}}\bigg), \end{align*} $$
$$ \begin{align*} 1 < t \varphi^*\bigg(\frac{1}{\epsilon^{1/3} {\lvert {x} \rvert}}\bigg) < \frac{1}{\epsilon^{2/3}} t \varphi^*\bigg(\frac{1}{{\lvert {x} \rvert}}\bigg), \end{align*} $$
which entails that
![]() $\epsilon ^{2/3} < t \varphi ^*(1/{\lvert {x} \rvert })$
; that is,
$\epsilon ^{2/3} < t \varphi ^*(1/{\lvert {x} \rvert })$
; that is,
![]() $\epsilon ^{1/3} {\lvert {x} \rvert } \varphi ^{-1}(1/t) < \epsilon ^{-2/3} t \varphi ^*(1/{\lvert {x} \rvert })$
, contrary to (4.35).
$\epsilon ^{1/3} {\lvert {x} \rvert } \varphi ^{-1}(1/t) < \epsilon ^{-2/3} t \varphi ^*(1/{\lvert {x} \rvert })$
, contrary to (4.35).
To show (4.34), let us suppose that
 $t \eta ({\lvert {x} \rvert }) \leq \tfrac {A}{2} \varphi ^{-1}(1/t)$
; thus,
$t \eta ({\lvert {x} \rvert }) \leq \tfrac {A}{2} \varphi ^{-1}(1/t)$
; thus,
![]() ${\lvert {x} \rvert } \varphi ^{-1}(1/t) \geq 1$
. By (4.5), we have
${\lvert {x} \rvert } \varphi ^{-1}(1/t) \geq 1$
. By (4.5), we have
 $$ \begin{align*} t \varphi^*(1/{\lvert {x} \rvert}) = \frac{\varphi^*(1/{\lvert {x} \rvert})}{\varphi^*\big({\lvert {x} \rvert} \varphi^{-1}(1/t) \cdot 1/{\lvert {x} \rvert}\big)} \geq \frac{1}{({\lvert {x} \rvert} \varphi^{-1}(1/t))^2}, \end{align*} $$
$$ \begin{align*} t \varphi^*(1/{\lvert {x} \rvert}) = \frac{\varphi^*(1/{\lvert {x} \rvert})}{\varphi^*\big({\lvert {x} \rvert} \varphi^{-1}(1/t) \cdot 1/{\lvert {x} \rvert}\big)} \geq \frac{1}{({\lvert {x} \rvert} \varphi^{-1}(1/t))^2}, \end{align*} $$
which, by Proposition 4.3, gives
 $$ \begin{align*} t {\lvert {x} \rvert} \eta({\lvert {x} \rvert}) \geq \tfrac{A}{2} t \varphi^*(1/{\lvert {x} \rvert}) \gtrsim \frac{|x|\psi^{-1}(1/t)}{(1 + {\lvert {x} \rvert} \psi^{-1}(1/t))^3}, \end{align*} $$
$$ \begin{align*} t {\lvert {x} \rvert} \eta({\lvert {x} \rvert}) \geq \tfrac{A}{2} t \varphi^*(1/{\lvert {x} \rvert}) \gtrsim \frac{|x|\psi^{-1}(1/t)}{(1 + {\lvert {x} \rvert} \psi^{-1}(1/t))^3}, \end{align*} $$
proving (4.34), and (4.28) follows. The inequality (4.29) holds by the same argument as in the proof of Theorem 4.7.
Remark 4.9. In statements of Theorems 4.7 and 4.8, we can replace
![]() $b_{1/\psi ^{-1}(1/t)}$
by
$b_{1/\psi ^{-1}(1/t)}$
by
![]() $b_{1/\varphi ^{-1}(1/t)}$
. Indeed, let us observe that if
$b_{1/\varphi ^{-1}(1/t)}$
. Indeed, let us observe that if
![]() $0 < r_1 \leq r_2 < 1/x_0$
, then
$0 < r_1 \leq r_2 < 1/x_0$
, then
 $$ \begin{align} \nonumber \big| b_{r_1} - b_{r_2} \big| &\leq \int_{(r_1, r_2]} s \: \nu({\textrm{d}} s) \\ \nonumber &\leq r_1^{-1} r_2^2 h(r_2) \\ &\lesssim r_1^{-1} r_2^2 \psi^*(1/r_2), \end{align} $$
$$ \begin{align} \nonumber \big| b_{r_1} - b_{r_2} \big| &\leq \int_{(r_1, r_2]} s \: \nu({\textrm{d}} s) \\ \nonumber &\leq r_1^{-1} r_2^2 h(r_2) \\ &\lesssim r_1^{-1} r_2^2 \psi^*(1/r_2), \end{align} $$
where in the last estimate we have used (4.2). Hence, by (4.9), we get
 $$ \begin{align} \big| b_{r_1} - b_{r_2} \big| \lesssim r_1^{-1} r_2^2 \varphi^*(1/r_2). \end{align} $$
$$ \begin{align} \big| b_{r_1} - b_{r_2} \big| \lesssim r_1^{-1} r_2^2 \varphi^*(1/r_2). \end{align} $$
Therefore, by (4.36), (4.37) and Proposition 4.3, there is
![]() $C \geq 1$
such that
$C \geq 1$
such that
 $$ \begin{align} \Big| b_{1/\psi^{-1}(1/t)} - b_{1/\varphi^{-1}(1/t)} \Big| \leq C \frac{1}{t \varphi^{-1}(1/t)}, \end{align} $$
$$ \begin{align} \Big| b_{1/\psi^{-1}(1/t)} - b_{1/\varphi^{-1}(1/t)} \Big| \leq C \frac{1}{t \varphi^{-1}(1/t)}, \end{align} $$
provided that
![]() $0 < t < 1/\varphi (x_0)$
. Now, let us suppose that
$0 < t < 1/\varphi (x_0)$
. Now, let us suppose that
 $8 C^2 t \zeta \big ({\lvert {x} \rvert }\big ) \leq 1$
. Then, by (2.10) and (4.5),
$8 C^2 t \zeta \big ({\lvert {x} \rvert }\big ) \leq 1$
. Then, by (2.10) and (4.5),
 $$ \begin{align*} \frac{1}{t} \geq 8 C^2 \zeta\big({\lvert {x} \rvert} \big) \geq 4C^2 \varphi^*\bigg(\frac{1}{{\lvert {x} \rvert}}\bigg) \geq \varphi^*\bigg(\frac{2 C}{{\lvert {x} \rvert}} \bigg); \end{align*} $$
$$ \begin{align*} \frac{1}{t} \geq 8 C^2 \zeta\big({\lvert {x} \rvert} \big) \geq 4C^2 \varphi^*\bigg(\frac{1}{{\lvert {x} \rvert}}\bigg) \geq \varphi^*\bigg(\frac{2 C}{{\lvert {x} \rvert}} \bigg); \end{align*} $$
that is,
 $$ \begin{align} {\lvert {x} \rvert} \geq \frac{2 C}{\varphi^{-1}(1/t)}. \end{align} $$
$$ \begin{align} {\lvert {x} \rvert} \geq \frac{2 C}{\varphi^{-1}(1/t)}. \end{align} $$
Hence, by (4.38),
 $$ \begin{align*} \Big|x + t\Big( b_{1/\psi^{-1}(1/t)} - b_{1/\varphi^{-1}(1/t)}\Big)\Big| \geq {\lvert {x} \rvert} - \frac{C}{\varphi^{-1}(1/t)} \geq \frac{{\lvert {x} \rvert}}{2}, \end{align*} $$
$$ \begin{align*} \Big|x + t\Big( b_{1/\psi^{-1}(1/t)} - b_{1/\varphi^{-1}(1/t)}\Big)\Big| \geq {\lvert {x} \rvert} - \frac{C}{\varphi^{-1}(1/t)} \geq \frac{{\lvert {x} \rvert}}{2}, \end{align*} $$
which, together with monotonicity and the doubling property of
![]() $\zeta $
, gives
$\zeta $
, gives
 $$ \begin{align*} \zeta\Big(\big| x + t \big(b_{1/\psi^{-1}(1/t)} - b_{1/\varphi^{-1}(1/t)}\big)\big| \Big) \lesssim \zeta\big( {\lvert {x} \rvert} \big). \end{align*} $$
$$ \begin{align*} \zeta\Big(\big| x + t \big(b_{1/\psi^{-1}(1/t)} - b_{1/\varphi^{-1}(1/t)}\big)\big| \Big) \lesssim \zeta\big( {\lvert {x} \rvert} \big). \end{align*} $$
Similarly, if
 $t \eta ({\lvert {x} \rvert }) \leq \tfrac {A \epsilon }{2} \varphi ^{-1}(1/t)$
, then
$t \eta ({\lvert {x} \rvert }) \leq \tfrac {A \epsilon }{2} \varphi ^{-1}(1/t)$
, then
 $$ \begin{align*} {\lvert {x} \rvert} \varphi^{-1}(1/t) \geq \epsilon^{-1/3}; \end{align*} $$
$$ \begin{align*} {\lvert {x} \rvert} \varphi^{-1}(1/t) \geq \epsilon^{-1/3}; \end{align*} $$
thus, by taking
![]() $\epsilon = (2C)^{-3}$
, we obtain (4.39). Hence, by monotonicity and the doubling property of
$\epsilon = (2C)^{-3}$
, we obtain (4.39). Hence, by monotonicity and the doubling property of
![]() $\eta $
, we again obtain
$\eta $
, we again obtain
 $$ \begin{align*} \eta\bigg(\Big| x + t\Big( b_{1/\psi^{-1}(1/t)} - b_{1/\varphi^{-1}(1/t)}\Big) \Big|\bigg) \lesssim \eta({\lvert {x} \rvert}). \end{align*} $$
$$ \begin{align*} \eta\bigg(\Big| x + t\Big( b_{1/\psi^{-1}(1/t)} - b_{1/\varphi^{-1}(1/t)}\Big) \Big|\bigg) \lesssim \eta({\lvert {x} \rvert}). \end{align*} $$
4.2. Estimates from below
In this section we develop estimates from below on the density
![]() $p(t, \: \cdot \:)$
. The main result is Theorem 4.11. Its proof is inspired by the ideas from [Reference Picard42], see also [Reference Grzywny and Szczypkowski23]. Thanks to Theorem 3.3, we can generalise results obtained in [Reference Picard42] to the case when
$p(t, \: \cdot \:)$
. The main result is Theorem 4.11. Its proof is inspired by the ideas from [Reference Picard42], see also [Reference Grzywny and Szczypkowski23]. Thanks to Theorem 3.3, we can generalise results obtained in [Reference Picard42] to the case when
![]() $-\phi ^{\prime \prime }$
satisfies the weak lower scaling of index
$-\phi ^{\prime \prime }$
satisfies the weak lower scaling of index
![]() $\alpha -2$
for
$\alpha -2$
for
![]() $\alpha>0$
together with a certain additional condition. We use the following variant of the celebrated Pruitt’s result [Reference Pruitt45, Section 3] adapted to subordinators.
$\alpha>0$
together with a certain additional condition. We use the following variant of the celebrated Pruitt’s result [Reference Pruitt45, Section 3] adapted to subordinators.
Proposition 4.10. Let
![]() $\mathbf {T}$
be a subordinator with the Lévy–Khintchine exponent
$\mathbf {T}$
be a subordinator with the Lévy–Khintchine exponent
 $$ \begin{align*} \psi(\xi) = -i\xi b - \int_{(0, \infty)} \big(e^{i\xi x} - 1\big) \: \nu({\textrm{d}} x). \end{align*} $$
$$ \begin{align*} \psi(\xi) = -i\xi b - \int_{(0, \infty)} \big(e^{i\xi x} - 1\big) \: \nu({\textrm{d}} x). \end{align*} $$
Then there is an absolute constant
![]() $c>0$
such that for all
$c>0$
such that for all
![]() $\lambda> 0$
and
$\lambda> 0$
and
![]() $t> 0$
,
$t> 0$
,
 $$ \begin{align*} \mathbb{P} \Big( \mathop{\mathrm{sup}}\limits_{0 \leq s \leq t} \big|T_s- s b_\lambda \big|\geq \lambda \Big) \leq ct h(\lambda). \end{align*} $$
$$ \begin{align*} \mathbb{P} \Big( \mathop{\mathrm{sup}}\limits_{0 \leq s \leq t} \big|T_s- s b_\lambda \big|\geq \lambda \Big) \leq ct h(\lambda). \end{align*} $$
Proof. We are going to apply the estimates [Reference Pruitt45, (3.2)]. To do so, we need to express the Lévy–Khintchine exponent of
![]() $T_s - s b_\lambda $
in the form used in [Reference Pruitt45, Section 3], namely,
$T_s - s b_\lambda $
in the form used in [Reference Pruitt45, Section 3], namely,
 $$ \begin{align*} \tilde{\psi}(\xi) &= \psi(\xi) + i \xi b_\lambda \\ &= -i\xi \bigg(b - b_\lambda + \int_{(0, \infty)} \frac{y}{1 + |y|^2} \: \nu({\textrm{d}} y) \bigg) - \int_{(0, \infty)} \bigg(e^{i\xi y} - 1 - \frac{i y \xi}{1 + |y|^2} \bigg) \: \nu({\textrm{d}} y). \end{align*} $$
$$ \begin{align*} \tilde{\psi}(\xi) &= \psi(\xi) + i \xi b_\lambda \\ &= -i\xi \bigg(b - b_\lambda + \int_{(0, \infty)} \frac{y}{1 + |y|^2} \: \nu({\textrm{d}} y) \bigg) - \int_{(0, \infty)} \bigg(e^{i\xi y} - 1 - \frac{i y \xi}{1 + |y|^2} \bigg) \: \nu({\textrm{d}} y). \end{align*} $$
Since
 $$ \begin{align*} \int_{(0, \lambda]} \frac{y |y|^2}{1+|y|^2} \: \nu({\textrm{d}} y) - \int_{(\lambda, \infty)} \frac{y}{1+|y|^2} \: \nu({\textrm{d}} y) = \int_{(0, \lambda]} y \: \nu({\textrm{d}} y) - \int_{(0, \infty)} \frac{y}{1+|y|^2} \: \nu({\textrm{d}} y), \end{align*} $$
$$ \begin{align*} \int_{(0, \lambda]} \frac{y |y|^2}{1+|y|^2} \: \nu({\textrm{d}} y) - \int_{(\lambda, \infty)} \frac{y}{1+|y|^2} \: \nu({\textrm{d}} y) = \int_{(0, \lambda]} y \: \nu({\textrm{d}} y) - \int_{(0, \infty)} \frac{y}{1+|y|^2} \: \nu({\textrm{d}} y), \end{align*} $$
we have
 $$ \begin{align*} M(\lambda) &= \frac{1}{\lambda} \bigg| b - b_\lambda + \int_{(0, \infty)} \frac{y}{1 + |y|^2} \: \nu({\textrm{d}} y) + \int_{(0, \lambda]} \frac{y |y|^2}{1+|y|^2} \: \nu({\textrm{d}} y) - \int_{(\lambda, \infty)} \frac{y}{1+|y|^2} \: \nu({\textrm{d}} y) \bigg| \\ &= \frac{1}{\lambda} \bigg| b - b_\lambda + \int_{(0, \lambda]} y \: \nu({\textrm{d}} y) \bigg| = 0. \end{align*} $$
$$ \begin{align*} M(\lambda) &= \frac{1}{\lambda} \bigg| b - b_\lambda + \int_{(0, \infty)} \frac{y}{1 + |y|^2} \: \nu({\textrm{d}} y) + \int_{(0, \lambda]} \frac{y |y|^2}{1+|y|^2} \: \nu({\textrm{d}} y) - \int_{(\lambda, \infty)} \frac{y}{1+|y|^2} \: \nu({\textrm{d}} y) \bigg| \\ &= \frac{1}{\lambda} \bigg| b - b_\lambda + \int_{(0, \lambda]} y \: \nu({\textrm{d}} y) \bigg| = 0. \end{align*} $$
Hence, by [Reference Pruitt45, (3.2)],
 $$ \begin{align*} \mathbb{P} \Big( \mathop{\mathrm{sup}}\limits_{0 \leq s \leq t} \big|T_s- s b_\lambda \big|\geq \lambda \Big) \leq c s h(\lambda), \end{align*} $$
$$ \begin{align*} \mathbb{P} \Big( \mathop{\mathrm{sup}}\limits_{0 \leq s \leq t} \big|T_s- s b_\lambda \big|\geq \lambda \Big) \leq c s h(\lambda), \end{align*} $$
as desired.
Theorem 4.11. Let
![]() $\mathbf {T}$
be a subordinator with the Laplace exponent
$\mathbf {T}$
be a subordinator with the Laplace exponent
![]() $\phi $
. Suppose that
$\phi $
. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
, and assume that one of the following conditions holds true:
$\alpha>0$
, and assume that one of the following conditions holds true:
-
(i)
 $-\phi ^{\prime \prime } \in \mathrm {WUSC}(\beta -2,C,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WUSC}(\beta -2,C,x_0)$
for some
 $C\geq 1$
and
$C\geq 1$
and
 $\alpha \leq \beta <1$
, or
$\alpha \leq \beta <1$
, or -
(ii)
 $-\phi ^{\prime \prime }$
is a function regularly varying at infinity with index
$-\phi ^{\prime \prime }$
is a function regularly varying at infinity with index
 $-1$
. If
$-1$
. If
 $x_0 = 0$
we also assume that
$x_0 = 0$
we also assume that
 $-\phi ^{\prime \prime }$
is regularly varying at zero with index
$-\phi ^{\prime \prime }$
is regularly varying at zero with index
 $-1$
.
$-1$
.
Then there is
![]() $M_0>1$
such that for each
$M_0>1$
such that for each
![]() $M \geq M_0$
there exists
$M \geq M_0$
there exists
![]() $\rho _0> 0$
, so that for all
$\rho _0> 0$
, so that for all
![]() $0 < \rho _1 < \rho _0$
,
$0 < \rho _1 < \rho _0$
,
![]() $0 < \rho _2$
there is
$0 < \rho _2$
there is
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $t \in (0, 1/\varphi (x_0))$
and all
$t \in (0, 1/\varphi (x_0))$
and all
![]() $x> 0$
satisfying
$x> 0$
satisfying
 $$ \begin{align*} -\frac{\rho_1}{\varphi^{-1}(1/t)} \leq x - t \phi'\big(\varphi^{-1}({M}/t)\big) \leq \frac{\rho_2}{\varphi^{-1}(1/t)}, \end{align*} $$
$$ \begin{align*} -\frac{\rho_1}{\varphi^{-1}(1/t)} \leq x - t \phi'\big(\varphi^{-1}({M}/t)\big) \leq \frac{\rho_2}{\varphi^{-1}(1/t)}, \end{align*} $$
we have
Remark 4.12. From the proof of Theorem 4.11 it stems that if
![]() $x_0=0$
, one can obtain the same statement under the condition that
$x_0=0$
, one can obtain the same statement under the condition that
![]() $-\phi ^{\prime \prime }$
is
$-\phi ^{\prime \prime }$
is
![]() $(-1)$
-regular at infinity and satisfies upper scaling at
$(-1)$
-regular at infinity and satisfies upper scaling at
![]() $0$
with
$0$
with
![]() $\alpha \leq \beta < 1$
. Alternatively, one can assume that
$\alpha \leq \beta < 1$
. Alternatively, one can assume that
![]() $-\phi ^{\prime \prime }$
satisfies upper scaling at infinity with
$-\phi ^{\prime \prime }$
satisfies upper scaling at infinity with
![]() $\alpha \leq \beta < 1$
and varies regularly at zero with index
$\alpha \leq \beta < 1$
and varies regularly at zero with index
![]() $-1$
. The same remark applies to Proposition 4.14.
$-1$
. The same remark applies to Proposition 4.14.
Proof. First let us observe that it is enough to prove that (4.40) holds true for all
![]() $t \in (0,1/\varphi (x_0))$
and all
$t \in (0,1/\varphi (x_0))$
and all
![]() $x> 0$
satisfying
$x> 0$
satisfying
 $$ \begin{align*} -\frac{\rho_1}{\varphi^{-1}(M/t)} \leq x - t \phi'\big(\varphi^{-1}({M}/t)\big) \leq \frac{\rho_2}{\varphi^{-1}(M/t)}. \end{align*} $$
$$ \begin{align*} -\frac{\rho_1}{\varphi^{-1}(M/t)} \leq x - t \phi'\big(\varphi^{-1}({M}/t)\big) \leq \frac{\rho_2}{\varphi^{-1}(M/t)}. \end{align*} $$
Indeed, since
![]() $\varphi ^{-1}$
is nondecreasing and has upper scaling property (see Proposition 4.3), it has a doubling property. Hence, the lemma will follow immediately with possibly modified
$\varphi ^{-1}$
is nondecreasing and has upper scaling property (see Proposition 4.3), it has a doubling property. Hence, the lemma will follow immediately with possibly modified
![]() $\rho _0$
.
$\rho _0$
.
Without loss of generality, we can assume that
![]() $b = 0$
. Let
$b = 0$
. Let
![]() $\lambda> 0$
, whose value will be specified later. We decompose the Lévy measure
$\lambda> 0$
, whose value will be specified later. We decompose the Lévy measure
![]() $\nu ({\mathrm {d}} x)$
as follows: Let
$\nu ({\mathrm {d}} x)$
as follows: Let
![]() $\nu _1({\mathrm {d}} x)$
be the restriction of
$\nu _1({\mathrm {d}} x)$
be the restriction of
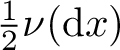 $\tfrac 12 \nu ({\mathrm {d}} x)$
to the interval
$\tfrac 12 \nu ({\mathrm {d}} x)$
to the interval
![]() $(0,\lambda ]$
and
$(0,\lambda ]$
and
We set
 $$ \begin{align*} \phi_1(u) = \int_{(0, \infty)} \big(1 - e^{-u s}\big) \: \nu_1({\textrm{d}} s), \qquad \phi_2(u) = \int_{(0, \infty)} \big(1 - e^{-u s}\big) \: \nu_2({\textrm{d}} s). \end{align*} $$
$$ \begin{align*} \phi_1(u) = \int_{(0, \infty)} \big(1 - e^{-u s}\big) \: \nu_1({\textrm{d}} s), \qquad \phi_2(u) = \int_{(0, \infty)} \big(1 - e^{-u s}\big) \: \nu_2({\textrm{d}} s). \end{align*} $$
Let us denote by
![]() $\mathbf {T}^{(j)}$
the subordinator having the Laplace exponent
$\mathbf {T}^{(j)}$
the subordinator having the Laplace exponent
![]() $\phi _j$
, for
$\phi _j$
, for
![]() $j \in \{ 1, 2 \}$
. Let
$j \in \{ 1, 2 \}$
. Let
![]() $\psi _j(\xi ) = \phi _j(-i\xi )$
. Notice that
$\psi _j(\xi ) = \phi _j(-i\xi )$
. Notice that
 $\tfrac 12 \nu \leq \nu _2 \leq \nu $
; thus,
$\tfrac 12 \nu \leq \nu _2 \leq \nu $
; thus,
 $$ \begin{align*} \tfrac12 \phi \leq \phi_2 \leq \phi, \end{align*} $$
$$ \begin{align*} \tfrac12 \phi \leq \phi_2 \leq \phi, \end{align*} $$
and for every
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
 $$ \begin{align} \tfrac12 (-1)^{n+1} \phi^{(n)} \leq (-1)^{n+1} \phi_2^{(n)} \leq (-1)^{n+1} \phi^{(n)}. \end{align} $$
$$ \begin{align} \tfrac12 (-1)^{n+1} \phi^{(n)} \leq (-1)^{n+1} \phi_2^{(n)} \leq (-1)^{n+1} \phi^{(n)}. \end{align} $$
Therefore, for all
![]() $u> 0$
,
$u> 0$
,
 $$ \begin{align} \tfrac12 \varphi(u) \leq \varphi_2(u) \leq \varphi(u). \end{align} $$
$$ \begin{align} \tfrac12 \varphi(u) \leq \varphi_2(u) \leq \varphi(u). \end{align} $$
Next, by Theorem 3.3, the random variables
 $T_t^{(2)}$
and
$T_t^{(2)}$
and
![]() $T_t$
are absolutely continuous. Let us denote by
$T_t$
are absolutely continuous. Let us denote by
![]() $p^{(2)}(t, \:\cdot \:)$
and
$p^{(2)}(t, \:\cdot \:)$
and
![]() $p(t, \:\cdot \:)$
the densities of
$p(t, \:\cdot \:)$
the densities of
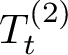 $T^{(2)}_t$
and
$T^{(2)}_t$
and
![]() $T_t$
, respectively.
$T_t$
, respectively.
Let
![]() $M \geq 2 M_0+1$
, where
$M \geq 2 M_0+1$
, where
![]() $M_0$
is determined in Corollary 3.5 for the process
$M_0$
is determined in Corollary 3.5 for the process
![]() $\mathbf {T}^{(2)}$
. For
$\mathbf {T}^{(2)}$
. For
![]() $0 < t < 1/\varphi (x_0)$
, we set
$0 < t < 1/\varphi (x_0)$
, we set
 $$ \begin{align*} x_t = t \phi_2'\big(\varphi^{-1}(M/t)\big). \end{align*} $$
$$ \begin{align*} x_t = t \phi_2'\big(\varphi^{-1}(M/t)\big). \end{align*} $$
Since
![]() $\varphi ^{-1}(M/t)> x_0$
, we have
$\varphi ^{-1}(M/t)> x_0$
, we have
 $$ \begin{align*} \frac{x_t}{t} = \phi_2'\big(\varphi^{-1}(M/t)\big) \leq \phi'_2(x_0). \end{align*} $$
$$ \begin{align*} \frac{x_t}{t} = \phi_2'\big(\varphi^{-1}(M/t)\big) \leq \phi'_2(x_0). \end{align*} $$
Let
Then, by (4.42) we get
 $$ \begin{align*} \varphi_2(w_2) \geq \frac12 \varphi \big( \varphi^{-1}(M/t) \big) = \frac{M}{2t} \geq \frac{M_0}{t}. \end{align*} $$
$$ \begin{align*} \varphi_2(w_2) \geq \frac12 \varphi \big( \varphi^{-1}(M/t) \big) = \frac{M}{2t} \geq \frac{M_0}{t}. \end{align*} $$
Moreover, by Corollary 4.5 together with (4.42) we get
 $$ \begin{align*} t\big( \phi_2(w_2) - w_2 \phi_2'(w_2) \big) \lesssim t \varphi_2\big(w_2\big) \lesssim 1. \end{align*} $$
$$ \begin{align*} t\big( \phi_2(w_2) - w_2 \phi_2'(w_2) \big) \lesssim t \varphi_2\big(w_2\big) \lesssim 1. \end{align*} $$
Hence, by Corollary 3.5,
 $$ \begin{align} p^{(2)}(t, x_t) \gtrsim \frac{1}{\sqrt{t (-\phi_2^{\prime\prime})(w_2)}}. \end{align} $$
$$ \begin{align} p^{(2)}(t, x_t) \gtrsim \frac{1}{\sqrt{t (-\phi_2^{\prime\prime})(w_2)}}. \end{align} $$
Notice that, by (4.41) and Remark 3.4, the implied constant in (4.43) is independent of t and
![]() $\lambda $
. Since
$\lambda $
. Since
 $$ \begin{align*} (-\phi_2^{\prime\prime})(w_2) \leq (-\phi^{\prime\prime})\big( \varphi^{-1}(M/t)\big) =\frac{M}{t \big(\varphi^{-1}(M/t)\big)^{2}}, \end{align*} $$
$$ \begin{align*} (-\phi_2^{\prime\prime})(w_2) \leq (-\phi^{\prime\prime})\big( \varphi^{-1}(M/t)\big) =\frac{M}{t \big(\varphi^{-1}(M/t)\big)^{2}}, \end{align*} $$
by (4.43) and monotonicity of
![]() $\varphi ^{-1}$
, we get
$\varphi ^{-1}$
, we get
 $$ \begin{align} p^{(2)}(t, x_t) \geq C_1 \varphi^{-1} (1/t), \end{align} $$
$$ \begin{align} p^{(2)}(t, x_t) \geq C_1 \varphi^{-1} (1/t), \end{align} $$
for some constant
![]() $C_1> 0$
.
$C_1> 0$
.
Next, by the Fourier inversion formula
 $$ \begin{align*} \mathop{\mathrm{sup}}\limits_{x \in \mathbb{R}} \big| \partial_x p^{(2)}(t,x) \big| &\lesssim \int_{\mathbb{R}} e^{-t \Re \psi_2(\xi)} {\lvert {\xi} \rvert} {\: \rm d} \xi \\ &\lesssim \int_{\mathbb{R}} e^{-\frac{t}{2} \Re \psi(\xi)} {\lvert {\xi} \rvert} {\: \rm d} \xi; \end{align*} $$
$$ \begin{align*} \mathop{\mathrm{sup}}\limits_{x \in \mathbb{R}} \big| \partial_x p^{(2)}(t,x) \big| &\lesssim \int_{\mathbb{R}} e^{-t \Re \psi_2(\xi)} {\lvert {\xi} \rvert} {\: \rm d} \xi \\ &\lesssim \int_{\mathbb{R}} e^{-\frac{t}{2} \Re \psi(\xi)} {\lvert {\xi} \rvert} {\: \rm d} \xi; \end{align*} $$
thus, by [Reference Grzywny and Szczypkowski23, Proposition 3.4] and Propositions 4.2 and 4.3 we see that there is
![]() $C_2> 0$
such that for all
$C_2> 0$
such that for all
![]() $t \in (0, 1/\varphi (x_0))$
,
$t \in (0, 1/\varphi (x_0))$
,
 $$ \begin{align*} \mathop{\mathrm{sup}}\limits_{x \in \mathbb{R}} \big| \partial_x p^{(2)}(t,x) \big| \leq C_2 \big(\varphi^{-1}(1/t)\big)^2. \end{align*} $$
$$ \begin{align*} \mathop{\mathrm{sup}}\limits_{x \in \mathbb{R}} \big| \partial_x p^{(2)}(t,x) \big| \leq C_2 \big(\varphi^{-1}(1/t)\big)^2. \end{align*} $$
By the mean value theorem, for
![]() $y \in \mathbb {R}$
, we get
$y \in \mathbb {R}$
, we get
 $$ \begin{align*} \big| p^{(2)}(t, y + x_t) - p^{(2)}(t, x_t) \big| \leq C_2 {\lvert {y} \rvert} \big(\varphi^{-1}(1/t)\big)^2. \end{align*} $$
$$ \begin{align*} \big| p^{(2)}(t, y + x_t) - p^{(2)}(t, x_t) \big| \leq C_2 {\lvert {y} \rvert} \big(\varphi^{-1}(1/t)\big)^2. \end{align*} $$
Hence, for
![]() $y \in \mathbb {R}$
satisfying
$y \in \mathbb {R}$
satisfying
 $$ \begin{align*} {\lvert {y} \rvert} \leq \frac{C_1} {2 C_2 \varphi^{-1}(1/t)}, \end{align*} $$
$$ \begin{align*} {\lvert {y} \rvert} \leq \frac{C_1} {2 C_2 \varphi^{-1}(1/t)}, \end{align*} $$
by (4.44), we get
 $$ \begin{align*} p^{(2)}(t, y + x_t) &\geq p^{(2)}(t, x_t) - C_2 {\lvert {y} \rvert} \big(\varphi^{-1}(1/t)\big)^2 \\ &\geq \frac{C_1}{2} \varphi^{-1}(1/t). \end{align*} $$
$$ \begin{align*} p^{(2)}(t, y + x_t) &\geq p^{(2)}(t, x_t) - C_2 {\lvert {y} \rvert} \big(\varphi^{-1}(1/t)\big)^2 \\ &\geq \frac{C_1}{2} \varphi^{-1}(1/t). \end{align*} $$
Therefore,
 $$ \begin{align*} p(t,x) &= \int_{\mathbb{R}} p^{(2)}(t,x-y) \mathbb{P} \big( T_t^{(1)}\in {\: \rm d} y \big) \\ &\geq \frac{C_1}{2} \varphi^{-1}(1/t) \cdot \mathbb{P} \bigg( \big|x - x_t - T_t^{(1)} \big| \leq \frac{C_0}{\varphi^{-1}(1/t)} \bigg) \\ &\geq \frac{C_1}{2} \varphi^{-1}(1/t) \cdot \mathbb{P} \bigg( \big|x - x_t - T_t^{(1)} \big| \leq \frac{C_0}{\varphi^{-1}(M/t)} \bigg) \\ &= \frac{C_1}{2} \varphi^{-1}(1/t) \cdot \mathbb{P} \bigg( \Big|x - \tilde{x}_t - \big( \tfrac12 tb_{\lambda} - (\tilde{x}_t - x_t) \big) - \big(T_t^{(1)}-\tfrac12 tb_{\lambda}\big) \Big| \leq \frac{C_0}{\varphi^{-1}(M/t)} \bigg), \end{align*} $$
$$ \begin{align*} p(t,x) &= \int_{\mathbb{R}} p^{(2)}(t,x-y) \mathbb{P} \big( T_t^{(1)}\in {\: \rm d} y \big) \\ &\geq \frac{C_1}{2} \varphi^{-1}(1/t) \cdot \mathbb{P} \bigg( \big|x - x_t - T_t^{(1)} \big| \leq \frac{C_0}{\varphi^{-1}(1/t)} \bigg) \\ &\geq \frac{C_1}{2} \varphi^{-1}(1/t) \cdot \mathbb{P} \bigg( \big|x - x_t - T_t^{(1)} \big| \leq \frac{C_0}{\varphi^{-1}(M/t)} \bigg) \\ &= \frac{C_1}{2} \varphi^{-1}(1/t) \cdot \mathbb{P} \bigg( \Big|x - \tilde{x}_t - \big( \tfrac12 tb_{\lambda} - (\tilde{x}_t - x_t) \big) - \big(T_t^{(1)}-\tfrac12 tb_{\lambda}\big) \Big| \leq \frac{C_0}{\varphi^{-1}(M/t)} \bigg), \end{align*} $$
where we have set
![]() $C_0=C_1(2C_2)^{-1}$
and
$C_0=C_1(2C_2)^{-1}$
and
 $$ \begin{align*} \tilde{x}_t = t\phi' \big(\varphi^{-1}(M/t)\big). \end{align*} $$
$$ \begin{align*} \tilde{x}_t = t\phi' \big(\varphi^{-1}(M/t)\big). \end{align*} $$
Let
 $\rho _0 = \tfrac {1}{2} C_0$
and
$\rho _0 = \tfrac {1}{2} C_0$
and
 $$ \begin{align} \lambda = \frac{1}{\varphi^{-1}(M/t)}. \end{align} $$
$$ \begin{align} \lambda = \frac{1}{\varphi^{-1}(M/t)}. \end{align} $$
We have
 $$ \begin{align*} \frac{1}{2} tb_{\lambda} - (\tilde{x}_t - x_t) &= \frac12tb_{\lambda} - t\phi_1'(1/\lambda) \\ &= \frac{t}{2} \int_{(0,\lambda]} s\big(1-e^{-s/\lambda} \big) \: \nu({\textrm{d}} s). \end{align*} $$
$$ \begin{align*} \frac{1}{2} tb_{\lambda} - (\tilde{x}_t - x_t) &= \frac12tb_{\lambda} - t\phi_1'(1/\lambda) \\ &= \frac{t}{2} \int_{(0,\lambda]} s\big(1-e^{-s/\lambda} \big) \: \nu({\textrm{d}} s). \end{align*} $$
Thus,
 $\tfrac 12 tb_{\lambda } - (\tilde {x}_t - x_t)$
is nonnegative, and in view of (4.2) and (4.45),
$\tfrac 12 tb_{\lambda } - (\tilde {x}_t - x_t)$
is nonnegative, and in view of (4.2) and (4.45),
 $$ \begin{align} \nonumber \tfrac12 tb_{\lambda} - (\tilde{x}_t - x_t) &\leq C_3 t \lambda \varphi(1/\lambda) \\ &= \frac{C_3M}{\varphi^{-1}(M/t)}, \end{align} $$
$$ \begin{align} \nonumber \tfrac12 tb_{\lambda} - (\tilde{x}_t - x_t) &\leq C_3 t \lambda \varphi(1/\lambda) \\ &= \frac{C_3M}{\varphi^{-1}(M/t)}, \end{align} $$
for some constant
![]() $C_3>0$
. Next, setting
$C_3>0$
. Next, setting
 $$ \begin{align*} \rho(t) = \lambda^{-1}\Big( \tfrac12 tb_{\lambda} - (\tilde{x}_t - x_t)\Big), \end{align*} $$
$$ \begin{align*} \rho(t) = \lambda^{-1}\Big( \tfrac12 tb_{\lambda} - (\tilde{x}_t - x_t)\Big), \end{align*} $$
we get
 $$ \begin{align} \nonumber & \inf_{t \in (0, 1/\varphi(x_0))}{\bigg\{ \mathbb{P} \bigg( \Big| x -\tilde{x}_t - \lambda\rho(t) - \big( T_t^{(1)} - \tfrac12 tb_{\lambda}\big) \Big| \leq C_0 \lambda \bigg) \colon x \geq 0, -\rho_1 \lambda \leq x- \tilde{x}_t \leq \rho_2\lambda \bigg\}} \\ &\qquad\qquad\geq \inf_{t \in (0, 1/\varphi(x_0))}{ \Big\{ \mathbb{P}\left( \Big| y - \lambda^{-1} \big( T_t^{(1)} -\tfrac12 tb_{\lambda} \big) \Big| \leq C_0 \right) \colon -\rho_1 -\rho(t) \leq y \leq \rho_2 \Big\}}. \end{align} $$
$$ \begin{align} \nonumber & \inf_{t \in (0, 1/\varphi(x_0))}{\bigg\{ \mathbb{P} \bigg( \Big| x -\tilde{x}_t - \lambda\rho(t) - \big( T_t^{(1)} - \tfrac12 tb_{\lambda}\big) \Big| \leq C_0 \lambda \bigg) \colon x \geq 0, -\rho_1 \lambda \leq x- \tilde{x}_t \leq \rho_2\lambda \bigg\}} \\ &\qquad\qquad\geq \inf_{t \in (0, 1/\varphi(x_0))}{ \Big\{ \mathbb{P}\left( \Big| y - \lambda^{-1} \big( T_t^{(1)} -\tfrac12 tb_{\lambda} \big) \Big| \leq C_0 \right) \colon -\rho_1 -\rho(t) \leq y \leq \rho_2 \Big\}}. \end{align} $$
Hence, the problem is reduced to showing that the infimum above is positive. Let us consider a collection
![]() $\{Y_t \colon t \in (0, 1/\varphi (x_0)) \}$
of infinitely divisible nonnegative random variables
$\{Y_t \colon t \in (0, 1/\varphi (x_0)) \}$
of infinitely divisible nonnegative random variables
 $Y_t = \lambda ^{-1}\big ( T^{(1)}_t-\tfrac 12 tb_{\lambda }\big )$
. The Lévy measure corresponding to
$Y_t = \lambda ^{-1}\big ( T^{(1)}_t-\tfrac 12 tb_{\lambda }\big )$
. The Lévy measure corresponding to
![]() $Y_t$
is
$Y_t$
is
 $$ \begin{align} \mu_t(B) = t \nu_1\big(\lambda B\big) \end{align} $$
$$ \begin{align} \mu_t(B) = t \nu_1\big(\lambda B\big) \end{align} $$
for any Borel subset
![]() $B \subset \mathbb {R}$
. Since for each
$B \subset \mathbb {R}$
. Since for each
![]() $R> 1$
,
$R> 1$
,
 $$ \begin{align*} b_{R \lambda}^{(1)} &= \int_{(0, R \lambda]} y \: \nu_1({\textrm{d}} y) \\ &= \frac{1}{2} \int_{(0, \lambda]} y \: \nu({\textrm{d}} y) = \frac{1}{2} b_\lambda, \end{align*} $$
$$ \begin{align*} b_{R \lambda}^{(1)} &= \int_{(0, R \lambda]} y \: \nu_1({\textrm{d}} y) \\ &= \frac{1}{2} \int_{(0, \lambda]} y \: \nu({\textrm{d}} y) = \frac{1}{2} b_\lambda, \end{align*} $$
by Proposition 4.10,
 $$ \begin{align*} \mathbb{P}\big(|Y_t| \geq R\big) &= \mathbb{P}\left(\Big| T_t^{(1)}-\tfrac12 tb_{\lambda} \Big| \geq R \lambda \right) \\ &\lesssim t \int_{(0, \infty)} \min{\big\{1, R^{-2} \lambda^{-2} s^2\big\}} \: \nu_1({\textrm{d}} s); \end{align*} $$
$$ \begin{align*} \mathbb{P}\big(|Y_t| \geq R\big) &= \mathbb{P}\left(\Big| T_t^{(1)}-\tfrac12 tb_{\lambda} \Big| \geq R \lambda \right) \\ &\lesssim t \int_{(0, \infty)} \min{\big\{1, R^{-2} \lambda^{-2} s^2\big\}} \: \nu_1({\textrm{d}} s); \end{align*} $$
thus,
 $$ \begin{align*} \mathbb{P}\big(|Y_t| \geq R\big) &\lesssim t \lambda^{-2} R^{-2} \int_{(0, \lambda]} s^2 \: \nu({\textrm{d}} s) \\ &\lesssim t R^{-2} h(\lambda) \\ &\lesssim t R^{-2} \varphi(1/\lambda), \end{align*} $$
$$ \begin{align*} \mathbb{P}\big(|Y_t| \geq R\big) &\lesssim t \lambda^{-2} R^{-2} \int_{(0, \lambda]} s^2 \: \nu({\textrm{d}} s) \\ &\lesssim t R^{-2} h(\lambda) \\ &\lesssim t R^{-2} \varphi(1/\lambda), \end{align*} $$
where in the last estimate we have used (4.2). Therefore, recalling (4.45), we conclude that the collection is tight. Next, let
 $\big ((Y_{t_n}, y_n) \colon n \in \mathbb {N}\big )$
be a sequence realising the infimum in (4.47). By the Prokhorov theorem, we can assume that
$\big ((Y_{t_n}, y_n) \colon n \in \mathbb {N}\big )$
be a sequence realising the infimum in (4.47). By the Prokhorov theorem, we can assume that
![]() $(Y_{t_n} \colon n \in \mathbb {N})$
is weakly convergent to the random variable
$(Y_{t_n} \colon n \in \mathbb {N})$
is weakly convergent to the random variable
![]() $Y_0$
. We note that
$Y_0$
. We note that
![]() $Y_{t_n}$
has the probability distribution supported in
$Y_{t_n}$
has the probability distribution supported in
 $\big [-\tfrac 12t_n\lambda _n^{-1}b_{\lambda _n}, \infty \big )$
where
$\big [-\tfrac 12t_n\lambda _n^{-1}b_{\lambda _n}, \infty \big )$
where
![]() $\lambda _n$
is defined as
$\lambda _n$
is defined as
![]() $\lambda $
corresponding to
$\lambda $
corresponding to
![]() $t_n$
.
$t_n$
.
Suppose that
![]() $(t_n : n \in \mathbb {N})$
contains a subsequence convergent to
$(t_n : n \in \mathbb {N})$
contains a subsequence convergent to
![]() $t_0> 0$
. Then
$t_0> 0$
. Then
![]() $Y_0 = Y_{t_0}$
and the support of its probability distribution equals
$Y_0 = Y_{t_0}$
and the support of its probability distribution equals
 $\big [-\tfrac 12t_0\lambda _0^{-1}b_{\lambda _0}, \infty \big )$
. Since
$\big [-\tfrac 12t_0\lambda _0^{-1}b_{\lambda _0}, \infty \big )$
. Since
 $\rho (t_0) \leq \tfrac 12t_0\lambda _0^{-1}b_{\lambda _0}$
, we easily conclude that the infimum in (4.47) is positive.
$\rho (t_0) \leq \tfrac 12t_0\lambda _0^{-1}b_{\lambda _0}$
, we easily conclude that the infimum in (4.47) is positive.
Hence, it remains to investigate the case when
![]() $(t_n \colon n \in \mathbb {N})$
has no positive accumulation points. If zero is the only accumulation point, then
$(t_n \colon n \in \mathbb {N})$
has no positive accumulation points. If zero is the only accumulation point, then
![]() $(\lambda _n \colon n \in \mathbb {N})$
has a subsequence convergent to zero. Otherwise,
$(\lambda _n \colon n \in \mathbb {N})$
has a subsequence convergent to zero. Otherwise,
![]() $(t_n)$
diverges to infinity; thus,
$(t_n)$
diverges to infinity; thus,
![]() $x_0 = 0$
and
$x_0 = 0$
and
![]() $(\lambda _n)$
contains a subsequence diverging to infinity. In view of (4.46),
$(\lambda _n)$
contains a subsequence diverging to infinity. In view of (4.46),
![]() $\rho (t)$
is uniformly bounded in t. Thus, after taking a subsequence, we may and do assume that there exists a limit
$\rho (t)$
is uniformly bounded in t. Thus, after taking a subsequence, we may and do assume that there exists a limit
 $$ \begin{align*} \tilde{\rho} = \lim_{n \to \infty} \rho(t_n). \end{align*} $$
$$ \begin{align*} \tilde{\rho} = \lim_{n \to \infty} \rho(t_n). \end{align*} $$
By compactness we can also assume that
![]() $(y_n \colon n \in \mathbb {N})$
converges to
$(y_n \colon n \in \mathbb {N})$
converges to
![]() $y_0 \in [-\rho _1-\tilde{\rho},\, \rho _2]$
. Consequently, to prove that the infimum in (4.47) is positive, it is sufficient to show that
$y_0 \in [-\rho _1-\tilde{\rho},\, \rho _2]$
. Consequently, to prove that the infimum in (4.47) is positive, it is sufficient to show that
 $$ \begin{align} \mathbb{P}\big(|y_0 - Y_0| \leq \tfrac{1}{2} C_0 \big)> 0. \end{align} $$
$$ \begin{align} \mathbb{P}\big(|y_0 - Y_0| \leq \tfrac{1}{2} C_0 \big)> 0. \end{align} $$
Observe that (4.49) is trivially satisfied if the support of the probability distribution of
![]() $Y_0$
is the whole real line. Therefore, we can assume that
$Y_0$
is the whole real line. Therefore, we can assume that
![]() $Y_0$
is purely non-Gaussian. In view of [Reference Sato47, Theorem 8.7], it is also infinitely divisible.
$Y_0$
is purely non-Gaussian. In view of [Reference Sato47, Theorem 8.7], it is also infinitely divisible.
Given
![]() $w \colon \mathbb {R} \rightarrow \mathbb {R}$
a continuous function satisfying
$w \colon \mathbb {R} \rightarrow \mathbb {R}$
a continuous function satisfying
 $$ \begin{align} \big| w(x) - 1 \big| \leq C' {\lvert {x} \rvert}, \qquad\text{and}\qquad \big| w(x)\big| \leq C' {\lvert {x} \rvert}^{-1}, \end{align} $$
$$ \begin{align} \big| w(x) - 1 \big| \leq C' {\lvert {x} \rvert}, \qquad\text{and}\qquad \big| w(x)\big| \leq C' {\lvert {x} \rvert}^{-1}, \end{align} $$
we write the Lévy–Khintchine exponent of
![]() $Y_{t_n}$
in the form
$Y_{t_n}$
in the form
 $$ \begin{align*} \psi_n(\xi) = -i \xi \gamma_n - \int_{(0, \infty)} \big(e^{i\xi s} -1 -i\xi s w(s) \big) \: \mu_{t_n}({\textrm{d}} s), \end{align*} $$
$$ \begin{align*} \psi_n(\xi) = -i \xi \gamma_n - \int_{(0, \infty)} \big(e^{i\xi s} -1 -i\xi s w(s) \big) \: \mu_{t_n}({\textrm{d}} s), \end{align*} $$
where
 $$ \begin{align*} \gamma_n = \int_{(0, \infty)} s w(s) \: \mu_{t_n}({\textrm{d}} s) - \tfrac12 \lambda_n^{-1}t_n b_{\lambda_n}. \end{align*} $$
$$ \begin{align*} \gamma_n = \int_{(0, \infty)} s w(s) \: \mu_{t_n}({\textrm{d}} s) - \tfrac12 \lambda_n^{-1}t_n b_{\lambda_n}. \end{align*} $$
Since
![]() $(Y_{t_n} : n \in \mathbb {N})$
converges weakly to
$(Y_{t_n} : n \in \mathbb {N})$
converges weakly to
![]() $Y_0$
, there are
$Y_0$
, there are
![]() $\gamma _0 \in \mathbb {R}$
and
$\gamma _0 \in \mathbb {R}$
and
![]() $\sigma $
-finite measure
$\sigma $
-finite measure
![]() $\mu _0$
on
$\mu _0$
on
![]() $(0, \infty )$
satisfying
$(0, \infty )$
satisfying
 $$ \begin{align*} \int_{(0, \infty)} \min{\big\{1, s^2 \big\}} \: \mu_0({\textrm{d}} s) < \infty, \end{align*} $$
$$ \begin{align*} \int_{(0, \infty)} \min{\big\{1, s^2 \big\}} \: \mu_0({\textrm{d}} s) < \infty, \end{align*} $$
such that the Lévy–Khintchine exponent of
![]() $Y_0$
is
$Y_0$
is
 $$ \begin{align*} \psi_0(\xi) = -i\xi \gamma_0 - \int_{(0, \infty)} \big(e^{i\xi s} -1 -i\xi s w(s) \big) \: \mu_0({\textrm{d}} s), \end{align*} $$
$$ \begin{align*} \psi_0(\xi) = -i\xi \gamma_0 - \int_{(0, \infty)} \big(e^{i\xi s} -1 -i\xi s w(s) \big) \: \mu_0({\textrm{d}} s), \end{align*} $$
where
 $$ \begin{align} \gamma_0 = \lim_{n \to \infty} \gamma_n. \end{align} $$
$$ \begin{align} \gamma_0 = \lim_{n \to \infty} \gamma_n. \end{align} $$
Moreover, for any bounded continuous function
![]() $f\colon \mathbb {R} \rightarrow \mathbb {R}$
vanishing in a neighbourhood of zero, we have
$f\colon \mathbb {R} \rightarrow \mathbb {R}$
vanishing in a neighbourhood of zero, we have
 $$ \begin{align} \lim_{n \to \infty} \int_{(0, \infty)} f(s) \: \mu_{t_n}({\textrm{d}} s) = \int_{(0, \infty)} f(s) \: \mu_{0}({\textrm{d}} s). \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \int_{(0, \infty)} f(s) \: \mu_{t_n}({\textrm{d}} s) = \int_{(0, \infty)} f(s) \: \mu_{0}({\textrm{d}} s). \end{align} $$
Next, let us fix w satisfying (4.50) which equals
![]() $1$
on
$1$
on
![]() $[0,1]$
. In view of (4.48) and the definition of
$[0,1]$
. In view of (4.48) and the definition of
![]() $\nu _1$
, the support of
$\nu _1$
, the support of
![]() $\mu _{t_n}$
is contained in
$\mu _{t_n}$
is contained in
![]() $[0, 1]$
. Hence,
$[0, 1]$
. Hence,
![]() $\gamma _n=0$
for every
$\gamma _n=0$
for every
![]() $n \in \mathbb {N}$
and, consequently,
$n \in \mathbb {N}$
and, consequently,
![]() $\gamma _0=0$
. We also conclude that
$\gamma _0=0$
. We also conclude that
![]() $\operatorname {\mathrm {supp}} \mu _0 \subset [0,1]$
.
$\operatorname {\mathrm {supp}} \mu _0 \subset [0,1]$
.
At this stage we consider the cases (i) and (ii) separately. In (ii) we need to distinguish two possibilities: if
![]() $(t_n)$
tends toward zero, then
$(t_n)$
tends toward zero, then
![]() $(\lambda _n)$
also approaches zero, and we impose that
$(\lambda _n)$
also approaches zero, and we impose that
![]() $-\phi ^{\prime \prime }$
is a function regularly varying at infinity with index
$-\phi ^{\prime \prime }$
is a function regularly varying at infinity with index
![]() $-1$
; otherwise,
$-1$
; otherwise,
![]() $(t_n)$
tends toward infinity as well as
$(t_n)$
tends toward infinity as well as
![]() $(\lambda _n)$
, and thus
$(\lambda _n)$
, and thus
![]() $x_0 = 0$
, and we additionally assume that
$x_0 = 0$
, and we additionally assume that
![]() $-\phi ^{\prime \prime }$
is a function regularly varying at zero with index
$-\phi ^{\prime \prime }$
is a function regularly varying at zero with index
![]() $-1$
. For the sake of clarity of presentation, we restrict attention to the first possibility only. In the second one the reasoning is analogous. We show that the support of the probability distribution of
$-1$
. For the sake of clarity of presentation, we restrict attention to the first possibility only. In the second one the reasoning is analogous. We show that the support of the probability distribution of
![]() $Y_0$
is the whole real line. By [Reference Sato47, Theorem 24.10], the latter can be deduced from
$Y_0$
is the whole real line. By [Reference Sato47, Theorem 24.10], the latter can be deduced from
 $$ \begin{align} \int_{(0, \infty)} \min\{1, s\} \: \mu_0({\textrm{d}} s) = \infty. \end{align} $$
$$ \begin{align} \int_{(0, \infty)} \min\{1, s\} \: \mu_0({\textrm{d}} s) = \infty. \end{align} $$
Since
![]() $\operatorname {\mathrm {supp}} \mu _0 \subset [0, 1]$
, for each
$\operatorname {\mathrm {supp}} \mu _0 \subset [0, 1]$
, for each
![]() $\epsilon \in (0,1)$
we can write
$\epsilon \in (0,1)$
we can write
 $$ \begin{align*} \int_{(0, \infty)} \min\{1, s\} \: \mu_0({\textrm{d}} s) \geq \int_{(\epsilon/2, 1]} s \: \mu_0({\textrm{d}} s); \end{align*} $$
$$ \begin{align*} \int_{(0, \infty)} \min\{1, s\} \: \mu_0({\textrm{d}} s) \geq \int_{(\epsilon/2, 1]} s \: \mu_0({\textrm{d}} s); \end{align*} $$
thus, to conclude (4.53), it is enough to show that
 $$ \begin{align} \int_{(\epsilon/2, 1]} s \: \mu_0({\textrm{d}} s) \gtrsim \log \epsilon^{-1}. \end{align} $$
$$ \begin{align} \int_{(\epsilon/2, 1]} s \: \mu_0({\textrm{d}} s) \gtrsim \log \epsilon^{-1}. \end{align} $$
For the proof, for any
![]() $\epsilon \in (0,1)$
we define the following bounded continuous function:
$\epsilon \in (0,1)$
we define the following bounded continuous function:
 $$ \begin{align} f_{\epsilon}(s) = \begin{cases} 0 & \text{if } s<\epsilon/2,\\ 2s-\epsilon, & \text{if } \epsilon/2 \leq s < \epsilon,\\ s & \text{if } \epsilon \leq s < 1,\\ 1 & \text{if }s \geq 1. \end{cases} \end{align} $$
$$ \begin{align} f_{\epsilon}(s) = \begin{cases} 0 & \text{if } s<\epsilon/2,\\ 2s-\epsilon, & \text{if } \epsilon/2 \leq s < \epsilon,\\ s & \text{if } \epsilon \leq s < 1,\\ 1 & \text{if }s \geq 1. \end{cases} \end{align} $$
We have, in view of (4.52),
 $$ \begin{align} \int_{(\epsilon/2,1]} s \: \mu_0({\textrm{d}}s) \geq \int_{(0,1]}f_{\epsilon}(s) \: \mu_0({\textrm{d}}s) = \lim_{n \to \infty} \int_{(0,1]}f_{\epsilon}(s) \: \mu_{t_n}({\textrm{d}}s) \geq \liminf_{n \to \infty} \int_{(\epsilon,1]} s\:\mu_{t_n}({\textrm{d}}s). \end{align} $$
$$ \begin{align} \int_{(\epsilon/2,1]} s \: \mu_0({\textrm{d}}s) \geq \int_{(0,1]}f_{\epsilon}(s) \: \mu_0({\textrm{d}}s) = \lim_{n \to \infty} \int_{(0,1]}f_{\epsilon}(s) \: \mu_{t_n}({\textrm{d}}s) \geq \liminf_{n \to \infty} \int_{(\epsilon,1]} s\:\mu_{t_n}({\textrm{d}}s). \end{align} $$
Let us estimate the last integral. We write
 $$ \begin{align*} \int_{(\epsilon, 1]} s \: \mu_t (\rm{d} s) \nonumber &= t\lambda^{-1} \int_{(\lambda \epsilon, \lambda]}s \: \nu_1({\textrm{d}}s) \\ &= \tfrac{1}{2} t \lambda^{-1}\int_{(\lambda \epsilon, \lambda ]}s \: \nu({\textrm{d}}s). \end{align*} $$
$$ \begin{align*} \int_{(\epsilon, 1]} s \: \mu_t (\rm{d} s) \nonumber &= t\lambda^{-1} \int_{(\lambda \epsilon, \lambda]}s \: \nu_1({\textrm{d}}s) \\ &= \tfrac{1}{2} t \lambda^{-1}\int_{(\lambda \epsilon, \lambda ]}s \: \nu({\textrm{d}}s). \end{align*} $$
By the Fubini–Tonelli theorem, we get
 $$ \begin{align*} \int_{{(\lambda\epsilon,\lambda]}} s \:\nu({\textrm{d}}s) = \int_{\lambda \epsilon}^{\lambda}u^{-2} \int_{(0,u]} s^2\:\nu({\textrm{d}}s) \:{\textrm{d}}u + \lambda K(\lambda) - \lambda \epsilon K(\lambda \epsilon). \end{align*} $$
$$ \begin{align*} \int_{{(\lambda\epsilon,\lambda]}} s \:\nu({\textrm{d}}s) = \int_{\lambda \epsilon}^{\lambda}u^{-2} \int_{(0,u]} s^2\:\nu({\textrm{d}}s) \:{\textrm{d}}u + \lambda K(\lambda) - \lambda \epsilon K(\lambda \epsilon). \end{align*} $$
Thus,
 $$ \begin{align} 2 \int_{{(\epsilon,1]}} s \:\mu_t({\textrm{d}}s) = t\lambda^{-1} \int_{\lambda \epsilon}^{\lambda} K(u)\:{\textrm{d}}u + tK(\lambda) - t\epsilon K(\lambda \epsilon). \end{align} $$
$$ \begin{align} 2 \int_{{(\epsilon,1]}} s \:\mu_t({\textrm{d}}s) = t\lambda^{-1} \int_{\lambda \epsilon}^{\lambda} K(u)\:{\textrm{d}}u + tK(\lambda) - t\epsilon K(\lambda \epsilon). \end{align} $$
Setting
![]() $z = 1/\lambda $
, by (4.2) and (4.45), we obtain
$z = 1/\lambda $
, by (4.2) and (4.45), we obtain
Moreover, since
![]() $\varphi $
is a
$\varphi $
is a
![]() $1$
-regularly varying function at infinity, we have
$1$
-regularly varying function at infinity, we have
 $$ \begin{align*} t\epsilon K(\lambda \epsilon) \approx t \epsilon \varphi(z/\epsilon) = M \epsilon \frac{\varphi(z/\epsilon)}{\varphi(z)}\to M, \end{align*} $$
$$ \begin{align*} t\epsilon K(\lambda \epsilon) \approx t \epsilon \varphi(z/\epsilon) = M \epsilon \frac{\varphi(z/\epsilon)}{\varphi(z)}\to M, \end{align*} $$
as z tends to infinity. Therefore, it remains to estimate the integral in (4.57). Using (4.2) we get
 $$ \begin{align*} t\lambda^{-1} \int_{\lambda \epsilon}^{\lambda} K(u)\:{\textrm{d}}u &\approx \frac{z}{\varphi(z)} \int_{\epsilon z^{-1}}^{z^{-1}}\varphi \big( u^{-1} \big)\:{\textrm{d}}u \\ &=\frac{z}{\varphi(z)}\int_z^{\epsilon^{-1}z}u^{-2}\varphi(u)\:{\textrm{d}}u \\ &= \frac{\phi'(z)-\phi' \big(\epsilon^{-1}z\big)}{z \big(-\phi^{\prime\prime}(z)\big)}. \end{align*} $$
$$ \begin{align*} t\lambda^{-1} \int_{\lambda \epsilon}^{\lambda} K(u)\:{\textrm{d}}u &\approx \frac{z}{\varphi(z)} \int_{\epsilon z^{-1}}^{z^{-1}}\varphi \big( u^{-1} \big)\:{\textrm{d}}u \\ &=\frac{z}{\varphi(z)}\int_z^{\epsilon^{-1}z}u^{-2}\varphi(u)\:{\textrm{d}}u \\ &= \frac{\phi'(z)-\phi' \big(\epsilon^{-1}z\big)}{z \big(-\phi^{\prime\prime}(z)\big)}. \end{align*} $$
Since
![]() $-\phi ^{\prime \prime }(s)=s^{-1} \ell (s)$
for a certain function
$-\phi ^{\prime \prime }(s)=s^{-1} \ell (s)$
for a certain function
![]() $\ell $
slowly varying at infinity, by [Reference Bingham, Goldie and Teugels3, Theorem 1.5.6],
$\ell $
slowly varying at infinity, by [Reference Bingham, Goldie and Teugels3, Theorem 1.5.6],
 $$ \begin{align*} \frac{\phi'(z)-\phi' \big(\epsilon^{-1}z\big)}{z \big(-\phi^{\prime\prime}(z)\big)} = \int_1^{\epsilon^{-1}} \frac{\ell(zt)}{\ell(z)} \frac{{\textrm{d}}t}{t} \to \log \epsilon^{-1}, \end{align*} $$
$$ \begin{align*} \frac{\phi'(z)-\phi' \big(\epsilon^{-1}z\big)}{z \big(-\phi^{\prime\prime}(z)\big)} = \int_1^{\epsilon^{-1}} \frac{\ell(zt)}{\ell(z)} \frac{{\textrm{d}}t}{t} \to \log \epsilon^{-1}, \end{align*} $$
as z tends to infinity. Hence,
 $$ \begin{align*} \liminf_{n \to \infty} \int_{(\epsilon, 1]} s \: \mu_{t_n}({\textrm{d}} s) \gtrsim \log \epsilon^{-1}, \end{align*} $$
$$ \begin{align*} \liminf_{n \to \infty} \int_{(\epsilon, 1]} s \: \mu_{t_n}({\textrm{d}} s) \gtrsim \log \epsilon^{-1}, \end{align*} $$
which by (4.56) implies (4.54).
Next, let us consider the case (i); that is, when
![]() $-\phi ^{\prime \prime } \in \mathrm {WUSC}(\beta -2,C,x_0)$
with
$-\phi ^{\prime \prime } \in \mathrm {WUSC}(\beta -2,C,x_0)$
with
![]() $C \geq 1$
and
$C \geq 1$
and
![]() $\alpha \leq \beta <1$
. We claim that for all
$\alpha \leq \beta <1$
. We claim that for all
![]() $\epsilon \in (0, 1)$
,
$\epsilon \in (0, 1)$
,
 $$ \begin{align} \int_{(0, \epsilon)} s^2 \: \mu_0({\textrm{d}} s)>0. \end{align} $$
$$ \begin{align} \int_{(0, \epsilon)} s^2 \: \mu_0({\textrm{d}} s)>0. \end{align} $$
To see this, it is enough to show that there is
![]() $C> 0$
such that for all
$C> 0$
such that for all
![]() $\epsilon \in (0, 1]$
and
$\epsilon \in (0, 1]$
and
![]() $t \in (0, 1/\varphi (x_0))$
,
$t \in (0, 1/\varphi (x_0))$
,
 $$ \begin{align} \int_{(0, \epsilon)} s^2 \: \mu_t({\textrm{d}} s) \geq C \epsilon^{2-\alpha}. \end{align} $$
$$ \begin{align} \int_{(0, \epsilon)} s^2 \: \mu_t({\textrm{d}} s) \geq C \epsilon^{2-\alpha}. \end{align} $$
For the proof, we select a continuous function on
![]() $\mathbb {R}$
such that
$\mathbb {R}$
such that
and for each
![]() $\tau> 0$
set
$\tau> 0$
set
Since for
![]() $0 < 2 \tau < \epsilon $
,
$0 < 2 \tau < \epsilon $
,
 $$ \begin{align*} \int_{(0, \infty)} s^2 \big(\eta_\epsilon(s) - \eta_\tau(s)\big) \: \mu_t({\textrm{d}} s) + \int_{(0, 2\tau)} s^2 \eta_\tau(s) \: \mu_t({\textrm{d}} s) &\geq \int_{(0, \epsilon)} s^2 \: \mu_t({\textrm{d}} s), \end{align*} $$
$$ \begin{align*} \int_{(0, \infty)} s^2 \big(\eta_\epsilon(s) - \eta_\tau(s)\big) \: \mu_t({\textrm{d}} s) + \int_{(0, 2\tau)} s^2 \eta_\tau(s) \: \mu_t({\textrm{d}} s) &\geq \int_{(0, \epsilon)} s^2 \: \mu_t({\textrm{d}} s), \end{align*} $$
 $$ \begin{align*} \int_{(0, \infty)} s^2 \big(\eta_\epsilon(s) - \eta_\tau(s)\big) \: \mu_0({\textrm{d}} s) + \limsup_{n \to \infty} \int_{(0, \infty)} s^2 \eta_\tau(s) \: \mu_{t_n}({\textrm{d}} s) \geq C \epsilon^{2-\alpha}. \end{align*} $$
$$ \begin{align*} \int_{(0, \infty)} s^2 \big(\eta_\epsilon(s) - \eta_\tau(s)\big) \: \mu_0({\textrm{d}} s) + \limsup_{n \to \infty} \int_{(0, \infty)} s^2 \eta_\tau(s) \: \mu_{t_n}({\textrm{d}} s) \geq C \epsilon^{2-\alpha}. \end{align*} $$
Since
![]() $Y_{t_n}$
and
$Y_{t_n}$
and
![]() $Y_0$
are purely non-Gaussian, by [Reference Sato47, Theorem 8.7(2)],
$Y_0$
are purely non-Gaussian, by [Reference Sato47, Theorem 8.7(2)],
 $$ \begin{align*} \lim_{\tau \to 0^+} \limsup_{n \to \infty} \int_{(-\tau, \tau)} s^2 \: \mu_{t_n} ({\textrm{d}} s) = 0; \end{align*} $$
$$ \begin{align*} \lim_{\tau \to 0^+} \limsup_{n \to \infty} \int_{(-\tau, \tau)} s^2 \: \mu_{t_n} ({\textrm{d}} s) = 0; \end{align*} $$
thus,
 $$ \begin{align*} \int_{(0, \epsilon)} s^2 \:\mu_0({\textrm{d}} s) \geq C \epsilon^{2-\alpha}, \end{align*} $$
$$ \begin{align*} \int_{(0, \epsilon)} s^2 \:\mu_0({\textrm{d}} s) \geq C \epsilon^{2-\alpha}, \end{align*} $$
which entails (4.58).
We now turn to showing (4.59). We have
 $$ \begin{align*} \int_{(0, \epsilon)} s^2 \: \mu_t({\textrm{d}} s) &= t \lambda^{-2} \int_{(0, \lambda \epsilon)} s^2 \: \nu_1({\textrm{d}} s) \\ &= \tfrac{1}{2} t \lambda^{-2} \int_{(0, \lambda \epsilon)} s^2 \: \nu({\textrm{d}} s)\\ &= \tfrac{1}{2} t \epsilon^2 K(\lambda \epsilon); \end{align*} $$
$$ \begin{align*} \int_{(0, \epsilon)} s^2 \: \mu_t({\textrm{d}} s) &= t \lambda^{-2} \int_{(0, \lambda \epsilon)} s^2 \: \nu_1({\textrm{d}} s) \\ &= \tfrac{1}{2} t \lambda^{-2} \int_{(0, \lambda \epsilon)} s^2 \: \nu({\textrm{d}} s)\\ &= \tfrac{1}{2} t \epsilon^2 K(\lambda \epsilon); \end{align*} $$
thus, by (4.2) and the weak lower scaling property of
![]() $\varphi $
,
$\varphi $
,
 $$ \begin{align*} \int_{(0, \epsilon)} s^2 \:\mu_t({\textrm{d}} s) &\gtrsim t \epsilon^2 \varphi\big(\epsilon^{-1} \lambda^{-1}\big) \\ &\gtrsim t \epsilon^{2-\alpha} \varphi(1/\lambda), \end{align*} $$
$$ \begin{align*} \int_{(0, \epsilon)} s^2 \:\mu_t({\textrm{d}} s) &\gtrsim t \epsilon^2 \varphi\big(\epsilon^{-1} \lambda^{-1}\big) \\ &\gtrsim t \epsilon^{2-\alpha} \varphi(1/\lambda), \end{align*} $$
which, together with the definition of
![]() $\lambda $
, implies (4.59).
$\lambda $
, implies (4.59).
Since the support of the probability distribution of
![]() $Y_0$
is not the whole real line, by [Reference Picard42, Lemma 2.5], the inequality (4.58) implies that
$Y_0$
is not the whole real line, by [Reference Picard42, Lemma 2.5], the inequality (4.58) implies that
 $$ \begin{align} \int_{(0, \infty)} \min\{1, s\} \: \mu_0({\textrm{d}} s) < \infty \end{align} $$
$$ \begin{align} \int_{(0, \infty)} \min\{1, s\} \: \mu_0({\textrm{d}} s) < \infty \end{align} $$
and the support of
![]() $Y_0$
equals
$Y_0$
equals
![]() $[\chi , \infty )$
where
$[\chi , \infty )$
where
 $$ \begin{align} \chi = \gamma_0 - \int_{(0, \infty)} sw(s) \: \mu_0({\textrm{d}} s) = -\int_{(0, 1]} s \: \mu_0({\textrm{d}} s). \end{align} $$
$$ \begin{align} \chi = \gamma_0 - \int_{(0, \infty)} sw(s) \: \mu_0({\textrm{d}} s) = -\int_{(0, 1]} s \: \mu_0({\textrm{d}} s). \end{align} $$
To conclude (4.49), it is enough to show that
![]() $\chi \leq -\tilde {\rho }$
. Since
$\chi \leq -\tilde {\rho }$
. Since
 $\rho (t_n) \leq \frac {1}{2}t_n \lambda _n^{-1} b_{\lambda _n}$
, the latter can be deduced from
$\rho (t_n) \leq \frac {1}{2}t_n \lambda _n^{-1} b_{\lambda _n}$
, the latter can be deduced from
 $$ \begin{align} \begin{aligned} \chi &= -\lim_{n \to \infty} \frac{1}{2} t_n \lambda_n^{-1} b_{\lambda_n} \\ &= -\lim_{n \to \infty} \int_{(0, 1]} s \: \mu_{t_n}({\textrm{d}} s), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \chi &= -\lim_{n \to \infty} \frac{1}{2} t_n \lambda_n^{-1} b_{\lambda_n} \\ &= -\lim_{n \to \infty} \int_{(0, 1]} s \: \mu_{t_n}({\textrm{d}} s), \end{aligned} \end{align} $$
where the last equality is a consequence of (4.48) since
 $$ \begin{align} \int_{(0, 1]} s \: \mu_t (\rm{d} s) &= t\lambda^{-1} \int_{(0, \lambda]} s \: \nu_1({\textrm{d}}s) \nonumber\\ &= \tfrac{1}{2} t \lambda^{-1}\int_{(0, \lambda] }s \: \nu({\textrm{d}}s). \end{align} $$
$$ \begin{align} \int_{(0, 1]} s \: \mu_t (\rm{d} s) &= t\lambda^{-1} \int_{(0, \lambda]} s \: \nu_1({\textrm{d}}s) \nonumber\\ &= \tfrac{1}{2} t \lambda^{-1}\int_{(0, \lambda] }s \: \nu({\textrm{d}}s). \end{align} $$
Therefore, the problem is reduced to showing (4.62). By the monotone convergence theorem and (4.52), we have
 $$ \begin{align} \begin{aligned} \chi &= -\lim_{\epsilon \to 0^+} \int_{(0,1]} f_{\epsilon}(s) \: \mu_0({\textrm{d}}s) \\ &= -\lim_{\epsilon \to 0^+} \lim_{n \to \infty}\int_{(0,1]} f_{\epsilon}(s) \: \mu_{t_n}({\textrm{d}}s) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \chi &= -\lim_{\epsilon \to 0^+} \int_{(0,1]} f_{\epsilon}(s) \: \mu_0({\textrm{d}}s) \\ &= -\lim_{\epsilon \to 0^+} \lim_{n \to \infty}\int_{(0,1]} f_{\epsilon}(s) \: \mu_{t_n}({\textrm{d}}s) \end{aligned} \end{align} $$
and
 $$ \begin{align} \lim_{\epsilon \to 0^+} \int_{(0,1]} f_{\epsilon}(s) \: \mu_{t_n}({\textrm{d}}s) = \int_{(0, 1]} s \: \mu_{t_n}({\textrm{d}} s), \end{align} $$
$$ \begin{align} \lim_{\epsilon \to 0^+} \int_{(0,1]} f_{\epsilon}(s) \: \mu_{t_n}({\textrm{d}}s) = \int_{(0, 1]} s \: \mu_{t_n}({\textrm{d}} s), \end{align} $$
where
![]() $f_{\epsilon }$
is as in (4.55). Hence, we just need to justify the change in the order of limits. In view of the Moore–Osgood theorem [Reference Graves19, Chapter VII], it is enough to show that the limit in (4.65) is uniform with respect to
$f_{\epsilon }$
is as in (4.55). Hence, we just need to justify the change in the order of limits. In view of the Moore–Osgood theorem [Reference Graves19, Chapter VII], it is enough to show that the limit in (4.65) is uniform with respect to
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
We write
 $$ \begin{align*} \bigg| \int_{(0, 1]} s \: \mu_t({\textrm{d}} s) - \int_{(0, 1]} f_\epsilon(s) \: \mu_t({\textrm{d}} s) \bigg| &\leq \int_{(0, \epsilon/2]} s \: \mu_t({\textrm{d}} s) + \int_{(\epsilon/2, \epsilon]} (\epsilon-s) \: \mu_t({\textrm{d}} s) \\ &\leq \int_{(0, \epsilon]} s \: \mu_t({\textrm{d}} s). \end{align*} $$
$$ \begin{align*} \bigg| \int_{(0, 1]} s \: \mu_t({\textrm{d}} s) - \int_{(0, 1]} f_\epsilon(s) \: \mu_t({\textrm{d}} s) \bigg| &\leq \int_{(0, \epsilon/2]} s \: \mu_t({\textrm{d}} s) + \int_{(\epsilon/2, \epsilon]} (\epsilon-s) \: \mu_t({\textrm{d}} s) \\ &\leq \int_{(0, \epsilon]} s \: \mu_t({\textrm{d}} s). \end{align*} $$
By (4.63) and the Fubini–Tonelli theorem, we have
 $$ \begin{align*} 2 t^{-1} \lambda \int_{(0, \epsilon]} s \: \mu_t({\textrm{d}} s) = \int_{(0, \lambda \epsilon]}s \: \nu({\textrm{d}}s) &= \int_0^{\lambda \epsilon} u^{-2} \int_{(0,u]} s^2 \: \nu({\textrm{d}} s) {\: \rm d} u + \lambda \epsilon K (\lambda \epsilon) \\ &\approx \int_0^{\lambda \epsilon} \varphi\big(u^{-1}\big) {\: \rm d} u + \lambda \epsilon \varphi\big(\lambda^{-1}\epsilon^{-1}\big). \end{align*} $$
$$ \begin{align*} 2 t^{-1} \lambda \int_{(0, \epsilon]} s \: \mu_t({\textrm{d}} s) = \int_{(0, \lambda \epsilon]}s \: \nu({\textrm{d}}s) &= \int_0^{\lambda \epsilon} u^{-2} \int_{(0,u]} s^2 \: \nu({\textrm{d}} s) {\: \rm d} u + \lambda \epsilon K (\lambda \epsilon) \\ &\approx \int_0^{\lambda \epsilon} \varphi\big(u^{-1}\big) {\: \rm d} u + \lambda \epsilon \varphi\big(\lambda^{-1}\epsilon^{-1}\big). \end{align*} $$
By almost monotonicity of
![]() $\varphi $
,
$\varphi $
,
 $$ \begin{align} \nonumber \int_{(0, \epsilon]} s \: \mu_t ({\textrm{d}} s) & \approx t \lambda^{-1} \int_0^{\lambda \epsilon} \varphi\big(u^{-1}\big) {\: \rm d} u + t \epsilon \varphi\big(\lambda^{-1}\epsilon^{-1}\big) \\ &\approx t \lambda^{-1} \int_0^{\lambda \epsilon} \varphi\big(u^{-1}\big) {\: \rm d} u. \end{align} $$
$$ \begin{align} \nonumber \int_{(0, \epsilon]} s \: \mu_t ({\textrm{d}} s) & \approx t \lambda^{-1} \int_0^{\lambda \epsilon} \varphi\big(u^{-1}\big) {\: \rm d} u + t \epsilon \varphi\big(\lambda^{-1}\epsilon^{-1}\big) \\ &\approx t \lambda^{-1} \int_0^{\lambda \epsilon} \varphi\big(u^{-1}\big) {\: \rm d} u. \end{align} $$
Now, setting
![]() $z = \varphi ^{-1}(M/t)$
, by (4.45), we get
$z = \varphi ^{-1}(M/t)$
, by (4.45), we get
 $$ \begin{align} \nonumber t \lambda^{-1} \int_0^{\lambda \epsilon} \varphi\big(u^{-1}\big) {\: \rm d} u &= t\varphi^{-1}(M/t) \int_0^{\epsilon/\varphi^{-1}(M/t)} \varphi \big(u^{-1}\big) {\: \rm d} u \\ \nonumber &\approx \frac{z}{\varphi(z)}\int_0^{\epsilon z^{-1}} \varphi \big( u^{-1} \big) {\: \rm d} u \\ \nonumber &= \frac{z}{\varphi(z)}\int_{\epsilon^{-1} z}^{\infty} u^{-2}\varphi(u) {\: \rm d} u \nonumber \\ &= \frac{\phi'\big(\epsilon^{-1} z\big)}{z \big(-\phi^{\prime\prime}(z)\big)}. \end{align} $$
$$ \begin{align} \nonumber t \lambda^{-1} \int_0^{\lambda \epsilon} \varphi\big(u^{-1}\big) {\: \rm d} u &= t\varphi^{-1}(M/t) \int_0^{\epsilon/\varphi^{-1}(M/t)} \varphi \big(u^{-1}\big) {\: \rm d} u \\ \nonumber &\approx \frac{z}{\varphi(z)}\int_0^{\epsilon z^{-1}} \varphi \big( u^{-1} \big) {\: \rm d} u \\ \nonumber &= \frac{z}{\varphi(z)}\int_{\epsilon^{-1} z}^{\infty} u^{-2}\varphi(u) {\: \rm d} u \nonumber \\ &= \frac{\phi'\big(\epsilon^{-1} z\big)}{z \big(-\phi^{\prime\prime}(z)\big)}. \end{align} $$
In view of Proposition 2.4, by the upper scaling of
![]() $-\phi ^{\prime \prime }$
, there is
$-\phi ^{\prime \prime }$
, there is
![]() $c> 0$
such that for all
$c> 0$
such that for all
![]() $z> x_0$
,
$z> x_0$
,
 $$ \begin{align*} \frac{\phi'\big(\epsilon^{-1} z\big)}{z \big(-\phi^{\prime\prime}(z)\big)} \leq c \epsilon^{1-\beta}. \end{align*} $$
$$ \begin{align*} \frac{\phi'\big(\epsilon^{-1} z\big)}{z \big(-\phi^{\prime\prime}(z)\big)} \leq c \epsilon^{1-\beta}. \end{align*} $$
Hence, the limit in (4.65) is uniform with respect to
![]() $n \in \mathbb {N}$
, which justifies (4.62). This completes the proof of (4.49) and the theorem follows.
$n \in \mathbb {N}$
, which justifies (4.62). This completes the proof of (4.49) and the theorem follows.
Theorem 4.13. Let
![]() $\mathbf {T}$
be a subordinator with the Laplace exponent
$\mathbf {T}$
be a subordinator with the Laplace exponent
![]() $\phi $
. Suppose that
$\phi $
. Suppose that
![]() $\phi \in \mathrm {WLSC}(\alpha ,c,x_0) \cap \mathrm {WUSC}(\beta ,C,x_0)$
for some
$\phi \in \mathrm {WLSC}(\alpha ,c,x_0) \cap \mathrm {WUSC}(\beta ,C,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $C \geq 1$
,
$C \geq 1$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $0 < \alpha \leq \beta < 1$
. We also assume that
$0 < \alpha \leq \beta < 1$
. We also assume that
![]() $b=0$
. Then for all
$b=0$
. Then for all
![]() $0<\chi _1<\chi _2$
there is
$0<\chi _1<\chi _2$
there is
![]() $C' \geq 1$
such that for all
$C' \geq 1$
such that for all
![]() $t \in (0, 1/\varphi (x_0))$
and
$t \in (0, 1/\varphi (x_0))$
and
![]() $x> 0$
satisfying
$x> 0$
satisfying
we have
 $$ \begin{align} C^{'-1} \phi^{-1}(1/t) \leq p(t, x) \leq C' \phi^{-1}(1/t). \end{align} $$
$$ \begin{align} C^{'-1} \phi^{-1}(1/t) \leq p(t, x) \leq C' \phi^{-1}(1/t). \end{align} $$
Proof. First let us notice that Corollary 2.7 implies that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0) \cap \mathrm {WUSC}(\beta -2,C,x_0)$
. Therefore, the hypothesis of Theorem 4.11 is satisfied.
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0) \cap \mathrm {WUSC}(\beta -2,C,x_0)$
. Therefore, the hypothesis of Theorem 4.11 is satisfied.
It is enough to show the first inequality in (4.68) since the latter is an easy consequence of (4.28) and Proposition 4.6. For
![]() $t \in (0, 1/\varphi (x_0))$
and
$t \in (0, 1/\varphi (x_0))$
and
![]() $M \geq 1$
, we set
$M \geq 1$
, we set
 $$ \begin{align*} x_t = t \phi' \big( \varphi^{-1}(M/t) \big). \end{align*} $$
$$ \begin{align*} x_t = t \phi' \big( \varphi^{-1}(M/t) \big). \end{align*} $$
By Proposition 4.6, the function
![]() $\varphi ^{-1}$
possesses the weak lower scaling property. Moreover, there is
$\varphi ^{-1}$
possesses the weak lower scaling property. Moreover, there is
![]() $C_1 \geq 1$
such that for all
$C_1 \geq 1$
such that for all
![]() $r> \varphi (x_0)$
,
$r> \varphi (x_0)$
,
Hence, by Proposition 2.4, there is
![]() $C_2 \geq 1$
, such that
$C_2 \geq 1$
, such that
 $$ \begin{align} x_t \leq C_2 M^{1-1/\beta} \frac{1}{\varphi^{-1}(1/t)}. \end{align} $$
$$ \begin{align} x_t \leq C_2 M^{1-1/\beta} \frac{1}{\varphi^{-1}(1/t)}. \end{align} $$
We select
![]() $M \geq 1$
satisfying
$M \geq 1$
satisfying
Let
![]() $\rho _1 = \rho _0/2$
where
$\rho _1 = \rho _0/2$
where
![]() $\rho _0$
is determined in Theorem 4.11. Then, by (4.69) and (4.70), we have
$\rho _0$
is determined in Theorem 4.11. Then, by (4.69) and (4.70), we have
 $$ \begin{align} \nonumber x_t - \frac{\rho_1}{\varphi^{-1}(1/t)} &\leq C_1 C_2 M^{1-1/\beta} \frac{1}{\phi^{-1}(1/t)} \\ &< \frac{\chi_1}{\phi^{-1}(1/t)}. \end{align} $$
$$ \begin{align} \nonumber x_t - \frac{\rho_1}{\varphi^{-1}(1/t)} &\leq C_1 C_2 M^{1-1/\beta} \frac{1}{\phi^{-1}(1/t)} \\ &< \frac{\chi_1}{\phi^{-1}(1/t)}. \end{align} $$
Now set
![]() $\rho _2 = C_1 \chi _2$
. Then, by (4.69), we have
$\rho _2 = C_1 \chi _2$
. Then, by (4.69), we have
 $$ \begin{align} x_t + \frac{\rho_2}{\varphi^{-1}(1/t)}> \frac{\rho_2}{C_1 \phi^{-1}(1/t)} = \frac{\chi_2}{\phi^{-1}(1/t)}. \end{align} $$
$$ \begin{align} x_t + \frac{\rho_2}{\varphi^{-1}(1/t)}> \frac{\rho_2}{C_1 \phi^{-1}(1/t)} = \frac{\chi_2}{\phi^{-1}(1/t)}. \end{align} $$
Putting (4.72) and (4.71) together, we conclude that
 $$ \begin{align*} \bigg[\frac{\chi_1}{\phi^{-1}(1/t)}, \frac{\chi_2}{\phi^{-1}(1/t)} \bigg] \subseteq \left( x_t - \frac{\rho_1}{\varphi^{-1}(1/t)}, x_t + \frac{\rho_2}{\varphi^{-1}(1/t)} \right). \end{align*} $$
$$ \begin{align*} \bigg[\frac{\chi_1}{\phi^{-1}(1/t)}, \frac{\chi_2}{\phi^{-1}(1/t)} \bigg] \subseteq \left( x_t - \frac{\rho_1}{\varphi^{-1}(1/t)}, x_t + \frac{\rho_2}{\varphi^{-1}(1/t)} \right). \end{align*} $$
Therefore, by Theorem 4.11, for all
![]() $t \in (0, 1/\varphi (x_0))$
and
$t \in (0, 1/\varphi (x_0))$
and
![]() $x> 0$
satisfying
$x> 0$
satisfying
we have
In view of (4.69), this completes the proof of the theorem.
Proposition 4.14. Let
![]() $\mathbf {T}$
be a subordinator with the Laplace exponent
$\mathbf {T}$
be a subordinator with the Laplace exponent
![]() $\phi $
. Suppose that
$\phi $
. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
, and assume that one of the following conditions holds true:
$\alpha>0$
, and assume that one of the following conditions holds true:
-
(i)
 $-\phi ^{\prime \prime } \in \mathrm {WUSC}(\beta -2,C,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WUSC}(\beta -2,C,x_0)$
for some
 $C\geq 1$
and
$C\geq 1$
and
 $\alpha \leq \beta <1$
, or
$\alpha \leq \beta <1$
, or -
(ii)
 $-\phi ^{\prime \prime }$
is a function regularly varying at infinity with index
$-\phi ^{\prime \prime }$
is a function regularly varying at infinity with index
 $-1$
. If
$-1$
. If
 $x_0 = 0$
, we also assume that
$x_0 = 0$
, we also assume that
 $-\phi ^{\prime \prime }$
is regularly varying at zero with index
$-\phi ^{\prime \prime }$
is regularly varying at zero with index
 $-1$
.
$-1$
.
We also assume that the Lévy measure
![]() $\nu ({\mathrm {d}} x)$
has an almost monotone density
$\nu ({\mathrm {d}} x)$
has an almost monotone density
![]() $\nu (x)$
. Then the probability distribution of
$\nu (x)$
. Then the probability distribution of
![]() $T_t$
has a density
$T_t$
has a density
![]() $p(t, \: \cdot \:)$
. Moreover, there are
$p(t, \: \cdot \:)$
. Moreover, there are
![]() $M_0>1$
,
$M_0>1$
,
![]() $\rho _0> 0$
and
$\rho _0> 0$
and
![]() $C> 0$
such that for all
$C> 0$
such that for all
![]() $t \in (0, 1/\varphi (x_0))$
and
$t \in (0, 1/\varphi (x_0))$
and
 $$ \begin{align*} x \geq 2t\phi'\big(\varphi^{-1}({M_0}/t) \big) + \frac{2 \rho_0}{\varphi^{-1}(1/t)}, \end{align*} $$
$$ \begin{align*} x \geq 2t\phi'\big(\varphi^{-1}({M_0}/t) \big) + \frac{2 \rho_0}{\varphi^{-1}(1/t)}, \end{align*} $$
we have
Proof. Let
![]() $\lambda> 0$
. We begin by decomposing the Lévy measure
$\lambda> 0$
. We begin by decomposing the Lévy measure
![]() $\nu ({\mathrm {d}} x)$
. Let
$\nu ({\mathrm {d}} x)$
. Let
![]() $\nu _1({\mathrm {d}} x) = \nu _1(x) {\: \rm d} x$
and
$\nu _1({\mathrm {d}} x) = \nu _1(x) {\: \rm d} x$
and
![]() $\nu _2({\mathrm {d}}x) = \nu _2(x) {\: \rm d} x$
where
$\nu _2({\mathrm {d}}x) = \nu _2(x) {\: \rm d} x$
where

For
![]() $u> 0$
, we set
$u> 0$
, we set
 $$ \begin{align*} \phi_1(u) = b u + \int_{(0, \infty)} \big(1-e^{-u s}\big) \: \nu_1({\textrm{d}} s) \qquad\text{and}\qquad \phi_2(u) = \int_{(0, \infty)} \big(1 - e^{-u s}\big) \: \nu_2({\textrm{d}} s). \end{align*} $$
$$ \begin{align*} \phi_1(u) = b u + \int_{(0, \infty)} \big(1-e^{-u s}\big) \: \nu_1({\textrm{d}} s) \qquad\text{and}\qquad \phi_2(u) = \int_{(0, \infty)} \big(1 - e^{-u s}\big) \: \nu_2({\textrm{d}} s). \end{align*} $$
Let
![]() $\mathbf {T}^{(j)}$
be the Lévy process having the Laplace exponent
$\mathbf {T}^{(j)}$
be the Lévy process having the Laplace exponent
![]() $\phi _j$
, for
$\phi _j$
, for
![]() $j \in \{1, 2\}$
. Since
$j \in \{1, 2\}$
. Since
 $\tfrac {1}{2} \nu \leq \nu _1 \leq \nu $
, we have
$\tfrac {1}{2} \nu \leq \nu _1 \leq \nu $
, we have
 $$ \begin{align*} \tfrac{1}{2} \phi \leq \phi_1 \leq \phi, \end{align*} $$
$$ \begin{align*} \tfrac{1}{2} \phi \leq \phi_1 \leq \phi, \end{align*} $$
and for all
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
 $$ \begin{align} \tfrac{1}{2} (-1)^{n+1} \phi^{(n)} \leq (-1)^{n+1} \phi_1^{(n)} \leq (-1)^{n+1} \phi^{(n)}. \end{align} $$
$$ \begin{align} \tfrac{1}{2} (-1)^{n+1} \phi^{(n)} \leq (-1)^{n+1} \phi_1^{(n)} \leq (-1)^{n+1} \phi^{(n)}. \end{align} $$
Thus,
 $$ \begin{align*} \tfrac{1}{2} \varphi \leq \varphi_1 \leq \varphi, \end{align*} $$
$$ \begin{align*} \tfrac{1}{2} \varphi \leq \varphi_1 \leq \varphi, \end{align*} $$
and so for all
![]() $u> 0$
,
$u> 0$
,
In particular,
![]() $-\phi _1^{\prime \prime }$
has the weak lower scaling property. Therefore, by Theorem 3.3,
$-\phi _1^{\prime \prime }$
has the weak lower scaling property. Therefore, by Theorem 3.3,
 $T_t^{(1)}$
and
$T_t^{(1)}$
and
![]() $T_t$
are absolutely continuous. Let us denote by
$T_t$
are absolutely continuous. Let us denote by
![]() $p(t, \:\cdot \:)$
and
$p(t, \:\cdot \:)$
and
![]() $p^{(1)}(t, \:\cdot \:)$
the densities of
$p^{(1)}(t, \:\cdot \:)$
the densities of
![]() $T_t$
and
$T_t$
and
 $T_t^{(1)}$
, respectively. Observe that
$T_t^{(1)}$
, respectively. Observe that
![]() $\mathbf {T}^{(2)}$
is a compound Poisson process with the probability distribution denoted by
$\mathbf {T}^{(2)}$
is a compound Poisson process with the probability distribution denoted by
![]() $P_t({\mathrm {d}} x)$
. By [Reference Sato47, Remark 27.3],
$P_t({\mathrm {d}} x)$
. By [Reference Sato47, Remark 27.3],
 $$ \begin{align} P_t({\textrm{d}} x) \geq t e^{-t\nu_2(\mathbb{R})} \nu_2(x) {\: \rm d} x. \end{align} $$
$$ \begin{align} P_t({\textrm{d}} x) \geq t e^{-t\nu_2(\mathbb{R})} \nu_2(x) {\: \rm d} x. \end{align} $$
We apply Theorem 4.11 to the process
![]() $\mathbf {T}^{(1)}$
. For
$\mathbf {T}^{(1)}$
. For
![]() $t> 0$
, we set
$t> 0$
, we set
 $$ \begin{align*} x_t = t \phi'_1\big(\varphi_1^{-1}({M_0}/t)\big). \end{align*} $$
$$ \begin{align*} x_t = t \phi'_1\big(\varphi_1^{-1}({M_0}/t)\big). \end{align*} $$
Then there are
![]() $C> 0$
and
$C> 0$
and
![]() $\rho _0> 0$
, such that for all
$\rho _0> 0$
, such that for all
![]() $t \in (0, 1/\varphi (x_0))$
and
$t \in (0, 1/\varphi (x_0))$
and
![]() $x \geq 0$
satisfying
$x \geq 0$
satisfying
 $$ \begin{align*} x_t - \frac{\rho_0}{\varphi_1^{-1}(1/t)} \leq x \leq x_t + \frac{\rho_0}{\varphi_1^{-1}(1/t)}, \end{align*} $$
$$ \begin{align*} x_t - \frac{\rho_0}{\varphi_1^{-1}(1/t)} \leq x \leq x_t + \frac{\rho_0}{\varphi_1^{-1}(1/t)}, \end{align*} $$
we have
 $$ \begin{align*} p^{(1)}(t, x) \geq C \varphi_1^{-1}(1/t). \end{align*} $$
$$ \begin{align*} p^{(1)}(t, x) \geq C \varphi_1^{-1}(1/t). \end{align*} $$
Therefore, if
 $$ \begin{align*} \lambda = x_t + \frac{\rho_0}{\varphi_1^{-1}(1/t)}, \end{align*} $$
$$ \begin{align*} \lambda = x_t + \frac{\rho_0}{\varphi_1^{-1}(1/t)}, \end{align*} $$
then
 $$ \begin{align} \int_0^\lambda p^{(1)}(t, x) {\: \rm d} x \gtrsim 1. \end{align} $$
$$ \begin{align} \int_0^\lambda p^{(1)}(t, x) {\: \rm d} x \gtrsim 1. \end{align} $$
Next, if
![]() $\lambda \geq \rho _0/\varphi ^{-1}(1/t)$
, then, by (4.2),
$\lambda \geq \rho _0/\varphi ^{-1}(1/t)$
, then, by (4.2),
 $$ \begin{align} \nonumber t \nu_2(\mathbb{R}) &= \tfrac{1}{2} t \int_\lambda^\infty \: \nu(x) {\: \rm d} x \\ \nonumber &\leq \tfrac{1}{2} t h\big(\rho_0/\varphi^{-1}(1/t)\big) \\ \nonumber &\lesssim t h\big(1/\varphi^{-1}(1/t)\big)\\ &\lesssim 1, \end{align} $$
$$ \begin{align} \nonumber t \nu_2(\mathbb{R}) &= \tfrac{1}{2} t \int_\lambda^\infty \: \nu(x) {\: \rm d} x \\ \nonumber &\leq \tfrac{1}{2} t h\big(\rho_0/\varphi^{-1}(1/t)\big) \\ \nonumber &\lesssim t h\big(1/\varphi^{-1}(1/t)\big)\\ &\lesssim 1, \end{align} $$
where the penultimate inequality follows either by monotonicity of h or by [Reference Grzywny and Szczypkowski23, Lemma 2.1 (4)]. Finally, by (4.75) and (4.77), for
![]() $x \geq 2 \lambda $
we can compute
$x \geq 2 \lambda $
we can compute
 $$ \begin{align*} p(t, x) &= \int_{\mathbb{R}} p^{(1)}(t, x - y) P_t({\textrm{d}} y) \\ &\gtrsim t \int_{\mathbb{R}} p^{(1)}(t, x-y) \nu_2(y) {\: \rm d} y \\ &=\tfrac{1}{2} t \int_\lambda^x p^{(1)}(t, x-y) \nu(y) {\: \rm d} y. \end{align*} $$
$$ \begin{align*} p(t, x) &= \int_{\mathbb{R}} p^{(1)}(t, x - y) P_t({\textrm{d}} y) \\ &\gtrsim t \int_{\mathbb{R}} p^{(1)}(t, x-y) \nu_2(y) {\: \rm d} y \\ &=\tfrac{1}{2} t \int_\lambda^x p^{(1)}(t, x-y) \nu(y) {\: \rm d} y. \end{align*} $$
Hence, by the monotonicity of
![]() $\nu $
, we get
$\nu $
, we get
 $$ \begin{align*} p(t, x) &\gtrsim t \nu(x) \int_0^{x - \lambda} p^{(1)}(t, y) {\: \rm d} y\\ &\geq t \nu(x) \int_0^\lambda p^{(1)}(t, y) {\: \rm d} y \\ &\gtrsim t \nu(x), \end{align*} $$
$$ \begin{align*} p(t, x) &\gtrsim t \nu(x) \int_0^{x - \lambda} p^{(1)}(t, y) {\: \rm d} y\\ &\geq t \nu(x) \int_0^\lambda p^{(1)}(t, y) {\: \rm d} y \\ &\gtrsim t \nu(x), \end{align*} $$
where in the last estimate we have used (4.76). Using (4.73) and (4.74), we can easily show that
 $$ \begin{align*} \lambda = x_t + \frac{\rho_0}{\varphi_1^{-1}(1/t)} \leq t \phi'\big(\varphi^{-1}({M_0}/t)\big) +\frac{\rho_0}{\varphi^{-1}(1/t)}, \end{align*} $$
$$ \begin{align*} \lambda = x_t + \frac{\rho_0}{\varphi_1^{-1}(1/t)} \leq t \phi'\big(\varphi^{-1}({M_0}/t)\big) +\frac{\rho_0}{\varphi^{-1}(1/t)}, \end{align*} $$
and the proposition follows.
4.3. Sharp two-sided estimates
In this section we present sharp two-sided estimates on the density
![]() $p(t, \: \cdot \:)$
assuming both the weak lower and upper scaling properties on
$p(t, \: \cdot \:)$
assuming both the weak lower and upper scaling properties on
![]() $-\phi ^{\prime \prime }$
. First, following [Reference Bogdan, Grzywny and Ryznar6, Lemma 13], we prove an auxiliary result.
$-\phi ^{\prime \prime }$
. First, following [Reference Bogdan, Grzywny and Ryznar6, Lemma 13], we prove an auxiliary result.
Proposition 4.15. Assume that the Lévy measure
![]() $\nu ({\mathrm {d}}x)$
has an almost monotone density
$\nu ({\mathrm {d}}x)$
has an almost monotone density
![]() $\nu (x)$
. Suppose that
$\nu (x)$
. Suppose that
![]() $-\phi ^{\prime \prime } \in \mathrm {WUSC}(\gamma ,C,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WUSC}(\gamma ,C,x_0)$
for some
![]() $C \geq 1$
,
$C \geq 1$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\gamma <0$
. Then there are
$\gamma <0$
. Then there are
![]() $a \in (0,1]$
and
$a \in (0,1]$
and
![]() $c \in (0,1]$
such that for all
$c \in (0,1]$
such that for all
![]() $0 < x < a/x_0$
,
$0 < x < a/x_0$
,
 $$ \begin{align*} \nu(x) \geq c x^{-3} \big( -\phi^{\prime\prime}(1/x) \big). \end{align*} $$
$$ \begin{align*} \nu(x) \geq c x^{-3} \big( -\phi^{\prime\prime}(1/x) \big). \end{align*} $$
Proof. Let
![]() $a \in (0,1]$
. Recall that by (4.30) we have
$a \in (0,1]$
. Recall that by (4.30) we have
 $\nu (s) \leq C_1 s^{-3} \big ( -\phi ^{\prime \prime }(1/s) \big )$
for any
$\nu (s) \leq C_1 s^{-3} \big ( -\phi ^{\prime \prime }(1/s) \big )$
for any
![]() $s>0$
. Hence, for any
$s>0$
. Hence, for any
![]() $u>0$
,
$u>0$
,
 $$ \begin{align} \nonumber -\phi^{\prime\prime}(u) &= \int_0^{au^{-1}} s^2e^{-us} \nu(s) {\: \rm d} s + \int_{au^{-1}}^{\infty} s^2e^{-us} \nu(s) {\: \rm d} s \\ &\leq C_1 \int_0^{au^{-1}} s^{-1}e^{-us} \big( -\phi^{\prime\prime}(1/s) \big) {\: \rm d} s + C_2 \nu(au^{-1}) \int_{au^{-1}}^{\infty} s^2e^{-us} {\: \rm d} s, \end{align} $$
$$ \begin{align} \nonumber -\phi^{\prime\prime}(u) &= \int_0^{au^{-1}} s^2e^{-us} \nu(s) {\: \rm d} s + \int_{au^{-1}}^{\infty} s^2e^{-us} \nu(s) {\: \rm d} s \\ &\leq C_1 \int_0^{au^{-1}} s^{-1}e^{-us} \big( -\phi^{\prime\prime}(1/s) \big) {\: \rm d} s + C_2 \nu(au^{-1}) \int_{au^{-1}}^{\infty} s^2e^{-us} {\: \rm d} s, \end{align} $$
where
![]() $C_2$
is a constant from the almost monotonicity of
$C_2$
is a constant from the almost monotonicity of
![]() $\nu $
. If
$\nu $
. If
![]() $u> x_0$
, then by the scaling property of
$u> x_0$
, then by the scaling property of
![]() $-\phi ^{\prime \prime }$
we obtain
$-\phi ^{\prime \prime }$
we obtain
 $$ \begin{align*} C_1 \int_0^{au^{-1}} s^{-1}e^{-us} \big( -\phi^{\prime\prime}(1/s) \big) {\: \rm d} s &\leq C\int_0^{au^{-1}} s^{-1}e^{-us} (su)^{-\gamma} \big( -\phi^{\prime\prime}(u) \big) {\: \rm d} s \\ &\leq C \big( -\phi^{\prime\prime}(u) \big) \int_0^as^{-1-\gamma} e^{-s} {\: \rm d} s. \end{align*} $$
$$ \begin{align*} C_1 \int_0^{au^{-1}} s^{-1}e^{-us} \big( -\phi^{\prime\prime}(1/s) \big) {\: \rm d} s &\leq C\int_0^{au^{-1}} s^{-1}e^{-us} (su)^{-\gamma} \big( -\phi^{\prime\prime}(u) \big) {\: \rm d} s \\ &\leq C \big( -\phi^{\prime\prime}(u) \big) \int_0^as^{-1-\gamma} e^{-s} {\: \rm d} s. \end{align*} $$
By selecting
![]() $a \in (0, 1]$
such that
$a \in (0, 1]$
such that
 $$ \begin{align*} 2C \int_0^a s^{-1-\gamma}e^{-s} {\: \rm d} s \leq 1, \end{align*} $$
$$ \begin{align*} 2C \int_0^a s^{-1-\gamma}e^{-s} {\: \rm d} s \leq 1, \end{align*} $$
we get
 $$ \begin{align*} \int_0^{au^{-1}} s^{-1}e^{-us} \big( -\phi^{\prime\prime}(1/s) \big) {\: \rm d} s \leq \tfrac{1}{2} \big( -\phi^{\prime\prime}(u) \big). \end{align*} $$
$$ \begin{align*} \int_0^{au^{-1}} s^{-1}e^{-us} \big( -\phi^{\prime\prime}(1/s) \big) {\: \rm d} s \leq \tfrac{1}{2} \big( -\phi^{\prime\prime}(u) \big). \end{align*} $$
Since
 $$ \begin{align*} \int_{au^{-1}}^{\infty} s^2 e^{-us} {\: \rm d} s = u^{-3} e^{-a}(a^2+2a+2), \end{align*} $$
$$ \begin{align*} \int_{au^{-1}}^{\infty} s^2 e^{-us} {\: \rm d} s = u^{-3} e^{-a}(a^2+2a+2), \end{align*} $$
by (4.78) we obtain
 $$ \begin{align*} \nu(au^{-1}) \geq \frac{e^a}{2(a^2+2a+2)}u^3 \big( -\phi^{\prime\prime}(u) \big), \end{align*} $$
$$ \begin{align*} \nu(au^{-1}) \geq \frac{e^a}{2(a^2+2a+2)}u^3 \big( -\phi^{\prime\prime}(u) \big), \end{align*} $$
provided that
![]() $u> x_0$
. Now, by the monotonicity of
$u> x_0$
. Now, by the monotonicity of
![]() $-\phi ^{\prime \prime }$
we conclude the proof.
$-\phi ^{\prime \prime }$
we conclude the proof.
In view of Propositions 2.3 and 2.4, we immediately obtain the following corollary.
Corollary 4.16. Assume that the Lévy measure
![]() $\nu ({\mathrm {d}}x)$
has an almost monotone density
$\nu ({\mathrm {d}}x)$
has an almost monotone density
![]() $\nu (x)$
. Suppose that
$\nu (x)$
. Suppose that
![]() $b=0$
and
$b=0$
and
![]() $\phi \in \mathrm {WLSC}(\alpha ,c,x_0) \cap \mathrm {WUSC}(\beta ,C,x_0)$
for some
$\phi \in \mathrm {WLSC}(\alpha ,c,x_0) \cap \mathrm {WUSC}(\beta ,C,x_0)$
for some
![]() $c \in (0,1]$
,
$c \in (0,1]$
,
![]() $C \geq 1$
,
$C \geq 1$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $0<\alpha \leq \beta < 1$
. Then there are
$0<\alpha \leq \beta < 1$
. Then there are
![]() $a \in (0,1]$
and
$a \in (0,1]$
and
![]() $c' \in (0,1]$
such that for all
$c' \in (0,1]$
such that for all
![]() $0 < x<a/x_0$
,
$0 < x<a/x_0$
,
We are now ready to prove our main result in this section.
Theorem 4.17. Let
![]() $\mathbf {T}$
be a subordinator with the Laplace exponent
$\mathbf {T}$
be a subordinator with the Laplace exponent
![]() $\phi $
. Suppose that
$\phi $
. Suppose that
![]() $\phi \in \mathrm {WLSC}(\alpha ,c,x_0) \cap \mathrm {WUSC}(\beta ,C,x_0)$
for some
$\phi \in \mathrm {WLSC}(\alpha ,c,x_0) \cap \mathrm {WUSC}(\beta ,C,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $C \geq 1$
,
$C \geq 1$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $0 < \alpha \leq \beta < 1$
. We also assume that
$0 < \alpha \leq \beta < 1$
. We also assume that
![]() $b=0$
and that the Lévy measure
$b=0$
and that the Lévy measure
![]() $\nu ({\mathrm {d}} x)$
has an almost monotone density
$\nu ({\mathrm {d}} x)$
has an almost monotone density
![]() $\nu (x)$
. Then there is
$\nu (x)$
. Then there is
![]() $x_1 \in (0, \infty ]$
such that for all
$x_1 \in (0, \infty ]$
such that for all
![]() $t \in (0, 1/\varphi (x_0))$
and
$t \in (0, 1/\varphi (x_0))$
and
![]() $x \in (0,x_1)$
,
$x \in (0,x_1)$
,
 $$ \begin{align*} p(t, x) \approx \begin{cases} \big(t (-\phi^{\prime\prime}(w)) \big)^{-\frac{1}{2}} \exp\big\{-t \big(\phi(w) - w \phi'(w)\big) \big\} &\quad \text{if } 0 < x \phi^{-1}(1/t) \leq 1, \\ t x^{-1}\phi(1/x) & \quad\text{if } 1 < x \phi^{-1}(1/t), \end{cases} \end{align*} $$
$$ \begin{align*} p(t, x) \approx \begin{cases} \big(t (-\phi^{\prime\prime}(w)) \big)^{-\frac{1}{2}} \exp\big\{-t \big(\phi(w) - w \phi'(w)\big) \big\} &\quad \text{if } 0 < x \phi^{-1}(1/t) \leq 1, \\ t x^{-1}\phi(1/x) & \quad\text{if } 1 < x \phi^{-1}(1/t), \end{cases} \end{align*} $$
where
![]() $w = (\phi ')^{-1}(x/t)$
. If
$w = (\phi ')^{-1}(x/t)$
. If
![]() $x_0 = 0$
then
$x_0 = 0$
then
![]() $x_1 = \infty $
.
$x_1 = \infty $
.
Proof. First let us note that by Corollary 2.7,
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0) \cap \mathrm {WUSC}(\beta -2,C,x_0)$
. Therefore, we are in position to apply Proposition 4.14. By Corollary 3.7, for
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0) \cap \mathrm {WUSC}(\beta -2,C,x_0)$
. Therefore, we are in position to apply Proposition 4.14. By Corollary 3.7, for
![]() $\chi _1 = \min {\{1, \delta \}}$
, we have
$\chi _1 = \min {\{1, \delta \}}$
, we have
 $$ \begin{align*} p(t, x) \approx \big(t (-\phi^{\prime\prime}(w)) \big)^{-\frac{1}{2}} \exp\big\{-t \big(\phi(w) - w \phi'(w)\big) \big\}, \end{align*} $$
$$ \begin{align*} p(t, x) \approx \big(t (-\phi^{\prime\prime}(w)) \big)^{-\frac{1}{2}} \exp\big\{-t \big(\phi(w) - w \phi'(w)\big) \big\}, \end{align*} $$
whenever
![]() $0 < x \phi ^{-1}(1/t) \leq \chi _1$
. Next, let
$0 < x \phi ^{-1}(1/t) \leq \chi _1$
. Next, let
![]() $M_0'$
be
$M_0'$
be
![]() $M_0$
determined by Proposition 4.14. By Proposition 2.4, (4.2) and monotonicity of
$M_0$
determined by Proposition 4.14. By Proposition 2.4, (4.2) and monotonicity of
![]() $\varphi ^{-1}$
, for
$\varphi ^{-1}$
, for
![]() $t \in (0, 1/\varphi (x_0))$
, we get
$t \in (0, 1/\varphi (x_0))$
, we get
 $$ \begin{align*} t \phi'\big(\psi^{-1}(1/t)\big) \lesssim \frac{1}{\psi^{-1}(1/t)} {\qquad \text{and} \qquad t\phi'\big(\varphi^{-1}(M_0'/t)\big) \lesssim \frac{1}{\varphi^{-1}(1/t)};} \end{align*} $$
$$ \begin{align*} t \phi'\big(\psi^{-1}(1/t)\big) \lesssim \frac{1}{\psi^{-1}(1/t)} {\qquad \text{and} \qquad t\phi'\big(\varphi^{-1}(M_0'/t)\big) \lesssim \frac{1}{\varphi^{-1}(1/t)};} \end{align*} $$
thus, by Propositions 4.3 and 4.6, there is
![]() $C_1> 0$
such that
$C_1> 0$
such that
 $$ \begin{align*} 2 e t \phi'\big(\psi^{-1}(1/t)\big) \leq C_1 \frac{1}{\phi^{-1}(1/t)} \end{align*} $$
$$ \begin{align*} 2 e t \phi'\big(\psi^{-1}(1/t)\big) \leq C_1 \frac{1}{\phi^{-1}(1/t)} \end{align*} $$
and
 $$ \begin{align*} 2t\phi' \big(\varphi^{-1}(M_0'/t)\big)+ \frac{2 \rho'_0}{\varphi^{-1}(1/t)} \leq C_1 \frac{1}{\phi^{-1}(1/t)} \end{align*} $$
$$ \begin{align*} 2t\phi' \big(\varphi^{-1}(M_0'/t)\big)+ \frac{2 \rho'_0}{\varphi^{-1}(1/t)} \leq C_1 \frac{1}{\phi^{-1}(1/t)} \end{align*} $$
where
![]() $\rho _0'$
is the value of
$\rho _0'$
is the value of
![]() $\rho _0$
determined in Proposition 4.14. Let
$\rho _0$
determined in Proposition 4.14. Let
![]() $\chi _2 = \max {\{1, C_1, \chi _1\}}$
. By Proposition 4.14 and Corollary 4.16, there is
$\chi _2 = \max {\{1, C_1, \chi _1\}}$
. By Proposition 4.14 and Corollary 4.16, there is
![]() $a \in (0,1]$
such that if
$a \in (0,1]$
such that if
![]() $x \phi ^{-1}(1/t)> \chi _2$
and
$x \phi ^{-1}(1/t)> \chi _2$
and
![]() $0 < x< a/x_0$
, then
$0 < x< a/x_0$
, then
 $$ \begin{align*} p(t, x) &\gtrsim t \nu(x) \\ &\gtrsim tx^{-1}\phi(1/x). \end{align*} $$
$$ \begin{align*} p(t, x) &\gtrsim t \nu(x) \\ &\gtrsim tx^{-1}\phi(1/x). \end{align*} $$
Furthermore, by (4.29), if
![]() $x \phi ^{-1}(1/t)> \chi _2$
, then
$x \phi ^{-1}(1/t)> \chi _2$
, then
 $$ \begin{align*} p(t,x) &\lesssim t\eta (x) \\ &\lesssim tx^{-1}\phi(1/x), \end{align*} $$
$$ \begin{align*} p(t,x) &\lesssim t\eta (x) \\ &\lesssim tx^{-1}\phi(1/x), \end{align*} $$
where in the last step we have also used (4.13). Lastly, by Theorem 4.13 there is
![]() $C_2 \geq 1$
such that for all
$C_2 \geq 1$
such that for all
![]() $t \in (0, 1/\varphi (x_0))$
and
$t \in (0, 1/\varphi (x_0))$
and
![]() $x> 0$
satisfying
$x> 0$
satisfying
we have
We next claim that the following holds true.
Claim 4.18. There exist
![]() $0< c_1 \leq 1 \leq c_2$
such that for all
$0< c_1 \leq 1 \leq c_2$
such that for all
![]() $t \in (0,c_1/\varphi (x_0))$
and
$t \in (0,c_1/\varphi (x_0))$
and
![]() $x>0$
satisfying
$x>0$
satisfying
we have
 $$ \begin{align} t\phi' \big( \phi^{-1}(c_2/t) \big) \leq x \leq t \phi' \big( \phi^{-1}(c_1/t) \big). \end{align} $$
$$ \begin{align} t\phi' \big( \phi^{-1}(c_2/t) \big) \leq x \leq t \phi' \big( \phi^{-1}(c_1/t) \big). \end{align} $$
By Proposition 4.6, there is
![]() $C_3 \geq 1$
such that for
$C_3 \geq 1$
such that for
![]() $r> \varphi (x_0)$
,
$r> \varphi (x_0)$
,
 $$ \begin{align*} C_3^{-1} \varphi^{-1}(r) \leq \phi^{-1}(r) \leq C_3 \varphi^{-1}(r). \end{align*} $$
$$ \begin{align*} C_3^{-1} \varphi^{-1}(r) \leq \phi^{-1}(r) \leq C_3 \varphi^{-1}(r). \end{align*} $$
Let
 $c_2 = (\chi _1 c' C_3^{-2})^{-\beta /(1-\beta )} \in [1, \infty )$
, where
$c_2 = (\chi _1 c' C_3^{-2})^{-\beta /(1-\beta )} \in [1, \infty )$
, where
![]() $c'$
is taken from (4.15). Then
$c'$
is taken from (4.15). Then
 $$ \begin{align*} c_2^{-1} \phi^{-1}(c_2/t) \geq C_3^{-2} c' c_2^{-1+1/\beta} \phi^{-1}(1/t) = \chi_1^{-1} \phi^{-1}(1/t). \end{align*} $$
$$ \begin{align*} c_2^{-1} \phi^{-1}(c_2/t) \geq C_3^{-2} c' c_2^{-1+1/\beta} \phi^{-1}(1/t) = \chi_1^{-1} \phi^{-1}(1/t). \end{align*} $$
Consequently, by Proposition 2.3,
 $$ \begin{align} \nonumber x \geq \frac{\chi_1}{\phi^{-1}(1/t)} &\geq t \frac{\phi \big( \phi^{-1} ( c_2/t) \big)}{\phi^{-1} (c_2/t)} \\ &\geq t \phi' \big( \phi^{-1}(c_2/t) \big). \end{align} $$
$$ \begin{align} \nonumber x \geq \frac{\chi_1}{\phi^{-1}(1/t)} &\geq t \frac{\phi \big( \phi^{-1} ( c_2/t) \big)}{\phi^{-1} (c_2/t)} \\ &\geq t \phi' \big( \phi^{-1}(c_2/t) \big). \end{align} $$
Moreover, there is
![]() $C_4 \geq 1$
such that
$C_4 \geq 1$
such that
![]() $C_4 x\phi '(x) \geq \phi (x)$
provided that
$C_4 x\phi '(x) \geq \phi (x)$
provided that
![]() $x> x_0$
. Therefore, if
$x> x_0$
. Therefore, if
![]() $\chi _2 \leq C_4^{-1}$
, then
$\chi _2 \leq C_4^{-1}$
, then
 $$ \begin{align} \nonumber \frac{\chi_2}{\phi^{-1}(1/t)} &= \chi_2 t \frac{\phi\big(\phi^{-1}(1/t)\big)}{\phi^{-1}(1/t)} \\ &\leq t \phi'\big( \phi^{-1}(1/t) \big), \end{align} $$
$$ \begin{align} \nonumber \frac{\chi_2}{\phi^{-1}(1/t)} &= \chi_2 t \frac{\phi\big(\phi^{-1}(1/t)\big)}{\phi^{-1}(1/t)} \\ &\leq t \phi'\big( \phi^{-1}(1/t) \big), \end{align} $$
which yields (4.80) with
![]() $c_1 = 1$
. Otherwise, if
$c_1 = 1$
. Otherwise, if
![]() $\chi _2> C_4^{-1}$
, then we set
$\chi _2> C_4^{-1}$
, then we set
 $c_1 =\big (C_4 \chi _2 C_3^2 (c')^{-1}\big )^{-\beta /(1-\beta )} \in (0,1]$
. Hence, by Proposition 4.6, for all
$c_1 =\big (C_4 \chi _2 C_3^2 (c')^{-1}\big )^{-\beta /(1-\beta )} \in (0,1]$
. Hence, by Proposition 4.6, for all
![]() $t \in (0,c_1/\varphi (x_0))$
,
$t \in (0,c_1/\varphi (x_0))$
,
 $$ \begin{align*} \frac{C_4 \chi_2}{c_1} \phi^{-1}(c_1/t) \leq C_4 \chi_2 C_3^2 (c')^{-1} c_1^{-1+1/\beta} \phi^{-1}(1/t) = \phi^{-1}(1/t). \end{align*} $$
$$ \begin{align*} \frac{C_4 \chi_2}{c_1} \phi^{-1}(c_1/t) \leq C_4 \chi_2 C_3^2 (c')^{-1} c_1^{-1+1/\beta} \phi^{-1}(1/t) = \phi^{-1}(1/t). \end{align*} $$
Therefore,
 $$ \begin{align*} x &\leq \frac{\chi_2}{\phi^{-1}(1/t)} \\ &\leq t \frac{\chi_2}{c_1} \cdot \frac{\phi^{-1}(c_1/t)}{\phi^{-1}(1/t)} \cdot \frac{\phi \big( \phi^{-1}(c_1/t) \big)}{\phi^{-1}(c_1/t)} \\ &\leq t\phi' \big( \phi^{-1}(c_1/t) \big), \end{align*} $$
$$ \begin{align*} x &\leq \frac{\chi_2}{\phi^{-1}(1/t)} \\ &\leq t \frac{\chi_2}{c_1} \cdot \frac{\phi^{-1}(c_1/t)}{\phi^{-1}(1/t)} \cdot \frac{\phi \big( \phi^{-1}(c_1/t) \big)}{\phi^{-1}(c_1/t)} \\ &\leq t\phi' \big( \phi^{-1}(c_1/t) \big), \end{align*} $$
which, combined with (4.81) and (4.82), implies (4.80).
Now, using Claim 4.18 and Propositions 4.3 and 4.6, we deduce that for
![]() $t \in (0,c_1/\varphi (x_0))$
and
$t \in (0,c_1/\varphi (x_0))$
and
![]() $\chi _1 \leq x \phi ^{-1}(1/t) \leq \chi _2$
,
$\chi _1 \leq x \phi ^{-1}(1/t) \leq \chi _2$
,
and
Hence,
![]() $tw\phi '(w) \approx 1$
and
$tw\phi '(w) \approx 1$
and
 $$ \begin{align} \exp\big\{-t \big(\phi(w) - w \phi'(w)\big) \big\} \approx 1. \end{align} $$
$$ \begin{align} \exp\big\{-t \big(\phi(w) - w \phi'(w)\big) \big\} \approx 1. \end{align} $$
Next, by Propositions 2.4 and 2.1,
 $$ \begin{align*} w^2 \big( -\phi^{\prime\prime}(w) \big) \approx w\phi'(w); \end{align*} $$
$$ \begin{align*} w^2 \big( -\phi^{\prime\prime}(w) \big) \approx w\phi'(w); \end{align*} $$
thus, by (4.83) and (4.84), we obtain
 $$ \begin{align*} \frac{1}{\sqrt{t\big( -\phi^{\prime\prime}(w) \big)}} \approx \frac{w}{\sqrt{tw\phi'(w)}} \approx \phi^{-1}(1/t), \end{align*} $$
$$ \begin{align*} \frac{1}{\sqrt{t\big( -\phi^{\prime\prime}(w) \big)}} \approx \frac{w}{\sqrt{tw\phi'(w)}} \approx \phi^{-1}(1/t), \end{align*} $$
which, together with (4.85), implies that
 $$ \begin{align*} \big(t (-\phi^{\prime\prime}(w)) \big)^{-\frac{1}{2}} \exp\big\{-t \big(\phi(w) - w \phi'(w)\big) \big\} \approx \phi^{-1}(1/t), \end{align*} $$
$$ \begin{align*} \big(t (-\phi^{\prime\prime}(w)) \big)^{-\frac{1}{2}} \exp\big\{-t \big(\phi(w) - w \phi'(w)\big) \big\} \approx \phi^{-1}(1/t), \end{align*} $$
for
![]() $t \in (0,c_1/\varphi (x_0))$
and
$t \in (0,c_1/\varphi (x_0))$
and
![]() $\chi _1 \leq x\phi ^{-1}(1/t) \leq \chi _2$
. In view of (4.79), the theorem follows in the case
$\chi _1 \leq x\phi ^{-1}(1/t) \leq \chi _2$
. In view of (4.79), the theorem follows in the case
![]() $x_0=0$
. Now, it remains to observe that in the case
$x_0=0$
. Now, it remains to observe that in the case
![]() $x_0>0$
we may use positivity and continuity to conclude the claim for all
$x_0>0$
we may use positivity and continuity to conclude the claim for all
![]() $t \in (0,1/\varphi (x_0))$
.
$t \in (0,1/\varphi (x_0))$
.
5. Applications
5.1. Subordination
Let
![]() $(\mathscr {X}, \tau )$
be a locally compact separable metric space with a Radon measure
$(\mathscr {X}, \tau )$
be a locally compact separable metric space with a Radon measure
![]() $\mu $
having full support on
$\mu $
having full support on
![]() $\mathscr {X}$
. Assume that
$\mathscr {X}$
. Assume that
![]() $(X_t \colon t \geq 0)$
is a homogeneous in time Markov process on
$(X_t \colon t \geq 0)$
is a homogeneous in time Markov process on
![]() $\mathscr {X}$
with density
$\mathscr {X}$
with density
![]() $h(t, \: \cdot \:,\: \cdot \:)$
; that is,
$h(t, \: \cdot \:,\: \cdot \:)$
; that is,
 $$ \begin{align*} \mathbb{P}\left(\left. X_t \in B \right| X_0 = x\right) = \int_B h(t, x, y) \: \mu({\textrm{d}} y) \end{align*} $$
$$ \begin{align*} \mathbb{P}\left(\left. X_t \in B \right| X_0 = x\right) = \int_B h(t, x, y) \: \mu({\textrm{d}} y) \end{align*} $$
for any Borel set
![]() $B \subset \mathscr {X}$
,
$B \subset \mathscr {X}$
,
![]() $x \in \mathscr {X}$
and
$x \in \mathscr {X}$
and
![]() $t> 0$
. Assume that for all
$t> 0$
. Assume that for all
![]() $t> 0$
and
$t> 0$
and
![]() $x, y \in \mathscr {X}$
,
$x, y \in \mathscr {X}$
,
 $$ \begin{align} t^{-\frac{n}{\gamma}} \Phi_1\Big(\tau(x, y) t^{-\frac{1}{\gamma}} \Big) \leq h(t, x, y) \leq t^{-\frac{n}{\gamma}} \Phi_2\Big(\tau(x, y) t^{-\frac{1}{\gamma}} \Big) \end{align} $$
$$ \begin{align} t^{-\frac{n}{\gamma}} \Phi_1\Big(\tau(x, y) t^{-\frac{1}{\gamma}} \Big) \leq h(t, x, y) \leq t^{-\frac{n}{\gamma}} \Phi_2\Big(\tau(x, y) t^{-\frac{1}{\gamma}} \Big) \end{align} $$
where n and
![]() $\gamma $
are some positive constants,
$\gamma $
are some positive constants,
![]() $\Phi _1$
and
$\Phi _1$
and
![]() $\Phi _2$
are nonnegative nonincreasing function on
$\Phi _2$
are nonnegative nonincreasing function on
![]() $[0, \infty )$
such that
$[0, \infty )$
such that
![]() $\Phi _1(1)> 0$
and
$\Phi _1(1)> 0$
and
 $$ \begin{align} \mathop{\mathrm{sup}}\limits_{s \geq 0}{\Phi_2(s) (1+s)^{n + \gamma}} < \infty. \end{align} $$
$$ \begin{align} \mathop{\mathrm{sup}}\limits_{s \geq 0}{\Phi_2(s) (1+s)^{n + \gamma}} < \infty. \end{align} $$
By
![]() $H(t, x, y)$
we denote the heat kernel for the subordinate process
$H(t, x, y)$
we denote the heat kernel for the subordinate process
![]() $\left (X_{T_t} \colon t \geq 0\right )$
; that is,
$\left (X_{T_t} \colon t \geq 0\right )$
; that is,
 $$ \begin{align*} H(t, x, y) = \int_0^\infty h(s, x, y) G(t, {\textrm{d}} s), \end{align*} $$
$$ \begin{align*} H(t, x, y) = \int_0^\infty h(s, x, y) G(t, {\textrm{d}} s), \end{align*} $$
where
 $$ \begin{align*} G(t, s) = \mathbb{P}\big(T_t \geq s \big). \end{align*} $$
$$ \begin{align*} G(t, s) = \mathbb{P}\big(T_t \geq s \big). \end{align*} $$
Suppose that
![]() $\phi \in \mathrm {WLSC}(\alpha ,c,x_0) \cap \mathrm {WUSC}(\beta ,C,x_0)$
for some
$\phi \in \mathrm {WLSC}(\alpha ,c,x_0) \cap \mathrm {WUSC}(\beta ,C,x_0)$
for some
![]() $c \in (0, 1]$
,
$c \in (0, 1]$
,
![]() $C \geq 1$
,
$C \geq 1$
,
![]() $x_0> 0$
and
$x_0> 0$
and
![]() $0 < \alpha \leq \beta < 1$
. We also assume that
$0 < \alpha \leq \beta < 1$
. We also assume that
 $$ \begin{align*} \lim_{x \to \infty} \phi'(x) = b = 0 \end{align*} $$
$$ \begin{align*} \lim_{x \to \infty} \phi'(x) = b = 0 \end{align*} $$
and that the Lévy measure
![]() $\nu ({\mathrm {d}} x)$
has an almost monotone density
$\nu ({\mathrm {d}} x)$
has an almost monotone density
![]() $\nu (x)$
.
$\nu (x)$
.
Claim 5.1. For all
![]() $x, y \in \mathscr {X}$
satisfying
$x, y \in \mathscr {X}$
satisfying
![]() $\tau (x, y)^{-\gamma }> x_0$
and any
$\tau (x, y)^{-\gamma }> x_0$
and any
![]() $t \in (0, 1/\varphi (x_0))$
,
$t \in (0, 1/\varphi (x_0))$
,
 $$ \begin{align*} H(t, x, y) \approx \begin{cases} t \phi\big(\tau(x,y)^{-\gamma} \big) \tau(x, y)^{-n} & \textit{if } 0 < t \phi\big(\tau(x, y)^{-\gamma}\big) \leq 1, \\ \big(\phi^{-1}(1/t) \big)^{\frac{n}{\gamma}} & \textit{if } 1 \leq t \phi\big(\tau(x, y)^{-\gamma}\big). \end{cases} \end{align*} $$
$$ \begin{align*} H(t, x, y) \approx \begin{cases} t \phi\big(\tau(x,y)^{-\gamma} \big) \tau(x, y)^{-n} & \textit{if } 0 < t \phi\big(\tau(x, y)^{-\gamma}\big) \leq 1, \\ \big(\phi^{-1}(1/t) \big)^{\frac{n}{\gamma}} & \textit{if } 1 \leq t \phi\big(\tau(x, y)^{-\gamma}\big). \end{cases} \end{align*} $$
By Proposition 2.3,
![]() $\phi ' \in \mathrm {WLSC}(\alpha -1,c,x_0) \cap \mathrm {WUSC}(\beta -1,C,x_0)$
. Let
$\phi ' \in \mathrm {WLSC}(\alpha -1,c,x_0) \cap \mathrm {WUSC}(\beta -1,C,x_0)$
. Let
![]() $0 < r < \phi '(x_0^+)$
. If
$0 < r < \phi '(x_0^+)$
. If
![]() $0 < \lambda \leq C$
, then by setting
$0 < \lambda \leq C$
, then by setting
 $$ \begin{align*} D = C^{\frac{1}{1-\beta}} \lambda^{-\frac{1}{1-\beta}}, \end{align*} $$
$$ \begin{align*} D = C^{\frac{1}{1-\beta}} \lambda^{-\frac{1}{1-\beta}}, \end{align*} $$
the weak upper scaling property of
![]() $\phi '$
implies that
$\phi '$
implies that
 $$ \begin{align*} \lambda r = \lambda \phi'\big((\phi')^{-1} (r)\big) \geq \phi'\big(D (\phi')^{-1} (r) \big). \end{align*} $$
$$ \begin{align*} \lambda r = \lambda \phi'\big((\phi')^{-1} (r)\big) \geq \phi'\big(D (\phi')^{-1} (r) \big). \end{align*} $$
Therefore,
 $$ \begin{align} (\phi')^{-1}(\lambda r) \leq C^{\frac{1}{1-\beta}} \lambda^{-\frac{1}{1-\beta}} (\phi')^{-1}(r). \end{align} $$
$$ \begin{align} (\phi')^{-1}(\lambda r) \leq C^{\frac{1}{1-\beta}} \lambda^{-\frac{1}{1-\beta}} (\phi')^{-1}(r). \end{align} $$
Analogously, we can prove the lower estimate: If
![]() $0 < \lambda \leq c$
, then by setting
$0 < \lambda \leq c$
, then by setting
 $$ \begin{align*} D = c^{\frac{1}{1-\alpha}} \lambda^{-\frac{1}{1-\alpha}}, \end{align*} $$
$$ \begin{align*} D = c^{\frac{1}{1-\alpha}} \lambda^{-\frac{1}{1-\alpha}}, \end{align*} $$
we obtain
 $$ \begin{align*} \lambda r = \lambda \phi'\big((\phi')^{-1} (r)\big) \leq \phi'\big(D (\phi')^{-1} (r) \big) \end{align*} $$
$$ \begin{align*} \lambda r = \lambda \phi'\big((\phi')^{-1} (r)\big) \leq \phi'\big(D (\phi')^{-1} (r) \big) \end{align*} $$
and, consequently,
 $$ \begin{align} (\phi')^{-1}(\lambda r) \geq c^{\frac{1}{1-\alpha}} \lambda^{-\frac{1}{1-\alpha}} (\phi')^{-1}(r). \end{align} $$
$$ \begin{align} (\phi')^{-1}(\lambda r) \geq c^{\frac{1}{1-\alpha}} \lambda^{-\frac{1}{1-\alpha}} (\phi')^{-1}(r). \end{align} $$
Since
![]() $(\phi ')^{-1}$
is nonincreasing, the last inequality is valid for all
$(\phi ')^{-1}$
is nonincreasing, the last inequality is valid for all
![]() $0 < \lambda \leq 1$
. Let
$0 < \lambda \leq 1$
. Let
 $$ \begin{align*} H(t, x, y) &= \left( \int_0^{\frac{1}{\phi^{-1}(1/t)}} + \int_{\frac{1}{\phi^{{-1}(1/t)}}}^\infty \right) h(s, x, y) G(t, {\textrm{d}} s) \\ &= I_1(t, x, y) + I_2(t, x, y). \end{align*} $$
$$ \begin{align*} H(t, x, y) &= \left( \int_0^{\frac{1}{\phi^{-1}(1/t)}} + \int_{\frac{1}{\phi^{{-1}(1/t)}}}^\infty \right) h(s, x, y) G(t, {\textrm{d}} s) \\ &= I_1(t, x, y) + I_2(t, x, y). \end{align*} $$
By Theorem 4.17,
 $$ \begin{align} I_1 \approx \frac{1}{\phi^{-1}(1/t)} \int_0^{1} h\bigg(\frac{u}{\phi^{-1}(1/t)}, x , y\bigg) \frac{1}{\sqrt{t (-\phi^{\prime\prime}(w))}} \exp\Big(-t \big(\phi(w) - w\phi'(w)\big) \Big) {\: \rm d} u \end{align} $$
$$ \begin{align} I_1 \approx \frac{1}{\phi^{-1}(1/t)} \int_0^{1} h\bigg(\frac{u}{\phi^{-1}(1/t)}, x , y\bigg) \frac{1}{\sqrt{t (-\phi^{\prime\prime}(w))}} \exp\Big(-t \big(\phi(w) - w\phi'(w)\big) \Big) {\: \rm d} u \end{align} $$
where
 $$ \begin{align*} w = (\phi')^{-1}\bigg(\frac{u}{t \phi^{-1}(1/t)} \bigg). \end{align*} $$
$$ \begin{align*} w = (\phi')^{-1}\bigg(\frac{u}{t \phi^{-1}(1/t)} \bigg). \end{align*} $$
Recall that, by Proposition 2.3, for all
![]() $r> x_0$
we have
$r> x_0$
we have
We can assume that
 $$ \begin{align*} t \phi\left(2 (CC_1)^{\frac{1}{1-\beta}} x_0 \right) < 1. \end{align*} $$
$$ \begin{align*} t \phi\left(2 (CC_1)^{\frac{1}{1-\beta}} x_0 \right) < 1. \end{align*} $$
By (5.6) and the weak upper scaling of
![]() $\phi '$
, we get
$\phi '$
, we get
 $$ \begin{align*} \phi'\Big(\phi^{-1}(1/t)\Big) \leq \frac{1}{t \phi^{-1}(1/t)} &\leq C_1 \phi'\big(\phi^{-1}(1/t)\big)\\ &\leq \phi'\Big((CC_1)^{-\frac{1}{1-\beta}} \phi^{-1}(1/t)\Big); \end{align*} $$
$$ \begin{align*} \phi'\Big(\phi^{-1}(1/t)\Big) \leq \frac{1}{t \phi^{-1}(1/t)} &\leq C_1 \phi'\big(\phi^{-1}(1/t)\big)\\ &\leq \phi'\Big((CC_1)^{-\frac{1}{1-\beta}} \phi^{-1}(1/t)\Big); \end{align*} $$
thus,
 $$ \begin{align*} (\phi')^{-1}\bigg(\frac{1}{t \phi^{-1}(1/t)} \bigg) \approx \phi^{-1}(1/t). \end{align*} $$
$$ \begin{align*} (\phi')^{-1}\bigg(\frac{1}{t \phi^{-1}(1/t)} \bigg) \approx \phi^{-1}(1/t). \end{align*} $$
Hence, by (5.3) and (5.4), we obtain
 $$ \begin{align} u^{-\frac{1}{1-\alpha}} \phi^{-1}(1/t) \lesssim w \lesssim u^{-\frac{1}{1-\beta}} \phi^{-1}(1/t), \quad u \in (0, 1]. \end{align} $$
$$ \begin{align} u^{-\frac{1}{1-\alpha}} \phi^{-1}(1/t) \lesssim w \lesssim u^{-\frac{1}{1-\beta}} \phi^{-1}(1/t), \quad u \in (0, 1]. \end{align} $$
Moreover, since
![]() $w> x_0$
, by (5.6) and Proposition 4.6,
$w> x_0$
, by (5.6) and Proposition 4.6,
 $$ \begin{align*} w \phi'(w) \gtrsim \phi(w) - w \phi'(w) &= \int_0^{w} \varphi(u) \frac{{\textrm{d}} u}{u} \\ &\geq \int_{x_0}^{w} \varphi(u) \frac{{\textrm{d}} u}{u} \gtrsim w \phi'(w). \end{align*} $$
$$ \begin{align*} w \phi'(w) \gtrsim \phi(w) - w \phi'(w) &= \int_0^{w} \varphi(u) \frac{{\textrm{d}} u}{u} \\ &\geq \int_{x_0}^{w} \varphi(u) \frac{{\textrm{d}} u}{u} \gtrsim w \phi'(w). \end{align*} $$
Thus, (5.7) entails that
 $$ \begin{align} u^{-\frac{\alpha}{1-\alpha}} \lesssim t \big(\phi(w) - w \phi'(w)\big) \lesssim u^{-\frac{\beta}{1-\beta}}, \quad u \in (0, 1]. \end{align} $$
$$ \begin{align} u^{-\frac{\alpha}{1-\alpha}} \lesssim t \big(\phi(w) - w \phi'(w)\big) \lesssim u^{-\frac{\beta}{1-\beta}}, \quad u \in (0, 1]. \end{align} $$
Next, by Proposition 4.6 and (5.6), we get
 $$ \begin{align*} \frac{1}{\sqrt{t (-\phi^{\prime\prime}(w))}} \approx \frac{w}{\sqrt{t \phi(w)}} \approx \sqrt{u^{-1} \phi^{-1}(1/t) w}. \end{align*} $$
$$ \begin{align*} \frac{1}{\sqrt{t (-\phi^{\prime\prime}(w))}} \approx \frac{w}{\sqrt{t \phi(w)}} \approx \sqrt{u^{-1} \phi^{-1}(1/t) w}. \end{align*} $$
Therefore, by (5.7),
 $$ \begin{align} u^{-\frac{2-\alpha}{2(1-\alpha)}} \phi^{-1}(1/t) \lesssim \frac{1}{\sqrt{t (-\phi^{\prime\prime}(w))}} \lesssim u^{-\frac{2-\beta}{2(1-\beta)}} \phi^{-1}(1/t), \quad u \in (0, 1]. \end{align} $$
$$ \begin{align} u^{-\frac{2-\alpha}{2(1-\alpha)}} \phi^{-1}(1/t) \lesssim \frac{1}{\sqrt{t (-\phi^{\prime\prime}(w))}} \lesssim u^{-\frac{2-\beta}{2(1-\beta)}} \phi^{-1}(1/t), \quad u \in (0, 1]. \end{align} $$
Now, by (5.5) and (5.1) together with (5.8) and (5.9), we can estimate
 $$ \begin{align} I_1 &\lesssim \big(\phi^{-1}(1/t) \big)^{\frac{n}{\gamma}} \int_0^{1} \Phi_2\left(u^{-\frac{1}{\gamma}} A^{\frac{1}{\gamma}}\right) u^{-\frac{n}{\gamma} - \frac{2-\beta}{2(1-\beta)}} \exp\Big(-C^{\prime\prime} u^{-\frac{\alpha}{1-\alpha}} \Big) {\: \rm d} u \end{align} $$
$$ \begin{align} I_1 &\lesssim \big(\phi^{-1}(1/t) \big)^{\frac{n}{\gamma}} \int_0^{1} \Phi_2\left(u^{-\frac{1}{\gamma}} A^{\frac{1}{\gamma}}\right) u^{-\frac{n}{\gamma} - \frac{2-\beta}{2(1-\beta)}} \exp\Big(-C^{\prime\prime} u^{-\frac{\alpha}{1-\alpha}} \Big) {\: \rm d} u \end{align} $$
and
 $$ \begin{align} I_1 &\gtrsim \big(\phi^{-1}(1/t) \big)^{\frac{n}{\gamma}} \int_0^{1} \Phi_1\left(u^{-\frac{1}{\gamma}} A^{\frac{1}{\gamma}}\right) u^{-\frac{n}{\gamma} - \frac{2-\alpha}{2(1-\alpha)}} \exp\Big(-C' u^{-\frac{\beta}{1-\beta}} \Big) {\: \rm d} u, \end{align} $$
$$ \begin{align} I_1 &\gtrsim \big(\phi^{-1}(1/t) \big)^{\frac{n}{\gamma}} \int_0^{1} \Phi_1\left(u^{-\frac{1}{\gamma}} A^{\frac{1}{\gamma}}\right) u^{-\frac{n}{\gamma} - \frac{2-\alpha}{2(1-\alpha)}} \exp\Big(-C' u^{-\frac{\beta}{1-\beta}} \Big) {\: \rm d} u, \end{align} $$
where
Suppose that
![]() $A \leq 1$
. Since
$A \leq 1$
. Since
![]() $\Phi _1$
and
$\Phi _1$
and
![]() $\Phi _2$
are nonincreasing, by (5.10) and (5.11), we easily see that
$\Phi _2$
are nonincreasing, by (5.10) and (5.11), we easily see that
 $$ \begin{align*} I_1 \approx \big(\phi^{-1}(1/t) \big)^{\frac{n}{\gamma}}. \end{align*} $$
$$ \begin{align*} I_1 \approx \big(\phi^{-1}(1/t) \big)^{\frac{n}{\gamma}}. \end{align*} $$
We also have
 $$ \begin{align*} I_2 \lesssim \int_{\frac{1}{\phi^{-1}(1/t)}}^{\infty} s^{-\frac{n}{\gamma}} p(t, s) {\: \rm d} s \lesssim \big(\phi^{-1}(1/t) \big)^{\frac{n}{\gamma}}. \end{align*} $$
$$ \begin{align*} I_2 \lesssim \int_{\frac{1}{\phi^{-1}(1/t)}}^{\infty} s^{-\frac{n}{\gamma}} p(t, s) {\: \rm d} s \lesssim \big(\phi^{-1}(1/t) \big)^{\frac{n}{\gamma}}. \end{align*} $$
Therefore,
 $$ \begin{align*} H(t, x, y) \approx \big(\phi^{-1}(1/t) \big)^{\frac{n}{\gamma}}. \end{align*} $$
$$ \begin{align*} H(t, x, y) \approx \big(\phi^{-1}(1/t) \big)^{\frac{n}{\gamma}}. \end{align*} $$
We now turn to the case
![]() $A> 1$
. By (5.2) and (5.10),
$A> 1$
. By (5.2) and (5.10),
 $$ \begin{align} \nonumber I_1 &\lesssim \big(\phi^{-1}(1/t) \big)^{\frac{n}{\gamma}} A^{-\frac{n}{\gamma}-1} \int_0^{1} u^{-\frac{\beta}{2(1-\beta)}} \exp\Big(-C^{\prime\prime} u^{-\frac{\alpha}{1-\alpha}} \Big) {\: \rm d} u \\ &\lesssim A^{-1} \tau(x, y)^{-n}. \end{align} $$
$$ \begin{align} \nonumber I_1 &\lesssim \big(\phi^{-1}(1/t) \big)^{\frac{n}{\gamma}} A^{-\frac{n}{\gamma}-1} \int_0^{1} u^{-\frac{\beta}{2(1-\beta)}} \exp\Big(-C^{\prime\prime} u^{-\frac{\alpha}{1-\alpha}} \Big) {\: \rm d} u \\ &\lesssim A^{-1} \tau(x, y)^{-n}. \end{align} $$
It remains to estimate
![]() $I_2$
. Let us observe that for all
$I_2$
. Let us observe that for all
![]() $r> x_0$
, if
$r> x_0$
, if
![]() $u \geq 1$
, then by the weak upper scaling of
$u \geq 1$
, then by the weak upper scaling of
![]() $\phi $
, we have
$\phi $
, we have
On the other hand, if
![]() $0 < u \leq 1$
, then by (2.10) and the monotonicity of
$0 < u \leq 1$
, then by (2.10) and the monotonicity of
![]() $\phi $
, we get
$\phi $
, we get
Therefore, for all
![]() $u> 0$
and
$u> 0$
and
![]() $r> x_0$
,
$r> x_0$
,
Since
![]() $\tau (x, y)^{-\gamma }> x_0$
, by Theorem 4.17, (5.1) and estimates (5.13), we get
$\tau (x, y)^{-\gamma }> x_0$
, by Theorem 4.17, (5.1) and estimates (5.13), we get
 $$ \begin{align*} I_2 &\lesssim t \phi\big(\tau(x, y)^{-\gamma}\big) \tau(x, y)^{-n} \int_{1/A}^\infty \Phi_2\left(u^{-\frac{1}{\gamma}} \right) u^{-\frac{n}{\gamma}-1} \max{\left\{1, u^{-\beta} \right\}} {\: \rm d} u \end{align*} $$
$$ \begin{align*} I_2 &\lesssim t \phi\big(\tau(x, y)^{-\gamma}\big) \tau(x, y)^{-n} \int_{1/A}^\infty \Phi_2\left(u^{-\frac{1}{\gamma}} \right) u^{-\frac{n}{\gamma}-1} \max{\left\{1, u^{-\beta} \right\}} {\: \rm d} u \end{align*} $$
and
 $$ \begin{align*} I_2 &\gtrsim t \phi\big(\tau(x, y)^{-\gamma}\big) \tau(x, y)^{-n} \int_{1/A}^\infty \Phi_1\left(u^{-\frac{1}{\gamma}}\right) u^{-\frac{n}{\gamma} - 1} \min{\{1, u\} } {\: \rm d} u. \end{align*} $$
$$ \begin{align*} I_2 &\gtrsim t \phi\big(\tau(x, y)^{-\gamma}\big) \tau(x, y)^{-n} \int_{1/A}^\infty \Phi_1\left(u^{-\frac{1}{\gamma}}\right) u^{-\frac{n}{\gamma} - 1} \min{\{1, u\} } {\: \rm d} u. \end{align*} $$
By (5.2), we have
 $$ \begin{align*} \int_0^1 \Phi_2\left(u^{-\frac{1}{\gamma}} \right) u^{-\frac{n}{\gamma}-\beta-1} {\: \rm d} u \lesssim \int_0^1 u^{-\beta} {\: \rm d} u < \infty; \end{align*} $$
$$ \begin{align*} \int_0^1 \Phi_2\left(u^{-\frac{1}{\gamma}} \right) u^{-\frac{n}{\gamma}-\beta-1} {\: \rm d} u \lesssim \int_0^1 u^{-\beta} {\: \rm d} u < \infty; \end{align*} $$
thus,
 $$ \begin{align*} I_2 \approx t \phi\big(\tau(x, y)^{-\gamma}\big) \tau(x, y)^{-n}. \end{align*} $$
$$ \begin{align*} I_2 \approx t \phi\big(\tau(x, y)^{-\gamma}\big) \tau(x, y)^{-n}. \end{align*} $$
Finally, since
![]() $A> 1$
, by (2.10), we have
$A> 1$
, by (2.10), we have
 $$ \begin{align*} t \phi\big(\tau(x, y)^{-\gamma}\big) = t \phi\big(A^{-1} \phi^{-1}(1/t)\big) \geq A^{-1}; \end{align*} $$
$$ \begin{align*} t \phi\big(\tau(x, y)^{-\gamma}\big) = t \phi\big(A^{-1} \phi^{-1}(1/t)\big) \geq A^{-1}; \end{align*} $$
hence, by (5.12),
 $$ \begin{align*} I_1 \lesssim t \phi\big(\tau(x, y)^{-\gamma}\big) \tau(x, y)^{-n}, \end{align*} $$
$$ \begin{align*} I_1 \lesssim t \phi\big(\tau(x, y)^{-\gamma}\big) \tau(x, y)^{-n}, \end{align*} $$
proving the claim.
Example 5.2. Let
![]() $(\mathscr {X}, \tau )$
be a nested fractal with the geodesic metric on
$(\mathscr {X}, \tau )$
be a nested fractal with the geodesic metric on
![]() $\mathscr {X}$
. Let
$\mathscr {X}$
. Let
![]() $d_w$
and
$d_w$
and
![]() $d_f$
be the walk dimension and the Hausdorff dimension of
$d_f$
be the walk dimension and the Hausdorff dimension of
![]() $\mathscr {X}$
, respectively. Let
$\mathscr {X}$
, respectively. Let
![]() $(X_t \colon t \geq 0)$
be the diffusion on
$(X_t \colon t \geq 0)$
be the diffusion on
![]() $\mathscr {X}$
constructed in [Reference Barlow2, Section 7]. By [Reference Barlow2, Theorem 8.18], the corresponding heat kernel satisfies (5.1) with
$\mathscr {X}$
constructed in [Reference Barlow2, Section 7]. By [Reference Barlow2, Theorem 8.18], the corresponding heat kernel satisfies (5.1) with
![]() $n = d_f$
,
$n = d_f$
,
![]() $\gamma = d_w$
, and
$\gamma = d_w$
, and
 $$ \begin{align*} \Phi_1(s) = \Phi_2(s) = \exp\left(-s^{\frac{\gamma}{\gamma-1}} \right). \end{align*} $$
$$ \begin{align*} \Phi_1(s) = \Phi_2(s) = \exp\left(-s^{\frac{\gamma}{\gamma-1}} \right). \end{align*} $$
Let
![]() $\mathbf {T}$
be a subordinator with the Laplace exponent
$\mathbf {T}$
be a subordinator with the Laplace exponent
where
![]() $\alpha \in (0, 1)$
and
$\alpha \in (0, 1)$
and
![]() $\sigma \in \mathbb {R}$
. Then, by Claim 5.1, the process
$\sigma \in \mathbb {R}$
. Then, by Claim 5.1, the process
![]() $(X_{T_t} \colon t \geq 0)$
has density
$(X_{T_t} \colon t \geq 0)$
has density
![]() $H(t, x, y)$
such that for all
$H(t, x, y)$
such that for all
![]() $x, y \in \mathscr {X}$
and
$x, y \in \mathscr {X}$
and
![]() $t> 0$
,
$t> 0$
,
-
•. if
 $t> \tau (x, y)^{\alpha \gamma } \log ^{-\sigma }\left (2 + \tau (x, y)^{-\gamma }\right )$
, then
$t> \tau (x, y)^{\alpha \gamma } \log ^{-\sigma }\left (2 + \tau (x, y)^{-\gamma }\right )$
, then  $$ \begin{align*} H(t, x, y) \approx t^{-\frac{n}{\alpha\gamma}} \log^{-\frac{\sigma n}{\alpha\gamma}}\big(2+t^{-1}\big), \end{align*} $$
$$ \begin{align*} H(t, x, y) \approx t^{-\frac{n}{\alpha\gamma}} \log^{-\frac{\sigma n}{\alpha\gamma}}\big(2+t^{-1}\big), \end{align*} $$
-
•. if
 $t < \tau (x, y)^{\alpha \gamma } \log ^{-\sigma }\left (2 + \tau (x, y)^{-\gamma }\right )$
, then
$t < \tau (x, y)^{\alpha \gamma } \log ^{-\sigma }\left (2 + \tau (x, y)^{-\gamma }\right )$
, then  $$ \begin{align*} H(t, x, y) \approx t \tau(x, y)^{-\alpha \gamma - n} \log^{\sigma}\big(2 + \tau(x, y)^{-\gamma}\big). \end{align*} $$
$$ \begin{align*} H(t, x, y) \approx t \tau(x, y)^{-\alpha \gamma - n} \log^{\sigma}\big(2 + \tau(x, y)^{-\gamma}\big). \end{align*} $$
Example 5.3. Let
![]() $(\mathscr {X}, \tau )$
be a complete manifold without boundary, having nonnegative Ricci curvature. Then by [Reference Li and Yau37], the heat kernel corresponding to the Laplace–Beltrami operator on
$(\mathscr {X}, \tau )$
be a complete manifold without boundary, having nonnegative Ricci curvature. Then by [Reference Li and Yau37], the heat kernel corresponding to the Laplace–Beltrami operator on
![]() $\mathscr {X}$
satisfies estimates (5.1) with
$\mathscr {X}$
satisfies estimates (5.1) with
 $$ \begin{align*} \Phi_1(s) = e^{-C_1 s^2}, \qquad \Phi_2(s) = e^{-C_2 s^2}. \end{align*} $$
$$ \begin{align*} \Phi_1(s) = e^{-C_1 s^2}, \qquad \Phi_2(s) = e^{-C_2 s^2}. \end{align*} $$
Now, one can take
![]() $\mathbf {T}$
with a Lévy–Khintchine exponent regularly varying at infinity with index
$\mathbf {T}$
with a Lévy–Khintchine exponent regularly varying at infinity with index
![]() $\alpha \in (0,1)$
and apply Claim 5.1 to obtain the asymptotic behaviour of the subordinate process.
$\alpha \in (0,1)$
and apply Claim 5.1 to obtain the asymptotic behaviour of the subordinate process.
5.2. Green function estimates
Let
![]() $\mathbf {T} = (T_t \colon t \geq 0)$
be a subordinator with the Laplace exponent
$\mathbf {T} = (T_t \colon t \geq 0)$
be a subordinator with the Laplace exponent
![]() $\phi $
. If
$\phi $
. If
![]() $-\phi ^{\prime \prime }$
has the weak lower scaling property of index
$-\phi ^{\prime \prime }$
has the weak lower scaling property of index
![]() $\alpha -2$
for some
$\alpha -2$
for some
![]() $\alpha> 0$
, then the probability distribution of
$\alpha> 0$
, then the probability distribution of
![]() $T_t$
has a density
$T_t$
has a density
![]() $p(t, \: \cdot \:)$
; see Theorem 3.3. In this section we want to derive sharp estimates on the Green function based on Sections 3 and 4. Let us recall that the Green function is
$p(t, \: \cdot \:)$
; see Theorem 3.3. In this section we want to derive sharp estimates on the Green function based on Sections 3 and 4. Let us recall that the Green function is
 $$ \begin{align*} G(x) = \int_0^{\infty} p(t,x) {\: \rm d} t, \qquad x>0. \end{align*} $$
$$ \begin{align*} G(x) = \int_0^{\infty} p(t,x) {\: \rm d} t, \qquad x>0. \end{align*} $$
We set
 $$ \begin{align*} f(x) = \frac{\varphi(x)}{\phi'(x)}, \qquad x>0. \end{align*} $$
$$ \begin{align*} f(x) = \frac{\varphi(x)}{\phi'(x)}, \qquad x>0. \end{align*} $$
Let us denote by
![]() $f^{-1}$
the generalised inverse of f; that is,
$f^{-1}$
the generalised inverse of f; that is,
where
 $$ \begin{align*} f^*(r) = \mathop{\mathrm{sup}}\limits_{0<x\leq r}f(x). \end{align*} $$
$$ \begin{align*} f^*(r) = \mathop{\mathrm{sup}}\limits_{0<x\leq r}f(x). \end{align*} $$
Notice that by (2.9) and Proposition 2.3, for all
![]() $x> x_0$
,
$x> x_0$
,
In view of (4.2) and Proposition 4.3, the function
![]() $\varphi $
is almost increasing; thus, by monotonicity of
$\varphi $
is almost increasing; thus, by monotonicity of
![]() $\phi '$
, f is almost increasing as well. Therefore, there is
$\phi '$
, f is almost increasing as well. Therefore, there is
![]() $c_0 \in (0, 1]$
such that for all
$c_0 \in (0, 1]$
such that for all
![]() $x> x_0$
,
$x> x_0$
,
Moreover, f has the doubling property on
![]() $(x_0,\infty )$
. Since
$(x_0,\infty )$
. Since
![]() $\varphi $
belongs to
$\varphi $
belongs to
![]() $\mathrm {WLSC}(\alpha ,c,x_0)$
, by monotonicity of
$\mathrm {WLSC}(\alpha ,c,x_0)$
, by monotonicity of
![]() $\phi '$
, we conclude that f belongs to
$\phi '$
, we conclude that f belongs to
![]() $\mathrm {WLSC}(\alpha ,c,x_0)$
. It follows that
$\mathrm {WLSC}(\alpha ,c,x_0)$
. It follows that
![]() $f^{-1} \in \mathrm {WUSC}(1/\alpha ,C,f^*(x_0))$
for some
$f^{-1} \in \mathrm {WUSC}(1/\alpha ,C,f^*(x_0))$
for some
![]() $C \geq 1$
and since
$C \geq 1$
and since
![]() $f^{-1}$
is increasing, we infer that
$f^{-1}$
is increasing, we infer that
![]() $f^{-1}$
also has doubling property on
$f^{-1}$
also has doubling property on
![]() $(f^*(x_0),\infty )$
.
$(f^*(x_0),\infty )$
.
Proposition 5.4. Suppose that
![]() $b=0$
and
$b=0$
and
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0,1]$
,
$c \in (0,1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
. Then for each
$\alpha>0$
. Then for each
![]() $A>0$
and
$A>0$
and
![]() $M>0$
there is
$M>0$
there is
![]() $C \geq 1$
so that for all
$C \geq 1$
so that for all
![]() $x < A/x_0$
,
$x < A/x_0$
,
 $$ \begin{align*} C^{-1} \frac{1}{x\phi( 1/x)} \leq \int_{\frac{x}{\phi'( f^{-1}(M/x))}}^{\infty} p(t,x) {\: \rm d} t \leq C\frac{1}{x\phi( 1/x)}. \end{align*} $$
$$ \begin{align*} C^{-1} \frac{1}{x\phi( 1/x)} \leq \int_{\frac{x}{\phi'( f^{-1}(M/x))}}^{\infty} p(t,x) {\: \rm d} t \leq C\frac{1}{x\phi( 1/x)}. \end{align*} $$
In particular, for each
![]() $A>0$
there is
$A>0$
there is
![]() $C> 0$
such that for all
$C> 0$
such that for all
![]() $x < A/x_0$
,
$x < A/x_0$
,
 $$ \begin{align*} G(x) \geq C \frac{1}{x\phi ( 1/x)}. \end{align*} $$
$$ \begin{align*} G(x) \geq C \frac{1}{x\phi ( 1/x)}. \end{align*} $$
Proof. For
![]() $M> 0$
and
$M> 0$
and
![]() $x> 0$
we set
$x> 0$
we set
 $$ \begin{align*} I_M(x)=\int_{\frac{x}{\phi'(f^{-1}(M/x))}}^{\infty} p(t,x) {\: \rm d} t. \end{align*} $$
$$ \begin{align*} I_M(x)=\int_{\frac{x}{\phi'(f^{-1}(M/x))}}^{\infty} p(t,x) {\: \rm d} t. \end{align*} $$
Let us first show that for each
![]() $M>0$
there are
$M>0$
there are
![]() $A_M>0$
and
$A_M>0$
and
![]() $C \geq 1$
such that for all
$C \geq 1$
such that for all
![]() $x<A_M/x_0$
,
$x<A_M/x_0$
,
 $$ \begin{align} C^{-1} \frac{1}{x\phi( 1/x)} \leq \int_{\frac{x}{\phi'( f^{-1}(M/x))}}^{\infty} p(t,x) {\: \rm d} t \leq C\frac{1}{x\phi( 1/x)}. \end{align} $$
$$ \begin{align} C^{-1} \frac{1}{x\phi( 1/x)} \leq \int_{\frac{x}{\phi'( f^{-1}(M/x))}}^{\infty} p(t,x) {\: \rm d} t \leq C\frac{1}{x\phi( 1/x)}. \end{align} $$
Let
 $$ \begin{align*} A_M = \min \big\{ M, c_0^{-1} M_0 \big\} \cdot \min\bigg\{1, \frac{x_0}{f^*(x_0)}\bigg\} \end{align*} $$
$$ \begin{align*} A_M = \min \big\{ M, c_0^{-1} M_0 \big\} \cdot \min\bigg\{1, \frac{x_0}{f^*(x_0)}\bigg\} \end{align*} $$
where
![]() $M_0$
is determined in Corollary 3.5, and
$M_0$
is determined in Corollary 3.5, and
![]() $c_0$
is taken from (5.15). We claim that the following holds true.
$c_0$
is taken from (5.15). We claim that the following holds true.
Claim 5.5. For each
![]() $M>0$
there is
$M>0$
there is
![]() $C \geq 1$
so that for all
$C \geq 1$
so that for all
![]() $x < A_M/x_0$
,
$x < A_M/x_0$
,
 $$ \begin{align} C^{-1} \frac{1}{\phi'\big(f^{-1}(1/x)\big)} \leq I_M(x) \leq C \frac{1}{\phi'\big(f^{-1}(1/x)\big)}. \end{align} $$
$$ \begin{align} C^{-1} \frac{1}{\phi'\big(f^{-1}(1/x)\big)} \leq I_M(x) \leq C \frac{1}{\phi'\big(f^{-1}(1/x)\big)}. \end{align} $$
Suppose that
 $$ \begin{align} t> \frac{x}{\phi'\big(f^{-1}(M_1/x)\big)} \end{align} $$
$$ \begin{align} t> \frac{x}{\phi'\big(f^{-1}(M_1/x)\big)} \end{align} $$
with
 $M_1 = c_0^{-1} M_0$
. Notice that for
$M_1 = c_0^{-1} M_0$
. Notice that for
![]() $x < A_M/x_0$
, we have
$x < A_M/x_0$
, we have
![]() $x < M_1/f^*(x_0)$
. Hence,
$x < M_1/f^*(x_0)$
. Hence,
 $x_0 \leq f^{-1}\big (M_1 /x\big )$
; thus, by monotonicity of
$x_0 \leq f^{-1}\big (M_1 /x\big )$
; thus, by monotonicity of
![]() $\phi '$
, we obtain
$\phi '$
, we obtain
 $$ \begin{align} \nonumber \frac{x}{t} &\leq \phi'\big(f^{-1}(M_1/x)\big) \\ &\leq \phi'(x_0). \end{align} $$
$$ \begin{align} \nonumber \frac{x}{t} &\leq \phi'\big(f^{-1}(M_1/x)\big) \\ &\leq \phi'(x_0). \end{align} $$
Moreover, for
![]() $w = (\phi ')^{-1}(x/t)$
, the condition (5.18) implies that
$w = (\phi ')^{-1}(x/t)$
, the condition (5.18) implies that
which together with (5.15) gives
 $$ \begin{align} \nonumber t \varphi(w) = x f(w) &\geq c_0 x f^*(w) \\ &\geq M_0. \end{align} $$
$$ \begin{align} \nonumber t \varphi(w) = x f(w) &\geq c_0 x f^*(w) \\ &\geq M_0. \end{align} $$
Now, to justify the claim, let us first consider
![]() $M \geq M_1$
. In view of (5.19) and (5.20), we can apply Corollary 3.5 to get
$M \geq M_1$
. In view of (5.19) and (5.20), we can apply Corollary 3.5 to get
 $$ \begin{align*} I_M(x) \approx \int_{\frac{x}{\phi'( f^{-1}(M/x))}}^{\infty} \frac{1}{\sqrt{t (-\phi^{\prime\prime} (w))}} \exp\Big\{-t \big(\phi(w) - w \phi'(w)\big)\Big\} {\: \rm d} t. \end{align*} $$
$$ \begin{align*} I_M(x) \approx \int_{\frac{x}{\phi'( f^{-1}(M/x))}}^{\infty} \frac{1}{\sqrt{t (-\phi^{\prime\prime} (w))}} \exp\Big\{-t \big(\phi(w) - w \phi'(w)\big)\Big\} {\: \rm d} t. \end{align*} $$
Since by Proposition 4.1 and Remark 3.2, for all
![]() $w>x_0$
,
$w>x_0$
,
 $$ \begin{align*} \phi(w)-w\phi'(w) &\approx h(1/w) \\ &\approx K(1/w) \\ & \approx w^2 \big( -\phi^{\prime\prime}(w) \big), \end{align*} $$
$$ \begin{align*} \phi(w)-w\phi'(w) &\approx h(1/w) \\ &\approx K(1/w) \\ & \approx w^2 \big( -\phi^{\prime\prime}(w) \big), \end{align*} $$
after the change of variables
![]() $t = x / \phi '(s)$
, we can find
$t = x / \phi '(s)$
, we can find
![]() $C_2 \geq 1$
such that for all
$C_2 \geq 1$
such that for all
![]() $x < A_M/x_0$
,
$x < A_M/x_0$
,
 $$ \begin{align} \begin{aligned} \int_{f^{-1}(M/x)}^{\infty} \exp\{ -C_2 x f(s) \} \sqrt{xf(s)} \frac{{\textrm{d}}s}{s\phi'(s)} &\lesssim I_M(x) \\ &\lesssim \int_{f^{-1}(M/x)}^{\infty} \exp\{ -C_2^{-1} xf(s) \} \sqrt{xf(s)} \frac{{\textrm{d}}s}{s\phi'(s)}.\end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \int_{f^{-1}(M/x)}^{\infty} \exp\{ -C_2 x f(s) \} \sqrt{xf(s)} \frac{{\textrm{d}}s}{s\phi'(s)} &\lesssim I_M(x) \\ &\lesssim \int_{f^{-1}(M/x)}^{\infty} \exp\{ -C_2^{-1} xf(s) \} \sqrt{xf(s)} \frac{{\textrm{d}}s}{s\phi'(s)}.\end{aligned} \end{align} $$
Recall that
![]() $f^{-1}$
has the doubling property on
$f^{-1}$
has the doubling property on
![]() $(f^*(x_0),\infty )$
. Using now Proposition 2.3 and (5.15), we get
$(f^*(x_0),\infty )$
. Using now Proposition 2.3 and (5.15), we get
 $$ \begin{align} \nonumber I_M(x) &\gtrsim \int_{f^{-1}(M/x)}^{2f^{-1}(M/x)} \exp\{-C_2xf^*(s)\}\sqrt{xf^*(s)} \frac{{\textrm{d}}s}{\phi(s)} \\ \nonumber &\gtrsim \frac{1}{\phi \big( f^{-1}(M/x) \big) } f^{-1}(M/x) \\ &\gtrsim \frac{1}{\phi' \big( f^{-1}(M/x) \big)}, \end{align} $$
$$ \begin{align} \nonumber I_M(x) &\gtrsim \int_{f^{-1}(M/x)}^{2f^{-1}(M/x)} \exp\{-C_2xf^*(s)\}\sqrt{xf^*(s)} \frac{{\textrm{d}}s}{\phi(s)} \\ \nonumber &\gtrsim \frac{1}{\phi \big( f^{-1}(M/x) \big) } f^{-1}(M/x) \\ &\gtrsim \frac{1}{\phi' \big( f^{-1}(M/x) \big)}, \end{align} $$
where the implicit constants may depend on M. Therefore, by monotonicity of
![]() $f^{-1}$
and
$f^{-1}$
and
![]() $\phi '$
, the estimate (5.22) gives
$\phi '$
, the estimate (5.22) gives
 $$ \begin{align} I_M(x) \gtrsim \frac{1}{\phi' \big( f^{-1}(1/x) \big)}. \end{align} $$
$$ \begin{align} I_M(x) \gtrsim \frac{1}{\phi' \big( f^{-1}(1/x) \big)}. \end{align} $$
This proves the first inequality in (5.17).
We next observe that (5.14) entails that
![]() $f^{-1}(s) \gtrsim s$
for
$f^{-1}(s) \gtrsim s$
for
![]() $s> f^*(x_0)$
; thus, by (5.23),
$s> f^*(x_0)$
; thus, by (5.23),
 $$ \begin{align} \nonumber G(x) \geq I_{M_1}(x) &\gtrsim \frac{1}{\phi' (1/x)} \\ &\gtrsim \frac{1}{x \phi(1/x)} \end{align} $$
$$ \begin{align} \nonumber G(x) \geq I_{M_1}(x) &\gtrsim \frac{1}{\phi' (1/x)} \\ &\gtrsim \frac{1}{x \phi(1/x)} \end{align} $$
where the last estimate follows by Proposition 2.3.
We next show the second inequality in (5.17). By (5.21), Proposition 2.3 and monotonicity of
![]() $\phi $
,
$\phi $
,
 $$ \begin{align*} I_M(x) &\lesssim \int_{f^{-1}(M/x)}^{\infty} \exp\big\{ -C_2^{-1} xf(s) \big\} \sqrt{xf(s)} \frac{{\textrm{d}}s}{\phi(s)} \\ &\leq \frac{1}{\phi \big( f^{-1}(M/x) \big)} \int_{f^{-1}(M/x)}^{\infty} \exp\big\{ -C_2^{-1} xf(s) \big\} \sqrt{xf(s)} {\: \rm d} s \\ &\leq \frac{1}{\phi \big( f^{-1}(M/x) \big)} \int_{f^{-1}(M/x)}^{\infty} \exp \Big\{ -\tfrac{1}{2 C_2} xf(s) \Big\} {\: \rm d} s \end{align*} $$
$$ \begin{align*} I_M(x) &\lesssim \int_{f^{-1}(M/x)}^{\infty} \exp\big\{ -C_2^{-1} xf(s) \big\} \sqrt{xf(s)} \frac{{\textrm{d}}s}{\phi(s)} \\ &\leq \frac{1}{\phi \big( f^{-1}(M/x) \big)} \int_{f^{-1}(M/x)}^{\infty} \exp\big\{ -C_2^{-1} xf(s) \big\} \sqrt{xf(s)} {\: \rm d} s \\ &\leq \frac{1}{\phi \big( f^{-1}(M/x) \big)} \int_{f^{-1}(M/x)}^{\infty} \exp \Big\{ -\tfrac{1}{2 C_2} xf(s) \Big\} {\: \rm d} s \end{align*} $$
where in the last inequality we have used
 $$ \begin{align*} \exp \big\{ -C_2^{-1} xf(s) \big\} \sqrt{xf(s)} \leq \exp \Big\{ -\tfrac{1}{2 C_2} xf(s) \Big\}. \end{align*} $$
$$ \begin{align*} \exp \big\{ -C_2^{-1} xf(s) \big\} \sqrt{xf(s)} \leq \exp \Big\{ -\tfrac{1}{2 C_2} xf(s) \Big\}. \end{align*} $$
Since
![]() $\varphi \in \mathrm {WLSC}(\alpha ,c,x_0)$
, by [Reference Bogdan, Grzywny and Ryznar6, Lemma 16],
$\varphi \in \mathrm {WLSC}(\alpha ,c,x_0)$
, by [Reference Bogdan, Grzywny and Ryznar6, Lemma 16],
 $$ \begin{align*} \int_{\mathbb{R}} \exp\big\{ -C_2^{-1} xf({\lvert {s} \rvert}) \big\}{\: \rm d} s \lesssim f^{-1}\big(M_1/ x \big). \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}} \exp\big\{ -C_2^{-1} xf({\lvert {s} \rvert}) \big\}{\: \rm d} s \lesssim f^{-1}\big(M_1/ x \big). \end{align*} $$
Finally, the doubling property of
![]() $f^{-1}$
, monotonicity of
$f^{-1}$
, monotonicity of
![]() $\phi $
and Proposition 2.3 give
$\phi $
and Proposition 2.3 give
 $$ \begin{align*} I_M(x) &\lesssim \frac{1}{\phi \big( f^{-1}(M/x) \big)} f^{-1}\big(M_1/x\big) \\ &\lesssim \frac{1}{\phi' \big( f^{-1}(1/x) \big)} \end{align*} $$
$$ \begin{align*} I_M(x) &\lesssim \frac{1}{\phi \big( f^{-1}(M/x) \big)} f^{-1}\big(M_1/x\big) \\ &\lesssim \frac{1}{\phi' \big( f^{-1}(1/x) \big)} \end{align*} $$
where the implied constant may depend on M. This finishes the proof of (5.17) for
![]() $M \geq M_1$
.
$M \geq M_1$
.
We next consider
![]() $0 < M < M_1$
. By monotonicity, the lower estimate remains valid for all
$0 < M < M_1$
. By monotonicity, the lower estimate remains valid for all
![]() $M> 0$
. Therefore, it is enough to show that for each
$M> 0$
. Therefore, it is enough to show that for each
![]() $0 < M < M_1$
, there is
$0 < M < M_1$
, there is
![]() $C \geq 1$
such that for all
$C \geq 1$
such that for all
![]() $x < A_M/x_0$
,
$x < A_M/x_0$
,
 $$ \begin{align*} \int_{\frac{x}{\phi'( f^{-1}(M/x))}}^{\frac{x}{\phi'( f^{-1}(M_1/x))}} p(t,x) {\: \rm d} t \leq C \frac{1}{\phi' \big( f^{-1}(1/x) \big)}. \end{align*} $$
$$ \begin{align*} \int_{\frac{x}{\phi'( f^{-1}(M/x))}}^{\frac{x}{\phi'( f^{-1}(M_1/x))}} p(t,x) {\: \rm d} t \leq C \frac{1}{\phi' \big( f^{-1}(1/x) \big)}. \end{align*} $$
By [Reference Grzywny and Szczypkowski23, Theorem 3.1], there is
![]() $t_0> 0$
such that for all
$t_0> 0$
such that for all
![]() $0 < t < t_0$
,
$0 < t < t_0$
,
If
![]() $x_0=0$
, then
$x_0=0$
, then
![]() $t_0=\infty $
. Since
$t_0=\infty $
. Since
![]() $\varphi $
is almost increasing we have
$\varphi $
is almost increasing we have
 $$ \begin{align*} \frac{x}{\phi' \big( f^{-1}(M_1/x) \big)} &\leq \frac{M_1}{\varphi \big( f^{-1}(M_1 /x) \big)} \\ &\lesssim \frac{M_1}{\varphi \big( f^{-1}(M_1 x_0 /A) \big)}. \end{align*} $$
$$ \begin{align*} \frac{x}{\phi' \big( f^{-1}(M_1/x) \big)} &\leq \frac{M_1}{\varphi \big( f^{-1}(M_1 /x) \big)} \\ &\lesssim \frac{M_1}{\varphi \big( f^{-1}(M_1 x_0 /A) \big)}. \end{align*} $$
Hence, by continuity and positivity of
![]() $p(t,x)$
and
$p(t,x)$
and
![]() $\varphi ^{-1}(1/t)$
, we can take
$\varphi ^{-1}(1/t)$
, we can take
 $$ \begin{align*} t_0 \geq \frac{x}{\phi' \big( f^{-1}(M_1 / x ) \big)}. \end{align*} $$
$$ \begin{align*} t_0 \geq \frac{x}{\phi' \big( f^{-1}(M_1 / x ) \big)}. \end{align*} $$
Therefore, by the change of variables
![]() $t = x/\phi '(s)$
we get
$t = x/\phi '(s)$
we get
 $$ \begin{align*} \int_{\frac{x}{\phi'( f^{-1}(M/x))}}^{\frac{x}{\phi'( f^{-1}(M_1/x))}} p(t,x) {\: \rm d} t &\lesssim \int_{\frac{x}{\phi'( f^{-1}(M/x) )}}^{\frac{x}{\phi'( f^{-1}(M_1/x))}} \varphi^{-1}(1/t) {\: \rm d} t \\ &= x \int_{f^{-1}(M/x)}^{f^{-1}(M_1/x)} \varphi^{-1} \bigg( \frac{\phi'(s)}{x} \bigg) f(s) \frac{{\textrm{d}}s}{s^2 \phi'(s)}. \end{align*} $$
$$ \begin{align*} \int_{\frac{x}{\phi'( f^{-1}(M/x))}}^{\frac{x}{\phi'( f^{-1}(M_1/x))}} p(t,x) {\: \rm d} t &\lesssim \int_{\frac{x}{\phi'( f^{-1}(M/x) )}}^{\frac{x}{\phi'( f^{-1}(M_1/x))}} \varphi^{-1}(1/t) {\: \rm d} t \\ &= x \int_{f^{-1}(M/x)}^{f^{-1}(M_1/x)} \varphi^{-1} \bigg( \frac{\phi'(s)}{x} \bigg) f(s) \frac{{\textrm{d}}s}{s^2 \phi'(s)}. \end{align*} $$
Next, by monotonicity and the doubling property of
![]() $f^{-1}$
and
$f^{-1}$
and
![]() $\phi '$
, we obtain
$\phi '$
, we obtain
 $$ \begin{align} \nonumber \int_{\frac{x}{\phi'( f^{-1}(M/x))}}^{\frac{x}{\phi'( f^{-1}(M_1/x))}} p(t,x) {\: \rm d} t &\lesssim \frac{1}{\big(f^{-1}(M/x)\big)^2} \cdot \frac{1}{\phi' \big( f^{-1}(M_1/x) \big)} \int_{f^{-1}(M/x)}^{f^{-1}(M_1/x)} \varphi^{-1} \bigg( \frac{\phi'(s)}{x} \bigg) {\: \rm d} s \\ &\lesssim \frac{1}{\big(f^{-1}(1/x)\big)^2} \cdot \frac{1}{\phi' \big( f^{-1}(1/x) \big)} \int_{f^{-1}(M/x)}^{f^{-1}(M_1/x)} \varphi^{-1} \bigg( \frac{\phi'(s)}{x} \bigg) {\: \rm d} s. \end{align} $$
$$ \begin{align} \nonumber \int_{\frac{x}{\phi'( f^{-1}(M/x))}}^{\frac{x}{\phi'( f^{-1}(M_1/x))}} p(t,x) {\: \rm d} t &\lesssim \frac{1}{\big(f^{-1}(M/x)\big)^2} \cdot \frac{1}{\phi' \big( f^{-1}(M_1/x) \big)} \int_{f^{-1}(M/x)}^{f^{-1}(M_1/x)} \varphi^{-1} \bigg( \frac{\phi'(s)}{x} \bigg) {\: \rm d} s \\ &\lesssim \frac{1}{\big(f^{-1}(1/x)\big)^2} \cdot \frac{1}{\phi' \big( f^{-1}(1/x) \big)} \int_{f^{-1}(M/x)}^{f^{-1}(M_1/x)} \varphi^{-1} \bigg( \frac{\phi'(s)}{x} \bigg) {\: \rm d} s. \end{align} $$
Since by (5.15) for
![]() $s \geq f^{-1}(M/x)$
we have
$s \geq f^{-1}(M/x)$
we have
 $$ \begin{align*} \frac{\phi'(s)}{x} = \frac{\varphi(s)}{x f(s)} \lesssim \varphi^*(s), \end{align*} $$
$$ \begin{align*} \frac{\phi'(s)}{x} = \frac{\varphi(s)}{x f(s)} \lesssim \varphi^*(s), \end{align*} $$
by monotonicity of
![]() $\varphi ^{-1}$
, Proposition 4.3, Remark 4.4 and the doubling property of
$\varphi ^{-1}$
, Proposition 4.3, Remark 4.4 and the doubling property of
![]() $f^{-1}$
and
$f^{-1}$
and
![]() $\varphi ^{-1}$
, we get
$\varphi ^{-1}$
, we get
 $$ \begin{align*} \int_{f^{-1}(M/x)}^{f^{-1}(M_1/x)} \varphi^{-1} \bigg( \frac{\phi'(s)}{x} \bigg) {\: \rm d} s \lesssim \big(f^{-1}(1/x)\big)^2, \end{align*} $$
$$ \begin{align*} \int_{f^{-1}(M/x)}^{f^{-1}(M_1/x)} \varphi^{-1} \bigg( \frac{\phi'(s)}{x} \bigg) {\: \rm d} s \lesssim \big(f^{-1}(1/x)\big)^2, \end{align*} $$
which together with (5.25) gives (5.17) for
![]() $0 < M < M_1$
. This completes the proof of Claim 5.5.
$0 < M < M_1$
. This completes the proof of Claim 5.5.
Our next task is to deduce (5.16) from Claim 5.5. By Lemma 2.9 and Proposition 2.3, there is a complete Bernstein function
![]() $\tilde {\phi }$
such that
$\tilde {\phi }$
such that
![]() $\tilde {\phi } \approx \phi $
and
$\tilde {\phi } \approx \phi $
and
 $$ \begin{align*} f(x) \approx \tilde{f}(x) = \frac{x^2 \big(-\tilde{\phi}^{\prime\prime}(x) \big)}{\tilde{\phi}'(x)} \end{align*} $$
$$ \begin{align*} f(x) \approx \tilde{f}(x) = \frac{x^2 \big(-\tilde{\phi}^{\prime\prime}(x) \big)}{\tilde{\phi}'(x)} \end{align*} $$
for all
![]() $x> x_0$
. Let
$x> x_0$
. Let
![]() $\tilde {\mathbf {T}}$
be a subordinator with the Laplace exponent
$\tilde {\mathbf {T}}$
be a subordinator with the Laplace exponent
![]() $\tilde {\phi }$
. By
$\tilde {\phi }$
. By
![]() $\tilde {p}(t, \: \cdot \: )$
we denote the density of the probability distribution of
$\tilde {p}(t, \: \cdot \: )$
we denote the density of the probability distribution of
![]() $\tilde {T}_t$
. We set
$\tilde {T}_t$
. We set
 $$ \begin{align*} \tilde{G}(x) = \int_0^\infty \tilde{p}(t, x) {\: \rm d} t \end{align*} $$
$$ \begin{align*} \tilde{G}(x) = \int_0^\infty \tilde{p}(t, x) {\: \rm d} t \end{align*} $$
and
 $$ \begin{align*} \tilde{I}_M(x) = \int_{\frac{x}{\tilde{\phi}'(\tilde{f}^{-1}(M/x))}}^{\infty} \tilde{p}(t,x) {\: \rm d} t. \end{align*} $$
$$ \begin{align*} \tilde{I}_M(x) = \int_{\frac{x}{\tilde{\phi}'(\tilde{f}^{-1}(M/x))}}^{\infty} \tilde{p}(t,x) {\: \rm d} t. \end{align*} $$
Fix
![]() $M>0$
. By Claim 5.5, there is
$M>0$
. By Claim 5.5, there is
![]() $A_M> 0$
such that for all
$A_M> 0$
such that for all
![]() $x < A_M/x_0$
,
$x < A_M/x_0$
,
 $$ \begin{align} \begin{aligned} \tilde{I}_M(x) &\approx \frac{1}{\tilde{\phi}' \big( \tilde{f}^{-1}(1/x) \big)} \\ &\approx \frac{1}{\phi'\big(f^{-1}(1/x)\big)}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \tilde{I}_M(x) &\approx \frac{1}{\tilde{\phi}' \big( \tilde{f}^{-1}(1/x) \big)} \\ &\approx \frac{1}{\phi'\big(f^{-1}(1/x)\big)}. \end{aligned} \end{align} $$
On the other hand, since
![]() $\tilde {\phi }$
is the complete Bernstein function, by (5.24) and [Reference Kim, Song and Vondraček34, Corollary 2.6], there is
$\tilde {\phi }$
is the complete Bernstein function, by (5.24) and [Reference Kim, Song and Vondraček34, Corollary 2.6], there is
![]() $C_3 \geq 1$
such that
$C_3 \geq 1$
such that
 $$ \begin{align*} C_3^{-1} \frac{1}{x\tilde{\phi}(1/x)} \leq \tilde{I}_M(x) \leq \tilde{G}(x) \leq C_3 \frac{1}{x\tilde{\phi}(1/x)}. \end{align*} $$
$$ \begin{align*} C_3^{-1} \frac{1}{x\tilde{\phi}(1/x)} \leq \tilde{I}_M(x) \leq \tilde{G}(x) \leq C_3 \frac{1}{x\tilde{\phi}(1/x)}. \end{align*} $$
Therefore, by (5.26), for
![]() $x < A_M/x_0$
,
$x < A_M/x_0$
,
 $$ \begin{align} \begin{aligned} \frac{1}{\phi'\big(f^{-1}(1/x)\big)} \approx \tilde{I}_M(x) &\approx \frac{1}{x\tilde{\phi}(1/x)} \\ &\approx \frac{1}{x \phi(1/x)}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{1}{\phi'\big(f^{-1}(1/x)\big)} \approx \tilde{I}_M(x) &\approx \frac{1}{x\tilde{\phi}(1/x)} \\ &\approx \frac{1}{x \phi(1/x)}, \end{aligned} \end{align} $$
and (5.16) follows for all
![]() $A \leq A_M$
. Let us now consider
$A \leq A_M$
. Let us now consider
![]() $A> A_M$
. Observe that the functions
$A> A_M$
. Observe that the functions
 $$ \begin{align*} \bigg[\frac{A_M}{x_0},\frac{A}{x_0}\bigg] \ni x &\mapsto \frac{1}{x\phi(1/x)} \end{align*} $$
$$ \begin{align*} \bigg[\frac{A_M}{x_0},\frac{A}{x_0}\bigg] \ni x &\mapsto \frac{1}{x\phi(1/x)} \end{align*} $$
and
 $$ \begin{align*} \bigg[\frac{A_M}{x_0},\frac{A}{x_0}\bigg] \ni x &\mapsto \int_{\frac{x}{\phi'( f^{-1}(M/x))}}^{\infty} p(t,x) {\: \rm d} t \end{align*} $$
$$ \begin{align*} \bigg[\frac{A_M}{x_0},\frac{A}{x_0}\bigg] \ni x &\mapsto \int_{\frac{x}{\phi'( f^{-1}(M/x))}}^{\infty} p(t,x) {\: \rm d} t \end{align*} $$
are both positive and continuous; thus, they are bounded for each A. Therefore, at the possible expense of worsening the constant, we can conclude the proof of the proposition.
Proposition 5.6. Suppose that
![]() $b=0$
,
$b=0$
,
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0)$
for some
![]() $c \in (0,1]$
,
$c \in (0,1]$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $\alpha>0$
and that the Lévy measure
$\alpha>0$
and that the Lévy measure
![]() $\nu ({\mathrm {d}}x)$
is absolutely continuous with respect to the Lebesgue measure with a monotone density
$\nu ({\mathrm {d}}x)$
is absolutely continuous with respect to the Lebesgue measure with a monotone density
![]() $\nu (x)$
. Then there is
$\nu (x)$
. Then there is
![]() $\epsilon \in (0,1)$
such that for each
$\epsilon \in (0,1)$
such that for each
![]() $A>0$
, there is
$A>0$
, there is
![]() $C \geq 1$
such that for all
$C \geq 1$
such that for all
![]() $x < A/x_0$
,
$x < A/x_0$
,
 $$ \begin{align*} \int_0^{\frac{x}{\phi' ( f^{-1}(1/x) )}\epsilon} p(t,x) {\: \rm d} t \leq C \frac{1}{x\phi (1/x)}. \end{align*} $$
$$ \begin{align*} \int_0^{\frac{x}{\phi' ( f^{-1}(1/x) )}\epsilon} p(t,x) {\: \rm d} t \leq C \frac{1}{x\phi (1/x)}. \end{align*} $$
Proof. In view of (5.27), it is enough to show that for some
![]() $\epsilon \in (0, 1)$
and all
$\epsilon \in (0, 1)$
and all
![]() $A>0$
there is
$A>0$
there is
![]() $C \geq 1$
, such that for all
$C \geq 1$
, such that for all
![]() $x<A/x_0$
,
$x<A/x_0$
,
 $$ \begin{align} \int_0^{\frac{x}{\phi' ( f^{-1}(1/x) )}\epsilon} p(t,x) {\: \rm d} t \leq C \frac{1}{\phi' \big( f^{-1}(1/x) \big)}. \end{align} $$
$$ \begin{align} \int_0^{\frac{x}{\phi' ( f^{-1}(1/x) )}\epsilon} p(t,x) {\: \rm d} t \leq C \frac{1}{\phi' \big( f^{-1}(1/x) \big)}. \end{align} $$
Let
![]() $\epsilon \in (0, 1)$
and
$\epsilon \in (0, 1)$
and
 $$ \begin{align*} A = \min \bigg\{ 1,\frac{x_0}{f^*(x_0)} \bigg\}. \end{align*} $$
$$ \begin{align*} A = \min \bigg\{ 1,\frac{x_0}{f^*(x_0)} \bigg\}. \end{align*} $$
Suppose that
 $$ \begin{align} t \leq \frac{x}{\phi'\big(f^{-1}(1/x) \big)} \epsilon; \end{align} $$
$$ \begin{align} t \leq \frac{x}{\phi'\big(f^{-1}(1/x) \big)} \epsilon; \end{align} $$
that is,
 $$ \begin{align*} t \leq \frac{1}{\varphi^*\big(f^{-1}(1/x) \big)} \epsilon. \end{align*} $$
$$ \begin{align*} t \leq \frac{1}{\varphi^*\big(f^{-1}(1/x) \big)} \epsilon. \end{align*} $$
Hence, by monotonicity of
![]() $\varphi ^{-1}$
and
$\varphi ^{-1}$
and
![]() $\phi '$
,
$\phi '$
,
 $$ \begin{align*} x \geq \frac{1}{f^*\big(\varphi^{-1}(\epsilon/t)\big)} &= \frac{t}{\epsilon} \phi' \big( \varphi^{-1}(\epsilon/t) \big) \\ &\geq \frac{t}{\epsilon} \phi' \big( \varphi^{-1}(1/t) \big). \end{align*} $$
$$ \begin{align*} x \geq \frac{1}{f^*\big(\varphi^{-1}(\epsilon/t)\big)} &= \frac{t}{\epsilon} \phi' \big( \varphi^{-1}(\epsilon/t) \big) \\ &\geq \frac{t}{\epsilon} \phi' \big( \varphi^{-1}(1/t) \big). \end{align*} $$
By Proposition 4.3 and the scaling property of
![]() $\phi '$
, there are
$\phi '$
, there are
![]() $c \in (0,1]$
and
$c \in (0,1]$
and
![]() $C \geq 1$
such that
$C \geq 1$
such that
 $$ \begin{align*} x &\geq \frac{t}{\epsilon} \phi' \big( C\psi^{-1}(1/t) \big) \\ &\geq \frac{t}{\epsilon}cC^{\alpha-1} \phi' \big( \psi^{-1}(1/t) \big). \end{align*} $$
$$ \begin{align*} x &\geq \frac{t}{\epsilon} \phi' \big( C\psi^{-1}(1/t) \big) \\ &\geq \frac{t}{\epsilon}cC^{\alpha-1} \phi' \big( \psi^{-1}(1/t) \big). \end{align*} $$
Therefore, by taking
![]() $\epsilon = (2e)^{-1}cC^{\alpha -1}$
, we get
$\epsilon = (2e)^{-1}cC^{\alpha -1}$
, we get
 $$ \begin{align*} x \geq 2 e t \phi'\big(\psi^{-1}(1/t) \big). \end{align*} $$
$$ \begin{align*} x \geq 2 e t \phi'\big(\psi^{-1}(1/t) \big). \end{align*} $$
Since
![]() $\nu (x)$
is the monotone density of
$\nu (x)$
is the monotone density of
![]() $\nu ({\mathrm {d}} x)$
, by Theorem 4.8 we get
$\nu ({\mathrm {d}} x)$
, by Theorem 4.8 we get
 $$ \begin{align*} \int_0^{\frac{x}{\phi'( f^{-1}(1/x))} \epsilon} p(t,x) {\: \rm d} t &\lesssim \frac{\varphi(1/x)}{x} \bigg( \frac{x}{\phi'\big(f^{-1}(1/x)\big)} \bigg)^2. \end{align*} $$
$$ \begin{align*} \int_0^{\frac{x}{\phi'( f^{-1}(1/x))} \epsilon} p(t,x) {\: \rm d} t &\lesssim \frac{\varphi(1/x)}{x} \bigg( \frac{x}{\phi'\big(f^{-1}(1/x)\big)} \bigg)^2. \end{align*} $$
By (5.14),
![]() $f^{-1}(s) \gtrsim s$
for
$f^{-1}(s) \gtrsim s$
for
![]() $s>f^*(x_0)$
; thus, using (4.4),
$s>f^*(x_0)$
; thus, using (4.4),
 $$ \begin{align*} \frac{x\varphi(1/x)}{\phi' \big( f^{-1}(1/x) \big)} \leq \frac{\varphi(1/x)}{\varphi\big( f^{-1}(1/x) \big)} \lesssim 1, \end{align*} $$
$$ \begin{align*} \frac{x\varphi(1/x)}{\phi' \big( f^{-1}(1/x) \big)} \leq \frac{\varphi(1/x)}{\varphi\big( f^{-1}(1/x) \big)} \lesssim 1, \end{align*} $$
which entails (5.28). The extension to arbitrary A follows by continuity and positivity argument as in the proof of Proposition 5.4.
It is possible to get the same conclusion as in Proposition 5.6 without imposing the existence of the monotone density of
![]() $\nu ({\mathrm {d}} x)$
; however, instead we need to assume the weak upper scaling property in
$\nu ({\mathrm {d}} x)$
; however, instead we need to assume the weak upper scaling property in
![]() $-\phi ^{\prime \prime }$
.
$-\phi ^{\prime \prime }$
.
Proposition 5.7. Suppose that
![]() $b=0$
and
$b=0$
and
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0) \cap \mathrm {WUSC}(\beta -2,C,x_0)$
for some
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0) \cap \mathrm {WUSC}(\beta -2,C,x_0)$
for some
![]() $c \in (0,1]$
,
$c \in (0,1]$
,
![]() $C \geq 1$
,
$C \geq 1$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
 $\tfrac {1}{2}<\alpha \leq \beta <1$
. Then there is
$\tfrac {1}{2}<\alpha \leq \beta <1$
. Then there is
![]() $\epsilon \in (0, 1)$
such that for each
$\epsilon \in (0, 1)$
such that for each
![]() $A>0$
, there is
$A>0$
, there is
![]() $C_1 \geq 1$
, so that for all
$C_1 \geq 1$
, so that for all
![]() $x < A/x_0$
,
$x < A/x_0$
,
 $$ \begin{align} \int_0^{\frac{x}{\phi' ( f^{-1}(1/x) )} \epsilon} p(t,x) {\: \rm d} t \leq C_1 \frac{1}{x\phi (1/x)}. \end{align} $$
$$ \begin{align} \int_0^{\frac{x}{\phi' ( f^{-1}(1/x) )} \epsilon} p(t,x) {\: \rm d} t \leq C_1 \frac{1}{x\phi (1/x)}. \end{align} $$
Proof. Let
 $$ \begin{align*} A = \min\bigg\{1, \frac{x_0}{f^*(x_0)} \bigg\}. \end{align*} $$
$$ \begin{align*} A = \min\bigg\{1, \frac{x_0}{f^*(x_0)} \bigg\}. \end{align*} $$
By repeating the same reasoning as in the proof of Proposition 5.6, we can see that the condition
 $$ \begin{align*} t \leq \frac{x}{\phi' ( f^{-1}(1/x) )} \epsilon \end{align*} $$
$$ \begin{align*} t \leq \frac{x}{\phi' ( f^{-1}(1/x) )} \epsilon \end{align*} $$
implies
 $$ \begin{align*} x \geq 2 e t \phi'\big(\psi^{-1}(1/t) \big), \end{align*} $$
$$ \begin{align*} x \geq 2 e t \phi'\big(\psi^{-1}(1/t) \big), \end{align*} $$
for
![]() $\epsilon = (2e)^{-1} c C^{\alpha -1}$
. Therefore, we can apply Theorem 4.7 to get
$\epsilon = (2e)^{-1} c C^{\alpha -1}$
. Therefore, we can apply Theorem 4.7 to get
 $$ \begin{align} \int_0^{\frac{x}{\phi'( f^{-1}(1/x))} \epsilon} p(t,x) {\: \rm d} t \lesssim \varphi(1/x) \int_0^{\frac{x}{\phi'( f^{-1}(1/x))}\epsilon} t \varphi^{-1}(1/t) {\: \rm d} t, \end{align} $$
$$ \begin{align} \int_0^{\frac{x}{\phi'( f^{-1}(1/x))} \epsilon} p(t,x) {\: \rm d} t \lesssim \varphi(1/x) \int_0^{\frac{x}{\phi'( f^{-1}(1/x))}\epsilon} t \varphi^{-1}(1/t) {\: \rm d} t, \end{align} $$
where the implied constant may depend on
![]() $\epsilon $
. Since
$\epsilon $
. Since
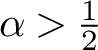 $\alpha> \tfrac {1}{2}$
, by Proposition 4.3, [Reference Aljančić and Aranđelović1, Theorem 3] and the doubling property of
$\alpha> \tfrac {1}{2}$
, by Proposition 4.3, [Reference Aljančić and Aranđelović1, Theorem 3] and the doubling property of
![]() $\varphi ^{-1}$
, we obtain
$\varphi ^{-1}$
, we obtain
 $$ \begin{align} \nonumber \int_0^{\frac{x}{\phi'( f^{-1}(1/x))}\epsilon} t\varphi^{-1}(1/t) {\: \rm d} t &\lesssim \bigg( \frac{x}{\phi'\big( f^{-1}(1/x) \big)} \bigg)^2 \varphi^{-1} \bigg( \frac{\phi' \big( f^{-1}(1/x) \big)}{ \epsilon x} \bigg) \\ &\lesssim \bigg( \frac{x}{\phi'\big( f^{-1}(1/x) \big)} \bigg)^2 \varphi^{-1} \bigg( \frac{\phi' \big( f^{-1}(1/x) \big)}{x} \bigg). \end{align} $$
$$ \begin{align} \nonumber \int_0^{\frac{x}{\phi'( f^{-1}(1/x))}\epsilon} t\varphi^{-1}(1/t) {\: \rm d} t &\lesssim \bigg( \frac{x}{\phi'\big( f^{-1}(1/x) \big)} \bigg)^2 \varphi^{-1} \bigg( \frac{\phi' \big( f^{-1}(1/x) \big)}{ \epsilon x} \bigg) \\ &\lesssim \bigg( \frac{x}{\phi'\big( f^{-1}(1/x) \big)} \bigg)^2 \varphi^{-1} \bigg( \frac{\phi' \big( f^{-1}(1/x) \big)}{x} \bigg). \end{align} $$
In view of (5.15), we have
 $$ \begin{align*} \frac{\phi' \big( f^{-1}(1/x) \big)}{x} &= \frac{\varphi^*\big(f^{-1}(1/x) \big)}{x f^*\big(f^{-1}(1/x)\big)} \\ &\lesssim \varphi^* \big( f^{-1}(1/x) \big); \end{align*} $$
$$ \begin{align*} \frac{\phi' \big( f^{-1}(1/x) \big)}{x} &= \frac{\varphi^*\big(f^{-1}(1/x) \big)}{x f^*\big(f^{-1}(1/x)\big)} \\ &\lesssim \varphi^* \big( f^{-1}(1/x) \big); \end{align*} $$
thus, by Proposition 4.3 and Remark 4.4,
 $$ \begin{align*} \frac{\varphi(1/x)x^2}{\phi'\big( f^{-1}(1/x) \big)} \varphi^{-1} \bigg( \frac{\phi' \big( f^{-1}(1/x) \big)}{x} \bigg) &\lesssim \frac{\varphi^*(1/x) x^2}{\phi'\big( f^{-1}(1/x) \big)} f^{-1}(1/x) \\ &= xf^{-1}(1/x) \frac{\varphi^*(1/x)}{\varphi^*\big(f^{-1}(1/x)\big)}. \end{align*} $$
$$ \begin{align*} \frac{\varphi(1/x)x^2}{\phi'\big( f^{-1}(1/x) \big)} \varphi^{-1} \bigg( \frac{\phi' \big( f^{-1}(1/x) \big)}{x} \bigg) &\lesssim \frac{\varphi^*(1/x) x^2}{\phi'\big( f^{-1}(1/x) \big)} f^{-1}(1/x) \\ &= xf^{-1}(1/x) \frac{\varphi^*(1/x)}{\varphi^*\big(f^{-1}(1/x)\big)}. \end{align*} $$
In view of Propositions 2.3 and 4.6, we have
![]() $f(s) \approx s$
for
$f(s) \approx s$
for
![]() $s> x_0$
; thus,
$s> x_0$
; thus,
![]() $f^{-1}(s) \approx s$
, for
$f^{-1}(s) \approx s$
, for
![]() $s> f^*(x_0)$
. Hence,
$s> f^*(x_0)$
. Hence,
 $$ \begin{align*} \frac{\varphi(1/x)x^2}{\phi'\big( f^{-1}(1/x) \big)} \varphi^{-1} \bigg( \frac{\phi' \big( f^{-1}(1/x) \big)}{x} \bigg) \lesssim 1. \end{align*} $$
$$ \begin{align*} \frac{\varphi(1/x)x^2}{\phi'\big( f^{-1}(1/x) \big)} \varphi^{-1} \bigg( \frac{\phi' \big( f^{-1}(1/x) \big)}{x} \bigg) \lesssim 1. \end{align*} $$
Therefore, by (5.31) and (5.32), we conclude that
 $$ \begin{align*} \int_0^{\frac{x}{\phi' ( f^{-1}(1/x) )} \epsilon} p(t,x) {\: \rm d} t \lesssim \frac{1}{\phi' \big( f^{-1}(1/x) \big)}, \end{align*} $$
$$ \begin{align*} \int_0^{\frac{x}{\phi' ( f^{-1}(1/x) )} \epsilon} p(t,x) {\: \rm d} t \lesssim \frac{1}{\phi' \big( f^{-1}(1/x) \big)}, \end{align*} $$
which, by Proposition 5.4 and (5.27), entails (5.30). The extension to arbitrary A follows by positivity and continuity argument.
Theorem 5.8. Let
![]() $\mathbf {T}$
be a subordinator with the Laplace exponent
$\mathbf {T}$
be a subordinator with the Laplace exponent
![]() $\phi $
. Suppose that
$\phi $
. Suppose that
for some
![]() $c \in (0,1]$
,
$c \in (0,1]$
,
![]() $C \geq 1$
,
$C \geq 1$
,
![]() $x_0 \geq 0$
and
$x_0 \geq 0$
and
![]() $0<\alpha \leq \beta <1$
. We assume that one of the following conditions holds:
$0<\alpha \leq \beta <1$
. We assume that one of the following conditions holds:
-
(i) The Lévy measure
 $\nu ({\mathrm {d}}x)$
is absolutely continuous with respect to the Lebesgue measure with monotone density
$\nu ({\mathrm {d}}x)$
is absolutely continuous with respect to the Lebesgue measure with monotone density
 $\nu (x)$
, or
$\nu (x)$
, or -
(ii)
 $\alpha> \tfrac 12$
.
$\alpha> \tfrac 12$
.
Then for each
![]() $A> 0$
there is
$A> 0$
there is
![]() $C_1 \geq 1$
such that for all
$C_1 \geq 1$
such that for all
![]() $x< A/x_0$
,
$x< A/x_0$
,
 $$ \begin{align*} C_1^{-1} \frac{1}{x\phi(1/x)} \leq G(x) \leq C_1 \frac{1}{x\phi(1/x)}. \end{align*} $$
$$ \begin{align*} C_1^{-1} \frac{1}{x\phi(1/x)} \leq G(x) \leq C_1 \frac{1}{x\phi(1/x)}. \end{align*} $$
Proof. By Corollary 2.7,
![]() $-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0) \cap \mathrm {WUSC}(\beta -2,C,x_0)$
. Let
$-\phi ^{\prime \prime } \in \mathrm {WLSC}(\alpha -2,c,x_0) \cap \mathrm {WUSC}(\beta -2,C,x_0)$
. Let
![]() $p(t, \: \cdot \:)$
be the transition density of
$p(t, \: \cdot \:)$
be the transition density of
![]() $T_t$
. In view of Propositions 5.4, 5.6 and 5.7 and (5.27), it is enough to show that for each
$T_t$
. In view of Propositions 5.4, 5.6 and 5.7 and (5.27), it is enough to show that for each
![]() $A> 0$
and
$A> 0$
and
![]() $\epsilon \in (0, 1)$
there is
$\epsilon \in (0, 1)$
there is
![]() $C_1> 0$
such that for all
$C_1> 0$
such that for all
![]() $x<A/x_0$
,
$x<A/x_0$
,
 $$ \begin{align} \int_{\frac{x}{\phi'( f^{-1}(1/x))}\epsilon}^{\frac{x}{\phi'( f^{-1}(1/x))}} p(t,x) {\: \rm d} t \leq C_1 \frac{1}{\phi' \big( f^{-1}(1/x) \big)}. \end{align} $$
$$ \begin{align} \int_{\frac{x}{\phi'( f^{-1}(1/x))}\epsilon}^{\frac{x}{\phi'( f^{-1}(1/x))}} p(t,x) {\: \rm d} t \leq C_1 \frac{1}{\phi' \big( f^{-1}(1/x) \big)}. \end{align} $$
By [Reference Grzywny and Szczypkowski23, Theorem 3.1], there is
![]() $t_0> 0$
such that for all
$t_0> 0$
such that for all
![]() $t \in (0, t_0)$
,
$t \in (0, t_0)$
,
If
![]() $x_0 = 0$
, then
$x_0 = 0$
, then
![]() $t_0 = \infty $
. We can take
$t_0 = \infty $
. We can take
 $$ \begin{align*} t_0 \geq \frac{x}{\phi'\big(f^{-1}(1/x)\big)}. \end{align*} $$
$$ \begin{align*} t_0 \geq \frac{x}{\phi'\big(f^{-1}(1/x)\big)}. \end{align*} $$
Therefore, by monotonicity of
![]() $\varphi ^{-1}$
, we get
$\varphi ^{-1}$
, we get
 $$ \begin{align*} \int_{\frac{x}{\phi'( f^{-1}(1/x))}\epsilon}^{\frac{x}{\phi'( f^{-1}(1/x))}} p(t,x) {\: \rm d} t &\lesssim \int_{\frac{x}{\phi'( f^{-1}(1/x))} \epsilon}^{\frac{x}{\phi'( f^{-1}(1/x))}} \varphi^{-1}(1/t) {\: \rm d} t \\ &\leq \frac{x}{\phi' \big( f^{-1}(1/x) \big)} \varphi^{-1} \bigg( \frac{\phi' \big( f^{-1}(1/x) \big)}{\epsilon x} \bigg). \end{align*} $$
$$ \begin{align*} \int_{\frac{x}{\phi'( f^{-1}(1/x))}\epsilon}^{\frac{x}{\phi'( f^{-1}(1/x))}} p(t,x) {\: \rm d} t &\lesssim \int_{\frac{x}{\phi'( f^{-1}(1/x))} \epsilon}^{\frac{x}{\phi'( f^{-1}(1/x))}} \varphi^{-1}(1/t) {\: \rm d} t \\ &\leq \frac{x}{\phi' \big( f^{-1}(1/x) \big)} \varphi^{-1} \bigg( \frac{\phi' \big( f^{-1}(1/x) \big)}{\epsilon x} \bigg). \end{align*} $$
By the doubling property of
![]() $\varphi ^{-1}$
, definition of f and Remark 4.4,
$\varphi ^{-1}$
, definition of f and Remark 4.4,
 $$ \begin{align*} \varphi^{-1} \bigg( \frac{\phi' \big( f^{-1}(1/x) \big)}{\epsilon x} \bigg) &\lesssim \varphi^{-1} \bigg( \frac{\phi' \big( f^{-1}(1/x) \big)}{x} \bigg) \\ &\leq f^{-1}(1/x) \\ &\lesssim \frac1x, \end{align*} $$
$$ \begin{align*} \varphi^{-1} \bigg( \frac{\phi' \big( f^{-1}(1/x) \big)}{\epsilon x} \bigg) &\lesssim \varphi^{-1} \bigg( \frac{\phi' \big( f^{-1}(1/x) \big)}{x} \bigg) \\ &\leq f^{-1}(1/x) \\ &\lesssim \frac1x, \end{align*} $$
since by the weak upper scaling property of
![]() $-\phi ^{\prime \prime }$
,
$-\phi ^{\prime \prime }$
,
![]() $f(s) \approx s$
for all
$f(s) \approx s$
for all
![]() $s> f^*(x_0)$
. Consequently, we obtain (5.33) and the theorem follows.
$s> f^*(x_0)$
. Consequently, we obtain (5.33) and the theorem follows.
Acknowledgements
We thank Professor Jerzy Zabczyk for drawing our attention to the problem considered in this article. The main results of this article were presented at the XV Probability Conference held from 21 to 25 May 2018 in Będlewo, Poland, and at the Semigroups of Operators: Theory and Applications Conference held from 30 September to 5 October 2018 in Kazimierz Dolny, Poland. We thank the organisers for the invitations. The authors were partially supported by the National Science Centre (Poland) (Grant No. 2016/23/B/ST1/01665).
Competing Interest
None.