2.1 Marked 3-manifold

By a open interval (respectively circle) we mean the image of $(0,1)$ (resp. the standard circle $S^1$ ) through an embedding of $[0,1]$ (resp. of $S^1$ ) into a manifold.

A priori two components of $\mathcal N$ might be mapped by i into the same component of $\mathcal N'$ .

If no component of $\mathcal N$ is a circle, we call $(M,\mathcal N)$ a circle-free marked 3-manifold.

It should be noted that while $M,\mathcal N$ are oriented, an $\mathcal N$ -tangle is not.

Definition 2.4. The stated skein module ${\mathscr S}(M,\mathcal N)$ of a marked 3-manifold $(M,\mathcal N)$ is the ${R}$ -module spanned by isotopy classes of stated $\mathcal N$ -tangles in M modulo the following relations:

(1)

(2)

(3)

(4)

In the above identities, the pictures depict the intersection of an $\mathcal N$ -tangle with a box $ S \times [-1,1]\hookrightarrow M$ , where S is a square and is identified with $S \times \{0\}$ . In this box, the $\mathcal N$ -tangle is described by its diagram coming from the standard projection onto S, which is the shadowed square. The orientation of S is counterclockwise, and the orientation of M is the given by that of S followed by the orientation of $[-1,1]$ , which is pointed to the reader. In Equations (3) and (4), the drawn edge of the square with its orientation is an oriented subarc of $\mathcal N$ . Besides, the signs indicate the states of each endpoint of the diagram. In all pictures in this paper, the framing is pointing towards the reader except in small neighbourhood of the boundary edges (the oriented arrows) where the framing twists by $\frac {\pi }{4}$ in order to become positively tangent to $\mathcal N$ (up to isotopy there is only one way to achieve this). Besides, the signs indicate the states of each endpoint of the diagram.

Identity (3) with $\epsilon =+, \nu =-$ is an easy consequence of the other relations (see [Reference Lê26, Lemma 2.3]), but we add it here for a complete list of values of cups (or trivial arcs).

It is clear that an embedding of pairs $i:(M,\mathcal N) \to (M' \mathcal N')$ induces an R-linear map $i_*: {\mathscr S}(M,N) \to {\mathscr S}(M', \mathcal N')$ , which depends only on the isotopy class of i.

Easy consequences of the defining relations are the following

(5)

(6)

2.2 Orientation inversion of components of $\mathcal N$

Recall $C(+)=-q^{-\frac {5}{2}}, C(-)=q^{-\frac {1}{2}}$ .

Proposition 2.6. Let e be a connected component of the marking set $\mathcal N$ of a marked 3-manifold $(M,\mathcal N)$ . Let ${\mathsf {inv}}_e(\mathcal N)$ be identical to $\mathcal N$ except that the orientation of e is reversed. There is an isomorphism of ${R}$ -modules ${\mathsf {inv}}_e:{\mathscr S}(M,\mathcal N)\to {\mathscr S}(M,{\mathsf {inv}}_e(\mathcal N))$ defined on a stated $\mathcal N$ -tangle $\alpha $ by:

(7) $$ \begin{align} {\mathsf{inv}}_e(\alpha)=\left(\prod_{u \in \alpha\cap e} C(u)\right) \overline{\alpha}, \end{align} $$

where $\overline {\alpha }$ is obtained from $\alpha $ by switching all the states of $\alpha \cap e$ and changing locally near e the framing of $\alpha $ by adding a positive half twist to each component touching e. Furthermore, applying twice ${\mathsf {inv}}_e$ gives the identity map ${\mathscr S}(M,\mathcal N)\to {\mathscr S}(M,\mathcal N)$ .

Proof. To show that ${\mathsf {inv}}_e$ is well defined, we check that Relations (3) and (4) are preserved.

Relation (3) is preserved, because from the definition and Equation (6),

Consider Relation (4). Apply ${\mathsf {inv}}_e$ to the left-hand side of Equation (4),

(8)

where the last identity follows from [Reference Lê26, Equ. (20)]. Apply ${\mathsf {inv}}_e$ to the left-hand side of Equation (4),

(9)

where the second equality follows from [Reference Lê26, Equ. (21)]. Comparing Equations (8) and (9), we see that Relation (4) is transformed into itself.

To prove the last statement observe that the total effect of applying twice ${\mathsf {inv}}_e$ is to multiply a $\mathcal N$ -tangle by $(-q^{-3})^{\# e\cap \alpha }$ and to add a full positive twist to each strand of $\alpha $ near e. But each additional framing is equivalent to multiplying $\alpha $ by $-q^{3}$ (see Equation (5)) so that the different factors compensate.

2.3 Manifolds defined up to strict isomorphisms

We will consider certain geometric operations on 3-manifolds, like cutting and gluing them along disks, or smoothing corners, which produce new manifolds defined up a diffeomorphisms only. Following [Reference TTQ and Sikora28], we use the following notion: A strict isomorphism class of marked 3-manifolds is a family of marked 3-manifolds $(M_i, \mathcal N_i), i \in I$ , equipped with diffeomorphisms $f_{ij} : (M_i,\mathcal N_i)\to (M_j,\mathcal N_j)$ for any two indices $i,j$ such that $f_{ii} = \mathrm {id}$ and $f_{jk} \circ f_{ij} = f_{ik}$ up to isotopy. For a strict isomorphism class of marked 3-manifolds, we can identify all ${R}$ -modules ${\mathscr S}(M_i, \mathcal N_i)$ via the isomorphisms $(f_{ij})_*$ . Note that gluing and cutting operations or smoothing corner operations produce strict isomorphism classes of marked 3-manifolds.

2.4 Boundary-oriented surface

When it is clear from context, we write $\mathfrak S$ instead of $(\mathfrak S,{ \mathsf {or}})$ . The orientation inversion map ${\mathsf {inv}}_e$ given by Proposition 2.6 shows that as R-modules ${\mathscr S}(\mathfrak S, { \mathsf {or}})\cong {\mathscr S}(\mathfrak S, { \mathsf {or}}_+)$ , where ${ \mathsf {or}}_+$ is the positive orientation of $\partial \mathfrak S$ .

The projection $ \mathfrak S \times (-1,1)\to \mathfrak S$ allows to consider diagrams of $\mathcal N$ -tangles.

Note that ‘generic immersion’ implies D meets $\partial \mathfrak S$ transversally and D has only a finite number of singularity, each is a double point lying in the interior of $\mathfrak S$ . The empty set is considered as a $\partial \mathfrak S$ -tangle diagram.

A $\partial \mathfrak S$ -tangle diagram D defines a $\mathcal N$ -isotopy class of $\mathcal N$ -tangle: Equip D with the vertical framing everywhere, except near $\partial \mathfrak S$ one turns the framing by $\pi /4$ to match the orientation ${ \mathsf {or}}$ of $\partial \mathfrak S$ . A $\partial \mathfrak S$ -tangle diagram is stated if it is equipped with a state, which is a map $\partial D \to \{ \pm \}$ . A state of D is increasing if for each boundary edge c of $\partial \mathfrak S$ , the states on e are increasing when traveling in the direction of ${ \mathsf {or}}$ .

A stated $\partial \mathfrak S$ -tangle diagram defines an element of ${\mathscr S}(\mathfrak S,{ \mathsf {or}})$ . Every $\mathcal N$ -isotopy class of stated $\mathcal N$ -tangles can be represented by stated $\partial \mathfrak S$ -tangle diagrams. Note that if D is a stated $\partial \mathfrak S$ -tangle diagram representing an element $x\in {\mathscr S}(\mathfrak S,{ \mathsf {or}})$ and e is a boundary edge of $\mathfrak S$ , then D, up to a power of $q^{1/2}$ , also represents the element ${\mathsf {inv}}_e(x)\in {\mathscr S}(\mathfrak S,{\mathsf {inv}}_e({ \mathsf {or}}))$ , where ${\mathsf {inv}}_e({ \mathsf {or}})$ is the same as ${ \mathsf {or}}$ except the orientation of e is reversed.

When $\partial \mathfrak S$ does not have a circle component, we call $\mathfrak S$ circle-free. In that case, ${\mathscr S}(\mathfrak S,{ \mathsf {or}})$ has an algebra structure defined in Section 4.

If $\mathfrak S$ is circle-free and ${ \mathsf {or}}={ \mathsf {or}}_+$ , then $\mathfrak S$ is known as a punctured bordered surface in [Reference Lê26, Reference Costantino and Le10, Reference Lê and Yu29, Reference Lê and Yu30] and ${\mathscr S}(\mathfrak S,{ \mathsf {or}})$ is studied intensively there.

2.5 Half-ideal slit of surface

A $\partial \mathfrak S$ -tangle diagram is simple if it has neither double points nor trivial components. Here, a component is trivial if it is a circle bounding a disk in $\mathfrak S$ or it is an arc homotopic relative its endpoints to a subset of $\partial \mathfrak S$ . By [Reference Lê26, Theorem 2.8], if $\mathfrak S$ is circle-free, then ${\mathscr S}(\mathfrak S,{ \mathsf {or}})$ is free over R with basis the set $\mathcal B(\mathfrak S,{ \mathsf {or}})$ of all isotopy classes of increasingly stated simple diagrams. We want to consider the case when $\partial \mathfrak S$ has a circle component. It turns out that when $\mathfrak S$ is noncompact and connected we can show that ${\mathscr S}(\mathfrak S,{ \mathsf {or}})$ is free over R and find a free basis of it by eliminating the circles.

Assume $\alpha $ is a half-ideal arc connecting an ideal point p and a point of a boundary component $c\subset \partial \mathfrak S$ . Note that p can be an interior ideal point or a boundary ideal point, and c can be a boundary edge or a boundary circle. The $\alpha $ -slit of $(\mathfrak S,{ \mathsf {or}})$ is the boundary oriented surface $(\mathfrak S', { \mathsf {or}}')$ , where $\mathfrak S':=\mathfrak S\setminus \alpha $ and ${ \mathsf {or}}'$ is the restriction of ${ \mathsf {or}}$ ; see Figure 1. The whole interval $\alpha $ is an ideal point of $\mathfrak S'$ . We also call $(\mathfrak S', { \mathsf {or}}')$ a half-ideal slit of $({\mathfrak S}, \mathsf {or})$ breaking c when we don’t want to mention $\alpha $ . In $\mathfrak S'$ , the remnant of c is never a circle.

Figure 1 A half-ideal slit breaking c, with an interior ideal point.

Proof. Using the isomorphism ${\mathsf {inv}}_e$ , we can assume that ${ \mathsf {or}}$ is the positive orientation. Relation (4) can be rewritten as

(10)

which shows that any $x\in {\mathscr S}(\mathfrak S, { \mathsf {or}})$ is a linear combination of stated $\partial \mathfrak S$ -tangle diagrams not meeting $\alpha $ . Hence, the map $\iota _*$ is surjective. We will construct an inverse of $\iota _*$ .

Claim. ${\mathscr S}(\mathfrak S,{ \mathsf {or}})$ is the free span of isotopy classes of stated $\partial \mathfrak S$ -tangle diagrams modulo the four relations (1)–(4). In fact, isotopy classes of stated $\partial \mathfrak S$ -tangles are given by isotopy classed of stated $\partial \mathfrak S$ -tangle diagrams modulo the Reidemeister moves of type II and type III defined in [Reference Lickorish31]. Thus, ${\mathscr S}(\mathfrak S,{ \mathsf {or}})$ is the free span of isotopy classes of stated $\partial \mathfrak S$ -tangle diagrams modulo the four relations (1)–(4) and the Reidemeister moves of type II and type III. By [Reference Lickorish31, Lemma 3.3], a Reidemeister move of type II or III can be realised by Relations (1) and (2). Hence, we have the claim.

For a concrete stated $\partial \mathfrak S$ -tangle diagram D intersecting $\alpha $ transversally in k points define $f(D) \in {\mathscr S}(\mathfrak S', { \mathsf {or}}')$ by repeatedly applying identity (10):

(11)

Here, ‘concrete’ simply means to we don’t identify D with its isotopy class in $\mathfrak S$ . Let us show that f depends only on the isotopy class of D. It is enough to show that f is invariant under the moves M1 and M2 given in Figure 2.

Figure 2 Moves M1 and M2 for isotopy of D.

Consider move M1. Using Equation (11) and the values of the cups given by Equation (3),

Consider move M2. Using Equation (11) then move M1, and then Equation (10), we have

More in general, if in D there are some vertical strands between the cup shaped strand and c, then we first apply Equation (11) to these strands to reduce to the previous case pictured above.

Thus, f is a well-defined R-linear map. From the definition $f \circ \iota _*=\mathrm {id}$ . It follows that $\iota _*$ is injective, whence bijective.

When $\mathfrak S$ is noncompact and connected, for a circle boundary component c there is a half-ideal arc $\alpha $ with endpoint in c, and the $\alpha $ -slit of $\mathfrak S$ is still connected. Hence, we have

2.6 Compact slit

Corollary 2.11 provides a free basis of the ${R}$ -module ${\mathscr S}(\mathfrak S)$ under the hypothesis that $\mathfrak S$ is noncompact and connected. We will show that when $\mathfrak S$ is compact ${\mathscr S}(\mathfrak S,{ \mathsf {or}})$ is a nice quotient of ${\mathscr S}(\mathfrak S',{ \mathsf {or}}')$ , where $\mathfrak S'$ is noncompact. Besides, Example 2.14 will show that in general ${\mathscr S}(\mathfrak S,{ \mathsf {or}})$ is not free over ${R}$ , unlike the case when $\mathfrak S$ is noncompact and connected.

Theorem 2.13. Suppose $(\mathfrak S,{ \mathsf {or}})$ is a boundary-oriented surface and $\alpha $ is a $\partial \mathfrak S$ -arc. Let $\mathfrak S'=\mathfrak S\setminus \alpha $ and ${ \mathsf {or}}'$ be the restriction of ${ \mathsf {or}}$ ; see Figure 3. Then ${\mathscr S}(\mathfrak S,{ \mathsf {or}})={\mathscr S}(\mathfrak S',{ \mathsf {or}}')/\sim $ , where $\sim $ is the equivalence relation given in Figure 3.

Figure 3 Left: slitting along a properly embedding arc. Right: the equivalence relation. All circular bold arcs might be in the same component of $\partial \mathfrak S$ .

Proof. The proof is similar and uses many ingredients of the proof of Theorem 2.10. Again, using ${\mathsf {inv}}_e$ we can assume that the orientation ${ \mathsf {or}}$ is positive.

The map induced from the embedding $ (\mathfrak S', { \mathsf {or}}') \hookrightarrow (\mathfrak S, { \mathsf {or}})$ clearly descends to an R-linear map $\pi :{\mathscr S}(\mathfrak S',{ \mathsf {or}}')/\sim \to {\mathscr S}(\mathfrak S,{ \mathsf {or}})$ . Identity (10) shows that $\pi $ is surjective. We will define an inverse of it. Orient $\alpha $ , for example, assuming its direction is pointing to the right in Figure 3.

Let D be a concrete stated $\partial \mathfrak S$ -tangle diagram. Define $f(D)$ by exactly the same formula (11), except now the values should be in ${\mathscr S}(\mathfrak S',{ \mathsf {or}}')/\sim $ . Note that in defining f we use the right circular arc (determined by the direction of $\alpha $ ), not the left one.

Two stated $\partial \mathfrak S$ -tangle diagrams give isotopic stated $\partial \mathfrak S$ -tangles if and only if they are related by moves M1, M2 and in addition move M3:

From the proof of Theorem 2.10, we know f is invariant under moves M1 and M2, even without the relation $\sim $ . For move M3, we will need relation $\sim $ . Using the definition of f then relation $\sim $ ,

Thus, f gives a well-defined map ${\mathscr S}(\mathfrak S, { \mathsf {or}}) \to {\mathscr S}(\mathfrak S',{ \mathsf {or}}')/\sim $ which is a left inverse of $\pi $ . It follows that $\pi $ is injective, whence bijective.

2.7 Examples, torsion in case of compact surfaces

An n-gon ${\mathbb P}_n$ is the standard closed disk with n points on its boundary removed.

Let ${\mathbb P}_{n,k}$ be obtained from ${\mathbb P}_n$ be removing k interior points. In particular, ${\mathbb P}_{0,k}$ is the closed disk with k interior points removed. In this subsection, we consider ${\mathbb P}_{n,k}$ as a boundary-oriented surface, where the orientation of the boundary is positive.

In [Reference Lê26], it is proved that ${\mathscr S}({\mathbb P}_{1})\cong R$ via the map whose inverse is $r \to r \emptyset $ . We proved in [Reference Costantino and Le10] that ${\mathscr S}({\mathbb P}_2)$ has a natural structure of a Hopf algebra, and as Hopf algebras it is isomorphic to the quantised coordinate algebra ${\mathcal O}_{q^2}(\mathrm {SL}(2))$ of the group $SL_2(R)$ . See also [Reference Korinman and Quesney22].

By Theorem 2.11, using a half-ideal slit on ${\mathbb P}_{n,k+1}$ we get an R-linear isomorphism

(12) $$ \begin{align} {\mathscr S}({\mathbb P}_{n,k+1} ) \cong {\mathscr S}({\mathbb P}_{n+1,k}). \end{align} $$

In particular, we have the following ${R}$ -linear isomorphisms:

$$ \begin{align*}{\mathscr S}({\mathbb P}_{0,1})\cong {{\mathscr S}}({\mathbb P}_{1,0} ) \cong R, \quad {\mathscr S}({\mathbb P}_{1,1})\cong {\mathscr S}({\mathbb P}_{2}) \cong {\mathcal O}_{q^2}(\mathrm{SL}(2)). \end{align*} $$

If $S_{2,1}$ is the result of removing two small open disks and one point from the sphere, with positive orientation, then by using two half-ideal slits we get ${R}$ -linear isomorphism

(13) $$ \begin{align} {\mathscr S}(S_{2,1})={\mathscr S}({\mathbb P}_2)={\mathcal O}_{q^2}(\mathrm{SL}(2)). \end{align} $$

2.8 Circle boundary element

Proof. Using (10), we have

where in the second equality we used the values of cups given by Equation (3).

2.9 Cutting homomorphism

Two boundary components of a boundary-oriented surface are of the same type if they are both circles or both boundary edges. Let $c_1, c_2$ be two boundary components of the same type of a boundary-oriented surface $(\mathfrak S',{ \mathsf {or}}')$ . Assume $c_1$ and $c_2$ have opposite orientations, that is, one positive and one negative. Let $\mathfrak S= \mathfrak S'/(c_1=c_2)$ where we identify $c_1$ with $c_2$ via an orientation preserving diffeomorphism. Let ${ \mathsf {or}}$ be the orientation of $\partial \mathfrak S$ which is induced from ${ \mathsf {or}}'$ , and $\mathrm {pr}: \mathfrak S' \to {\mathfrak S}$ be the natural projection. Denote $c= \mathrm {pr}(c_1)= \mathrm {pr}(c_2)$ . If $c_1, c_2$ are boundary edges, then c is an oriented ideal arc of $\mathfrak S$ ; otherwise, c is a an oriented simple closed curve in the interior of $\mathfrak S$ .

In this situation, we also say that $(\mathfrak S',{ \mathsf {or}}')$ is a result of cutting $(\mathfrak S,{ \mathsf {or}})$ along c. For an example, see Figure 4, where we also give an idea of how the map $\mathsf {Cut}_c$ is defined.

Figure 4 Left: Cutting along an interior ideal arc c. Right: The map $\mathsf {Cut}_c$ . The case when c is a circle is similar.

Suppose $\alpha $ is a stated $\partial \mathfrak S$ -tangle diagram transversal to c. Then $\tilde \alpha :=\mathrm {pr}^{-1}(\alpha )$ is a $\partial \mathfrak S'$ -tangle diagram which inherits states from $\alpha $ at all boundary points, except for those in $c_1 \cup c_2$ . For every $\boldsymbol {\epsilon }: \alpha \cap c \to \{\pm \}$ , let $\tilde \alpha (\boldsymbol {\epsilon })$ be the stated $\partial \mathfrak S'$ -tangle diagram whose states on $c_1 \cup c_2$ are the lift of $\boldsymbol {\epsilon }$ , that is, the state at both points in $\mathrm {pr}^{-1}(u)$ is $\boldsymbol {\epsilon }(u)$ .

Here is an extension of [Reference Lê26, Theorem 1], where the case c is an ideal arc is proved.

Theorem 2.16. Assume $(\mathfrak S',{ \mathsf {or}}')$ is a result of cutting $(\mathfrak S,{ \mathsf {or}})$ along c as above, where c is either an interior oriented ideal arc or an interior oriented simple loop.

There exists a unique ${R}$ -linear homomorphism $\mathsf {Cut}_c :{\mathscr S}(\mathfrak S,{ \mathsf {or}}) \to {\mathscr S}(\mathfrak S',{ \mathsf {or}}')$ such that if $\alpha $ is a stated $\partial \mathfrak S$ -tangle diagram transversal to c, then

(14) $$ \begin{align} \mathsf{Cut}_c(\alpha) = \sum_{\boldsymbol{\epsilon}: \alpha \cap c \to \{ \pm \}} \tilde \alpha(\boldsymbol{\epsilon}) \in {\mathscr S}(\mathfrak S'). \end{align} $$

Proof. The proof for the case when c is an ideal arc is given in [Reference Lê26] and can be applied also to the case when c is a circle: For a concrete stated $\partial \mathfrak S$ -tangle diagram D define $\mathsf {Cut}_c \in {\mathscr S}(\mathfrak S', { \mathsf {or}}')$ by the right-hand side of Equation (14). We need to show that $\mathsf {Cut}_c(D)$ depends only on the isotopy class of D. It is enough show that $\mathsf {Cut}_c(D)$ is invariant under the move

This is proved in [Reference Lê26] for the case when c is an ideal arc, but the proof there involves only a small part of c and applies as well in the case when c is a circle.

From the definition, we see that if c and $c'$ are disjoint, then

(15) $$ \begin{align} \mathsf{Cut}_{c} \circ \mathsf{Cut}_{c'} = \mathsf{Cut}_{c'} \circ \mathsf{Cut}_{c}. \end{align} $$

Remark 2.17. In [Reference Lê26], it is proved that if $\mathfrak S$ is circle-free, then $\mathsf {Cut}_c$ is injective. However, cutting along a circle might not be injective. In fact, let $\mathfrak S$ be an arbitrary circle-free boundary-oriented surface and c be a trivial simple loop in $\mathfrak S$ . Cutting $\mathfrak S$ along c we get $\mathfrak S'=\mathfrak S_1 \sqcup \mathfrak S_2$ , where $\mathfrak S_2$ is a closed disk. By Example 2.14, as R-modules ${\mathscr S}(\mathfrak S_2)= R/(q^2+1)$ . The cutting homomorphism

$$ \begin{align*}\mathsf{Cut}_c: {\mathscr S}(\mathfrak S) \to {\mathscr S}(\mathfrak S') = {\mathscr S}(\mathfrak S_1) \otimes_R (R/(q^2+1))\end{align*} $$

is not injective since it maps the empty element $\emptyset $ , which is an element of the free R-basis $\mathcal B(\mathfrak S)$ of ${\mathscr S}(\mathfrak S)$ , to a torsion element killed by $q^2+1$ .

2.10 Cutting for $3$ -manifolds

Cutting for 3-manifolds is similar. The case involving a boundary edge is discussed in [Reference Bloomquist and Lê3, Reference Lê and Yu29]. Let us consider the general case.

Suppose $(M', \mathcal N')$ is a marked 3-manifold, not necessarily connected. Assume $c_1, c_2\subset \partial M'$ are two distinct components of $\mathcal N'$ of the same type (i.e., both arcs or circles), and let $D_1,D_2\subset \partial M'$ be closed disjoint regular neighbourhoods of $c_1$ and $c_2$ . This means, if $c_1, c_2$ are boundary edges then each $D_i$ is a closed disk containing $c_i$ in its interior; otherwise, each $D_i$ is a closed annulus containing $c_i$ in its interior and deformation retracts to $c_i$ . We assume that $D_i\cap \mathcal N= c_i$ . Choose an orientation-reversing diffeomophism $\phi :D_1 \to D_2$ such that $\phi (c_1)=c_2$ as oriented arcs or circles. Let M be obtained from $M'$ by gluing $D_1$ to $D_2$ via $\phi $ and $\mathrm {pr}:M' \to M$ be the canonical projection. Denote $c= \mathrm {pr}(c_1) =\mathrm {pr}( c_2)$ and $D= \mathrm {pr}(D_1)= \mathrm {pr}(D_2)$ . Orient c using the orientation of $c_1$ (or $c_2$ ). Consider the marked 3-manifold $(M,\mathcal N)$ , where $\mathcal N = \mathrm {pr}^{-1}( \mathcal N' \setminus ( c_1 \cup c_2))$ .

An $\mathcal N$ -tangle $\alpha $ in M is $(D,c)$ -transversal if

• • $\alpha $ is transversal to D,

• • $\alpha \cap D=\alpha \cap c$ , and

• • the framing at every point of $\alpha \cap c$ is a positive tangent vector of c.

It is easy to see that every $\mathcal N$ -tangle is $\mathcal N$ -isotopic to one which is $(D,c)$ -transversal.

Suppose $\alpha $ is a $(D,c)$ -transversal stated $\mathcal N$ -tangle. Then $\tilde \alpha :=\mathrm {pr}^{-1}(\alpha )$ is an $\mathcal N'$ -tangle which is stated at every boundary point except for the boundary points in $c_1\cup c_2$ . For every map $\boldsymbol {\epsilon }: \alpha \cap c \to \{\pm \}$ , let $\tilde \alpha (\boldsymbol {\epsilon })$ be the stated $\mathcal N'$ -tangle, where the state of a boundary point $u\in N \cup N'$ is $ \boldsymbol {\epsilon }(\mathrm {pr}(u))$ .

Theorem 2.18. With the above assumptions, there is a unique R-linear homomorphism $\mathsf {Cut}_{D,c}: {\mathscr S}(M,\mathcal N) \to {\mathscr S}(M', \mathcal N')$ such that for every $(D,c)$ -transversal stated $\mathcal N$ -tangle $\alpha $ ,

$$ \begin{align*}\mathsf{Cut}_{D,c}(\alpha)= \sum_{\boldsymbol{\epsilon}: \alpha \cap c \to \{\pm \}} \tilde \alpha(\boldsymbol{\epsilon}), \quad \text{identity in } \ {\mathscr S}(M', \mathcal N'). \end{align*} $$

Furthermore if $(D',c')$ is another pair as above so that $D\cap D'=\emptyset $ , then $\mathsf {Cut}_{D,c}\circ \mathsf {Cut}_{D',c'}=\mathsf {Cut}_{D',c'}\circ \mathsf {Cut}_{D,c}$ .

By Example 2.14, we have the following:

3.1 Pattern in a disk

Let D be the standard closed disk and $W_n\subset \partial D$ be a set of $2n$ points in its boundary. A $W_n$ -tangle diagram T on D is a generic embedding of a compact nonoriented one-dimensional manifold into D such that $\partial T= W_n$ , with the usual under/overcrossing information at every double point like in a knot diagram. We consider T as a framed tangle in $\tilde D:=D \times (-1,1)$ , with vertical framing everywhere. Define $\mathsf {TL}_{n}$ as the ${\mathbb C}$ -module generated by isotopy classes of $W_n$ -tangle diagrams modulo the skein relations (1) and (2). Note that $\mathsf {TL}_n$ , known as the Temperley–Lieb algebra, depends on q but we suppress q in the notation. An element $x\in \mathsf {TL}_n$ is called a pattern.

Suppose $x= \sum c_i T_i\in \mathsf {TL}_n$ , where each $T_i$ is a $W_n$ -tangle diagram. An element $\alpha \in {\mathscr S}(M,\mathcal N)$ is a closure of x if there is an embedding of the thickening $\tilde D:=D \times (-1,1)$ into M such that $\alpha $ has a presentation $\alpha = \sum c_i \alpha _i$ , where each $\alpha _i$ is a stated $\mathcal N$ -tangle and $\alpha _i\cap \tilde D= T_i$ , and outside $ \tilde D$ all the tangles $\alpha _i$ are the same. If we denote the common outside part by $\beta $ , then we say that $\alpha $ is the result of closing x by $\beta $ .

For each $n \ge 0$ the Jones–Wenzl idempotent is the element $f_n\in \mathsf {TL}_n$ , denoted by a box enclosing n and defined by

where ${\mathrm {Sym}}_n$ is the group of permutations of n objects, and $\sigma _+$ is the positive braid with minimal number of crossing representing the permutation $\sigma $ , and $\ell (\sigma )$ is the length of $\sigma $ . For the definition $f_n$ , we must assume that $[n]_q!$ is invertible in ${R}$ . It is known that (see [Reference Lickorish31, Lemma 13.2]) $f_n$ has the nonreturnable property:

(16)

where the cap connect two consecutive right boundary points of the box.

Let $\mathring {\mathbb A}=(-1,1)\times S^1$ be the open annulus. The core of $\mathring {\mathbb A}$ is the circle $a=\{0\} \times S^1$ . The skein algebra ${\mathscr S}(\mathring {\mathbb A})$ is equal to the ring $R[a]$ of polynomials in a. By [Reference Lickorish31, Lemma 13.2], in ${\mathscr S}(\mathring {\mathbb A})$ we have

(17)

where $S_n(x)\in \mathbb Z[x]$ is the Chebychev polynomial of second type defined inductively by

$$ \begin{align*}S_0(x)=1, S_1(x)= x, S_n(x) = x S_{n-1}(x) - S_{n-2}(x) \ \text{for} \ n \ge 2.\end{align*} $$

3.2 Connected sum

For $i=1,2$ , assume ${\mathbf M}_i=(M_i,\mathcal N_i)$ is a connected marked 3-manifold. Recall that the connected sum $M_1 \# M_2$ is obtained by first removing the interior of a small ball $B_i$ from $M_i$ to obtain $M^{\prime }_i$ then gluing $M^{\prime }_1$ with $M^{\prime }_2$ along the boundaries of $B_i$ . Let ${\mathbf M}_1 \# {\mathbf M}_2= (M_1\# M_2, \mathcal N_1 \cup \mathcal N_2)$ . Define

$$ \begin{align*}\Psi_{{\mathbf M}_1, {\mathbf M}_2;q^{1/2}} : {\mathscr S}_{q^{1/2}}({\mathbf M}_1) \otimes {\mathscr S}_{q^{1/2}}({\mathbf M}_2) \to {\mathscr S}_{q^{1/2}}({\mathbf M}_1 \# {\mathbf M}_2)\end{align*} $$

so that if $\alpha _i\subset M_i$ is a framed tangle not meeting $B_i$ , then

$$ \begin{align*} \Psi_{{\mathbf M}_1, {\mathbf M}_2;q^{1/2}}(\alpha_1 \otimes \alpha_2) = \alpha_1 \cup \alpha_2, \ \text{as an element of } {\mathscr S}_{q^{1/2}}({\mathbf M}_1 \# {\mathbf M}_2). \end{align*} $$

It is easy to see that $\Psi _{{\mathbf M}_1, {\mathbf M}_2;q^{1/2}}$ is a well-defined ${\mathbb C}$ -linear homomorphism.

J. Pryztycki [Reference Przytycki32] proved that if q is not a root of 1 and $\mathcal N_1=\mathcal N_2=\emptyset $ , then $\Psi _{{\mathbf M}_1, {\mathbf M}_2;q^{1/2}}$ is bijective. The proof can be easily extended to the case of arbitrary $\mathcal N_1$ and $\mathcal N_2$ using Proposition 4.10. Here, we show that in general the map $\Psi _{{\mathbf M}_1, {\mathbf M}_2;q^{1/2}}$ is not injective.

Assume q is a root of 1. For a marked 3-manifold ${\mathbf M}=(M,\mathcal N)$ , let $F_{q^{1/2}}({\mathbf M})$ be the ${\mathbb C}$ -subspace of ${\mathscr S}_{q^{1/2}}({\mathbf M})$ spanned by all closures the Jones–Wenzl idempotent $f_{N-1}$ , where $N = \mathrm {ord}(q^4)$ .

In particular, if $N=2$ we get the following:

Corollary 3.3. Suppose $\mathrm {ord}(q^4)=2$ . If for $i=1,2$ $\alpha _i\subset {\mathbf M}_i$ is a nonempty $\mathcal N_i$ -tangle, then

$$ \begin{align*}\Psi_{{\mathbf M}_1, {\mathbf M}_2;q^{1/2}}(\alpha_1\sqcup \alpha_2)=0.\end{align*} $$

We expect that if $\mathrm {ord}(q^4)>1$ and $\pi _1(M)$ is nontrivial, then $F_{q^{1/2}}(M) \neq 0$ . This is true at least for thickened surfaces:

A special useful case is when $M_1, M_2$ are the thickening of the annulus $\mathring {\mathbb A}= (0,1)\times S^1$ .

3.3 Empty tangle element

If $\mathfrak S$ is a circle-free boundary-oriented surface, then the empty tangle, being an element of the free basis $\mathcal B(\mathfrak S)$ , is not zero and moreover serves as the unit of the algebra structure.

The situation can change for 3-manifolds. Suppose $(M,\mathcal N)$ is a marked 3-manifold. We say that an embedded sphere $S=S^2 \hookrightarrow M$ lying in the interior of M is marking separating if there there is a properly embedded path $a: [0,1] \hookrightarrow M$ transversal to S and meeting S at exactly one point such that $a(0), a(1) \in \mathcal N$ .

3.4 Noninjectivity of the cutting homomorphism

For surfaces, the cutting homomorphism along an ideal arc is always injective; see [Reference Lê26].

Theorem 3.9 (Proof in Subsection 3.7).

Suppose q is a complex root of 1 with ${\mathrm {ord}(q^4)>1}$ . There exists a compact 3-manifold M, a properly embedding disk $E \hookrightarrow M$ and an oriented open interval $e\subset E$ such that the cutting homomorphism

$$ \begin{align*}\mathsf{Cut}_{E,e}: {\mathscr S}_{q^{1/2}}(M) \to {\mathscr S}_{q^{1/2}}(M', \mathcal N')\end{align*} $$

is not injective. Here, $(M', \mathcal N')$ is the result of cutting $(M, \emptyset )$ along $(E,e')$ .

3.5 Noninjectivity of adding a marking

Let ${\mathbf M}=(M,\mathcal N)$ be a marked 3-manifold where M is connected. Choose a closed ball B in the interior of M. Let $\hat {{\mathbf M}} = (\hat M, \widehat {\mathcal N})$ , where $\hat M = M \setminus \mathring B$ and $\widehat {\mathcal N}= \mathcal N \cup c$ , where c is an open interval on $\partial B$ . Define the R-linear map $\Gamma _{\mathbf M}: {\mathscr S}({\mathbf M}) \to {\mathscr S}(\hat {{\mathbf M}})$ as follows. Suppose $\alpha \in {\mathscr S}({\mathbf M})$ is represented by a stated $\mathcal N$ -tangle T. By an isotopy, we can assume T does not meet B. Then $\Gamma _{\mathbf M}(\alpha )=T$ as an element ${\mathscr S}(\hat {{\mathbf M}})$ . It is easy to see that $\Gamma $ is well defined. This construction is closely related to the notion of quantum fundamental group discussed in Subsection 6.3.

Proof. We present here two independent proofs.

(i) Let M be the closed 3-ball and $\mathcal N$ be an open interval on $\partial M$ . The $\hat M= S^2 \times [1,2]$ and $\widehat {\mathcal N}$ consisting of two intervals $e_1, e_2$ , where $e_i \subset S^2 \times \{i\}$ . Clearly, the sphere $S^2 \times \{3/2\}$ is separating $e_1$ and $e_2$ . By Theorem 3.8, the empty tangle is equal to 0 in ${\mathscr S}_{q^{1/2}}(\hat {{\mathbf M}})$ . Since ${\mathbf M}$ is the thickening of the monogon ${\mathbb P}_1$ , the empty tangle is not 0 in ${\mathscr S}_{q^{1/2}}({\mathbf M})= {\mathbb C}$ .

(ii) The following proof gives a much larger class of examples. First, assume ${\mathbf M}$ be any marked 3-manifold. We have the following commutative diagram

(18)

where the lower map is the isomorphism of Theorem 6.10. Corollary 3.6 showed that there are examples when $\Psi _{{\mathbf M}, {\mathbf M};q^{1/2}}$ is not injective. In that case, the commutative diagram implies that $\Gamma _{{\mathbf M}} \otimes \Gamma _{{\mathbf M}}$ is not injective, which in turns, implies that $\Gamma _{{\mathbf M}}$ is not injective.

3.6 Noninjectivity of the Chebyshev–Frobenius homomorphism

Suppose $q^{1/2}$ is a root of 1 and $N= \mathrm {ord} (q^4)$ . Let $\epsilon := q^{N^2/2}$ . Note that $\epsilon ^8=1$ .

The Chebyshev polynomial of first type $T_n(x)=\sum _{i=0}^N c_i x^i\in \mathbb Z[x]$ is defined by the identity

$$ \begin{align*}T_n(u+u^{-1}) = u^n + u^{-n}.\end{align*} $$

For a framed knot $\alpha $ in an oriented 3-manifold M, define the $T_N$ -threading of $\alpha $ by

$$ \begin{align*}\alpha^{(T_N)} = \sum_{i=0}^N c_i \alpha^{(i)},\ \text{considered as an element of } \ {\mathscr S}_{q^{1/2}}(M),\end{align*} $$

where $\alpha ^{(i)}$ is i parallel push-offs (using the framing) of $\alpha $ lying in a small neighbourhood of $\alpha $ . When $\alpha $ is the disjoint union of k framed knots, $\alpha = \sqcup _{i=1}^k \alpha _i$ , its threading is defined by linear extrapolation:

$$ \begin{align*}\alpha^{(T_N)} = \alpha_1^{(T_N)} \cup \dots \cup \alpha_k^{(T_N)}:= \sum_{i_1,\dots, i_k=0}^N c_{i_1} \dots c_{i_k} \left [ \alpha_{1}^{(i_1)} \cup \dots \cup \alpha_{k}^{(i_k)} \right]\!.\end{align*} $$

The Chebyshev–Frobenius homomorphism is the ${\mathbb C}$ -linear map

$$ \begin{align*}\Phi_{q^{1/2}}: {\mathscr S}_\epsilon (M) \to {\mathscr S}_{q^{1/2}} (M)\end{align*} $$

defined so that if $x\in {\mathscr S}_\epsilon (M)$ is presented by disjoint union $\alpha $ of framed knots, then

(19) $$ \begin{align} \Phi_{q^{1/2}}(\alpha) = \alpha^{(T_N)} \quad \text{considered as an element of } \ {\mathscr S}_{q^{1/2}}(M). \end{align} $$

The well definedness of $\Phi _{q^{1/2}}$ is not an easy fact. When M is a thickened surface without boundary Bonahon and Wong [Reference Bonahon and Wong8] showed that $\Phi _{q^{1/2}}$ is well defined. The result is extended to all 3-manifolds in [Reference Lê25]. For the case of marked 3-manifolds, see [Reference Bloomquist and Lê3, Reference Lê and Paprocki27], where the definition of $\Phi _{q^{1/2}}$ needs to be modified for arcs. When M is the thickening of a surface, $\mathfrak S$ without boundary $\Phi _{q^{1/2}}$ is injective as it maps the basis $\mathcal B(\mathfrak S)$ of ${\mathscr S}_\epsilon (\mathfrak S)$ injectively into a basis of ${\mathscr S}_{q^{1/2}}(\mathfrak S)$ . Here, we show that $\Phi _{q^{1/2}}$ is not injective in general.

Proof. Let $M= M_1 \#M_2$ , where each $M_i$ is a thickened annulus ${\mathbb A} \times [-1,1]$ , a solid torus. Let $x_i$ be the core of $M_i$ . Recall that $\Psi _{M_1,M_2;\epsilon }$ is the connected sum homomorphism (Subsection 3.2). Define

$$ \begin{align*}x= \Psi_{M_1,M_2;\epsilon }((x_1^2-4) \otimes (x_2^2-4)) \in {\mathscr S}_\epsilon(M) .\end{align*} $$

By definition,

$$ \begin{align*}\Phi_{q^{1/2}}(x)= \Psi_{M_1,M_2;q^{1/2}} ( (T_N(x_1)^2-4) \otimes (T_N(x_2)^2-4)) \in {\mathscr S}_{q^{1/2}}(M) .\end{align*} $$

Let us show that $T_n(x)^2-4 \in S_{n-1}(x) \mathbb Z[x]$ . Embed $\mathbb Z[x] \hookrightarrow \mathbb Z[u^{\pm 1}]$ by $x=u+ u^{-1}$ . Then

$$ \begin{align*} T_n(x)^2-4 = (u^n + u^{-n})^2-4=(u^n - u^{-n})^2 = (u-u^{-1})^2 S_{n-1}(x)^2 \in S_{n-1} (x) \mathbb Z[x]. \end{align*} $$

Thus, $(T_N(x_1)^2-4) \otimes (T_N(x_2)^2-4)\in F_{q^{1/2}}(M_1) \otimes F_{q^{1/2}}(M_2)$ . By Corollary 3.6, we have $\Phi _{q^{1/2}}(x)=0$ .

It remains to show $x\neq 0$ in ${\mathscr S}_\epsilon (M)$ .

First, we assume $\epsilon ^2= \pm 1$ . In this case, ${\mathscr S}_\epsilon (M)$ has the structure of a commutative algebra where for two disjoint framed links $\alpha $ and $\beta $ in M the product $\alpha \beta $ is the disjoint union $\alpha \sqcup \beta $ . As a ${\mathbb C}$ -algebra, ${\mathscr S}_\epsilon (M)$ is isomorphic to the universal $SL_2$ -character variety of M; see [Reference Bullock7, Reference Przytycki and Sikora33]. In particular, there is a surjective algebra homomorphism $\Omega : {\mathscr S}_\epsilon (M) \to {\mathbb C}[\chi (M)]$ , where $\chi (M)$ is the $SL_2({\mathbb C})$ -character variety of the fundamental group $\pi _1(M)$ . The fundamental group of M is free on two generators $z_1$ and $z_2$ , where $z_i$ is a loop representing the core of $M_i$ . It is known that ${\mathbb C}[\chi (M)]$ is the ring of polynomials in three variables $u_1=\operatorname {\mathrm {tr}}(z_1), u_2=\operatorname {\mathrm {tr}}(z_2)$ and $u_{12}=\operatorname {\mathrm {tr}}(z_1z_2)$ . In particular, we have an embedding ${\mathbb C}[u_1, u_2 ] \hookrightarrow {\mathbb C}[\chi (F_2)]$ . By definition, $\Omega (x_1)= \mathsf {Sign}(x_i) u_i$ , where $\mathsf {Sign}(x_i) \in \{\pm 1\}$ whose exact value is not important as $\Omega (x_1^2)= u_i^2$ . It follows that

$$ \begin{align*}\Omega(x) = (u_1^2-4)(u_2^2-4) \neq 0 \ \text{in } {\mathbb C}[u_1, u_2 ] \subset {\mathbb C}[\chi(F_2)].\end{align*} $$

Hence, $x\neq 0$ .

Now, assume $\epsilon ^2=\pm i$ . Note that M can be embedded into $S^3$ since each solid torus $M_i$ can. Sikora [Reference Sikora35] showed that when M can be embedded into a homology sphere, the skein module ${\mathscr S}_\epsilon (M)$ , with $\epsilon ^2=\pm i$ , has a commutative algebra structure such that if $\alpha , \beta $ are framed knots them $\alpha \beta = s(\alpha ,\beta ) (\alpha \cup \beta )$ , where $s(\alpha ,\beta )\in \{ \pm 1\}$ . Moreover, the algebra ${\mathscr S}_\epsilon (M)$ is also isomorphic to the universal $SL_2({\mathbb C})$ -character ring of M, and we get a surjective algebra homomorphism $\Omega : {\mathscr S}_\epsilon (M) \to {\mathbb C}[\chi (M)]$ . Now, $\Omega (x_i) = \pm q^{d_i} u_i$ , where $d_i\in \mathbb Z$ . It follows that

$$ \begin{align*}\Omega(x) = (\pm q^{2d_1} u_1^2-4)(\pm q^{2d_2} u_2^2-4) \neq 0 \ \text{in } {\mathbb C}[u_1, u_2 ] \subset {\mathbb C}[\chi(F_2)].\end{align*} $$

Hence, $x\neq 0$ . This completes the proof of the theorem.

3.7 Proofs

For integers $k,m \ge 0$ , let $v_{k,m}$ and $u_{k,m}$ be the elements defined in Figure 5, which are patterns, that is, elements of $\mathsf {TL}_{2(k+m)}$ . Here, each box stands for the Jones–Wenzl idempotent $f_{k+m}$ . A circle enclosing a number k means there are k parallel strands passing the circle. By convention, $u_{0,0}= v_{0,0} =\emptyset $ .

Figure 5 The elements $v_{k,m}$ and $u_{k,m}$ .

The proof of the following main technical lemma uses only the nonreturnable property of the Jones–Wenzl idempotent.

Lemma 3.12. If $k\ge 1$ , then

(20) $$ \begin{align} u_{k,m} = q^{4k-2} v_{k,m} + q^{2k-4}(q^{2k } -q^{-2k} ) v_{k-1, m+1}. \end{align} $$

Proof. The skein relation (1) replaces a crossing with the sum of a positive and a negative resolution of the crossing, each with a positive or negative power of q. The nonreturning property of the Jones–Wenzl idempotent (16) shows that for the upper $2k-2$ crossings in $k_{k,m}$ only the positive resolution results in a nonzero term. Hence,

(21)

Resolve the upper left crossing,

For the first tangle, resolve the crossings on the left from top to bottom, then the crossings on the right from bottom to top, except for the very last one. Only positive resolutions contribute. For the second tangle, resolve the left crossings from top to bottom. Only negative resolutions contribute. Thus, we have

For the left tangle, resolve the crossing in two ways. For the right one, note that removing the kink using Equation (5). After that, only negative resolutions contribute. Eventually, we get

Using the above identity in Equation (21), we get Equation (20).

Proof. Proof (Proof of Theorem 3.1).

Assume that the shaded rectangle D in the picture of $v_{k,m}$ (Figure 5) is embedded in $M= M_1 \#M_2$ so that the separating sphere S of the connected sum $M_1 \#M_2$ meets D in the vertical line separating D into two equal halves. In what follows, $x \overset {\#}{=} x'$ for $x,x'\in \mathsf {TL}_{2k+2m}$ means that if $\mathsf {cl}(x)$ and $\mathsf {cl}(x')$ are closures of x and $x'$ , respectively, by the same closing element not meeting $S $ , then $\mathsf {cl}(x)=\mathsf {cl}(x')$ as elements of ${\mathscr S}_{q^{1/2}}(M)$ .

Sliding the top strand of $v_{k, m}$ over the sphere $S^2$ and taking into account the framing, we get

$$ \begin{align*}u_{k,m} \overset{\#}{=} q^{-6} v_{k,m}, \quad \text{if} \ k\ge 1.\end{align*} $$

Using Equation (20), we get

$$ \begin{align*}q^{-6} v_{k,m} \overset{\#}{=} q^{4k-2} v_{k,m} + q^{2k-4}(q^{2k } -q^{-2k} ) v_{k-1, m+1}\end{align*} $$

Multiply by $q^{4-2k}$ ,

$$ \begin{align*}(q^{-2k-2 } -q^{2k+2} ) v _{k,m} \overset{\#}{=} (q^{2k } -q^{-2k} ) v _{k-1,m+1}.\end{align*} $$

Replacing k by $k-1$ and continue until $k=1$ , we get

(22) $$ \begin{align} (q^{-2k-2 } -q^{2k+2} ) v _{k,m} \overset{\#}{=} (-1)^k(q^{2 } -q^{-2} ) v _{0,m+k}. \end{align} $$

Let $m=0$ and $k=N-1$ . The scalar of the left-hand side is 0 because $\mathrm {ord}(q^4)= N$ , and the scalar of the right side is not 0. Hence, $ v_{0, N-1} \overset {\#}{=} 0.$

Since any element of $F_{q^{1/2}}(M_1) \otimes F_{q^{1/2}}(M_2)$ is a linear combination of closures of $v_{0,N-1}$ , we have $F_{q^{1/2}}(M_1) \otimes F_{q^{1/2}}(M_2)\overset {\#}{=} 0$ . This completes the proof of Theorem 3.1.

Proof of Theorem 3.8.

By definition there are components $e_1, e_2$ of $ \mathcal N$ and a properly embedded path a in M meeting S transversally at one point such that one endpoint of a is in $e_1$ and the other is in $e_2$ . It might happen that $e_1=e_2$ . Let $\alpha $ be a stated $\mathcal N$ -link contained in $M\setminus S$ . We can embed the shaded square D into $M\setminus \alpha $ so that the left side of D is $e_1$ , the right side is $e_2$ and S meets D in the vertical line dividing D into two equal halves.

For integers $k,m \ge 0$ , let $v^{\prime }_{k,m}$ and $u^{\prime }_{k,m}$ be the stated diagrams on D as given in Figure 6.

Figure 6 The elements $v'_{k,m}$ and $u'_{k,m}$ .

Here, on a left side or right side, from bottom to top, there are $k+m$ negative states followed by $k+m$ positive states. Note the similarity between $v^{\prime }_{k,m}$ and $v_{k,m}$ , and $u^{\prime }_{k,m}$ and $u_{k,m}$ . Instead of the Jones–Wenzl boxes at the boundary in $v_{k,m}$ and $u_{k,m}$ , we have states, all positive or all negative in a place where we had a box before. Because they are the same states, we still have the nonreturnable property by the defining relation (3) of stated skein modules. Since $\alpha $ is contained outside a neighborhood of $S\cup D$ , the proof of Lemma 3.12 and subsequent arguments, where we used only the nonreturnable property of the Jones–Wenzl idempotent, are still valid if we replace $v_{k,m}$ and $u_{k,m}$ by $v^{\prime }_{k,m}\sqcup \alpha $ and $u^{\prime }_{k,m}\sqcup \alpha $ . Thus, we have the analog of Identity (22)

$$ \begin{align*} (q^{-2k-2 } -q^{2k+2} ) (v' _{k,m}\sqcup \alpha) = (-1)^k(q^{2 } -q^{-2} ) ( v' _{0,m+k} \sqcup \alpha). \end{align*} $$

Again, let $m+k=N-1$ . Then the left-hand side is 0. Hence, $v' _{0,N-1}\sqcup \alpha =0$ . But $v' _{0,N-1}$ consists of $2(N-1)$ trivial arcs, each has one positive and one negative state. From the defining relation (3), we have

$$ \begin{align*}v' _{0,N-1}\sqcup \alpha = q^{l/2} \alpha, \ l \in \mathbb Z.\end{align*} $$

It follows that $\alpha =0$ in ${\mathscr S}_{q^{1/2}}(M,\mathcal N)$ .

Proof of Theorem 3.9.

Let M be the result of removing the 3-ball $d \times c$ from $S^2 \times S^1$ , where $d\subset S^2$ is an open disk and $c\subset S^1$ is an open interval. The embedding $Y \hookrightarrow S^2 \times S^1$ induces an isomorphism of skein modules. The skein module ${\mathscr S}(S^2 \times S^1; {\mathbb Z[q^{\pm 1/2}]})$ over the ring ${\mathbb Z[q^{\pm 1/2}]}$ has been calculated by Hoste and Przytycki [Reference Hoste and Przytycki18]:

(23) $$ \begin{align} {\mathscr S}(S^2 \times S^1; {\mathbb Z[q^{\pm 1/2}]}) = {\mathbb Z[q^{\pm 1/2}]} \oplus \bigoplus_{i=1}^\infty {\mathbb Z[q^{\pm 1/2}]}/(1-q^{2i+4}), \end{align} $$

where the first component ${\mathbb Z[q^{\pm 1/2}]}$ is the free ${\mathbb Z[q^{\pm 1/2}]}$ -module generated by $\emptyset $ . By change of ground ring, we have $\emptyset \neq 0$ in ${\mathscr S}_{q^{1/2}}(Y)$ , for any nonzero $q^{1/2}\in {\mathbb C}$ .

Let E be the disk $E=d'\times \{t\}$ , where $d'= S^2 \setminus d$ and $t\in c$ , and e be an open interval in E. Let $(M', \mathcal N')$ be the result of cutting Y along $(E,e)$ , with $\mathcal N'= e_1 \cup e_2$ , where each $e_i$ is a preimage of e. The two components $e_1$ and $e_2$ are separated by the sphere $S^2 \times t'$ , where $t'\not \in c$ . By Theorem 3.8, we have $\emptyset =0$ in ${\mathscr S}_{q^{1/2}}(M', \mathcal N')$ , but $\emptyset $ is not 0 in ${\mathscr S}_{q^{1/2}}(Y)$ . This shows the cutting homomorphism is not injective.

4.1 Marked surfaces

Such an embedding induces an embedding of the corresponding thickened surfaces, and hence an R-linear map $j_*: {\mathscr S}(\Sigma , \mathcal P) \to {\mathscr S}(\Sigma ', \mathcal P').$

Suppose $\mathcal P$ has no circular component. The skein module ${\mathscr S}(\Sigma , \mathcal P)$ has an algebra structure where the product of two stated $\mathcal N$ -tangles $\alpha $ and $\beta $ is obtained by stacking $\alpha $ above $\beta $ . This means, we first isotope so that $\alpha \subset \Sigma \times (0,1)$ and $\beta \subset (-1,0)$ then define $\alpha \beta = \alpha \cup \beta $ . For $e=p\times (-1,1)$ where $p\in \mathcal P^0$ , we will denote ${\mathsf {inv}}_p={\mathsf {inv}}_e$ , where ${\mathsf {inv}}_e$ defined in Proposition 2.6. Remark that with this product, the map ${\mathsf {inv}}_p$ is an algebra isomorphism.

For a marked surface $(\Sigma ,\mathcal P)$ , its associated boundary-oriented surface $\mathfrak S= \mathfrak S_{(\Sigma ,\mathcal P) }$ is defined as follows. For each $p\in \mathcal P^0$ , let $N(p)\subset { \partial \Sigma }$ be a small open interval containing p. Let $\mathfrak S$ be the result of removing the boundary ${ \partial \Sigma }$ , except for $\mathcal P^1$ and all the $N(p)$ , from  $\Sigma $ :

$$ \begin{align*}\mathfrak S= (\Sigma\setminus { \partial \Sigma} ) \cup \mathcal P^1 \cup (\bigcup_{p\in \mathcal P^0} N(p)) .\end{align*} $$

The orientation ${ \mathsf {or}}$ on $\partial \mathfrak S= (\bigcup _{p\in \mathcal P^0} N(p)) \cup \mathcal P^1$ is defined by: A component in $\mathcal P^1$ is already oriented, while a component $N(p)$ is oriented by the orientation coming from $\mathfrak S$ or its reverse according as p is positive or negative. The resulting $(\mathfrak S,{ \mathsf {or}})$ is a boundary-oriented surface.

The requirement that each connected component of $\Sigma $ has at least one marked points implies that each connected component of $\mathfrak S$ has a boundary edge. Conversely, it is easy to see that every boundary-oriented surface $\mathfrak S$ , where each connected component has at least one boundary edge is of the form $\mathfrak S= \mathfrak S_{(\Sigma , \mathcal P)}$ for certain marked surface $(\Sigma , \mathcal P)$ .

Identify ${\mathscr S}(\Sigma , \mathcal P)$ with ${\mathscr S}(\mathfrak S)$ via the following R-linear isomorphism

$$ \begin{align*}{\mathscr S}(M, \mathcal N) \xrightarrow{{\mathsf{inv}} } {\mathscr S}(M, \mathcal N') \xrightarrow{f_* } {\mathscr S}(M, \mathcal P^1 \cup (\cup_{p} N(p) ),\end{align*} $$

where

• • ${\mathsf {inv}}$ is the composition of ${\mathsf {inv}}_p$ of all negative $p\in \mathcal P^0$ , and $\mathcal N'$ is the same as $\mathcal N$ , except that the orientation of each $p \times (-1,1)$ is the one coming from $(-1,1)$ ,

• • $f: (M,\mathcal N') \to (M, \mathcal P^1 \cup (\cup _{p} N(p) )$ is identity except in a small neighbourhood of each $N(p) \times (-1,1)$ in which it rotates $p\times (-1,1)$ by $\pi /4$ or $-\pi /4$ to make it become $N(p)$ , matching the natural orientation of $p\times (-1,1)$ with the orientation ${ \mathsf {or}}$ of $N(p)$ .

We will often use the above identification ${\mathscr S}(\Sigma , \mathcal P)\equiv {\mathscr S}(\mathfrak S).$ With this identification, the skein module ${\mathscr S}(\mathfrak S,{ \mathsf {or}})$ of a circle free boundary-oriented surface has an algebra structure which was studied in many works, for example, [Reference Lê26, Reference Costantino and Le10, Reference Lê and Yu29, Reference Lê and Yu30, Reference Korinman and Quesney22].

4.2 The bigon

From now on, let ${\mathbb P}_2$ be the boundary-oriented bigon where the boundary orientation is positive on one edge, called the right edge $e_r$ , and negative on the other, called the left edge $e_l$ ; see Figure 7(a). The corresponding marked surface is ${\mathbf P}_2= (D, \mathcal P)$ , where D is the standard closed disk and $\mathcal P$ consists of two points in $\partial D$ , one positive and one negative.

Figure 7 (a) Bigon ${\mathbb P}_2$ . (b) The horizontal arc. (c) Product $xy$ .

Let $a,b,c,d$ be the stated $\partial {\mathbb P}_2$ -arc of Figure 7(b), where $\nu \mu $ are, respectively, $++, +-, -+, --$ . In [Reference Lê26, Reference Costantino and Le10], it is proved that the algebra ${\mathscr S}({\mathbb P}_2)$ is generated by $a,b,c,d$ subject to the following relations:

$$ \begin{align*} ba&= q^2 ab, ca = q^2 ac, db = q^2 bd, dc = q^2 cd \\ bc &= cb, ad - q^{-2} bc = da - q^{2} bc =1. \end{align*} $$

The product of two elements, represented by stated $\partial {\mathbb P}_2$ -tangle diagrams x and y, is the union $x\cup y$ where we first isotope x so that it is higher than y; see Figure 7(c).

In [Reference Costantino and Le10], we defined geometrically the coproduct, counit and antipode which make ${\mathscr S}({\mathbb P}_2)$ a Hopf algebra. The coproduct is particularly simple: By cutting the bigon ${\mathbb P}_2$ along the ideal arc connecting the two vertices, we get two copies of ${\mathbb P}_2$ , and the cutting homomorphism is the coproduct $\Delta $ . On the generators, the counit $\varepsilon $ and the antipode S are given by

(24) $$ \begin{align} \varepsilon(a) &= \varepsilon(d)=1, \varepsilon(b)= \varepsilon(c)=1 \end{align} $$

(25) $$ \begin{align} S(a) &= d, S(d)=a, S(b) = - q^2 b, S(c) = - q^{-2} c. \end{align} $$

The above Hopf algebra is the well-known quantised coordinate algebra ${\mathcal O}_{q^2}(\mathrm {SL}(2))$ of the Lie group $SL(2)$ . The following was proved in [Reference Costantino and Le10]:

4.3 The annulus

Let ${\mathbb A}= [-1,1] \times S^1$ be the boundary-oriented annulus with one positive orientation on one boundary component, called the right component, and one negative orientation on the other, called the left component. A slit along a properly embedded arc connecting the two boundary components yields the bigon ${\mathbb P}_2$ , where the right (resp. left) component goes to the right (resp. left) edge. By Theorem 2.13,

$$ \begin{align*}{\mathscr S}({\mathbb A}) = {\mathscr S}({\mathbb P}_2)/\sim = {\mathcal O}_{q^2}(\mathrm{SL}(2))/\sim\!.\end{align*} $$

Relation $\sim $ of Theorem 2.13, with the product structure as described in Subsection 4.1, translates to $xy = yx$ for all $x,y\in {\mathcal O}_{q^2}(\mathrm {SL}(2))$ . Thus, we have

$$ \begin{align*}{\mathscr S}({\mathbb A}) = {\mathcal O}_{q^2}(\mathrm{SL}(2))/(xy-yx),\end{align*} $$

which is known as the 0-th Hochchild homology $\mathrm {HH_0}({\mathcal O}_{q^2}(\mathrm {SL}(2)))$ . This space was computed in [Reference Feng and Tsygan14] over $\mathbb {C}$ when q is not a root of unity; its complete structure when working over arbitrary ground ring ${R}$ is unknown to us. But it is not difficult to show that over the ring ${\mathbb Z[q^{\pm 1/2}]}$ the module $\mathrm {HH_0}({\mathcal O}_{q^2}(\mathrm {SL}(2)))$ contains torsion. For instance, it is an easy exercise to show that $(q^2-1)\tau (ab)=0$ but $\tau (ab)\neq 0$ , where $\tau : {\mathcal O}_{q^2}(\mathrm {SL}(2)) \twoheadrightarrow \mathrm {HH_0}({\mathcal O}_{q^2}(\mathrm {SL}(2)))$ is the natural projection and $a,b$ are the generators given in Subsection 4.2. We also observe for later purposes that if $\gamma $ is the core of the annulus, then by Lemma 2.15 we have $\gamma =2[\emptyset ]$ in $\mathrm {HH_0}({\mathcal O}_{q^2}(\mathrm {SL}(2)))$ .

Note that the product in ${\mathcal O}_{q^2}(\mathrm {SL}(2))$ does not descend to a product in $\mathrm {HH_0}({\mathcal O}_{q^2}(\mathrm {SL}(2)))$ . However, the coalgebra structure does descend to $\mathrm {HH_0}({\mathcal O}_{q^2}(\mathrm {SL}(2)))$ . For this, we need to check that $\sim $ is a coideal. In fact, if $\Delta (x)=x_{1}\otimes x_2$ and $\Delta (y)=y_{1}\otimes y_2$ (in Sweedler’s notation), then

$$ \begin{align*}\Delta([x,y])=[x_1,y_1]\otimes x_2y_2+y_1x_1\otimes [x_2,y_2]\end{align*} $$

and $\epsilon ([x,y])=0$ . Here $[x,y]= xy-yx$ .

As in [Reference Costantino and Le10], the existence of the cutting morphism allows to prove the following:

4.4 Comodule structure of ${\mathscr S}(M,\mathcal N)$

Let $(M,\mathcal N)$ be a marked manifold and c be a component of $\mathcal N$ . We will show that associated to c is a comodule structure of ${\mathscr S}(M,\mathcal N)$ over ${\mathscr S}(\mathcal P_2)$ (if c is an arc) or $\mathrm {HH}_0({\mathcal O}_{q^2}(\mathrm {SL}(2)))$ (if c is a circle).

Suppose first that c is an oriented arc, that is, c is the image of $(-1,1)$ via a smooth embedding of $[-1,1]$ in $\partial M$ . Let us denote $\overline {c}$ the image of $[-1,1]$ via the embedding. Let $N(c)$ be a regular neighbourhood of $\overline {c}$ in M, and ${\mathsf {interior}}(N(c))$ be the interior of $N(c)$ .

Let $D^2$ be the unit disc in $\mathbb {C}$ , and let $\psi _+:N(c) \to D^2\times I$ (resp. $\psi _-$ ) be an orientation preserving diffeomorphism sending c to $\{+1\}\times (-1,1)$ (resp. $\{-1\}\times (-1,1)$ ). Letting $M'=M\setminus {\mathsf {interior}}(N(c))$ , there exists an orientation preserving diffeomorphism $\phi :M'\to M$ unique up to isotopy which is the identity out of a neighbourhood of $N(c)$ ; let $\mathcal N'=\phi ^{-1}(\mathcal N)$ and $c'=\phi ^{-1}(c)$ . Endow $N(c)$ with the marking $\mathcal N"=\{\pm 1\}\times (-1,1)$ . Cutting $N(c)$ out of M is obtained by cutting along a properly embedded disc D containing $c'$ and by Theorem 2.18 we obtain a morphism:

$$ \begin{align*}\mathsf{Cut}_{D,c'}:{\mathscr S}(M,\mathcal N)\to {\mathscr S}(M',\mathcal N')\otimes_{R}{\mathscr S}(N(c),\mathcal N")={\mathscr S}(M,\mathcal N)\otimes_{R} {\mathscr S}(N(c),\mathcal N"),\end{align*} $$

where the second equality is induced by $\phi _*\otimes Id_{{\mathscr S}(N(c),\mathcal N")}.$ Now, observe that $(N(c),\mathcal N")$ is diffeomorphic to a thickened bigon endowed with two positive markings. In order to get the bigon with a negative and a positive marking (whose stated skein algebra, as recalled in Subsection 4.2, is canonically ${\mathcal O}_{q^2}(\mathrm {SL}(2))$ ) we need to apply one inversion morphism ${\mathsf {inv}}$ . Via the identification $\psi _+$ (resp. $\psi _-$ ) the image of c is $e_r=\{1\}\times (-1,1)$ (resp. $e_l=\{-1\}\times (-1,1)$ ). Therefore, in order to get a right ${\mathcal O}_{q^2}(\mathrm {SL}(2))$ -module structure on ${\mathscr S}(M,\mathcal N)$ we define:

$$ \begin{align*}\Delta_R=(Id_{{\mathscr S}(M,\mathcal N)}\otimes ({\mathsf{inv}}_{e_l}\circ (\psi_+)_*))\circ \mathsf{Cut}_{D,c'}\qquad\end{align*} $$

and in order to get a left ${\mathcal O}_{q^2}(\mathrm {SL}(2))$ -module structure we define:

$$ \begin{align*}\Delta_L=(({\mathsf{inv}}_{e_l}\circ (\psi_-)_*)\otimes \mathrm{Id}_{{\mathscr S}(M,\mathcal N)}) \circ \tau\circ \mathsf{Cut}_{D,c'}\end{align*} $$

where $\tau (x\otimes y)=y\otimes x$ .

Proposition 4.5.

$$ \begin{align*}\Delta_R:{\mathscr S}(M,\mathcal N)\to {\mathscr S}(M,\mathcal N)\otimes {\mathscr S}(D^2\times I,\{1\}\times [-1,1])\end{align*} $$

is a right comodule structure. Similarly,

$$ \begin{align*}\Delta_L:{\mathscr S}(M,\mathcal N)\to {\mathscr S}(D^2\times I,\{-1\}\times [-1,1])\otimes {\mathscr S}(M,\mathcal N)\end{align*} $$

is a left comodule structure.

Proof. The proof is similar to the proof of coassociativity of the coaction for the case of boundary oriented surfaces given in [Reference Costantino and Le10]. If $D'\subset M$ is another properly embedded disc parallel to D and we let $c"\subset D'$ be an oriented edge parallel to $c'$ , then by the commutativity statement of Theorem 2.18, we get the associativity of the coaction:

$$ \begin{align*}{\mathsf{inv}}_{d"}\circ {\mathsf{inv}}_{d'}\circ \mathsf{Cut}_{D',c"}\circ \mathsf{Cut}_{D,c'}={\mathsf{inv}}_{d"}\circ {\mathsf{inv}}_{d'}\circ \mathsf{Cut}_{D,c'}\circ \mathsf{Cut}_{D',c"},\end{align*} $$

where we let $d'$ (resp. $d"$ ) be the copy of $c'$ (resp. $c"$ ) contained in the component of $\mathsf {Cut}_{D,c'}$ (resp $\mathsf {Cut}_{D',c"}$ ) containing c.

If instead c is a circle marking, let $N(c)$ be a regular neighbourhood of c in M, diffeomorphic to the thickening of the annulus ${\mathbb A}$ (see Subsection 4.3) via an orientation preserving diffeomorphism $\psi _+$ (resp. $\psi _-$ ) such that $\psi _+(c)$ is the positive (resp. negative) boundary component of ${\mathbb A}$ . Let $\mathcal N"$ be a marking on $N(c)$ given by $\psi _+^{-1}(\partial {\mathbb A}\times \{0\})$ (resp. $\psi _-^{-1}(\partial {\mathbb A}\times \{0\})$ ).

As above, there exists a diffeomorphism $\phi :M'=M\setminus {\mathsf {interior}}(N(c))\to M$ which is the identity out of a regular neighbourhood of $N(c)$ , unique up to isotopy. Letting $\mathcal N'=\phi ^{-1}(\mathcal N)$ and $c'=\phi ^{-1}(c)$ , we can then identify ${\mathscr S}(M',\mathcal N')$ and ${\mathscr S}(M,\mathcal N)$ via $\phi _*$ . Let then $D\subset M$ be a properly embedded annulus containing $c'$ ; applying Theorem 2.18, we then define

$$ \begin{align*}\mathsf{Cut}_{D,c'}:{\mathscr S}(M,\mathcal N)\to {\mathscr S}(M',\mathcal N')\otimes_{R}{\mathscr S}(N(c),\mathcal N")={\mathscr S}(M,\mathcal N)\otimes_{R} {\mathscr S}(N(c),\mathcal N"),\end{align*} $$

where the second equality is induced by $\phi _*\otimes Id_{{\mathscr S}(N(c),\mathcal N")}$ . By Proposition 4.4, we have ${\mathscr S}(N(c), \mathcal N")=\mathrm {HH}_0({\mathcal O}_{q^2}(\mathrm {SL}(2)))$ . Therefore, we get a right $\mathrm {HH}_0({\mathcal O}_{q^2}(\mathrm {SL}(2)))$ -comodule structure on ${\mathscr S}(M,\mathcal N)$ via:

$$ \begin{align*}\Delta_R=(\mathrm{Id}_{{\mathscr S}(M,\mathcal N)}\otimes (\psi_+)_*) \circ \Delta\end{align*} $$

or a left $\mathrm {HH}_0({\mathcal O}_{q^2}(\mathrm {SL}(2)))$ -comodule structure via:

$$ \begin{align*}\Delta_L=((\psi_-)_*\otimes \mathrm{Id}_{{\mathscr S}(M,\mathcal N)} ) \circ \tau \circ \Delta,\end{align*} $$

where $\tau (x\otimes y)=y\otimes x$ .

Proposition 4.6.

$$ \begin{align*}\Delta_R:{\mathscr S}(M,\mathcal N)\to {\mathscr S}(M,\mathcal N)\otimes {\mathscr S}({\mathbb A}\times [-1,1],\partial {\mathbb A}\times \{0\})\end{align*} $$

is a right comodule structure. Similarly,

$$ \begin{align*}\Delta_L:{\mathscr S}(M,\mathcal N)\to {\mathscr S}({\mathbb A}\times [-1,1],\partial {\mathbb A}\times \{0\})\otimes {\mathscr S}(M,\mathcal N)\end{align*} $$

is a left comodule structure.

Proof. If $D'\subset M$ is another properly embedded annulus parallel to D and we let $c"\subset D'$ be its core oriented as $c'$ , then by the commutativity statement of Theorem 2.18, we get

$$ \begin{align*}\mathsf{Cut}_{D',c"}\circ \mathsf{Cut}_{D,c'}=\mathsf{Cut}_{D,c'}\circ \mathsf{Cut}_{D',c"}\end{align*} $$

which proves coassociativity.

4.5 Module structure of ${\mathscr S}(M,\mathcal N)$

Let $(\Sigma ,\mathcal P)$ be a marked surface, and let $\phi :{\Sigma }\to \partial M$ be an embedding; we will say that the sign of $\phi $ is $+1$ if $\phi $ is orientation preserving and $-1$ otherwise. Recall that by hypothesis each edge of $\mathcal N$ is the image of $(-1,1)$ through an embedding of $[-1,1]$ in $\partial M$ ; therefore, we will talk of ‘target’ of the edge c (the image of $\{1\}$ ) and of its source (the image of $\{-1\}$ ) and we will denote $\overline {c}$ and $\overline {\mathcal N}$ the closures, respectively, of c and of $\mathcal N$ in $\partial M$ .

Suppose that $\overline {\mathcal N}\subset \partial M$ is such that $\overline {\mathcal N}\cap \phi (\Sigma )=\phi (\mathcal P)$ and that for each $p\in \mathcal P$ , if $c\in \mathcal N$ is the component such that $\overline {c}\cap \phi (\Sigma )=\{p\}$ , then p is the target of c if $\mathsf {Sign}(p)\mathsf {Sign}(\phi )=1$ and it is the source of c if $\mathsf {Sign}(p)\mathsf {Sign}(\phi )=-1$ (here, $\mathsf {Sign}(p)$ is the sign of the component of $\mathfrak S$ containing it).

Then a regular neighbourhood of $\phi (\Sigma )$ in M is diffeomorphic to $(\Sigma \times [-1,1],\mathcal P\times [-1,1])$ : Let $i:(\Sigma \times [-1,1],\mathcal P\times [-1,1])\to (M,\mathcal N)$ the embedding. Furthermore, there is a diffeomorphism $\psi :M\to M\setminus {\mathsf {interior}}(i(\Sigma \times [-1,1]))$ isotopic to the identity of M.

We can define a left action (resp. a right action) of $\alpha \in {\mathscr S}(\Sigma ,\mathcal P)$ on $m\in {\mathscr S}(M,\mathcal N)$ as

$$ \begin{align*}\alpha\cdot m:=[i(\alpha) \sqcup \psi(m)]\ (\mathrm{{respectively}} \ m\cdot \alpha:=[\psi(m)\sqcup i(\alpha)]),\end{align*} $$

where $[x]$ denotes the class in ${\mathscr S}(M,\mathcal N)$ of the stated tangle x. The proof of the following proposition is straightforward and left to the reader:

Furthermore, recall that for each edge $p\in \mathcal P$ the algebra ${\mathscr S}(\Sigma ,\mathcal P)$ is also a ${\mathcal O}_{q^2}(\mathrm {SL}(2))$ -comodule algebra; it is not difficult to prove that the above result actually holds in the category of ${\mathcal O}_{q^2}(\mathrm {SL}(2))$ -comodules, namely that for each $e\in \mathcal N$ if ${\mathscr S}(M,\mathcal N)$ and ${\mathscr S}(\Sigma ,\mathcal P)$ are endowed with the right ${\mathcal O}_{q^2}(\mathrm {SL}(2))$ -comodule structure associated to e (resp. $e\cap \Sigma $ ), then it holds:

$$ \begin{align*}\Delta_e(\alpha\cdot m)=\Delta_e(\alpha)\cdot \Delta_e(m)\ \mathrm{(resp.}\ \Delta_e(m\cdot \alpha)=\Delta_e(m)\cdot \Delta_e(\alpha) ),\end{align*} $$

where in the right-hand side of the equalities $\cdot $ stands for the tensor product of the action and of the product in ${\mathcal O}_{q^2}(\mathrm {SL}(2))$ .

4.6 Sphere lemma

Suppose that one component of $\partial M$ is a sphere endowed with a single oriented arc $e\in \mathcal N$ , and let ${\mathscr S}_0(M,\mathcal N)$ be the sub ${R}$ -module generated by stated skeins represented by arcs not intersecting e. Let also $\hat {M}$ be obtained by filling M with a ball $B^3$ along that boundary component and $\hat {\mathcal N}=\mathcal N\setminus e\subset \partial \hat {M}$ . Let ${{R}}^{loc}$ be the ring obtained by localising ${R}$ by the multiplicative set generated by $\mathbb {Z}\setminus \{0\}\cup \{1-q^{2n+4},n\geq 1\}$ .

Proposition 4.10. (Sphere lemma)

$$ \begin{align*}{R}^{loc}\otimes {\mathscr S}(M,\mathcal N)={R}^{loc}\otimes {\mathscr S}_0(M,\mathcal N)={R}^{loc}\otimes {\mathscr S}(\hat{M},\hat{\mathcal N}).\end{align*} $$

Proof. The second equality is clear as isotopy in $\hat {M}$ is the same as isotopy in M for arcs not touching $\partial B^3$ , and we note here that it holds over ${R}$ . To prove the first equality, we apply the standard sphere trick: If $\alpha $ is a stated skein such that $\alpha \cap \partial B^3$ has n points, then we can isotope one strand of $\alpha $ around $\partial B^3$ so to get the equality of Figure 8. Then applying relations (1) to all the crossings and then Equation (3), we have the following equality: $\alpha =+q^{6}\cdot q^{2(n-1)} \alpha + l.o.t.$ , where $l.o.t$ stands for a linear combination of skeins whose intersection with $\partial B^3$ has less than n points. As a consequence since $1-q^{2n+4}$ is invertible in ${R}^{loc}$ we can express $\alpha $ a linear combination of skeins with lower intersection with B. Arguing by induction on this number of intersections, we prove that each skein can be represented as a linear combination of skeins not intersecting B.

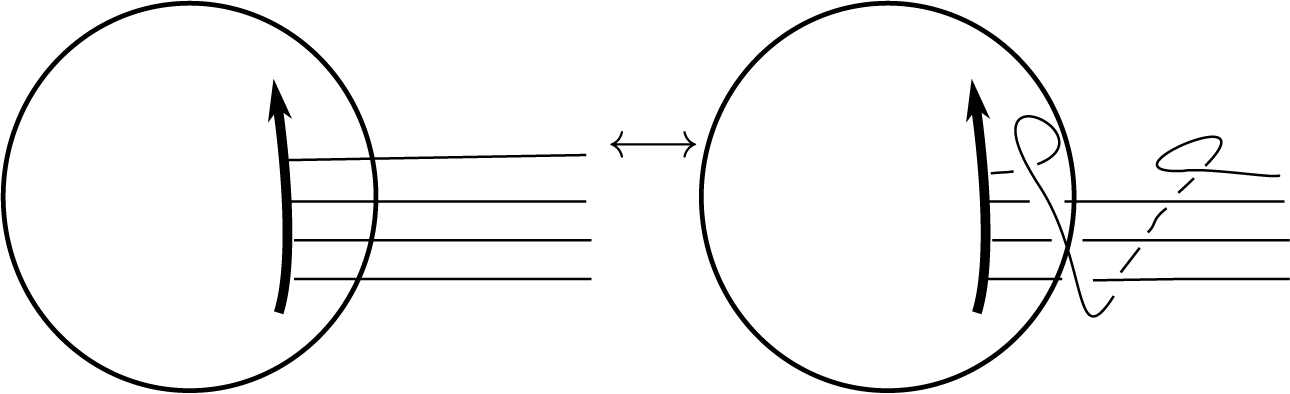
Figure 8 Isotopy of one strand around the sphere in the case $n=4$ .