1. Introduction
Let
![]() $(M,d,\mu )$
be a metric measure space. The central theme of our contribution is the question whether a semigroup of compact operators
$(M,d,\mu )$
be a metric measure space. The central theme of our contribution is the question whether a semigroup of compact operators
![]() $\left \{U_t: t \geqslant 0 \right \}$
acting on the scale of Lebesgue spaces
$\left \{U_t: t \geqslant 0 \right \}$
acting on the scale of Lebesgue spaces
![]() $L^p(\mu ) = L^p(M,\mu )$
admits some ‘ergodic’ measure. More precisely, we look at expressions of the from
$L^p(\mu ) = L^p(M,\mu )$
admits some ‘ergodic’ measure. More precisely, we look at expressions of the from

and we establish conditions on
![]() $\left \{U_t: t \geqslant 0 \right \}$
such that the limit in (1.1) i) exists, ii) exists uniformly for certain families of measures
$\left \{U_t: t \geqslant 0 \right \}$
such that the limit in (1.1) i) exists, ii) exists uniformly for certain families of measures
![]() $\sigma $
and functions f, iii) converges with a certain rate (in time and space), and iv) that m is the unique quasi-stationary measure. In many situations, the rate can be explicitly given, and it is even exponential in time t. The measure m, which is sometimes called a quasi-ergodic, has a very concrete form
$\sigma $
and functions f, iii) converges with a certain rate (in time and space), and iv) that m is the unique quasi-stationary measure. In many situations, the rate can be explicitly given, and it is even exponential in time t. The measure m, which is sometimes called a quasi-ergodic, has a very concrete form
 $$ \begin{gather*} m(E) = \frac{\int_E \psi_0\,d\mu}{\int_M \psi_0\,d\mu}, \end{gather*} $$
$$ \begin{gather*} m(E) = \frac{\int_E \psi_0\,d\mu}{\int_M \psi_0\,d\mu}, \end{gather*} $$
where
![]() $\psi _0$
is the eigenfunction of the
$\psi _0$
is the eigenfunction of the
![]() $L^2(\mu )$
-adjoint semigroup
$L^2(\mu )$
-adjoint semigroup
![]() $\left \{U_t^*: t \geqslant 0 \right \}$
for the eigenvalue
$\left \{U_t^*: t \geqslant 0 \right \}$
for the eigenvalue
![]() $e^{-\lambda _0 t}$
. In the context of Schrödinger operators and their semigroups,
$e^{-\lambda _0 t}$
. In the context of Schrödinger operators and their semigroups,
![]() $\lambda _0$
is the ground state eigenvalue, and
$\lambda _0$
is the ground state eigenvalue, and
![]() $\psi _0$
is the corresponding eigenfunction (for the adjoint). If
$\psi _0$
is the corresponding eigenfunction (for the adjoint). If
![]() $\psi _0 \in L^1(\mu )$
, the measure m is a finite measure, and it is a quasi-stationary (or quasi-invariant) measure of the semigroup
$\psi _0 \in L^1(\mu )$
, the measure m is a finite measure, and it is a quasi-stationary (or quasi-invariant) measure of the semigroup
![]() $\left \{U_t: t \geqslant 0 \right \}$
.
$\left \{U_t: t \geqslant 0 \right \}$
.
Since we do not assume that ![]() – that is, we do not assume conservativeness – we can expect only some kind of quasi-ergodic behavior. This is reflected in the structure of (1.1) where we normalize
– that is, we do not assume conservativeness – we can expect only some kind of quasi-ergodic behavior. This is reflected in the structure of (1.1) where we normalize
![]() $\sigma (U_t f)$
by the total mass
$\sigma (U_t f)$
by the total mass ![]() ; if
; if
![]() $U_t$
is the transition semigroup of some non-conservative stochastic process with initial distribution
$U_t$
is the transition semigroup of some non-conservative stochastic process with initial distribution
![]() $\sigma $
, this can be seen as conditioning on survival, – that is,
$\sigma $
, this can be seen as conditioning on survival, – that is, ![]() ,
,
![]() $\zeta = \inf \{s> 0 : X_s\notin M\}$
being the life-time.
$\zeta = \inf \{s> 0 : X_s\notin M\}$
being the life-time.
Large time evolution phenomena occur in various areas of mathematics and science (e.g., in PDEs, dynamical systems, stochastic processes, statistical and quantum physics), and they are often modeled by semigroups of operators. These applications require quite different state spaces, ranging from discrete spaces (lattices, graphs, …) to manifolds, fractals and, of course, classical Euclidean spaces. In order to cover these situations, we work in a rather general setting, on a locally compact Polish space N and
![]() $\mu $
is a locally finite Borel measure on the Borel sets
$\mu $
is a locally finite Borel measure on the Borel sets
![]() $\mathcal {B}(M)$
, and we consider sufficiently regular (but not necessarily self-adjoint or normal) operator semigroups acting (initially) on
$\mathcal {B}(M)$
, and we consider sufficiently regular (but not necessarily self-adjoint or normal) operator semigroups acting (initially) on
![]() $L^2(M,\mu )$
This includes the most interesting case when M is unbounded and/or
$L^2(M,\mu )$
This includes the most interesting case when M is unbounded and/or
![]() $\mu $
is an infinite measure. We consider semigroups of compact integral operators which are positivity improving and ultracontractive, and have the strong Feller property – see (
A0)–(
A3) and (
A4) in Section 2 for a precise statement. This framework accomodates many situations which are typically discussed in the literature.
$\mu $
is an infinite measure. We consider semigroups of compact integral operators which are positivity improving and ultracontractive, and have the strong Feller property – see (
A0)–(
A3) and (
A4) in Section 2 for a precise statement. This framework accomodates many situations which are typically discussed in the literature.
We focus on Schrödinger semigroups – with confining potentials, based both on local (second order differential operators) [Reference Davies and Simon16, Reference Davies15, Reference Simon58, Reference Simon57, Reference Sikora56, Reference Metafune, Pallara and Rhandi42, Reference Metafune and Spina43] and non-local kinetic term operators (Lévy operators, fractional and relativistic Laplacians, etc.) [Reference Carmona, Masters and Simon6, Reference Jacob and Wang22, Reference Kulczycki and Siudeja36, Reference Kwaśnicki and Mucha39, Reference Chen, Kim and Wang8, Reference Kaleta and Lőrinczi25, Reference Kaleta and Schilling26] – and on Feynman–Kac semigroups of Markov processes whose state spaces are general locally compact Polish spaces; this includes processes on fractals [Reference Fukushima19, Reference Kusuoka37] and Markov chains on graphs and discrete spaces [Reference Barlow4, Reference Cygan, Kaleta and Śliwiński14, Reference Murugan and Saloff-Coste46, Reference Murugan and Saloff-Coste47]. Some specific cases and various examples are discussed in Section 7. There are many other examples that fit into our framework, but which we do not discuss here in detail (e.g., evolution semigroups of non-homogeneous second order differential operators (generating diffusion processes) and non-local Lévy-type operators (generating jump Lévy-type processes) with confining coefficients [Reference Bakry, Gentil and Ledoux1, Reference El45, Reference El and Rhandi44, Reference Wang64, Reference Shiozawa and Wang55] or Markov processes killed upon exiting an unbounded domain [Reference Bañuelos and van den Berg3, Reference Kwaśnicki38, Reference Chen, Kim and Wang8, Reference Chen, Kim and Wang9]).
We are aware of only a few papers that work in a similar direction: Takeda [Reference Takeda62], Knobloch and Partzsch [Reference Knobloch and Partzsch31] and Zhang, Li and Song [Reference Zhang, Li and Song65]. Takeda uses a Dirichlet form approach, his processes and semigroups are symmetric and his main objective is the existence and uniqueness of the quasi-invariant measure. The key technical assumption is a tightness condition on the resolvent (kernel) of the semigroup; this is, essentially, a compactness condition which is weaker than IUC (intrinsic ultracontractivity). The contributions by Knobloch and Partzsch and Zhang et al. are, in some sense, extremes: Knobloch and Partzsch strive for a high level of generality in the basic setup, starting from a general Markov kernel assuming what they call ‘compact domination’. In the end, they prove that intrinsic ultracontractivity (IUC) implies uniform quasi-ergodicity at an exponential rate. One should mention that the only known examples satisfying the compact dominaton property are IUC kernels and semigroups. However, Zhang, Li and Song consider Markov processes; they are topologically quite general, but assume that the underlying measure is finite.
From the point of view of applications, both IUC and the finiteness of the underlying measure are rather restrictive conditions; for Schrödinger semigroups with confining potentials, IUC requires very fast growth of the potential at infinity; see [Reference Davies and Simon16, Reference Bañuelos2, Reference Kaleta and Lőrinczi25, Reference Chen and Wang10]. For non-self-adjoint operators, IUC was first studied by Kim and Song [Reference Kim and Song29, Reference Kim and Song30].
Recently, we introduced in [Reference Kaleta and Schilling26] the notion of progressive intrinsic ultracontractivity in order to obtain sharp two-sided heat kernel estimates for non-IUC or not necessarily IUC semigroups; see also Definition 4.2 and Remark 4.3 further down. As it turns out, it is this notion that helps us to avoid IUC as well as the finiteness of the underlying base measure. Consequently, we are able to characterize the quasi-ergodic regularity for a fairly general class of compact semigroups and underlying state spaces, including necessary and sufficient conditions for the existence and uniqueness of a quasi-stationary measure.
Let us briefly summarize the main contributions of this paper. Recall that the heat content is defined as ![]() .
.
Finite heat content and exponential quasi-ergodicity
We begin with a fairly general, yet easily verified, sufficient condition on the semigroup
![]() $\left \{U_t: t\geqslant 0\right \}$
such that the convergence in (1.1) is exponential in time, uniform for
$\left \{U_t: t\geqslant 0\right \}$
such that the convergence in (1.1) is exponential in time, uniform for
![]() $f\in L^p$
,
$f\in L^p$
,
![]() $\|f\|_p\leqslant 1$
, for any fixed
$\|f\|_p\leqslant 1$
, for any fixed
![]() $p \in [1,\infty ]$
, and it holds for any finite measure
$p \in [1,\infty ]$
, and it holds for any finite measure
![]() $\sigma $
. In fact (cf. Theorem 3.4), if the heat content of the semigroup is finite for some
$\sigma $
. In fact (cf. Theorem 3.4), if the heat content of the semigroup is finite for some
![]() $t_1>0$
, then
$t_1>0$
, then
![]() $\psi _0$
is integrable, the measure m is the unique quasi-stationary measure of the semigroup and the first term appearing in (1.1) is dominated by
$\psi _0$
is integrable, the measure m is the unique quasi-stationary measure of the semigroup and the first term appearing in (1.1) is dominated by ![]() – here,
– here,
![]() $t\gg 1$
is large, the constants
$t\gg 1$
is large, the constants
![]() $c_1, c_2>0$
do not depend on
$c_1, c_2>0$
do not depend on
![]() $\sigma $
or
$\sigma $
or
![]() $f \in L^p$
, and
$f \in L^p$
, and
![]() $\phi _0$
is the ground state of
$\phi _0$
is the ground state of
![]() $\left \{U_t: t \geqslant 0 \right \}$
. A similar reasoning applies to the adjoint semigroup
$\left \{U_t: t \geqslant 0 \right \}$
. A similar reasoning applies to the adjoint semigroup
![]() $\left \{U_t^*: t \geqslant 0 \right \}$
. Taking
$\left \{U_t^*: t \geqslant 0 \right \}$
. Taking
![]() $\sigma (dy)= \delta _{x}(dy)$
as the Dirac-delta measure concentrated in
$\sigma (dy)= \delta _{x}(dy)$
as the Dirac-delta measure concentrated in
![]() $x \in M$
, we obtain pointwise convergence with an explicit space-rate which is uniform on compact sets; see Corollary 3.5. We will see in Section 7.1 that for a very general class of Feynman–Kac semigroups with potential
$x \in M$
, we obtain pointwise convergence with an explicit space-rate which is uniform on compact sets; see Corollary 3.5. We will see in Section 7.1 that for a very general class of Feynman–Kac semigroups with potential
![]() $V(x)$
, the heat content
$V(x)$
, the heat content
![]() $Z(t_1)$
is finite if the function
$Z(t_1)$
is finite if the function
![]() $\exp (-t_1 V(x))$
is integrable ‘at infinity’; this condition is often also a necessary condition. This means that the finiteness of the heat content is independent of the underlying Markov process. Since our proof relies only on the Feynman–Kac formula (see Demuth and van Casteren [Reference Demuth and van Casteren17]), it also applies to evolution semigroups of very general Schrödinger operators
$\exp (-t_1 V(x))$
is integrable ‘at infinity’; this condition is often also a necessary condition. This means that the finiteness of the heat content is independent of the underlying Markov process. Since our proof relies only on the Feynman–Kac formula (see Demuth and van Casteren [Reference Demuth and van Casteren17]), it also applies to evolution semigroups of very general Schrödinger operators
![]() $H=-L+V$
– in this case, the finiteness of the heat content is determined solely by the behavior of the potential V at infinity, and it is independent of the kinetic term (i.e., the free Feller operator L).
$H=-L+V$
– in this case, the finiteness of the heat content is determined solely by the behavior of the potential V at infinity, and it is independent of the kinetic term (i.e., the free Feller operator L).
By definition, the heat content is finite if ![]() is integrable. The latter is guaranteed by the asymptotic ground state domination (aGSD) of the semigroup (that is,
is integrable. The latter is guaranteed by the asymptotic ground state domination (aGSD) of the semigroup (that is, ![]() for some
for some
![]() $t>0$
) and the integrability of the ground state
$t>0$
) and the integrability of the ground state
![]() $\phi _0$
. In [Reference Kaleta and Schilling26], we defined the notion of progressive ground state domination (pGSD), which requires only that
$\phi _0$
. In [Reference Kaleta and Schilling26], we defined the notion of progressive ground state domination (pGSD), which requires only that ![]() for some increasing family of compact sets
for some increasing family of compact sets
![]() $K_t\uparrow M$
. In [Reference Kaleta and Schilling26], pGSD was obtained as a necessary condition of sharp two-sided heat kernel estimates for Schrödinger semigroups; we will now see that pGSD is closely related to quasi-ergodicity.
$K_t\uparrow M$
. In [Reference Kaleta and Schilling26], pGSD was obtained as a necessary condition of sharp two-sided heat kernel estimates for Schrödinger semigroups; we will now see that pGSD is closely related to quasi-ergodicity.
Equivalence of aGSD/pGSD and quasi-ergodicity
If pGSD holds for some family of compact sets
![]() $K_t\uparrow M$
, one can show that (1.1) is dominated by some rate
$K_t\uparrow M$
, one can show that (1.1) is dominated by some rate
![]() $\kappa (t)$
which is essentially given by decay of
$\kappa (t)$
which is essentially given by decay of ![]() and
and ![]() for
for
![]() $x\notin K_{bt}$
(for some fixed
$x\notin K_{bt}$
(for some fixed
![]() $b\in (0,1/2)$
). In fact, the bound
$b\in (0,1/2)$
). In fact, the bound
![]() $\kappa (t)$
is uniform for all
$\kappa (t)$
is uniform for all
![]() $f\in L^p(\mu )$
,
$f\in L^p(\mu )$
,
![]() $\|f\|_p\leqslant 1$
, and all measures
$\|f\|_p\leqslant 1$
, and all measures
![]() $\sigma $
with support in
$\sigma $
with support in
![]() $K_{at}$
(where
$K_{at}$
(where
![]() $a\in (0,1)$
such that
$a\in (0,1)$
such that
![]() $a+2b=1$
); see Theorem 5.2. Specializing again to
$a+2b=1$
); see Theorem 5.2. Specializing again to
![]() $\sigma = \delta _x$
with
$\sigma = \delta _x$
with
![]() $x\in K_{at}$
, we see in Theorem 5.4 that pGSD is equivalent to the convergence of (1.1) to zero (locally uniformly for
$x\in K_{at}$
, we see in Theorem 5.4 that pGSD is equivalent to the convergence of (1.1) to zero (locally uniformly for
![]() $x\in K_{t}$
) as
$x\in K_{t}$
) as
![]() $t\to \infty $
. The latter property is best described as ‘progressive uniform quasi-ergodicity’. As a consequence (see Theorem 5.5), we also see that the quasi-ergodic measure is necessarily given by m, resp.,
$t\to \infty $
. The latter property is best described as ‘progressive uniform quasi-ergodicity’. As a consequence (see Theorem 5.5), we also see that the quasi-ergodic measure is necessarily given by m, resp.,
![]() $m^*$
, hence it is unique.
$m^*$
, hence it is unique.
In Section 4, we see that the finiteness of the heat content always implies pGSD, but without good control on the growth of the family of compact sets
![]() $K_t\uparrow M$
. In this connection, it is interesting to compare Theorem 3.4 and Theorems 5.2 and 5.4. Theorem 3.4 gives an easy-to-check sufficient condition (to wit: finite heat content) for the exponential (in time) quasi-ergodicity, but we may not be able to control the space behavior. Theorem 5.2 and 5.4 contain a necessary and sufficient condition (to wit: pGSD) for a somewhat stronger property, which is progressively uniform in space, and with a time-rate depending on the semigroup. The examples in Section 7.3 illustrate that the finiteness of the heat content requires stronger assumptions on the generator – for instance, for Schrödinger or Feynman–Kac semigroups, one needs that the potential V grows at infinity at least logarithmically.
$K_t\uparrow M$
. In this connection, it is interesting to compare Theorem 3.4 and Theorems 5.2 and 5.4. Theorem 3.4 gives an easy-to-check sufficient condition (to wit: finite heat content) for the exponential (in time) quasi-ergodicity, but we may not be able to control the space behavior. Theorem 5.2 and 5.4 contain a necessary and sufficient condition (to wit: pGSD) for a somewhat stronger property, which is progressively uniform in space, and with a time-rate depending on the semigroup. The examples in Section 7.3 illustrate that the finiteness of the heat content requires stronger assumptions on the generator – for instance, for Schrödinger or Feynman–Kac semigroups, one needs that the potential V grows at infinity at least logarithmically.
Assuming that the heat content is finite, our methods also yield results on the asymptotics of compact semigroups and the heat content as
![]() $t\to \infty $
; cf. Section 6. For example, one can see that
$t\to \infty $
; cf. Section 6. For example, one can see that
![]() $Z(t)$
is exponentially close to
$Z(t)$
is exponentially close to
![]() $e^{-\lambda _0 t}\|\phi _0\|_1\|\psi _0\|_1/\mu (\psi _0\phi _0)$
as
$e^{-\lambda _0 t}\|\phi _0\|_1\|\psi _0\|_1/\mu (\psi _0\phi _0)$
as
![]() $t\to \infty $
; see Corollary 6.2.
$t\to \infty $
; see Corollary 6.2.
The final section (Section 7) contains a number of examples which illustrate the applicability and the limitations of our results from the previous sections. The examples in 7.1 are related to Theorem 3.4 and Corollary 3.5, and the examples in Sections 7.2 and 7.3 mainly illustrate the pGSD-property from Theorems 5.2 and 5.4. In fact, Section 7.3 contains a complete characterization, giving necessary and sufficient conditions, of quasi-ergodic regularity of the Schrödinger semigroups corresponding to a large class of non-local Schrödinger operators with confining potentials; this can be seen as a direct continuation of our recent work [Reference Kaleta and Schilling26].
Notation. Most of our notation is standard or self-explanatory. We use ‘positive’ in the non-strict sense (e.g., a function
![]() $f \in L^2(M,\mu )$
is called positive if
$f \in L^2(M,\mu )$
is called positive if
![]() $f \geqslant 0$
$f \geqslant 0$
![]() $\mu $
-a.e.), and we say that f is ‘strictly positive’ if
$\mu $
-a.e.), and we say that f is ‘strictly positive’ if
![]() $f> 0$
$f> 0$
![]() $\mu $
-a.e. We will frequently use the shorthand
$\mu $
-a.e. We will frequently use the shorthand
![]() $m(f)$
to denote
$m(f)$
to denote
![]() $\int f\,dm$
. We use
$\int f\,dm$
. We use
![]() $a\wedge b$
and
$a\wedge b$
and
![]() $a\vee b$
to indicate
$a\vee b$
to indicate
![]() $\min (a,b)$
and
$\min (a,b)$
and
![]() $\max (a,b)$
, and we write
$\max (a,b)$
, and we write
![]() $f\asymp g$
if
$f\asymp g$
if
![]() $c^{-1} f(x)\leqslant g(x)\leqslant c g(x)$
for all x (in a given range) and with some fixed constant
$c^{-1} f(x)\leqslant g(x)\leqslant c g(x)$
for all x (in a given range) and with some fixed constant
![]() $c\in (0,\infty )$
. Finally, we call a strongly continuous contraction semigroup
$c\in (0,\infty )$
. Finally, we call a strongly continuous contraction semigroup
![]() $\left \{U_t: t\geqslant 0\right \}$
a Feller semigroup if it maps the continuous functions vanishing at infinity,
$\left \{U_t: t\geqslant 0\right \}$
a Feller semigroup if it maps the continuous functions vanishing at infinity,
![]() $C_\infty (M)$
into itself, and a strong Feller semigroup if it maps the bounded Borel measurable functions
$C_\infty (M)$
into itself, and a strong Feller semigroup if it maps the bounded Borel measurable functions
![]() $B_b(M)$
(or, sometimes, the set
$B_b(M)$
(or, sometimes, the set
![]() $L^\infty (M)$
) into the bounded continuous functions
$L^\infty (M)$
) into the bounded continuous functions
![]() $C_b(M)$
.
$C_b(M)$
.
2. Setup and basic assumptions
Topological preliminaries
For the convenience of our readers, we summarize a few topological preliminaries with references. We will work in a Polish space M (i.e., a completely metrizable topological space such that the metric defines the topology, and the topology has a countable base (second countable)). Being a metric space, M is also first countable (each point has a countable neighborhood basis), and it is separable (i.e., it contains a countable dense subset); cf. [Reference Engelking18, Corollary 1.3.8, Theorem 4.1.15]. We call M locally compact if each
![]() $x\in M$
has a relatively compact open neighborhood
$x\in M$
has a relatively compact open neighborhood
![]() $U(x)$
. If a Polish space is locally compact, it is
$U(x)$
. If a Polish space is locally compact, it is
![]() $\sigma $
-compact (or countable at infinity) (i.e., there is an increasing sequence of compact sets
$\sigma $
-compact (or countable at infinity) (i.e., there is an increasing sequence of compact sets
![]() $K_n$
such that
$K_n$
such that
![]() $\bigcup _{n\in \mathbb {N}} K_n = M$
); cf. [Reference Engelking18, Theorem 4.1.15.iii)]. In a metric space, compact sets are closed, and
$\bigcup _{n\in \mathbb {N}} K_n = M$
); cf. [Reference Engelking18, Theorem 4.1.15.iii)]. In a metric space, compact sets are closed, and
![]() $\sigma $
-compactness allows us to write any closed set as a countable union of compact sets. Therefore, the Borel
$\sigma $
-compactness allows us to write any closed set as a countable union of compact sets. Therefore, the Borel
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal B(M)$
of a locally compact Polish space is generated by the compact sets. A Borel measure
$\mathcal B(M)$
of a locally compact Polish space is generated by the compact sets. A Borel measure
![]() $\mu $
is a positive measure defined on the Borel sets
$\mu $
is a positive measure defined on the Borel sets
![]() $\mathcal B(M)$
. It is locally finite if each point
$\mathcal B(M)$
. It is locally finite if each point
![]() $x\in M$
has an open neighborhood with finite measure. This implies that
$x\in M$
has an open neighborhood with finite measure. This implies that
![]() $\mu $
is finite on compact sets. Thus, a locally finite measure on a locally compact Polish space is
$\mu $
is finite on compact sets. Thus, a locally finite measure on a locally compact Polish space is
![]() $\sigma $
-finite.
$\sigma $
-finite.
Setting and assumptions
Throughout, we assume that M is a locally compact Polish space and
![]() $\mu $
a positive, locally finite Borel measure with full topological support. We do not assume that the space M is compact or that the measure
$\mu $
a positive, locally finite Borel measure with full topological support. We do not assume that the space M is compact or that the measure
![]() $\mu $
is finite. On
$\mu $
is finite. On
![]() $L^2(M,\mu )$
, we consider a strongly continuous semigroup of bounded linear operators,
$L^2(M,\mu )$
, we consider a strongly continuous semigroup of bounded linear operators,
![]() $\left \{U_t: t \geqslant 0 \right \}$
and its adjoint semigroup
$\left \{U_t: t \geqslant 0 \right \}$
and its adjoint semigroup
![]() $\left \{U_t^*: t \geqslant 0 \right \}$
, which is given by
$\left \{U_t^*: t \geqslant 0 \right \}$
, which is given by
Moreover, we assume that
![]() $U_t$
and
$U_t$
and
![]() $U_t^*$
are integral operators, which are given by a real-valued measurable kernel
$U_t^*$
are integral operators, which are given by a real-valued measurable kernel
![]() $u_t(x,y)$
:
$u_t(x,y)$
:
Moreover, we use the following assumptions:
Assumptions.
 $$\begin{align} &\text{For some } t_0> 0, \text{ the operator } U_{t_0} \text{ is positivity improving: for every positive }\notag\\ & f \in L^2(M,\mu), f\not\equiv 0, \text{ we have } U_{t_0} f(x) > 0 \text{ for } \mu\text{-almost all } x\in M. \end{align}$$
$$\begin{align} &\text{For some } t_0> 0, \text{ the operator } U_{t_0} \text{ is positivity improving: for every positive }\notag\\ & f \in L^2(M,\mu), f\not\equiv 0, \text{ we have } U_{t_0} f(x) > 0 \text{ for } \mu\text{-almost all } x\in M. \end{align}$$
 $$\begin{align} &\text{The semigroups } \left\{U_t: t \geqslant 0 \right\} \text{ and } \left\{U_t^*: t \geqslant 0 \right\} \text{ have the strong Feller property:}\notag\\ &\text{ for every } t>0 \text{ and } f \in L^{\infty}(M,\mu), \text{ we have } U_t f, U_{t}^*f \in C_b(M); \end{align}$$
$$\begin{align} &\text{The semigroups } \left\{U_t: t \geqslant 0 \right\} \text{ and } \left\{U_t^*: t \geqslant 0 \right\} \text{ have the strong Feller property:}\notag\\ &\text{ for every } t>0 \text{ and } f \in L^{\infty}(M,\mu), \text{ we have } U_t f, U_{t}^*f \in C_b(M); \end{align}$$
 $$\begin{align} &\text{For some } t_0>0, \text{ the operators } U_{t_0}, U_{t_0}^*: L^2(M,\mu) \to L^{\infty}(M,\mu) \text{ are bounded }\notag\\ &\text{(i.e.,ultracontractive):}\\ &\qquad\qquad\displaystyle\int u^2_{t_0}(\cdot,y) \,\mu(dy) \in L^{\infty}(M,\mu) \quad \text{and} \quad \int u^2_{t_0}(x,\cdot) \,\mu(dx) \in L^{\infty}(M,\mu).\notag \end{align}$$
$$\begin{align} &\text{For some } t_0>0, \text{ the operators } U_{t_0}, U_{t_0}^*: L^2(M,\mu) \to L^{\infty}(M,\mu) \text{ are bounded }\notag\\ &\text{(i.e.,ultracontractive):}\\ &\qquad\qquad\displaystyle\int u^2_{t_0}(\cdot,y) \,\mu(dy) \in L^{\infty}(M,\mu) \quad \text{and} \quad \int u^2_{t_0}(x,\cdot) \,\mu(dx) \in L^{\infty}(M,\mu).\notag \end{align}$$
Our results in Sections 4 and 5 need, when considering non-compact spaces M, a further strong decay condition.

Let us comment on the assumptions ( A0)–( A4) and how they are related.
Remark 2.1. (
A0) is equivalent to assuming that the adjoint operators
![]() $U_t^*$
are compact on
$U_t^*$
are compact on
![]() $(L^2(M,\mu ))^* = L^2(M,\mu )$
.
$(L^2(M,\mu ))^* = L^2(M,\mu )$
.
(
A1) is equivalent to assuming that
![]() $U_{t_0}^*$
is positivity improving for some
$U_{t_0}^*$
is positivity improving for some
![]() $t_0>0$
. Moreover,
$t_0>0$
. Moreover,
![]() $U_{t_0}$
and
$U_{t_0}$
and
![]() $U_{t_0}^*$
are positivity improving if, and only if, the integral kernel
$U_{t_0}^*$
are positivity improving if, and only if, the integral kernel
![]() $u_{t_0}(x,y)$
is for
$u_{t_0}(x,y)$
is for
![]() $\mu \otimes \mu $
almost all
$\mu \otimes \mu $
almost all
![]() $(x,y)$
strictly positive.
$(x,y)$
strictly positive.
(
A2) is equivalent to the condition that ![]() and
and ![]() are bounded continuous functions of x. These functions will play a central role in our investigations.
are bounded continuous functions of x. These functions will play a central role in our investigations.
(
A3) implies, because of the reflexivity of the space
![]() $L^2(M,\mu )$
, that (the restrictions of the second duals to
$L^2(M,\mu )$
, that (the restrictions of the second duals to
![]() $L^1(M,\mu ) \subset \big (L^{\infty }(M,\mu )\big )^*$
of) the operators
$L^1(M,\mu ) \subset \big (L^{\infty }(M,\mu )\big )^*$
of) the operators
![]() $U_{t_0}$
and
$U_{t_0}$
and
![]() $U^*_{t_0}$
are bounded operators from
$U^*_{t_0}$
are bounded operators from
![]() $L^1(M,\mu )$
to
$L^1(M,\mu )$
to
![]() $L^2(M,\mu )$
. Due to the semigroup property, the operators
$L^2(M,\mu )$
. Due to the semigroup property, the operators
![]() $U_{2t_0}$
and
$U_{2t_0}$
and
![]() $U^*_{2t_0}$
are bounded operators from
$U^*_{2t_0}$
are bounded operators from
![]() $L^1(M,\mu )$
to
$L^1(M,\mu )$
to
![]() $L^{\infty }(M,\mu )$
; this is equivalent to saying
$L^{\infty }(M,\mu )$
; this is equivalent to saying
Using the semigroup property, these boundedness properties extend to all
![]() $t \geqslant t_0$
, resp.
$t \geqslant t_0$
, resp.
![]() $t \geqslant 2 t_0$
. Conversely, if there is some
$t \geqslant 2 t_0$
. Conversely, if there is some
![]() $t_0>0$
, for which (2.2) holds, then the condition (
A3) is also satisfied.
$t_0>0$
, for which (2.2) holds, then the condition (
A3) is also satisfied.
Let
![]() $t>2t_0$
. From (
A2), we know that
$t>2t_0$
. From (
A2), we know that
![]() $U_t$
and
$U_t$
and
![]() $U_t^*$
are continuous operators from
$U_t^*$
are continuous operators from
![]() $L^\infty (M,\mu )\to L^\infty (M,\mu )$
, and (
A3) means that
$L^\infty (M,\mu )\to L^\infty (M,\mu )$
, and (
A3) means that
![]() $U_t$
and
$U_t$
and
![]() $U_t^*$
are continuous operators from
$U_t^*$
are continuous operators from
![]() $L^2(M,\mu )\to L^\infty (M,\mu )$
; by duality, we see that
$L^2(M,\mu )\to L^\infty (M,\mu )$
; by duality, we see that
![]() $U_t$
and
$U_t$
and
![]() $U_t^*$
map
$U_t^*$
map
![]() $L^1(M,\mu )$
continuously into
$L^1(M,\mu )$
continuously into
![]() $L^2(M,\mu )$
, and using again (
A3) and the semigroup property, we conclude that
$L^2(M,\mu )$
, and using again (
A3) and the semigroup property, we conclude that
![]() $U_t$
and
$U_t$
and
![]() $U_t^*$
are continuous from
$U_t^*$
are continuous from
![]() $L^1(M,\mu )$
into
$L^1(M,\mu )$
into
![]() $L^\infty (M,\mu )$
. Therefore, a standard interpolation argument shows that
$L^\infty (M,\mu )$
. Therefore, a standard interpolation argument shows that
![]() $U_t$
and
$U_t$
and
![]() $U_t^*$
are continuous
$U_t^*$
are continuous
![]() $L^p(M,\mu )\to L^\infty (M,\mu )$
for any
$L^p(M,\mu )\to L^\infty (M,\mu )$
for any
![]() $p\in (1,\infty )$
and, in view of (
A2), we also have
$p\in (1,\infty )$
and, in view of (
A2), we also have
Let A, and
![]() $A^*$
, denote the generators of semigroups
$A^*$
, denote the generators of semigroups
![]() $\left \{U_t: t \in T \right \}$
, and
$\left \{U_t: t \in T \right \}$
, and
![]() $\left \{U_t^*: t \geqslant 0 \right \}$
, respectively. A version of the Jentzsch theorem (see [Reference Schaefer50, Theorem V.6.6]) shows that
$\left \{U_t^*: t \geqslant 0 \right \}$
, respectively. A version of the Jentzsch theorem (see [Reference Schaefer50, Theorem V.6.6]) shows that
![]() $\lambda _0:= \inf \mathop {\mathrm {Re}} \big ( \operatorname {\mathrm {Spec}} (-A)\big ) = \inf \mathop {\mathrm {Re}} \big (\operatorname {\mathrm {Spec}} (-A^*)\big )$
is common isolated and simple eigenvalue of
$\lambda _0:= \inf \mathop {\mathrm {Re}} \big ( \operatorname {\mathrm {Spec}} (-A)\big ) = \inf \mathop {\mathrm {Re}} \big (\operatorname {\mathrm {Spec}} (-A^*)\big )$
is common isolated and simple eigenvalue of
![]() $-A$
and
$-A$
and
![]() $-A^*$
. Moreover, the corresponding normalized eigenfunctions
$-A^*$
. Moreover, the corresponding normalized eigenfunctions
![]() $\phi _0, \psi _0 \in L^2(M,\mu )$
can be assumed to be strictly positive. In particular,
$\phi _0, \psi _0 \in L^2(M,\mu )$
can be assumed to be strictly positive. In particular,
The number
![]() $\lambda _0$
is called the ground state eigenvalue, and the functions
$\lambda _0$
is called the ground state eigenvalue, and the functions
![]() $\phi _0, \psi _0$
, are the ground states of
$\phi _0, \psi _0$
, are the ground states of
![]() $-A$
, and
$-A$
, and
![]() $-A^*$
, respectively.
$-A^*$
, respectively.
By (2.3), we have
![]() $\phi _0, \psi _0 \in C_b(M)$
, and both eigenequations in (2.4) are also true in a pointwise sense. We will frequently use the following constant
$\phi _0, \psi _0 \in C_b(M)$
, and both eigenequations in (2.4) are also true in a pointwise sense. We will frequently use the following constant
and set
As mentioned above,
![]() $\mu (\mathcal {N})=0$
. Due to the continuity of
$\mu (\mathcal {N})=0$
. Due to the continuity of
![]() $\phi _0$
and
$\phi _0$
and
![]() $\psi _0$
, the set
$\psi _0$
, the set
![]() $\mathcal {N}$
is a closed set. If for some
$\mathcal {N}$
is a closed set. If for some
![]() $t>0$
, the kernel
$t>0$
, the kernel
![]() $u_t(x,y)$
is defined pointwise (e.g., if the map
$u_t(x,y)$
is defined pointwise (e.g., if the map
![]() $(x,y) \mapsto u_t(x,y)$
is continuous) and strictly positive for all
$(x,y) \mapsto u_t(x,y)$
is continuous) and strictly positive for all
![]() $x,y \in M$
, then
$x,y \in M$
, then
![]() $\mathcal {N} = \emptyset $
. We are mainly interested in examples which come from the theory of stochastic processes, and for these examples,
$\mathcal {N} = \emptyset $
. We are mainly interested in examples which come from the theory of stochastic processes, and for these examples,
![]() $\mathcal {N} = \emptyset $
is always satisfied. Since the original question comes from the
$\mathcal {N} = \emptyset $
is always satisfied. Since the original question comes from the
![]() $L^2$
-theory, we do not want to assume a priori
$L^2$
-theory, we do not want to assume a priori
![]() $\mathcal {N} = \emptyset $
.
$\mathcal {N} = \emptyset $
.
The following result is a straightforward adaptation of a Lemma by Zhang, Li and Song [Reference Zhang, Li and Song65, Lemma 2.1]; it is a variant of the estimate which was originally obtained for intrinsic semigroups by Kim and Song [Reference Kim and Song28, Theorem 2.7]. The very first result in this direction is due to Pinsky [Reference Pinsky48, Theorem 3] for diffusion semigroups on bounded domains in
![]() $\mathbb {R}^d$
. The result of Zhang et al. is valid for rather general nonsymmetric semigroups. These authors use sub-Markovian semigroups of standard Markov processes with strictly positive kernels of Hilbert-Schmidt type satisfying (
A3). A close inspection of their proof reveals that only the compactness of the operators
$\mathbb {R}^d$
. The result of Zhang et al. is valid for rather general nonsymmetric semigroups. These authors use sub-Markovian semigroups of standard Markov processes with strictly positive kernels of Hilbert-Schmidt type satisfying (
A3). A close inspection of their proof reveals that only the compactness of the operators
![]() $U_t$
and
$U_t$
and
![]() $U^*_t$
is needed and that the result is valid in the more general setting, which is described by our present conditions (
A0)–(
A3). Note that Zhang et al. use
$U^*_t$
is needed and that the result is valid in the more general setting, which is described by our present conditions (
A0)–(
A3). Note that Zhang et al. use
![]() $t_0=1$
and that their proof requires
$t_0=1$
and that their proof requires
![]() $t/2> 1 = t_0$
.
$t/2> 1 = t_0$
.
Lemma 2.2 [Reference Zhang, Li and Song65, Lemma 2.1]
If (
A0)–(
A3) hold for some
![]() $t_0>0$
, then there exist
$t_0>0$
, then there exist
![]() $C, \gamma> 0$
such that
$C, \gamma> 0$
such that
This estimate leads to a rate of convergence (as
![]() $t\to \infty $
) for compact semigroups, which can be seen as a variant of the classical result of Chavel and Karp [Reference Chavel and Karp7]; see also [Reference Simon59, Reference Keller, Lenz, Vogt and Wojciechowski27].
$t\to \infty $
) for compact semigroups, which can be seen as a variant of the classical result of Chavel and Karp [Reference Chavel and Karp7]; see also [Reference Simon59, Reference Keller, Lenz, Vogt and Wojciechowski27].
Unless otherwise stated, we take the same ![]() in (
A1), (
A3) and (
A4).
in (
A1), (
A3) and (
A4).
We will now briefly discuss the relation between ( A4) and ( A0).
Lemma 2.3. Assume (
A2) and (
A3), (
A4) for some
![]() $t_0>0$
. Then the operators
$t_0>0$
. Then the operators
![]() $U_t, U_t^*: L^2(M,\mu ) \to L^2(M,\mu )$
are compact for all
$U_t, U_t^*: L^2(M,\mu ) \to L^2(M,\mu )$
are compact for all
![]() $t \geqslant t_0$
. In particular, if (
A3), (
A4) are true for every
$t \geqslant t_0$
. In particular, if (
A3), (
A4) are true for every
![]() $t_0>0$
, then (
A0) holds.
$t_0>0$
, then (
A0) holds.
Proof. We consider only the operators
![]() $U_t$
. The proof for
$U_t$
. The proof for
![]() $U^*_t$
is similar. For a compact set
$U^*_t$
is similar. For a compact set
![]() $K \subset M$
, we define
$K \subset M$
, we define
(i.e.,
![]() $U_t^K$
is an integral operator with the kernel
$U_t^K$
is an integral operator with the kernel ![]() ). Observe that by (
A3),
). Observe that by (
A3),
 $$ \begin{align*} \int_M\int_M u^K_t(x,y)^2 \,\mu(dy)\,\mu(dx) & = \int_K\int_M u_t(x,y)^2 \,\mu(dy)\,\mu(dx) \\ & \leqslant \mu(K) \cdot {\mathrm{ess\ sup}}_{x \in M} \int_M u_t(x,y)^2 \,\mu(dy) < \infty, \quad t \geqslant t_0, \end{align*} $$
$$ \begin{align*} \int_M\int_M u^K_t(x,y)^2 \,\mu(dy)\,\mu(dx) & = \int_K\int_M u_t(x,y)^2 \,\mu(dy)\,\mu(dx) \\ & \leqslant \mu(K) \cdot {\mathrm{ess\ sup}}_{x \in M} \int_M u_t(x,y)^2 \,\mu(dy) < \infty, \quad t \geqslant t_0, \end{align*} $$
which means that
![]() $U^K_t$
,
$U^K_t$
,
![]() $t \geqslant t_0$
, are Hilbert–Schmidt operators. Moreover, for
$t \geqslant t_0$
, are Hilbert–Schmidt operators. Moreover, for
![]() $f \in L^2(M,\mu )$
, by the Cauchy–Schwarz inequality and the Tonelli theorem,
$f \in L^2(M,\mu )$
, by the Cauchy–Schwarz inequality and the Tonelli theorem,

The assumptions (
A2) and (
A4) yield that for every
![]() $t> t_0$
and
$t> t_0$
and
![]() $\epsilon>0$
, we can find a compact set K such that
$\epsilon>0$
, we can find a compact set K such that
Letting
![]() $\epsilon \to 0$
, we see that every operator
$\epsilon \to 0$
, we see that every operator
![]() $U_t$
,
$U_t$
,
![]() $t \geqslant t_0$
, is a strong limit of compact operators, and hence compact. This completes the proof.
$t \geqslant t_0$
, is a strong limit of compact operators, and hence compact. This completes the proof.
If the operators
![]() $U_t$
,
$U_t$
,
![]() $t>0$
, are self-adjoint, then compactness for some
$t>0$
, are self-adjoint, then compactness for some
![]() $t>0$
implies compactness for every
$t>0$
implies compactness for every
![]() $t>0$
– this is due to spectral theorem. In that case, (
A4) implies (
A0), even if (
A3), (
A4) are true for some
$t>0$
– this is due to spectral theorem. In that case, (
A4) implies (
A0), even if (
A3), (
A4) are true for some
![]() $t_0>0$
only. For non-self-adjoint operators, this is not clear. Therefore, in Sections 4 and 5, we have to assume both (
A0) and (
A4).
$t_0>0$
only. For non-self-adjoint operators, this is not clear. Therefore, in Sections 4 and 5, we have to assume both (
A0) and (
A4).
In unbounded spaces, it is often true that (
A0) and (
A4) (holding for all
![]() $t_0>0$
) are equivalent see, for example, [Reference Kwaśnicki38, Lemma 1] and [Reference Kaleta and Kulczycki23, Lemma 9]. Some general sufficient conditions for compactness in various settings, including Markov, Schrödinger and Feynman–Kac semigroups, and more general perturbations can be found in [Reference Wang and Wu63, Reference Takeda, Tawara and Tsuchida61, Reference Lenz, Stollmann and Wingert40].
$t_0>0$
) are equivalent see, for example, [Reference Kwaśnicki38, Lemma 1] and [Reference Kaleta and Kulczycki23, Lemma 9]. Some general sufficient conditions for compactness in various settings, including Markov, Schrödinger and Feynman–Kac semigroups, and more general perturbations can be found in [Reference Wang and Wu63, Reference Takeda, Tawara and Tsuchida61, Reference Lenz, Stollmann and Wingert40].
3. Heat content and exponential quasi-ergodicity of compact semigroups
If
![]() $\phi _0, \psi _0 \in L^1(M,\mu )$
,Footnote 1 we can define probability measures on
$\phi _0, \psi _0 \in L^1(M,\mu )$
,Footnote 1 we can define probability measures on
![]() $(M,\mathcal {B}(M))$
by
$(M,\mathcal {B}(M))$
by
 $$ \begin{align} m(E) = \frac{\int_E \psi_0(x)\,\mu(dx)}{\int_M \psi_0(x)\,\mu(dx)} \quad\text{and}\quad m^*(E) = \frac{\int_E \phi_0(x)\,\mu(dx)}{\int_M \phi_0(x)\,\mu(dx)}. \end{align} $$
$$ \begin{align} m(E) = \frac{\int_E \psi_0(x)\,\mu(dx)}{\int_M \psi_0(x)\,\mu(dx)} \quad\text{and}\quad m^*(E) = \frac{\int_E \phi_0(x)\,\mu(dx)}{\int_M \phi_0(x)\,\mu(dx)}. \end{align} $$
It is rather easy to check that the measures m and
![]() $m^*$
are quasi-stationary (probability) measures of the semigroups
$m^*$
are quasi-stationary (probability) measures of the semigroups
![]() $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
.
$\left \{U^*_t: t \geqslant 0 \right \}$
.
Definition 3.1 (Quasi-stationary measure on
 $L^{\infty }$
)
$L^{\infty }$
)
Let (
A2) hold. A probability measure
![]() $\bar m$
on
$\bar m$
on
![]() $(M,\mathcal {B}(M))$
is said to be a quasi-stationary measure of the semigroup
$(M,\mathcal {B}(M))$
is said to be a quasi-stationary measure of the semigroup
![]() $\left \{U_t: t \geqslant 0 \right \}$
(on
$\left \{U_t: t \geqslant 0 \right \}$
(on
![]() $L^{\infty }(M,\mu )$
), if for all
$L^{\infty }(M,\mu )$
), if for all
![]() $t>0$
and
$t>0$
and
![]() $f \in L^{\infty }(M,\mu )$
, we have
$f \in L^{\infty }(M,\mu )$
, we have ![]() and
and

Because of (2.3) – this follows from (
A2), (
A3) – we can extend the definition of quasi-stationarity to
![]() $L^p(M,\mu )$
for any
$L^p(M,\mu )$
for any
![]() $p \in [1,\infty )$
, at least for large t.
$p \in [1,\infty )$
, at least for large t.
Lemma 3.2. Assume (
A1)–(
A3) for
![]() $t_0>0$
and let
$t_0>0$
and let
![]() $p \in [1,\infty )$
. Let
$p \in [1,\infty )$
. Let
![]() $\bar m$
be a probability measure on
$\bar m$
be a probability measure on
![]() $(M,\mathcal {B}(M))$
and let
$(M,\mathcal {B}(M))$
and let
![]() $t> 2t_0$
be such that
$t> 2t_0$
be such that ![]() . Then
. Then

Proof. Fix
![]() $p \in [1,\infty )$
and
$p \in [1,\infty )$
and
![]() $t> 2t_0$
. It is enough to show both implications for non-negative functions.
$t> 2t_0$
. It is enough to show both implications for non-negative functions.
‘
![]() $\Leftarrow $
’ Let
$\Leftarrow $
’ Let
![]() $0 \leqslant g \in L^p(M,\mu )$
and
$0 \leqslant g \in L^p(M,\mu )$
and
![]() $f_n := g \wedge n \in L^{\infty }(M,\mu )$
,
$f_n := g \wedge n \in L^{\infty }(M,\mu )$
,
![]() $n \in \mathbb {N}$
. We have
$n \in \mathbb {N}$
. We have
![]() $f_n \uparrow g$
as
$f_n \uparrow g$
as
![]() $n \to \infty $
,
$n \to \infty $
, ![]() ,
,
![]() $n \in \mathbb {N}$
, and the implication follows with the monotone convergence theorem.
$n \in \mathbb {N}$
, and the implication follows with the monotone convergence theorem.
‘
![]() $\Rightarrow $
’ Let
$\Rightarrow $
’ Let
![]() $0 \leqslant f \in L^{\infty }(M,\mu )$
and set
$0 \leqslant f \in L^{\infty }(M,\mu )$
and set ![]() ,
,
![]() $n \in \mathbb {N}$
, where
$n \in \mathbb {N}$
, where
![]() $(K_n)$
is an increasing sequence of compact sets such that
$(K_n)$
is an increasing sequence of compact sets such that
![]() $\bigcup _{n\in \mathbb {N}} K_n = M$
; see the discussion of topological preliminaries at the beginning of Section 2. We have
$\bigcup _{n\in \mathbb {N}} K_n = M$
; see the discussion of topological preliminaries at the beginning of Section 2. We have
![]() $g_n \uparrow f$
as
$g_n \uparrow f$
as
![]() $n \to \infty $
,
$n \to \infty $
, ![]() ,
,
![]() $n \in \mathbb {N}$
, and we use monotone convergence once again.
$n \in \mathbb {N}$
, and we use monotone convergence once again.
If (
A3) holds for any
![]() $t_0>0$
, then it also makes sense to speak about quasi-stationarity on
$t_0>0$
, then it also makes sense to speak about quasi-stationarity on
![]() $L^p$
,
$L^p$
,
![]() $p<\infty $
, for all
$p<\infty $
, for all
![]() $t>0$
. In particular, the implications in Lemma 3.2 hold true for every
$t>0$
. In particular, the implications in Lemma 3.2 hold true for every
![]() $t>0$
.
$t>0$
.
We come back to the measures
![]() $m, m^*$
defined in (3.1). Here, the condition (3.2) reads
$m, m^*$
defined in (3.1). Here, the condition (3.2) reads
Since we assume that
![]() $\phi _0, \psi _0 \in L^{\infty }(M,\mu )$
, (3.3) remains valid for
$\phi _0, \psi _0 \in L^{\infty }(M,\mu )$
, (3.3) remains valid for
![]() $f\in L^p(M,\mu )$
,
$f\in L^p(M,\mu )$
,
![]() $p \in [1,\infty ]$
. This can be easily seen without Lemma 3.2. Indeed, it follows from the Hölder inequality and the fact that
$p \in [1,\infty ]$
. This can be easily seen without Lemma 3.2. Indeed, it follows from the Hölder inequality and the fact that
![]() $\phi _0, \psi _0 \in L^1(M,\mu ) \cap L^{\infty }(M,\mu ) \subset L^q(M,\mu )$
for any
$\phi _0, \psi _0 \in L^1(M,\mu ) \cap L^{\infty }(M,\mu ) \subset L^q(M,\mu )$
for any
![]() $q \in [1,\infty ]$
.
$q \in [1,\infty ]$
.
Our arguments in Sections 3 and 5 are based on the following observation, which is a direct consequence of the estimate in Lemma 2.2.
Lemma 3.3. Let (
A0)–(
A3) hold for some
![]() $t_0>0$
and denote by
$t_0>0$
and denote by
![]() $C,\gamma $
the constants appearing in Lemma 2.2. For every
$C,\gamma $
the constants appearing in Lemma 2.2. For every
![]() $0 \leqslant s, r < t$
with
$0 \leqslant s, r < t$
with
![]() $t-s-r> 2 t_0$
$t-s-r> 2 t_0$
holds true with the function

Proof. If
![]() $s=r=0$
, this is just the estimate from Lemma 2.2. We will only work out the case
$s=r=0$
, this is just the estimate from Lemma 2.2. We will only work out the case
![]() $s,r>0$
. The remaining two cases follow with very similar arguments. Using the eigenequations
$s,r>0$
. The remaining two cases follow with very similar arguments. Using the eigenequations
and the Chapman-Kolmogorov identities, we see that
 $$ \begin{align*} &e^{\lambda_0 t} u_t(x,y) - (1/\Lambda) \phi_0(x) \psi_0(y) \\ &= e^{\lambda_0 s} \int_M u_s(x,z) \left[e^{\lambda_0 (t-s)} u_{t-s}(z,y) - (1/\Lambda) \phi_0(z) \psi_0(y) \right]\mu(dz) \\ &= e^{\lambda_0 s} \int_M u_s(x,z) \left[e^{\lambda_0 r}\int_M \left[e^{\lambda_0 (t-s-r)} u_{t-s-r}(z,w)\right.\right. \\ &\quad \left.\left.\vphantom{\int} - (1/\Lambda) \phi_0(z) \psi_0(w) \right] u_r(w,y) \,\mu(dw) \right]\mu(dz). \end{align*} $$
$$ \begin{align*} &e^{\lambda_0 t} u_t(x,y) - (1/\Lambda) \phi_0(x) \psi_0(y) \\ &= e^{\lambda_0 s} \int_M u_s(x,z) \left[e^{\lambda_0 (t-s)} u_{t-s}(z,y) - (1/\Lambda) \phi_0(z) \psi_0(y) \right]\mu(dz) \\ &= e^{\lambda_0 s} \int_M u_s(x,z) \left[e^{\lambda_0 r}\int_M \left[e^{\lambda_0 (t-s-r)} u_{t-s-r}(z,w)\right.\right. \\ &\quad \left.\left.\vphantom{\int} - (1/\Lambda) \phi_0(z) \psi_0(w) \right] u_r(w,y) \,\mu(dw) \right]\mu(dz). \end{align*} $$
By Lemma 2.2, we have
which gives
 $$ \begin{align*} &\left|e^{\lambda_0 t} u_t(x,y) - (1/\Lambda) \phi_0(x) \psi_0(y)\right| \\ &\qquad\leqslant C e^{-\gamma (t-s-r)} \left(e^{\lambda_0 s} \int_M u_s(x,z) \,\mu(dz) \right) \left(e^{\lambda_0 r} \int_M u_r(w,y) \,\mu(dw)\right). \end{align*} $$
$$ \begin{align*} &\left|e^{\lambda_0 t} u_t(x,y) - (1/\Lambda) \phi_0(x) \psi_0(y)\right| \\ &\qquad\leqslant C e^{-\gamma (t-s-r)} \left(e^{\lambda_0 s} \int_M u_s(x,z) \,\mu(dz) \right) \left(e^{\lambda_0 r} \int_M u_r(w,y) \,\mu(dw)\right). \end{align*} $$
This is the claimed bound.
Our next theorem is the first main result of this section. It relates the exponential quasi-ergodicity of the semigroups
![]() $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
with the finiteness of their heat content. It also shows that the corresponding quasi-stationary probability distributions are unique. Recall that
$\left \{U^*_t: t \geqslant 0 \right \}$
with the finiteness of their heat content. It also shows that the corresponding quasi-stationary probability distributions are unique. Recall that
is the heat content of
![]() $\left \{U_t: t \geqslant 0 \right \}$
or
$\left \{U_t: t \geqslant 0 \right \}$
or
![]() $\left \{U_t^*: t \geqslant 0 \right \}$
. In general,
$\left \{U_t^*: t \geqslant 0 \right \}$
. In general,
![]() $Z(t) \in (0,\infty ]$
. For each
$Z(t) \in (0,\infty ]$
. For each
![]() $t>0$
, the condition
$t>0$
, the condition
![]() $Z(t) < \infty $
is equivalent to the boundedness of the operators
$Z(t) < \infty $
is equivalent to the boundedness of the operators
![]() $U_t, U^*_{t}: L^{\infty }(M,\mu ) \to L^1(M,\mu )$
.
$U_t, U^*_{t}: L^{\infty }(M,\mu ) \to L^1(M,\mu )$
.
Unless otherwise stated, we use the value ![]() from Lemma 3.3 in all further statements as well as for the assumptions (
A1), (
A3) and (
A4), and
from Lemma 3.3 in all further statements as well as for the assumptions (
A1), (
A3) and (
A4), and
![]() $\mathcal {N}$
denotes the exceptional set defined in (2.5).
$\mathcal {N}$
denotes the exceptional set defined in (2.5).
Theorem 3.4. Let M be a locally compact Polish space and assume that (
A0)–(
A3) hold. If there exists some
![]() $t_1 \geqslant t_0$
such that the heat content is finite, that is,
$t_1 \geqslant t_0$
such that the heat content is finite, that is,
then we have the following:
-
a)
 $\phi _0, \psi _0 \in L^1(M,\mu )$
and both measures m and
$\phi _0, \psi _0 \in L^1(M,\mu )$
and both measures m and
 $m^*$
in (3.1) are well defined.
$m^*$
in (3.1) are well defined. -
b) For every
 $p \in [1,\infty ]$
, there exists
$p \in [1,\infty ]$
, there exists
 $C>0$
such that for every finite measure
$C>0$
such that for every finite measure
 $\sigma $
on M with
$\sigma $
on M with
 $\operatorname {\mathrm {supp}} \sigma \cap (M \setminus \mathcal {N}) \neq \emptyset $
, we have for all
$\operatorname {\mathrm {supp}} \sigma \cap (M \setminus \mathcal {N}) \neq \emptyset $
, we have for all
 $t>6t_1$
and
$t>6t_1$
and
 $t_1 \leqslant s \leqslant t/2$
, and
$t_1 \leqslant s \leqslant t/2$
, and

-
c) The measures m and
 $m^*$
are the unique quasi-stationary probability measures of
$m^*$
are the unique quasi-stationary probability measures of
 $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
 $\left \{U^*_t: t \geqslant 0 \right \}$
, respectively, such that
$\left \{U^*_t: t \geqslant 0 \right \}$
, respectively, such that
 $m(M\setminus \mathcal {N})\cdot m^*(M\setminus \mathcal {N})>0$
.
$m(M\setminus \mathcal {N})\cdot m^*(M\setminus \mathcal {N})>0$
.
Proof. Recall that ![]() ,
,
![]() $t \geqslant t_1$
. Thus, a) follows from the inequalities
$t \geqslant t_1$
. Thus, a) follows from the inequalities ![]() and
and ![]() ,
,
![]() $x \in M$
,
$x \in M$
,
![]() $t>0$
.
$t>0$
.
We prove b) only for the semigroup
![]() $\left \{U_t: t \geqslant 0 \right \}$
. The proof for
$\left \{U_t: t \geqslant 0 \right \}$
. The proof for
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
is literally the same. Let
$\left \{U^*_t: t \geqslant 0 \right \}$
is literally the same. Let
![]() $p \in [1,\infty ]$
and let
$p \in [1,\infty ]$
and let
![]() $\sigma $
be a finite measure on M such that
$\sigma $
be a finite measure on M such that
![]() $\operatorname {\mathrm {supp}} \sigma \cap (M \setminus \mathcal {N}) \neq \emptyset $
. Note that
$\operatorname {\mathrm {supp}} \sigma \cap (M \setminus \mathcal {N}) \neq \emptyset $
. Note that ![]() and
and ![]() ,
,
![]() $t>0$
. For every
$t>0$
. For every
![]() $f \in L^p(M,\mu )$
and
$f \in L^p(M,\mu )$
and
![]() $t>6t_1$
(in particular,
$t>6t_1$
(in particular,
![]() $t-t_1-s>2t_0$
), we may write
$t-t_1-s>2t_0$
), we may write

Since for all
![]() $x \in M$
,
$x \in M$
,
 $$ \begin{align*} &e^{\lambda_0 t}U_t f(x) - (1/\Lambda) \, \phi_0(x) \int_M f(y) \psi_0(y) \,\mu(dy)\\ &\qquad = \int_M f(y) \left(e^{\lambda_0 t}u_t(x,y) - (1/\Lambda) \, \phi_0(x) \psi_0(y)\right) \mu(dy), \end{align*} $$
$$ \begin{align*} &e^{\lambda_0 t}U_t f(x) - (1/\Lambda) \, \phi_0(x) \int_M f(y) \psi_0(y) \,\mu(dy)\\ &\qquad = \int_M f(y) \left(e^{\lambda_0 t}u_t(x,y) - (1/\Lambda) \, \phi_0(x) \psi_0(y)\right) \mu(dy), \end{align*} $$
and

we can apply Lemma 3.3 (with
![]() $t_1 \leqslant s \leqslant t/2$
and
$t_1 \leqslant s \leqslant t/2$
and
![]() $r=t_1$
) and integrate with respect to
$r=t_1$
) and integrate with respect to
![]() $\sigma $
to get
$\sigma $
to get

and

Note that

This gives

with
![]() $\widetilde C := C e^{(\lambda _0+\eta ) t_1} \left \|\phi _0\right \|_{\infty }$
, where
$\widetilde C := C e^{(\lambda _0+\eta ) t_1} \left \|\phi _0\right \|_{\infty }$
, where
![]() $C,\gamma $
are the constants from Lemma 3.3. Finally, by the Hölder inequality,
$C,\gamma $
are the constants from Lemma 3.3. Finally, by the Hölder inequality,

where q and p are conjugate exponents. Notice that ![]() and
and
![]() $\left \|\psi _0\right \|_q < \infty $
. Indeed, if
$\left \|\psi _0\right \|_q < \infty $
. Indeed, if
![]() $p=1$
, then
$p=1$
, then
![]() $q=\infty $
, and the claim follows from (
A2) and (
A3) combined with (2.4). If
$q=\infty $
, and the claim follows from (
A2) and (
A3) combined with (2.4). If
![]() $p=\infty $
and
$p=\infty $
and
![]() $q=1$
, then the claim follows from the fact that
$q=1$
, then the claim follows from the fact that ![]() and from a). If
and from a). If
![]() $1 < p < \infty $
, then also
$1 < p < \infty $
, then also
![]() $1< q < \infty $
, and we have
$1< q < \infty $
, and we have
and
This completes the proof of b).
In order to show c), assume that both m and
![]() $\bar m$
are quasi-stationary probability measures and
$\bar m$
are quasi-stationary probability measures and
![]() $\operatorname {\mathrm {supp}} \bar m \cap (M \setminus \mathcal {N}) \neq \emptyset $
. Since
$\operatorname {\mathrm {supp}} \bar m \cap (M \setminus \mathcal {N}) \neq \emptyset $
. Since
![]() $\bar m$
is finite, we can use
$\bar m$
is finite, we can use
![]() $\bar m = \sigma $
in Part b) and we get, because of the quasi-stationary property (3.2),
$\bar m = \sigma $
in Part b) and we get, because of the quasi-stationary property (3.2),

(uniformly) for all
![]() $f\in L^\infty (M,\mu )$
with
$f\in L^\infty (M,\mu )$
with
![]() $\|f\|_{\infty }\leqslant 1$
. By our assumptions,
$\|f\|_{\infty }\leqslant 1$
. By our assumptions,
![]() $\mu $
has full topological support, it is locally finite – hence finite on all compact sets – and the compact sets generate the Borel
$\mu $
has full topological support, it is locally finite – hence finite on all compact sets – and the compact sets generate the Borel
![]() $\sigma $
-algebra on M. Moreover, M is
$\sigma $
-algebra on M. Moreover, M is
![]() $\sigma $
-compact (i.e., there is an increasing sequence of compact sets
$\sigma $
-compact (i.e., there is an increasing sequence of compact sets
![]() $K_n$
such that
$K_n$
such that
![]() $M = \bigcup _{n\geqslant 1}K_n$
). Taking
$M = \bigcup _{n\geqslant 1}K_n$
). Taking ![]() for any compact set K, we conclude that
for any compact set K, we conclude that
![]() $m = \bar m$
first on the compact sets and, using the standard uniqueness theorem for measures, on all Borel sets. The proof of the uniqueness of
$m = \bar m$
first on the compact sets and, using the standard uniqueness theorem for measures, on all Borel sets. The proof of the uniqueness of
![]() $m^*$
is similar.
$m^*$
is similar.
Corollary 3.5. Let M be a locally compact Polish space and assume that (
A0)–(
A3) hold, and assume that there exists some
![]() $t_1 \geqslant t_0$
such that
$t_1 \geqslant t_0$
such that
![]() $Z(t_1) < \infty $
.
$Z(t_1) < \infty $
.
Both semigroups
![]() $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
are quasi-ergodic with exponential time rate
$\left \{U^*_t: t \geqslant 0 \right \}$
are quasi-ergodic with exponential time rate
![]() $e^{-\gamma t}$
and space rates
$e^{-\gamma t}$
and space rates ![]() and
and ![]() , respectively. More precisely, for every
, respectively. More precisely, for every
![]() $p \in [1,\infty ]$
, there is a constant
$p \in [1,\infty ]$
, there is a constant
![]() $C>0$
such that for every
$C>0$
such that for every
![]() $f \in L^p(M,\mu )$
with
$f \in L^p(M,\mu )$
with
![]() $\left \|f\right \|_p \leqslant 1$
,
$\left \|f\right \|_p \leqslant 1$
,

and

Moreover, the measures m, and
![]() $m^*$
, are the only quasi-stationary measures of
$m^*$
, are the only quasi-stationary measures of
![]() $\left \{U_t: t \geqslant 0 \right \}$
, and
$\left \{U_t: t \geqslant 0 \right \}$
, and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
, respectively, such that
$\left \{U^*_t: t \geqslant 0 \right \}$
, respectively, such that
![]() $m(M\setminus \mathcal {N})\cdot m^*(M\setminus \mathcal {N})>0$
.
$m(M\setminus \mathcal {N})\cdot m^*(M\setminus \mathcal {N})>0$
.
Note that, since ![]() and
and
![]() $\phi _0$
,
$\phi _0$
,
![]() $\psi _0$
are continuous and strictly positive on M, the exponential quasi-ergodicity in Corollary 3.5 is uniform for all x in compact subsets of
$\psi _0$
are continuous and strictly positive on M, the exponential quasi-ergodicity in Corollary 3.5 is uniform for all x in compact subsets of
![]() $M \setminus \mathcal {N}$
.
$M \setminus \mathcal {N}$
.
If
![]() $\mu (M) < \infty $
, then the heat content is automatically finite for large times, and we recover some of the results from [Reference Zhang, Li and Song65].
$\mu (M) < \infty $
, then the heat content is automatically finite for large times, and we recover some of the results from [Reference Zhang, Li and Song65].
4. Progressive ground state domination and heat content
In this section, we will need the notions of hemi-compact space and exhausting family of sets.
Definition 4.1. Let M be a topological space. An exhausting family of compact sets is a family of compact sets
![]() $\left \{K_t \subset M : t \geqslant t_1\right \}$
(defined for some
$\left \{K_t \subset M : t \geqslant t_1\right \}$
(defined for some
![]() $t_1 \geqslant 0$
) such that
$t_1 \geqslant 0$
) such that
![]() $K_t \subset K_s$
, for every
$K_t \subset K_s$
, for every
![]() $t_1 \leqslant t < s$
and
$t_1 \leqslant t < s$
and
![]() $\bigcup _{t \geqslant t_1} K_t = M$
.
$\bigcup _{t \geqslant t_1} K_t = M$
.
The space M is called hemi-compact if there is an exhausting family of compact sets
![]() $\{K_t : t\geqslant t_1\}$
, and for every compact set
$\{K_t : t\geqslant t_1\}$
, and for every compact set
![]() $K \subset M$
, there exists some
$K \subset M$
, there exists some
![]() $t \geqslant t_1$
such that
$t \geqslant t_1$
such that
![]() $K \subset K_t$
.
$K \subset K_t$
.
Since M is a locally compact Polish space, M is hemi-compact; moreover, the concepts of
![]() $\sigma $
-compactness and hemi-compactness coincide in such spaces; see, for example, [Reference Engelking18, p. 195]. If M is compact, it is also hemi-compact with a trivial exhausting family
$\sigma $
-compactness and hemi-compactness coincide in such spaces; see, for example, [Reference Engelking18, p. 195]. If M is compact, it is also hemi-compact with a trivial exhausting family
![]() $\left \{K_t : t \geqslant t_1\right \}$
such that
$\left \{K_t : t \geqslant t_1\right \}$
such that
![]() $K_t=M$
for all
$K_t=M$
for all
![]() $t \geqslant t_1$
. Assume now that (
A0)–(
A3) hold with some
$t \geqslant t_1$
. Assume now that (
A0)–(
A3) hold with some
![]() $t_0>0$
. The following properties will be central to our investigations in this section.
$t_0>0$
. The following properties will be central to our investigations in this section.
Definition 4.2 (aGSD and pGSD)
Let
![]() $\left \{U_t: t \geqslant 0 \right \}$
be a semigroup of operators on
$\left \{U_t: t \geqslant 0 \right \}$
be a semigroup of operators on
![]() $L^2(M,\mu )$
satisfying the conditions (
A0)–(
A3) and let
$L^2(M,\mu )$
satisfying the conditions (
A0)–(
A3) and let
![]() $\lambda _0$
and
$\lambda _0$
and
![]() $\phi _0$
be the corresponding ground state eigenvalue and normalized eigenfunction.
$\phi _0$
be the corresponding ground state eigenvalue and normalized eigenfunction.
-
a) The semigroup
 $\left \{U_t: t \geqslant 0 \right \}$
is said to be asymptotically ground state dominated (aGSD, for short) if there exist constants
$\left \{U_t: t \geqslant 0 \right \}$
is said to be asymptotically ground state dominated (aGSD, for short) if there exist constants
 $C, t_1>0$
such that (4.1)
$C, t_1>0$
such that (4.1)
-
b) The semigroup
 $\left \{U_t: t \geqslant 0 \right \}$
is said to be progressively ground state dominated (pGSD, for short) if there exist constants
$\left \{U_t: t \geqslant 0 \right \}$
is said to be progressively ground state dominated (pGSD, for short) if there exist constants
 $C, t_1>0$
and an exhausting family of compact sets
$C, t_1>0$
and an exhausting family of compact sets
 $\left \{K_t : t \geqslant t_1\right \}$
such that (4.2)
$\left \{K_t : t \geqslant t_1\right \}$
such that (4.2)
Remark 4.3.
-
a) Because of the eigenequation
 $e^{-\lambda _0 t} \phi _0 = U_t \phi _0$
, there is some kind of reverse inequality to (4.1):
$e^{-\lambda _0 t} \phi _0 = U_t \phi _0$
, there is some kind of reverse inequality to (4.1):  ,
,
 $x \in M$
,
$x \in M$
,
 $t>0$
.
$t>0$
. -
b) Notice that both
 and
and
 $\phi _0(x)$
are continuous functions. Since
$\phi _0(x)$
are continuous functions. Since
 $\mu (\mathcal {N})=0$
and since
$\mu (\mathcal {N})=0$
and since
 $\mu $
charges every open set, the interior of
$\mu $
charges every open set, the interior of
 $\mathcal {N}$
is empty and
$\mathcal {N}$
is empty and
 $\overline {M\setminus \mathcal {N}}=M$
. This means that we can replace in (4.1) and (4.2) the condition ‘
$\overline {M\setminus \mathcal {N}}=M$
. This means that we can replace in (4.1) and (4.2) the condition ‘
 $x\in M$
’ by ‘
$x\in M$
’ by ‘
 $x\in M\setminus \mathcal {N}$
’.
$x\in M\setminus \mathcal {N}$
’. -
c) aGSD was studied in the papers [Reference Kaleta and Lőrinczi25, Reference Kaleta, Kwaśnicki and Lőrinczi24] in relation to intrinsic ultracontractivity and hypercontractivity. It is shown in [Reference Kaleta and Schilling26] that aGSD is a much more restrictive condition than the finiteness of heat content for large times. It follows directly from Lemma 3.3 that aGSD of
 $\left \{U_t: t \geqslant 0 \right \}$
implies
$\left \{U_t: t \geqslant 0 \right \}$
implies
 $\phi _0 \in L^1(M,\mu )$
as well as the finiteness of the heat content for large times; this is also true for
$\phi _0 \in L^1(M,\mu )$
as well as the finiteness of the heat content for large times; this is also true for
 $\left \{U^*_t: t \geqslant 0 \right \}$
and
$\left \{U^*_t: t \geqslant 0 \right \}$
and
 $\psi _0$
.
$\psi _0$
. -
d) pGSD was recently introduced in [Reference Kaleta and Schilling26] as a direct consequence of the concept of progressive intrinsic ultracontractivity (pIUC) for Schrödinger semigroups. In this and the next section, we will explain the impact of pGSD on the quasi-ergodic behavior of compact semigroups and discuss the relation between pGSD and the finiteness of the heat content.
-
e) From the definition, we see that aGSD always implies pGSD. Recall that
 ,
,  ,
,
 $\phi _0$
,
$\phi _0$
,
 $\psi _0 \in C_b(M)$
. If the space M is compact and
$\psi _0 \in C_b(M)$
. If the space M is compact and
 $\phi _0$
,
$\phi _0$
,
 $\psi _0$
are strictly positive everywhere (i.e.,
$\psi _0$
are strictly positive everywhere (i.e.,
 $\mathcal {N} = \emptyset $
), then
$\mathcal {N} = \emptyset $
), then
 $\inf _M \phi _0> 0$
and
$\inf _M \phi _0> 0$
and
 $\inf _M \psi _0> 0$
; therefore, aGSD always holds. In particular, pGSD holds with an exhausting family
$\inf _M \psi _0> 0$
; therefore, aGSD always holds. In particular, pGSD holds with an exhausting family
 $\left \{K_t : t \geqslant t_1\right \}$
such that
$\left \{K_t : t \geqslant t_1\right \}$
such that
 $K_t=M$
for all
$K_t=M$
for all
 $t \geqslant t_1$
.
$t \geqslant t_1$
.
We first show that aGSD of
![]() $\left \{U_t: t \geqslant 0 \right \}$
implies the exponential uniform (for the whole space M) quasi-ergodicity of this semigroup on every
$\left \{U_t: t \geqslant 0 \right \}$
implies the exponential uniform (for the whole space M) quasi-ergodicity of this semigroup on every
![]() $L^p(M,\mu )$
,
$L^p(M,\mu )$
,
![]() $p \geqslant 1$
; as before, this also holds for
$p \geqslant 1$
; as before, this also holds for
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
. In particular, this gives a relatively short and elementary proof of the main results of [Reference Knobloch and Partzsch31, Theorem 1, Corollary 2] in our framework. We also have some converse statement.
$\left \{U^*_t: t \geqslant 0 \right \}$
. In particular, this gives a relatively short and elementary proof of the main results of [Reference Knobloch and Partzsch31, Theorem 1, Corollary 2] in our framework. We also have some converse statement.
Corollary 4.4. Let M be a general locally compact (but not necessarily compact) Polish space and assume that ( A0)–( A3) hold. Then we have the following assertions.
-
a) If the semigroup
 $\left \{U_t: t \geqslant 0 \right \}$
is aGSD for some
$\left \{U_t: t \geqslant 0 \right \}$
is aGSD for some
 $t_1 \geqslant t_0$
, then there is for every
$t_1 \geqslant t_0$
, then there is for every
 $p \in [1,\infty ]$
a constant
$p \in [1,\infty ]$
a constant
 $C>0$
, such that for every
$C>0$
, such that for every
 $f \in L^p(M,\mu )$
with
$f \in L^p(M,\mu )$
with
 $\left \|f\right \|_p \leqslant 1$
, (4.3)
$\left \|f\right \|_p \leqslant 1$
, (4.3)
-
b) If there is a constant
 $C>0$
such that then the semigroup
$C>0$
such that then the semigroup
 $\left \{U_t: t \geqslant 0 \right \}$
is aGSD.
$\left \{U_t: t \geqslant 0 \right \}$
is aGSD.
Both assertions a) and b) are also true for the semigroup
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
and the quasi-stationary measure
$\left \{U^*_t: t \geqslant 0 \right \}$
and the quasi-stationary measure
![]() $m^*$
. Under aGSD, the measures m, and
$m^*$
. Under aGSD, the measures m, and
![]() $m^*$
, are the only quasi-stationary measures of
$m^*$
, are the only quasi-stationary measures of
![]() $\left \{U_t: t \geqslant 0 \right \}$
, and
$\left \{U_t: t \geqslant 0 \right \}$
, and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
, respectively, such that
$\left \{U^*_t: t \geqslant 0 \right \}$
, respectively, such that
![]() $m(M\setminus \mathcal {N})\cdot m^*(M\setminus \mathcal {N})>0$
.
$m(M\setminus \mathcal {N})\cdot m^*(M\setminus \mathcal {N})>0$
.
Proof. Assertion a) follows directly from a combination of Remark 4.3.c) and Corollary 3.5. Let us show b). Because of the eigenequation
![]() $U_t \phi _0 = e^{-\lambda _0 t} \phi _0$
, we see that there is some
$U_t \phi _0 = e^{-\lambda _0 t} \phi _0$
, we see that there is some
![]() $t_1>0$
such that
$t_1>0$
such that

which implies

Since
![]() $C>0$
and both functions
$C>0$
and both functions
![]() $\phi _0$
and
$\phi _0$
and ![]() are bounded and continuous, this completes the proof.
are bounded and continuous, this completes the proof.
As explained in Remark 4.3.e), if the space M is compact (hence,
![]() $\mu (M) <\infty $
, due to the local finiteness of
$\mu (M) <\infty $
, due to the local finiteness of
![]() $\mu $
) and the ground states are everywhere strictly positive, the semigroups
$\mu $
) and the ground states are everywhere strictly positive, the semigroups
![]() $\left \{U_t: t \geqslant 0 \right \}$
,
$\left \{U_t: t \geqslant 0 \right \}$
,
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
are automatically aGSD, and the heat content is finite for large times. In particular, Corollary 4.4 implies that both semigroups are exponentially uniformly (on the whole space M) quasi-ergodic.
$\left \{U^*_t: t \geqslant 0 \right \}$
are automatically aGSD, and the heat content is finite for large times. In particular, Corollary 4.4 implies that both semigroups are exponentially uniformly (on the whole space M) quasi-ergodic.
If the space M is non-compact, then aGSD is a rather restrictive condition. However, as illustrated in [Reference Kaleta and Schilling26], one should expect that in this case, a wide range of non-aGSD compact semigroups are still pGSD. From now on, we focus on the quasi-ergodicity of pGSD semigroups in the setting of non-compact spaces.
We first show that the finiteness of the heat content implies pGSD for both
![]() $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
; consequently, we get progressive uniform quasi-ergodicity with an exponential time-rate. To do so, we need a lemma. To keep the proofs simple, we assume in Lemma 4.5 and Theorem 4.6 that
$\left \{U^*_t: t \geqslant 0 \right \}$
; consequently, we get progressive uniform quasi-ergodicity with an exponential time-rate. To do so, we need a lemma. To keep the proofs simple, we assume in Lemma 4.5 and Theorem 4.6 that
![]() $\mathcal {N} = \emptyset $
(i.e., that the ground states are everywhere strictly positive).
$\mathcal {N} = \emptyset $
(i.e., that the ground states are everywhere strictly positive).
Lemma 4.5. Let M be a locally compact, but not compact, Polish space. Assume that (
A0)–(
A4) hold,
![]() $\mathcal {N} = \emptyset $
, and let
$\mathcal {N} = \emptyset $
, and let
![]() $\left \{K_t : t \geqslant t_0\right \}$
be an exhausting family of compact sets in M. Set
$\left \{K_t : t \geqslant t_0\right \}$
be an exhausting family of compact sets in M. Set
 $$ \begin{gather*} h(t) := \min\left\{\inf_{x \in K_t} \phi_0(x),\inf_{x \in K_t} \psi_0(x) \right\}, \quad t \geqslant t_0, \end{gather*} $$
$$ \begin{gather*} h(t) := \min\left\{\inf_{x \in K_t} \phi_0(x),\inf_{x \in K_t} \psi_0(x) \right\}, \quad t \geqslant t_0, \end{gather*} $$
and consider the generalized inverse of h,
Define the function
![]() $\eta : [-\gamma ^{-1} \log h(t_0),\infty ) \to [t_0,\infty )$
by
$\eta : [-\gamma ^{-1} \log h(t_0),\infty ) \to [t_0,\infty )$
by
Then
![]() $\eta $
is increasing on
$\eta $
is increasing on
![]() $[-\gamma ^{-1}\log h(t_0),\infty )$
,
$[-\gamma ^{-1}\log h(t_0),\infty )$
,
![]() $\eta (t) \to \infty $
as
$\eta (t) \to \infty $
as
![]() $t \to \infty $
and
$t \to \infty $
and
 $$ \begin{gather*} e^{\gamma t} \min\left\{\inf_{x \in K_{\eta(t)}} \phi_0(x),\inf_{x \in K_{\eta(t)}} \psi_0(x) \right\} = e^{\gamma t} h(\eta(t)) = 1, \qquad t \geqslant -\gamma^{-1}\log h(t_0). \end{gather*} $$
$$ \begin{gather*} e^{\gamma t} \min\left\{\inf_{x \in K_{\eta(t)}} \phi_0(x),\inf_{x \in K_{\eta(t)}} \psi_0(x) \right\} = e^{\gamma t} h(\eta(t)) = 1, \qquad t \geqslant -\gamma^{-1}\log h(t_0). \end{gather*} $$
Proof. Because of the eigenequations, our assumptions (
A1)–(
A3) and
![]() $\mathcal {N}=\emptyset $
, the ground state eigenfunctions
$\mathcal {N}=\emptyset $
, the ground state eigenfunctions
![]() $\phi _0$
and
$\phi _0$
and
![]() $\psi _0$
are continuous and strictly positive on M. Together with the inequality in Remark 4.3.a) and the assumption (
A4), this implies that the function h is continuous, strictly positive and decreasing on
$\psi _0$
are continuous and strictly positive on M. Together with the inequality in Remark 4.3.a) and the assumption (
A4), this implies that the function h is continuous, strictly positive and decreasing on
![]() $[t_0,\infty )$
such that
$[t_0,\infty )$
such that
![]() $h(t) \to 0$
as
$h(t) \to 0$
as
![]() $t \uparrow \infty $
. In particular, its generalized inverse function
$t \uparrow \infty $
. In particular, its generalized inverse function
![]() $h^{-1}$
is decreasing on
$h^{-1}$
is decreasing on
![]() $(0,h(t_0)]$
,
$(0,h(t_0)]$
,
![]() $h^{-1}(s) \to \infty $
as
$h^{-1}(s) \to \infty $
as
![]() $s \downarrow 0$
, and we have
$s \downarrow 0$
, and we have
![]() $h(h^{-1}(s)) = s$
for every
$h(h^{-1}(s)) = s$
for every
![]() $s \in (0,h(t_0)]$
. Therefore,
$s \in (0,h(t_0)]$
. Therefore,
![]() $\eta $
is increasing on
$\eta $
is increasing on
![]() $[-\gamma ^{-1}\log h(t_0),\infty )$
as it is a composition of two decreasing functions
$[-\gamma ^{-1}\log h(t_0),\infty )$
as it is a composition of two decreasing functions
![]() $h^{-1}$
and
$h^{-1}$
and
![]() $t \mapsto e^{-\gamma t}$
,
$t \mapsto e^{-\gamma t}$
,
![]() $\eta (t) \to \infty $
as
$\eta (t) \to \infty $
as
![]() $t \to \infty $
, and
$t \to \infty $
, and
![]() $e^{\gamma t} h(\eta (t)) = e^{\gamma t} h(h^{-1}(e^{-\gamma t})) = e^{\gamma t} e^{-\gamma t} = 1$
. This completes the proof.
$e^{\gamma t} h(\eta (t)) = e^{\gamma t} h(h^{-1}(e^{-\gamma t})) = e^{\gamma t} e^{-\gamma t} = 1$
. This completes the proof.
In the following theorem, we will use the notation
![]() $\mathcal {M}^1(K)$
to denote all probability measures
$\mathcal {M}^1(K)$
to denote all probability measures
![]() $\sigma $
on
$\sigma $
on
![]() $(M,\mathcal {B}(M))$
such that
$(M,\mathcal {B}(M))$
such that
![]() $\operatorname {\mathrm {supp}}\sigma \subset K$
. Recall that we already know from Theorem 3.4 that the finiteness of the heat content for large times implies that
$\operatorname {\mathrm {supp}}\sigma \subset K$
. Recall that we already know from Theorem 3.4 that the finiteness of the heat content for large times implies that
![]() $\phi _0, \psi _0 \in L^1(M,\mu )$
and that the measures m, and
$\phi _0, \psi _0 \in L^1(M,\mu )$
and that the measures m, and
![]() $m^*$
, defined in (3.1) are the only quasi-stationary measures on each
$m^*$
, defined in (3.1) are the only quasi-stationary measures on each
![]() $L^p(M,\mu )$
,
$L^p(M,\mu )$
,
![]() $p \in [1,\infty ]$
, of the semigroups
$p \in [1,\infty ]$
, of the semigroups
![]() $\left \{U_t: t \geqslant 0 \right \}$
, and
$\left \{U_t: t \geqslant 0 \right \}$
, and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
, respectively.
$\left \{U^*_t: t \geqslant 0 \right \}$
, respectively.
Theorem 4.6. Let M be a locally compact, but not compact, Polish space. Assume that (
A0)–(
A4) hold, let
![]() $\left \{K_t : t \geqslant t_0\right \}$
be an exhausting family of compact sets in M, and assume that
$\left \{K_t : t \geqslant t_0\right \}$
be an exhausting family of compact sets in M, and assume that
![]() $\mathcal {N} = \emptyset $
. Set
$\mathcal {N} = \emptyset $
. Set
![]() $\widetilde t_0 = \max \left \{0, -\gamma ^{-1}\log h(t_0)\right \}$
and let
$\widetilde t_0 = \max \left \{0, -\gamma ^{-1}\log h(t_0)\right \}$
and let
![]() $\eta $
be the function defined in (4.4). If there is some
$\eta $
be the function defined in (4.4). If there is some
![]() $t_1 \geqslant t_0$
such that the heat content
$t_1 \geqslant t_0$
such that the heat content
![]() $Z(t_1) < \infty $
, then the following assertions hold.
$Z(t_1) < \infty $
, then the following assertions hold.
-
a) Both semigroups
 $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
 $\left \{U^*_t: t \geqslant 0 \right \}$
are pGSD for the exhausting family of sets
$\left \{U^*_t: t \geqslant 0 \right \}$
are pGSD for the exhausting family of sets
 $\left \{K_{\eta (t)} : t \geqslant \widetilde t_0\right \}$
.
$\left \{K_{\eta (t)} : t \geqslant \widetilde t_0\right \}$
. -
b) Both semigroups
 $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
 $\left \{U^*_t: t \geqslant 0 \right \}$
are exponentially progressively uniformly quasi-ergodic; that is, for every
$\left \{U^*_t: t \geqslant 0 \right \}$
are exponentially progressively uniformly quasi-ergodic; that is, for every
 $p \in [1,\infty ]$
, there exists some
$p \in [1,\infty ]$
, there exists some
 $C>0$
, such that and
$C>0$
, such that and

Proof. Recall that ![]() and
and ![]() . Since
. Since
![]() $Z(t_1) < \infty $
, this yields
$Z(t_1) < \infty $
, this yields
![]() $\phi _0, \psi _0 \in L^1(M,\mu )$
. Therefore, Lemma 3.3 (with
$\phi _0, \psi _0 \in L^1(M,\mu )$
. Therefore, Lemma 3.3 (with
![]() $s = 0$
and
$s = 0$
and
![]() $r=t_1$
) and Lemma 4.5 give
$r=t_1$
) and Lemma 4.5 give

for every
![]() $x \in K_{\eta (t)}$
and sufficiently large t; since the function
$x \in K_{\eta (t)}$
and sufficiently large t; since the function
![]() $\eta $
is increasing and
$\eta $
is increasing and
![]() $\eta (t) \to \infty $
as
$\eta (t) \to \infty $
as
![]() $t \to \infty $
, the family
$t \to \infty $
, the family
![]() $\left \{K_{\eta (t)} : t \geqslant \widetilde t_0\right \}$
is indeed exhausting. This gives
$\left \{K_{\eta (t)} : t \geqslant \widetilde t_0\right \}$
is indeed exhausting. This gives
for sufficiently large t, showing that the semigroup
![]() $\left \{U_t: t \geqslant 0 \right \}$
is pGSD. The pGSD property for the semigroup
$\left \{U_t: t \geqslant 0 \right \}$
is pGSD. The pGSD property for the semigroup
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
follows with exactly the same argument. This completes the proof of a).
$\left \{U^*_t: t \geqslant 0 \right \}$
follows with exactly the same argument. This completes the proof of a).
Part b) follows from Theorem 3.4.b) with
![]() $s = t/2$
and probability measures
$s = t/2$
and probability measures
![]() $\sigma $
supported in
$\sigma $
supported in
![]() $K_{\eta (t/2)}$
, by an application of the pGSD property which we have already established in Part a).
$K_{\eta (t/2)}$
, by an application of the pGSD property which we have already established in Part a).
5. Progressive ground state domination and quasi-ergodicity
As we have already noticed in the previous section, in a non-compact space M, aGSD is stronger than the finiteness of heat content for large times. However, the finiteness of the heat content for large times implies pGSD with a certain exhausting family of sets. Recall that these properties – aGSD, pGSD, finite heat content – automatically hold in compact spaces. Consequently, we also have uniform quasi-ergodicity at an exponential time-rate; see Remark 4.3.e), Corollary 4.4, and the comments following the corollary.
On the other hand, see [Reference Kaleta and Schilling26], pGSD is a general regularity property for compact non-aGSD semigroups, which can be studied on its own; in particular, pGSD is still true for a wide range of compact semigroups having infinite heat content for large times. In the present section, we follow this path, introducing the concept of progressive uniform quasi-ergodicity and studying its relation to pGSD.
Let
![]() $a,b \in (0,1)$
be arbitrary numbers such that
$a,b \in (0,1)$
be arbitrary numbers such that
![]() $a+2b=1$
. We show first that in a noncompact space M and under (
A4), pGSD for the exhausting family
$a+2b=1$
. We show first that in a noncompact space M and under (
A4), pGSD for the exhausting family
![]() $\left \{K_t : t \geqslant t_0\right \}$
implies progressive uniform quasi-ergodicity for the exhausting family
$\left \{K_t : t \geqslant t_0\right \}$
implies progressive uniform quasi-ergodicity for the exhausting family
![]() $\left \{K_{at} : t \geqslant t_0/a\right \}$
; the time-rate is given by
$\left \{K_{at} : t \geqslant t_0/a\right \}$
; the time-rate is given by
Note that
![]() $\kappa _b(t) \downarrow 0$
as
$\kappa _b(t) \downarrow 0$
as
![]() $t \uparrow \infty $
. Quite often (see the examples),
$t \uparrow \infty $
. Quite often (see the examples),
![]() $\kappa _b$
decays exponentially at infinity.
$\kappa _b$
decays exponentially at infinity.
We have to make sure that
![]() $\phi _0, \psi _0 \in L^1(M,\mu )$
, which means that both measures m and
$\phi _0, \psi _0 \in L^1(M,\mu )$
, which means that both measures m and
![]() $m^*$
in (3.1) are well defined. If the space M is compact, this follows from
$m^*$
in (3.1) are well defined. If the space M is compact, this follows from
![]() $\mu (M) < \infty $
and
$\mu (M) < \infty $
and
![]() $\phi _0, \psi _0 \in L^\infty (M,\mu )$
due to (
A3). For locally compact (but non-compact) Polish spaces M, this is still true under aGSD; see Remark 4.3.c). Now we show that
$\phi _0, \psi _0 \in L^\infty (M,\mu )$
due to (
A3). For locally compact (but non-compact) Polish spaces M, this is still true under aGSD; see Remark 4.3.c). Now we show that
![]() $\phi _0, \psi _0 \in L^1(M,\mu )$
holds if both semigroups
$\phi _0, \psi _0 \in L^1(M,\mu )$
holds if both semigroups
![]() $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
enjoy the pGSD property.
$\left \{U^*_t: t \geqslant 0 \right \}$
enjoy the pGSD property.
Lemma 5.1. Let M be a locally compact, but not compact, Polish space and assume (
A0)–(
A3). If the semigroups
![]() $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
are pGSD, then
$\left \{U^*_t: t \geqslant 0 \right \}$
are pGSD, then
![]() $\phi _0, \psi _0 \in L^1(M,\mu )$
.
$\phi _0, \psi _0 \in L^1(M,\mu )$
.
Proof. Suppose that pGSD holds for the exhausting family of compact sets
![]() $\left \{K_t : t \geqslant t_0\right \}$
. We only show that
$\left \{K_t : t \geqslant t_0\right \}$
. We only show that
![]() $\phi _0 \in L^1(M,\mu )$
. The proof for
$\phi _0 \in L^1(M,\mu )$
. The proof for
![]() $\psi _0$
is similar. By Lemma 3.3 (with
$\psi _0$
is similar. By Lemma 3.3 (with
![]() $t_0 < s < t$
such that
$t_0 < s < t$
such that
![]() $t-s> 2t_0$
and
$t-s> 2t_0$
and
![]() $r=0$
) and pGSD of
$r=0$
) and pGSD of
![]() $\left \{U_t: t \geqslant 0 \right \}$
, we have for
$\left \{U_t: t \geqslant 0 \right \}$
, we have for
![]() $\mu $
-almost all
$\mu $
-almost all
![]() $x \in K_s$
and
$x \in K_s$
and
![]() $y \in K_s \setminus \mathcal {N}$
$y \in K_s \setminus \mathcal {N}$

We integrate on both sides of the inequality in
![]() $x \in K_s$
and use pGSD of
$x \in K_s$
and use pGSD of
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
to get
$\left \{U^*_t: t \geqslant 0 \right \}$
to get

for sufficiently large t. Letting
![]() $t \to \infty $
, we obtain
$t \to \infty $
, we obtain
and monotone convergence finally proves
![]() $\phi _0 \in L^1(M,\mu )$
.
$\phi _0 \in L^1(M,\mu )$
.
Theorem 5.2. Let M be a locally compact, but not compact, Polish space. Assume that (
A0)–(
A4) hold and that both semigroups
![]() $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
are pGSD for the exhausting family of compact sets
$\left \{U^*_t: t \geqslant 0 \right \}$
are pGSD for the exhausting family of compact sets
![]() $\left \{K_t : t \geqslant t_0\right \}$
. Then we have
$\left \{K_t : t \geqslant t_0\right \}$
. Then we have
![]() $\phi _0, \psi _0 \in L^1(M,\mu )$
and, for every
$\phi _0, \psi _0 \in L^1(M,\mu )$
and, for every
![]() $a, b \in (0,1)$
such that
$a, b \in (0,1)$
such that
![]() $a+2b=1$
, both semigroups
$a+2b=1$
, both semigroups
![]() $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
are progressively uniformly quasi-ergodic for the exhausting family
$\left \{U^*_t: t \geqslant 0 \right \}$
are progressively uniformly quasi-ergodic for the exhausting family
![]() $\left \{K_{at} : t \geqslant t_0/a\right \}$
with time-rate
$\left \{K_{at} : t \geqslant t_0/a\right \}$
with time-rate
![]() $\kappa _b(t)$
given by (5.1); that is, for every
$\kappa _b(t)$
given by (5.1); that is, for every
![]() $p \in [1,\infty ]$
, there exists some
$p \in [1,\infty ]$
, there exists some
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $t>(4/(a \wedge b)) t_0$
,
$t>(4/(a \wedge b)) t_0$
,

and

Proof. In view of Lemma 5.1 we have
![]() $\phi _0, \psi _0 \in L^1(M,\mu )$
. We proceed as in the proof of Theorem 3.4. Since the proof for the dual semigroup is similar, we restrict our attention to
$\phi _0, \psi _0 \in L^1(M,\mu )$
. We proceed as in the proof of Theorem 3.4. Since the proof for the dual semigroup is similar, we restrict our attention to
![]() $\left \{U_t: t \geqslant 0 \right \}$
. Fix
$\left \{U_t: t \geqslant 0 \right \}$
. Fix
![]() $p \in [1,\infty ]$
. For every
$p \in [1,\infty ]$
. For every
![]() $f \in L^p(M,\mu )$
, all
$f \in L^p(M,\mu )$
, all
![]() $t>(4/(a \wedge b)) t_0$
and
$t>(4/(a \wedge b)) t_0$
and
![]() $\sigma \in \mathcal {M}^1(K_{at})$
such that
$\sigma \in \mathcal {M}^1(K_{at})$
such that
![]() $\operatorname {\mathrm {supp}} \sigma \cap (M \setminus \mathcal {N}) \neq \emptyset $
, we have
$\operatorname {\mathrm {supp}} \sigma \cap (M \setminus \mathcal {N}) \neq \emptyset $
, we have

as well as
 $$ \begin{align} \begin{aligned} &e^{\lambda_0 t}U_t f(x) - (1/\Lambda) \, \phi_0(x) \int_M f(y) \psi_0(y) \,\mu(dy) \\ &\quad= \int_M \left(e^{\lambda_0 t}u_t(x,y) - (1/\Lambda) \, \phi_0(x) \psi_0(y)\right) f(y) \,\mu(dy), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &e^{\lambda_0 t}U_t f(x) - (1/\Lambda) \, \phi_0(x) \int_M f(y) \psi_0(y) \,\mu(dy) \\ &\quad= \int_M \left(e^{\lambda_0 t}u_t(x,y) - (1/\Lambda) \, \phi_0(x) \psi_0(y)\right) f(y) \,\mu(dy), \end{aligned} \end{align} $$
and

We first estimate (5.3). With the Chapman–Kolmogorov equation and the eigenequation, we get
 $$ \begin{align*} &e^{\lambda_0 t}U_t f(x) - (1/\Lambda) \, \phi_0(x) \int_M f(y) \psi_0(y) \,\mu(dy) \\ & = \int_M \left[\left(e^{\lambda_0 (t-2t_0)}u_{t-2t_0}(x,w) - (1/\Lambda) \, \phi_0(x) \psi_0(w)\right) e^{2\lambda_0 t_0} \int_M u_{2t_0}(w,y)f(y) \,\mu(dy)\right]\mu(dw) \\ & = \int_{K_{bt}} \Big( \dots \Big) e^{2\lambda_0 t_0} U_{2t_0} f(w) \,\mu(dw) + \int_{K_{bt}^c} \Big( \dots \Big) e^{2\lambda_0 t_0} U_{2t_0} f(w)\,\mu(dw). \end{align*} $$
$$ \begin{align*} &e^{\lambda_0 t}U_t f(x) - (1/\Lambda) \, \phi_0(x) \int_M f(y) \psi_0(y) \,\mu(dy) \\ & = \int_M \left[\left(e^{\lambda_0 (t-2t_0)}u_{t-2t_0}(x,w) - (1/\Lambda) \, \phi_0(x) \psi_0(w)\right) e^{2\lambda_0 t_0} \int_M u_{2t_0}(w,y)f(y) \,\mu(dy)\right]\mu(dw) \\ & = \int_{K_{bt}} \Big( \dots \Big) e^{2\lambda_0 t_0} U_{2t_0} f(w) \,\mu(dw) + \int_{K_{bt}^c} \Big( \dots \Big) e^{2\lambda_0 t_0} U_{2t_0} f(w)\,\mu(dw). \end{align*} $$
Since
we obtain

where
and
 $$ \begin{gather*} I_2(t,x):= \int_{K_{bt}^c} \left|e^{\lambda_0 (t-2t_0)}u_{t-2t_0}(x,w) - (1/\Lambda) \, \phi_0(x) \psi_0(w)\right| \mu(dw). \end{gather*} $$
$$ \begin{gather*} I_2(t,x):= \int_{K_{bt}^c} \left|e^{\lambda_0 (t-2t_0)}u_{t-2t_0}(x,w) - (1/\Lambda) \, \phi_0(x) \psi_0(w)\right| \mu(dw). \end{gather*} $$
By Lemma 3.3 (with
![]() $s = at$
and
$s = at$
and
![]() $r=bt$
; in particular
$r=bt$
; in particular
![]() $t-2t_0-s-r= bt - 2t_0> 2t_0$
) and pGSD, we see that for all
$t-2t_0-s-r= bt - 2t_0> 2t_0$
) and pGSD, we see that for all
![]() $x \in K_{at}$
,
$x \in K_{at}$
,
Again by pGSD, we get for
![]() $x \in K_{at} \subset K_{t-2t_0}$
,
$x \in K_{at} \subset K_{t-2t_0}$
,
Together this gives, for any measure
![]() $\sigma \in \mathcal {M}^1(K_{at})$
with
$\sigma \in \mathcal {M}^1(K_{at})$
with
![]() $\operatorname {\mathrm {supp}} \sigma \cap (M \setminus \mathcal {N}) \neq \emptyset $
, the estimate
$\operatorname {\mathrm {supp}} \sigma \cap (M \setminus \mathcal {N}) \neq \emptyset $
, the estimate

The estimate for (5.4) follows if we apply the above estimate for
![]() $p=\infty $
to
$p=\infty $
to ![]() ; that is, we get for all
; that is, we get for all
![]() $\sigma \in \mathcal {M}^1(K_{at})$
,
$\sigma \in \mathcal {M}^1(K_{at})$
,
![]() $\operatorname {\mathrm {supp}} \sigma \cap (M \setminus \mathcal {N}) \neq \emptyset $
,
$\operatorname {\mathrm {supp}} \sigma \cap (M \setminus \mathcal {N}) \neq \emptyset $
,

It is important that the constants
![]() $c_3$
and
$c_3$
and
![]() $c_4$
do not depend on
$c_4$
do not depend on
![]() $\sigma $
. Finally, using (5.2), (3.5) and the above estimates, we arrive at
$\sigma $
. Finally, using (5.2), (3.5) and the above estimates, we arrive at

which is valid for all measures
![]() $\sigma \in \mathcal {M}^1(K_{at})$
such that
$\sigma \in \mathcal {M}^1(K_{at})$
such that
![]() $\operatorname {\mathrm {supp}} \sigma \cap (M \setminus \mathcal {N}) \neq \emptyset $
. This completes the proof.
$\operatorname {\mathrm {supp}} \sigma \cap (M \setminus \mathcal {N}) \neq \emptyset $
. This completes the proof.
Remark 5.3. In Theorem 5.2, we prove that pGSD with the exhausting family
![]() $\left \{K_t : t \geqslant t_0\right \}$
implies progressive quasi-ergodicity with
$\left \{K_t : t \geqslant t_0\right \}$
implies progressive quasi-ergodicity with
![]() $\left \{K_{at} : t \geqslant t_0/a\right \}$
, for an arbitrary
$\left \{K_{at} : t \geqslant t_0/a\right \}$
, for an arbitrary
![]() $a \in (0,1)$
. We will see in Section 7.2 that this result is sharp in the sense that one cannot expect progressive quasi-ergodicity which is uniform for the original exhausting family
$a \in (0,1)$
. We will see in Section 7.2 that this result is sharp in the sense that one cannot expect progressive quasi-ergodicity which is uniform for the original exhausting family
![]() $\{K_t : t \geqslant t_0\}$
.
$\{K_t : t \geqslant t_0\}$
.
Our next theorem shows that pGSD is, in fact, equivalent to a version of progressive uniform quasi-ergodicity; cf. Corollary 4.4.
Theorem 5.4. Let M be a locally compact, but not compact, Polish space. Assume that ( A0)–( A4) hold. Then the following conditions are equivalent:
-
a) Both semigroups
 $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
 $\left \{U^*_t: t \geqslant 0 \right \}$
are pGSD.
$\left \{U^*_t: t \geqslant 0 \right \}$
are pGSD. -
b) There exist probability measures
 $\rho , \rho ^* \in \mathcal {M}_1(M)$
such that
$\rho , \rho ^* \in \mathcal {M}_1(M)$
such that
 $\operatorname {\mathrm {supp}} \rho \cap (M \setminus \mathcal {N}) \neq \emptyset $
,
$\operatorname {\mathrm {supp}} \rho \cap (M \setminus \mathcal {N}) \neq \emptyset $
,
 $\operatorname {\mathrm {supp}} \rho ^* \cap (M \setminus \mathcal {N}) \neq \emptyset $
, and an exhausting family of sets
$\operatorname {\mathrm {supp}} \rho ^* \cap (M \setminus \mathcal {N}) \neq \emptyset $
, and an exhausting family of sets
 $\left \{K_t : t \geqslant t_0\right \}$
in M such that and
$\left \{K_t : t \geqslant t_0\right \}$
in M such that and

Proof. The implication ‘a)
![]() $\Rightarrow $
b)’ follows directly from the previous theorem. In order to show the converse direction, we check that the semigroup
$\Rightarrow $
b)’ follows directly from the previous theorem. In order to show the converse direction, we check that the semigroup
![]() $\left \{U_t: t \geqslant 0 \right \}$
is pGSD. The argument for
$\left \{U_t: t \geqslant 0 \right \}$
is pGSD. The argument for
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
is similar.
$\left \{U^*_t: t \geqslant 0 \right \}$
is similar.
Since
![]() $\operatorname {\mathrm {supp}} \rho \cap (M \setminus \mathcal {N}) \neq \emptyset $
, we have
$\operatorname {\mathrm {supp}} \rho \cap (M \setminus \mathcal {N}) \neq \emptyset $
, we have
![]() $\rho (\phi _0)>0$
. Recall that
$\rho (\phi _0)>0$
. Recall that
![]() $\phi _0 \in L^{\infty }(M,\mu )$
. Because of b), there exists some
$\phi _0 \in L^{\infty }(M,\mu )$
. Because of b), there exists some
![]() $t_1>t_0$
such that
$t_1>t_0$
such that

Hence, we have
This gives pGSD for the semigroup
![]() $\left \{U_t: t \geqslant 0 \right \}$
, and the proof is complete.
$\left \{U_t: t \geqslant 0 \right \}$
, and the proof is complete.
We already know that the finiteness of the heat content for large t implies the uniqueness of the quasi-stationary probability measures for both semigroups
![]() $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
; see Theorem 3.4.c). We will now show a much stronger result, which says that the pGSD property and some additional information on the operator norm of
$\left \{U^*_t: t \geqslant 0 \right \}$
; see Theorem 3.4.c). We will now show a much stronger result, which says that the pGSD property and some additional information on the operator norm of
![]() $U_t$
and
$U_t$
and
![]() $U_t^*$
for large times, also imply the uniqueness of the quasi-stationary measures. The additional condition can be expressed as follows: there exists
$U_t^*$
for large times, also imply the uniqueness of the quasi-stationary measures. The additional condition can be expressed as follows: there exists
![]() $t_2>0$
such that
$t_2>0$
such that

Since
(5.5) is equivalent to the combination of the following two conditions (5.6) and (5.7):
 $$ \begin{align} \sup_{t \geqslant t_2} \frac{\left\|U_t\right\|_{\infty,\infty}}{\left\|U_t\right\|_{2,2}} < \infty, \quad \sup_{t \geqslant t_2} \frac{\left\|U^*_t\right\|_{\infty,\infty}}{\left\|U^*_t\right\|_{2,2}} < \infty; \end{align} $$
$$ \begin{align} \sup_{t \geqslant t_2} \frac{\left\|U_t\right\|_{\infty,\infty}}{\left\|U_t\right\|_{2,2}} < \infty, \quad \sup_{t \geqslant t_2} \frac{\left\|U^*_t\right\|_{\infty,\infty}}{\left\|U^*_t\right\|_{2,2}} < \infty; \end{align} $$
If the semigroups
![]() $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
are pGSD for the exhausting family of compact sets
$\left \{U^*_t: t \geqslant 0 \right \}$
are pGSD for the exhausting family of compact sets
![]() $\left \{K_t : t \geqslant t_2\right \}$
, the condition (5.5) is equivalent to
$\left \{K_t : t \geqslant t_2\right \}$
, the condition (5.5) is equivalent to

The next theorem shows that the uniqueness of the quasi-stationary measures extends to a large class of compact semigroups with infinite heat content.
Theorem 5.5. Let M be a locally compact, but not compact, Polish space. Assume that (
A0)–(
A4) hold and that both semigroups
![]() $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
are pGSD and satisfy (5.5). Then the measures m and
$\left \{U^*_t: t \geqslant 0 \right \}$
are pGSD and satisfy (5.5). Then the measures m and
![]() $m^*$
defined in (3.1) are the unique quasi-stationary probability measures of
$m^*$
defined in (3.1) are the unique quasi-stationary probability measures of
![]() $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
, respectively, such that
$\left \{U^*_t: t \geqslant 0 \right \}$
, respectively, such that
![]() $m(M\setminus \mathcal {N})\cdot m^*(M\setminus \mathcal {N})>0$
.
$m(M\setminus \mathcal {N})\cdot m^*(M\setminus \mathcal {N})>0$
.
Proof. We give a proof for the measure m only; the argument for
![]() $m^*$
is similar. Suppose that
$m^*$
is similar. Suppose that
![]() $\bar {m}$
is a quasi-stationary probability measure of
$\bar {m}$
is a quasi-stationary probability measure of
![]() $\left \{U_t: t \geqslant 0 \right \}$
such that
$\left \{U_t: t \geqslant 0 \right \}$
such that
![]() ${\operatorname {\mathrm {supp}} \bar m \cap (M \setminus \mathcal {N}) \neq \emptyset }$
. Following the argument from the proof of Theorem 3.4.c), it is enough to show that
${\operatorname {\mathrm {supp}} \bar m \cap (M \setminus \mathcal {N}) \neq \emptyset }$
. Following the argument from the proof of Theorem 3.4.c), it is enough to show that
![]() $m(f) = \bar {m}(f)$
for
$m(f) = \bar {m}(f)$
for
![]() $f \in L^{\infty }(M,\mu )$
.
$f \in L^{\infty }(M,\mu )$
.
For a compact set
![]() $K \subset M$
such that
$K \subset M$
such that ![]() (in particular,
(in particular,
![]() $\bar {m}(K)> 0$
), we define
$\bar {m}(K)> 0$
), we define

Fix
![]() $f \in L^{\infty }(M,\mu )$
. We have
$f \in L^{\infty }(M,\mu )$
. We have

Using the convergence assertion from Theorem 5.2 with the probability measure
![]() $\sigma = \sigma _K$
, we see that the first term on the right-hand side vanishes as
$\sigma = \sigma _K$
, we see that the first term on the right-hand side vanishes as
![]() $t \to \infty $
. We will now show that for every
$t \to \infty $
. We will now show that for every
![]() $\epsilon \in (0,1)$
, there exists a compact set
$\epsilon \in (0,1)$
, there exists a compact set
![]() $K \subset M$
such that the second term is less than
$K \subset M$
such that the second term is less than
![]() $\epsilon $
, uniformly for large t.
$\epsilon $
, uniformly for large t.
Fix
![]() $\epsilon \in (0,1)$
. By (5.5),
$\epsilon \in (0,1)$
. By (5.5),

Since
![]() $\bar {m}$
is a finite measure, there exists a compact set
$\bar {m}$
is a finite measure, there exists a compact set
![]() $K = K(\epsilon ) \subset M$
as above such that
$K = K(\epsilon ) \subset M$
as above such that
 $$ \begin{align} \bar{m}(K^c) \leqslant \frac{\bar{m}(\phi_0)}{c\left\|\phi_0\right\|_{\infty}(1+\bar{m}(f)+ \left\|f\right\|_{\infty})} \frac{\epsilon}{1+\epsilon}. \end{align} $$
$$ \begin{align} \bar{m}(K^c) \leqslant \frac{\bar{m}(\phi_0)}{c\left\|\phi_0\right\|_{\infty}(1+\bar{m}(f)+ \left\|f\right\|_{\infty})} \frac{\epsilon}{1+\epsilon}. \end{align} $$
The existence of such a set is a consequence of the
![]() $\sigma $
-compactness of the space M. By the quasi-stationarity property of
$\sigma $
-compactness of the space M. By the quasi-stationarity property of
![]() $\bar {m}$
, cf. (3.2), we have
$\bar {m}$
, cf. (3.2), we have
which implies that

From (3.5), we infer that

Combining this inequality with the pGSD property and (5.9) yields

Since the function
![]() $(0,1) \ni x \mapsto x / (1-x)$
is increasing, we finally get
$(0,1) \ni x \mapsto x / (1-x)$
is increasing, we finally get

which completes the proof.
6. Large time asymptotic behavior of compact semigroups
As a by-product of our investigations on quasi-ergodicity, we also obtain some statements on the asymptotic behavior of compact
![]() $L^2$
-semigroups on
$L^2$
-semigroups on
![]() $L^p$
spaces. In this generality, such results seem to be new.
$L^p$
spaces. In this generality, such results seem to be new.
Corollary 6.1. Let M be a locally compact Polish space and assume that (
A0)–(
A3) hold. If there exists some
![]() $t_1 \geqslant t_0$
such that the heat content is finite, that is,
$t_1 \geqslant t_0$
such that the heat content is finite, that is,
then we have the following:
-
a) For every
 $p \in [1,\infty ]$
, there exists
$p \in [1,\infty ]$
, there exists
 $C>0$
such that for every finite measure
$C>0$
such that for every finite measure
 $\sigma $
on M, and for all
$\sigma $
on M, and for all
 $t>6t_1$
and
$t>6t_1$
and
 $t_1 \leqslant s \leqslant t/2$
, we have and
$t_1 \leqslant s \leqslant t/2$
, we have and

In particular, taking
 $\sigma = \delta _z$
,
$\sigma = \delta _z$
,
 $z \in M$
, and
$z \in M$
, and
 $s = t_1$
, we obtain uniform estimates and
$s = t_1$
, we obtain uniform estimates and $$ \begin{gather*} \sup_{x \in M} \sup_{\substack{f \in L^p(M,\mu)\\ \left\|f\right\|_p \leqslant 1}} \left|e^{\lambda_0 t}U_t f(x) - \frac 1\Lambda \, \phi_0(x) \int_M f(y) \psi_0(y) \,\mu(dy)\right| \leqslant \widetilde C \, e^{-\gamma t}, \end{gather*} $$
$$ \begin{gather*} \sup_{x \in M} \sup_{\substack{f \in L^p(M,\mu)\\ \left\|f\right\|_p \leqslant 1}} \left|e^{\lambda_0 t}U_t f(x) - \frac 1\Lambda \, \phi_0(x) \int_M f(y) \psi_0(y) \,\mu(dy)\right| \leqslant \widetilde C \, e^{-\gamma t}, \end{gather*} $$
 $$ \begin{gather*} \sup_{y \in M} \sup_{\substack{f \in L^p(M,\mu)\\ \left\|f\right\|_p \leqslant 1}} \left|e^{\lambda_0 t}U^*_t f(y) - \frac 1\Lambda \, \psi_0(y) \int_M f(x) \phi_0(x) \,\mu(dx)\right| \leqslant \widetilde C \, e^{-\gamma t}. \end{gather*} $$
$$ \begin{gather*} \sup_{y \in M} \sup_{\substack{f \in L^p(M,\mu)\\ \left\|f\right\|_p \leqslant 1}} \left|e^{\lambda_0 t}U^*_t f(y) - \frac 1\Lambda \, \psi_0(y) \int_M f(x) \phi_0(x) \,\mu(dx)\right| \leqslant \widetilde C \, e^{-\gamma t}. \end{gather*} $$
-
b) For every
 $p, r \in [1,\infty ]$
, there exists
$p, r \in [1,\infty ]$
, there exists
 $C>0$
such that for all
$C>0$
such that for all
 $t>6t_1$
, we have and
$t>6t_1$
, we have and $$ \begin{gather*} \sup_{\substack{f \in L^p(M,\mu)\\ \left\|f\right\|_p \leqslant 1}} \left\|e^{\lambda_0 t} U_t f - \frac 1\Lambda \, \phi_0 \int_M f(y) \psi_0(y) \,\mu(dy)\right\|_r \leqslant C \, e^{-\gamma t}, \end{gather*} $$
$$ \begin{gather*} \sup_{\substack{f \in L^p(M,\mu)\\ \left\|f\right\|_p \leqslant 1}} \left\|e^{\lambda_0 t} U_t f - \frac 1\Lambda \, \phi_0 \int_M f(y) \psi_0(y) \,\mu(dy)\right\|_r \leqslant C \, e^{-\gamma t}, \end{gather*} $$
 $$ \begin{gather*} \sup_{\substack{f \in L^p(M,\mu)\\ \left\|f\right\|_p \leqslant 1}} \left\|e^{\lambda_0 t}U^*_t f - \frac 1\Lambda \, \psi_0 \int_M f(x) \phi_0(x) \,\mu(dx)\right\|_r \leqslant C \, e^{-\gamma t}. \end{gather*} $$
$$ \begin{gather*} \sup_{\substack{f \in L^p(M,\mu)\\ \left\|f\right\|_p \leqslant 1}} \left\|e^{\lambda_0 t}U^*_t f - \frac 1\Lambda \, \psi_0 \int_M f(x) \phi_0(x) \,\mu(dx)\right\|_r \leqslant C \, e^{-\gamma t}. \end{gather*} $$
The above bounds follow from direct inspection of the estimates in the proof of Theorem 3.4. The cases
![]() $p=1$
in Part a) and
$p=1$
in Part a) and
![]() $p=1$
,
$p=1$
,
![]() $r=\infty $
in in Part b) are special – they follow directly from (
A2), and the finiteness of the heat content is actually needed in that case.
$r=\infty $
in in Part b) are special – they follow directly from (
A2), and the finiteness of the heat content is actually needed in that case.
Let
![]() $\left \{K_t : t \geqslant t_0\right \}$
be an exhausting family of sets in M. By considering the sequence of measures
$\left \{K_t : t \geqslant t_0\right \}$
be an exhausting family of sets in M. By considering the sequence of measures
![]() $(\sigma _n)$
such that
$(\sigma _n)$
such that
![]() $\sigma _n(\, \cdot \,) := \mu (\, \cdot \, \cap K_n)$
,
$\sigma _n(\, \cdot \,) := \mu (\, \cdot \, \cap K_n)$
,
![]() $n \in \mathbb {N}$
, and using Corollary 6.1.a), we obtain the following asymptotics of the heat content.
$n \in \mathbb {N}$
, and using Corollary 6.1.a), we obtain the following asymptotics of the heat content.
Corollary 6.2. Let M be a locally compact Polish space and assume that (
A0)–(
A3) hold. If there exists some
![]() $t_1 \geqslant t_0$
such that the heat content is finite, that is,
$t_1 \geqslant t_0$
such that the heat content is finite, that is,
then there is some
![]() $C>0$
such that
$C>0$
such that
 $$ \begin{gather*} \left|e^{\lambda_0 t} Z(t) - \frac{\left\|\phi_0\right\|_1 \left\|\psi_0\right\|_1}{\Lambda}\right| \leqslant C e^{-\gamma t}, \quad t> 6t_1. \end{gather*} $$
$$ \begin{gather*} \left|e^{\lambda_0 t} Z(t) - \frac{\left\|\phi_0\right\|_1 \left\|\psi_0\right\|_1}{\Lambda}\right| \leqslant C e^{-\gamma t}, \quad t> 6t_1. \end{gather*} $$
If
![]() $Z(t) = \infty $
for large t’s, we cannot expect the asymptotic estimates to be uniform as in Corollary 6.1.a). Still, we can prove a progressive version which is similar to Theorem 5.2. The following result can be obtained directly by inspection of the proof of that theorem.
$Z(t) = \infty $
for large t’s, we cannot expect the asymptotic estimates to be uniform as in Corollary 6.1.a). Still, we can prove a progressive version which is similar to Theorem 5.2. The following result can be obtained directly by inspection of the proof of that theorem.
Corollary 6.3. Let M be a locally compact, but not compact, Polish space. Assume that (
A0)–(
A4) hold and that both semigroups
![]() $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
![]() $\left \{U^*_t: t \geqslant 0 \right \}$
are pGSD for the exhausting family of compact sets
$\left \{U^*_t: t \geqslant 0 \right \}$
are pGSD for the exhausting family of compact sets
![]() $\left \{K_t : t \geqslant t_0\right \}$
. Then for every
$\left \{K_t : t \geqslant t_0\right \}$
. Then for every
![]() $a, b \in (0,1)$
such that
$a, b \in (0,1)$
such that
![]() $a+2b=1$
and for every
$a+2b=1$
and for every
![]() $p \in [1,\infty ]$
, there exists some
$p \in [1,\infty ]$
, there exists some
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $t>(4/(a \wedge b)) t_0$
,
$t>(4/(a \wedge b)) t_0$
,
 $$ \begin{gather*} \sup_{\sigma \in \mathcal{M}^1(K_{a t})} \sup_{f \in L^p(M,\mu) \atop \left\|f\right\|_p \leqslant 1} \left|e^{\lambda_0 t}\sigma(U_t f) - \frac 1\Lambda \, \sigma(\phi_0) \int_M f(y) \psi_0(y) \,\mu(dy) \right| \leqslant C \kappa_b(t), \end{gather*} $$
$$ \begin{gather*} \sup_{\sigma \in \mathcal{M}^1(K_{a t})} \sup_{f \in L^p(M,\mu) \atop \left\|f\right\|_p \leqslant 1} \left|e^{\lambda_0 t}\sigma(U_t f) - \frac 1\Lambda \, \sigma(\phi_0) \int_M f(y) \psi_0(y) \,\mu(dy) \right| \leqslant C \kappa_b(t), \end{gather*} $$
and
 $$ \begin{gather*} \sup_{\sigma \in \mathcal{M}^1(K_{a t})} \sup_{f \in L^p(M,\mu) \atop \left\|f\right\|_p \leqslant 1} \left|e^{\lambda_0 t}\sigma(U^*_t f) - \frac 1\Lambda \, \sigma(\psi_0) \int_M f(x) \phi_0(x) \,\mu(dx) \right| \leqslant C \kappa_b(t), \end{gather*} $$
$$ \begin{gather*} \sup_{\sigma \in \mathcal{M}^1(K_{a t})} \sup_{f \in L^p(M,\mu) \atop \left\|f\right\|_p \leqslant 1} \left|e^{\lambda_0 t}\sigma(U^*_t f) - \frac 1\Lambda \, \sigma(\psi_0) \int_M f(x) \phi_0(x) \,\mu(dx) \right| \leqslant C \kappa_b(t), \end{gather*} $$
where the time-rate
![]() $\kappa _b(t)$
is given by (5.1). By considering
$\kappa _b(t)$
is given by (5.1). By considering
![]() $\sigma = \delta _z$
,
$\sigma = \delta _z$
,
![]() $z \in K_{a t}$
, we obtain progressive uniform estimate on the sets
$z \in K_{a t}$
, we obtain progressive uniform estimate on the sets
![]() $K_{a t}$
when
$K_{a t}$
when
![]() $t \to \infty $
.
$t \to \infty $
.
7. Examples and applications
7.1. Feynman–Kac semigroups of Feller processes
Suppose that
![]() $(M,d)$
is a locally compact Polish space, and
$(M,d)$
is a locally compact Polish space, and
![]() $\mu $
is a positive, locally finite measure with full topological support on the Borel sets
$\mu $
is a positive, locally finite measure with full topological support on the Borel sets
![]() $\mathcal {B}(M)$
. We assume that the space
$\mathcal {B}(M)$
. We assume that the space
![]() $(M,d)$
is unbounded (in particular, it is not compact) and the measure
$(M,d)$
is unbounded (in particular, it is not compact) and the measure
![]() $\mu $
is not finite. Let
$\mu $
is not finite. Let
![]() $(X_t)_{t \geqslant 0}$
and
$(X_t)_{t \geqslant 0}$
and
![]() $(\widehat {X}_t)_{t \geqslant 0}$
be Markov processes with values in M and the following transition semigroups:
$(\widehat {X}_t)_{t \geqslant 0}$
be Markov processes with values in M and the following transition semigroups:
Throughout this section, we assume that
![]() $P_t$
and
$P_t$
and
![]() $\widehat P_t$
are contractions on
$\widehat P_t$
are contractions on
![]() $L^2(M, \mu )$
and that the semigroups
$L^2(M, \mu )$
and that the semigroups
![]() $\{P_t:t \geqslant 0\}$
,
$\{P_t:t \geqslant 0\}$
,
![]() $\{\widehat P_t :t \geqslant 0\}$
have both the Feller and the strong Feller property (i.e., they are ‘doubly Feller’ in the sense of Chung [Reference Chung11]). Moreover, we assume that the corresponding Markov resolvents are in a weak duality relation with respect to the measure
$\{\widehat P_t :t \geqslant 0\}$
have both the Feller and the strong Feller property (i.e., they are ‘doubly Feller’ in the sense of Chung [Reference Chung11]). Moreover, we assume that the corresponding Markov resolvents are in a weak duality relation with respect to the measure
![]() $\mu $
; see [Reference Chung and Walsh12, Definition 13.1]. By [Reference Chung and Walsh12, Proposition 13.6], we have
$\mu $
; see [Reference Chung and Walsh12, Definition 13.1]. By [Reference Chung and Walsh12, Proposition 13.6], we have
This means that
![]() $\widehat P_t$
is the (functional analytic) adjoint operator
$\widehat P_t$
is the (functional analytic) adjoint operator
![]() $P_t^*$
of
$P_t^*$
of
![]() $P_t$
in the space
$P_t$
in the space
![]() $L^2(M,\mu )$
. Finally, we assume that for every
$L^2(M,\mu )$
. Finally, we assume that for every
![]() $t>0$
, the operators
$t>0$
, the operators
![]() $P_{t}$
and
$P_{t}$
and
![]() $\widehat P_{t}$
are positivity improving and bounded from
$\widehat P_{t}$
are positivity improving and bounded from
![]() $L^2(M,\mu )$
to
$L^2(M,\mu )$
to
![]() $L^{\infty }(M,\mu )$
.
$L^{\infty }(M,\mu )$
.
In particular, the ‘free’ semigropus
![]() $\{P_t, t\geqslant 0\}$
and
$\{P_t, t\geqslant 0\}$
and
![]() $\{\widehat P_t, t\geqslant 0\}$
are such that they satisfy our assumptions (
A1)–(
A3). We are now going to give sufficient criteria such that the corresponding Feynman–Kac semigroups
$\{\widehat P_t, t\geqslant 0\}$
are such that they satisfy our assumptions (
A1)–(
A3). We are now going to give sufficient criteria such that the corresponding Feynman–Kac semigroups
![]() $\{U_t, t\geqslant 0\}$
and
$\{U_t, t\geqslant 0\}$
and
![]() $\{U_t^*, t\geqslant 0\}$
satisfy (
A0)–(
A4).
$\{U_t^*, t\geqslant 0\}$
satisfy (
A0)–(
A4).
Let V be a locally bounded potential on M which is bounded below, that is,
![]() $V = V_{+}-V_{-}$
with
$V = V_{+}-V_{-}$
with
![]() $V_{+} \in L^{\infty }_{\mathrm {loc}}(M,\mu )$
and
$V_{+} \in L^{\infty }_{\mathrm {loc}}(M,\mu )$
and
![]() $V_{-} \in L^{\infty }(M,\mu )$
, for which we define the Feynman–Kac semigroup
$V_{-} \in L^{\infty }(M,\mu )$
, for which we define the Feynman–Kac semigroup
By [Reference Chung and Walsh12, Theorem 13.25], the weak dual or adjoint semigroup consists of operators
We first verify the assumptions (
A1)–(
A3) and show that
![]() $U_t$
and
$U_t$
and
![]() $U^*_t$
are integral operators. If
$U^*_t$
are integral operators. If
![]() $(X_t)_{t\geqslant 0}$
is a stochastic process, we denote by
$(X_t)_{t\geqslant 0}$
is a stochastic process, we denote by
![]() $\tau _B := \inf \left \{t>0 \,:\, X_t\in B^c\right \}$
the first exit time from the set B.
$\tau _B := \inf \left \{t>0 \,:\, X_t\in B^c\right \}$
the first exit time from the set B.
Lemma 7.1. The following assertions hold.
-
a) The operators
 $U_{t}$
,
$U_{t}$
,
 $t>0$
, are positivity improving.
$t>0$
, are positivity improving. -
b) Both semigroups
 $\left \{U_t: t \geqslant 0 \right \}$
and
$\left \{U_t: t \geqslant 0 \right \}$
and
 $\left \{U^*_t: t \geqslant 0 \right \}$
are Feller and strong Feller.
$\left \{U^*_t: t \geqslant 0 \right \}$
are Feller and strong Feller. -
c) For every
 $t>0$
, the operators
$t>0$
, the operators
 $U_t, U^*_t:L^2(M,\mu ) \to L^{\infty }(M,\mu )$
are bounded. In particular, for every
$U_t, U^*_t:L^2(M,\mu ) \to L^{\infty }(M,\mu )$
are bounded. In particular, for every
 $t>0$
, there exists a measurable kernel
$t>0$
, there exists a measurable kernel
 $u_t(x,y)$
such that (2.1) holds, and the semigroups
$u_t(x,y)$
such that (2.1) holds, and the semigroups
 $\{U_t:t\geqslant 0\}$
and
$\{U_t:t\geqslant 0\}$
and
 $\{\widehat U_t:t\geqslant 0\}$
are in duality with respect to the measure
$\{\widehat U_t:t\geqslant 0\}$
are in duality with respect to the measure
 $\mu $
.
$\mu $
.
Proof. a) Let
![]() $0\not \equiv f \in L^2(M,\mu )$
be positive and
$0\not \equiv f \in L^2(M,\mu )$
be positive and
![]() $t, r>0$
. We have
$t, r>0$
. We have
The expectation appearing on the right-hand side tends to
![]() $\mathbb {E}^x f(X_t) = P_tf(x)$
as
$\mathbb {E}^x f(X_t) = P_tf(x)$
as
![]() $r \to \infty $
. Since
$r \to \infty $
. Since
![]() $P_t$
is positivity improving, and V is locally bounded, the expression on the right-hand side is strictly positive for
$P_t$
is positivity improving, and V is locally bounded, the expression on the right-hand side is strictly positive for
![]() $\mu $
-almost every x and sufficiently large
$\mu $
-almost every x and sufficiently large
![]() $r>0$
. To see this, fix any x such that
$r>0$
. To see this, fix any x such that
![]() $P_t f(x)>0$
. Since
$P_t f(x)>0$
. Since
![]() $\mathbb {E}^x \left [f(X_t); t < \tau _{B_r(x)}\right ]$
increases to
$\mathbb {E}^x \left [f(X_t); t < \tau _{B_r(x)}\right ]$
increases to
![]() $P_t f(x) = \mathbb {E}\left [f(X_t)\right ]$
as
$P_t f(x) = \mathbb {E}\left [f(X_t)\right ]$
as
![]() $r\uparrow \infty $
, there is some
$r\uparrow \infty $
, there is some
![]() $r=r(x)$
such that
$r=r(x)$
such that
![]() $\mathbb {E}^x \left [f(X_t); t < \tau _{B_r(x)}\right ]>0$
; hence,
$\mathbb {E}^x \left [f(X_t); t < \tau _{B_r(x)}\right ]>0$
; hence,
![]() $U_t f(x)>0$
. This gives the assertion.
$U_t f(x)>0$
. This gives the assertion.
Part b) follows directly from Chung [Reference Chung11, Theorem 2]. The assumptions (a)–(c) of Chung’s theorem can be easily verified as V is both bounded below and locally bounded.
We still have to prove c). First, observe that for every
![]() $t>0$
, the operators
$t>0$
, the operators
![]() $U_t, U^*_t: L^2(M,\mu ) \to L^{\infty }(M,\mu )$
are bounded. Indeed, for
$U_t, U^*_t: L^2(M,\mu ) \to L^{\infty }(M,\mu )$
are bounded. Indeed, for
![]() $f \in L^2(M,\mu )$
and
$f \in L^2(M,\mu )$
and
![]() $t>0$
, we have
$t>0$
, we have
implying that
![]() $\left \|U_t\right \|_{2,\infty } \leqslant e^{t \left \|V_{-}\right \|_{\infty }} \left \|P_t\right \|_{2,\infty }$
. In the same way, we get
$\left \|U_t\right \|_{2,\infty } \leqslant e^{t \left \|V_{-}\right \|_{\infty }} \left \|P_t\right \|_{2,\infty }$
. In the same way, we get
![]() $\left \|U^*_t\right \|_{2,\infty } \leqslant e^{t \left \|V_{-}\right \|_{\infty }} \left \|P^*_t\right \|_{2,\infty }$
. Combining this with part b) and the semigroup property, we see that for every
$\left \|U^*_t\right \|_{2,\infty } \leqslant e^{t \left \|V_{-}\right \|_{\infty }} \left \|P^*_t\right \|_{2,\infty }$
. Combining this with part b) and the semigroup property, we see that for every
![]() $t>0$
, the operators
$t>0$
, the operators
![]() $U_t, U^*_t$
map
$U_t, U^*_t$
map
![]() $L^2(M,\mu )$
$L^2(M,\mu )$
![]() $\left \{P_t, t\geqslant 0\right \}$
,
$\left \{P_t, t\geqslant 0\right \}$
,
![]() $\left \{\widehat P_t, t\geqslant 0\right \}$
into
$\left \{\widehat P_t, t\geqslant 0\right \}$
into
![]() $L^2(M,\mu ) \cap C_b(M)$
, and we can apply [Reference Jacob and Schilling21, Theorem 1.6] to show that
$L^2(M,\mu ) \cap C_b(M)$
, and we can apply [Reference Jacob and Schilling21, Theorem 1.6] to show that
![]() $U_t, U^*_t$
,
$U_t, U^*_t$
,
![]() $t>0$
, are integral operators. That is, there exist non-negative measurable kernels
$t>0$
, are integral operators. That is, there exist non-negative measurable kernels
![]() $u_t(x,y)$
and
$u_t(x,y)$
and
![]() $u_t^*(x,y)$
such that
$u_t^*(x,y)$
such that
Since the operators
![]() $U_t$
and
$U_t$
and
![]() $U^*_t$
are adjoint, we have
$U^*_t$
are adjoint, we have
![]() $u^*_t(x,y) = u_t(y,x)$
.
$u^*_t(x,y) = u_t(y,x)$
.
Now we give general sufficient conditions for the compactness of the operators
![]() $U_t$
,
$U_t$
,
![]() $U^*_t$
,
$U^*_t$
,
![]() $t>0$
(cf. assumption (
A0)) and for the finiteness of the heat content for large times. Recall that the heat content is defined as
$t>0$
(cf. assumption (
A0)) and for the finiteness of the heat content for large times. Recall that the heat content is defined as
Lemma 7.2. For
![]() $x \in M$
and
$x \in M$
and
![]() $t>0$
, we have
$t>0$
, we have

as well as similar estimates for ![]() . In particular,
. In particular,
for
![]() $t>0$
. Consequently, the following assertions hold.
$t>0$
. Consequently, the following assertions hold.
-
a) If
(7.3)then the operators $$ \begin{align} \lim_{d(x,x_0) \to \infty} V(x) = \infty, \end{align} $$
$$ \begin{align} \lim_{d(x,x_0) \to \infty} V(x) = \infty, \end{align} $$
 $U_t$
,
$U_t$
,
 $U^*_t$
,
$U^*_t$
,
 $t>0$
, are compact; in particular, (
A0) holds.
$t>0$
, are compact; in particular, (
A0) holds.
-
b) Fix
 $t>0$
. Then
$t>0$
. Then  $$ \begin{gather*} \int_{M} e^{-t V(x)}\mu(dx) < \infty \implies Z(t)<\infty. \end{gather*} $$
$$ \begin{gather*} \int_{M} e^{-t V(x)}\mu(dx) < \infty \implies Z(t)<\infty. \end{gather*} $$
However, if
 $\inf _{x \in M} \mathbb {P}^x(t \leqslant \tau _{B_1(x)})>0$
, then
$\inf _{x \in M} \mathbb {P}^x(t \leqslant \tau _{B_1(x)})>0$
, then 
Proof. Fix
![]() $t>0$
. For the proof of the upper bound in (7.1), it is enough to use Jensen’s inequality and Tonelli’s theorem
$t>0$
. For the proof of the upper bound in (7.1), it is enough to use Jensen’s inequality and Tonelli’s theorem

and the upper estimate in (7.2) follows by integration with respect to
![]() $\mu (dx)$
and duality. The lower bounds in (7.1) and (7.2) follow from the definitions. Observe that Part b) follows directly from the latter inequality.
$\mu (dx)$
and duality. The lower bounds in (7.1) and (7.2) follow from the definitions. Observe that Part b) follows directly from the latter inequality.
To get Part a), we show (
A4) for every
![]() $t_0>0$
, and then we use Lemma 2.3. By (7.3), there exists a function
$t_0>0$
, and then we use Lemma 2.3. By (7.3), there exists a function
![]() $g \in C_{\infty }(M)$
such that
$g \in C_{\infty }(M)$
such that
Footnote 2Hence, by (7.1) and (7.4),

By the Feller property, the function
![]() $x \mapsto (1/t)\int _0^t P_s g (x)$
ds belongs to
$x \mapsto (1/t)\int _0^t P_s g (x)$
ds belongs to
![]() $C_{\infty }(M)$
, which implies that (
A4) holds for any
$C_{\infty }(M)$
, which implies that (
A4) holds for any
![]() $t\geqslant t_0$
and any
$t\geqslant t_0$
and any
![]() $t_0>0$
.
$t_0>0$
.
The proof of (
A4) for adjoint operators
![]() $U_t^*$
is similar.
$U_t^*$
is similar.
In particular, Lemma 7.2.b) shows that the finiteness of the heat content is completely independent of the free process.
We will now discuss some concrete classes of Feller processes which are covered by the framework described above. In order to keep the exposition short, we give in each case standard references for the notation and further results.
7.1.1. Lévy processes
Standard references: Sato [Reference Sato49], Jacob [Reference Jacob20, Vol. 1], Schilling [Reference Schilling51]. Throughout this section, the reference measure
![]() $\mu $
is d-dimensional Lebesgue measure and
$\mu $
is d-dimensional Lebesgue measure and
![]() $d(\cdot ,\cdot )$
is the Euclidean distance.
$d(\cdot ,\cdot )$
is the Euclidean distance.
A Lévy process
![]() $(X_t)_{t\geqslant 0}$
is a stochastic process on
$(X_t)_{t\geqslant 0}$
is a stochastic process on
![]() $\mathbb {R}^d$
with càdlàg (right-continuous with finite left limits) paths and stationary and independent increments. A Lévy process can be described in terms of its characteristic exponent
$\mathbb {R}^d$
with càdlàg (right-continuous with finite left limits) paths and stationary and independent increments. A Lévy process can be described in terms of its characteristic exponent
![]() $\psi (\xi ) = -\log \mathbb {E} e^{i\xi \cdot X_1}$
. It is known that
$\psi (\xi ) = -\log \mathbb {E} e^{i\xi \cdot X_1}$
. It is known that
![]() $\psi $
is uniquely determined by the Lévy–Khintchine formula
$\psi $
is uniquely determined by the Lévy–Khintchine formula
 $$ \begin{align} \psi(\xi) = - i \xi \cdot b + \frac 12 \xi \cdot Q \xi + \int_{\mathbb{R}^d \setminus \left\{0\right\}} \left(1 - e^{i \xi \cdot y} + i \xi \cdot y \mathbb{1}_{(0,1)}(|y|)\right)\nu(dy) , \quad \xi \in \mathbb{R}^d, \end{align} $$
$$ \begin{align} \psi(\xi) = - i \xi \cdot b + \frac 12 \xi \cdot Q \xi + \int_{\mathbb{R}^d \setminus \left\{0\right\}} \left(1 - e^{i \xi \cdot y} + i \xi \cdot y \mathbb{1}_{(0,1)}(|y|)\right)\nu(dy) , \quad \xi \in \mathbb{R}^d, \end{align} $$
or by the corresponding the Lévy triplet
![]() $(b,Q,\nu )$
, which is given by
$(b,Q,\nu )$
, which is given by
![]() $b \in \mathbb {R}^d$
(drift term), Q is a symmetric, positive semidefinite
$b \in \mathbb {R}^d$
(drift term), Q is a symmetric, positive semidefinite
![]() $d \times d$
matrix (Gaussian covariance matrix) and
$d \times d$
matrix (Gaussian covariance matrix) and
![]() $\nu $
is a measure on
$\nu $
is a measure on
![]() $\mathbb {R}^d \setminus \left \{0\right \}$
such that
$\mathbb {R}^d \setminus \left \{0\right \}$
such that
![]() $\int _{\mathbb {R}^d \setminus \left \{0\right \}} (1 \wedge |x|^2) \nu (dx) < \infty $
(Lévy measure).
$\int _{\mathbb {R}^d \setminus \left \{0\right \}} (1 \wedge |x|^2) \nu (dx) < \infty $
(Lévy measure).
Lévy processes are Markov processes, which are invariant under translations; that is, the transition semigroup is a convolution semigroup of the form
where
![]() $\widetilde \mu _t(dy) = \mathbb {P}^0(X_t \in -dy)$
is the law of
$\widetilde \mu _t(dy) = \mathbb {P}^0(X_t \in -dy)$
is the law of
![]() $-X_t$
. The dual process
$-X_t$
. The dual process
![]() $(\widehat {X}_t)_{t \geqslant 0}$
of a Lévy process
$(\widehat {X}_t)_{t \geqslant 0}$
of a Lévy process
![]() $(X_t)_{t \geqslant 0}$
is given by
$(X_t)_{t \geqslant 0}$
is given by
![]() $\widehat {X}_t = - X_t$
, and its transition semigroup
$\widehat {X}_t = - X_t$
, and its transition semigroup
![]() $\big \{ \widehat P_t:t \geqslant 0\big \}$
is defined accordingly. The convolution structure of
$\big \{ \widehat P_t:t \geqslant 0\big \}$
is defined accordingly. The convolution structure of
![]() $P_t$
shows that
$P_t$
shows that
![]() $(P_t)_{t\geqslant 0}$
is both a Feller semigroup on
$(P_t)_{t\geqslant 0}$
is both a Feller semigroup on
![]() $C_\infty (\mathbb {R}^d)$
and an
$C_\infty (\mathbb {R}^d)$
and an
![]() $L^p(\mathbb {R}^d,dx)$
Markov semigroup for any
$L^p(\mathbb {R}^d,dx)$
Markov semigroup for any
![]() $p\in [1,\infty )$
.
$p\in [1,\infty )$
.
The process
![]() $(X_t)_{t \geqslant 0}$
is a strong Feller process, that is,
$(X_t)_{t \geqslant 0}$
is a strong Feller process, that is,
![]() $P_t$
maps
$P_t$
maps
![]() $L^{\infty }(\mathbb {R}^d,dx)$
into
$L^{\infty }(\mathbb {R}^d,dx)$
into
![]() $C_b(\mathbb {R}^d)$
, if and only if
$C_b(\mathbb {R}^d)$
, if and only if
![]() $\mu _t(dy) = p_t(y)\,dy$
is absolutely continuous w.r.t. Lebesgue measure; cf. Jacob [Reference Jacob20, Vol. 1, Lemma 4.8.19, 4.8.20]. In particular, the dual process is strong Feller, too. A sufficient condition for the existence of the densities
$\mu _t(dy) = p_t(y)\,dy$
is absolutely continuous w.r.t. Lebesgue measure; cf. Jacob [Reference Jacob20, Vol. 1, Lemma 4.8.19, 4.8.20]. In particular, the dual process is strong Feller, too. A sufficient condition for the existence of the densities
![]() $p_t(x)$
,
$p_t(x)$
,
![]() $t>0$
is that
$t>0$
is that
![]() $Q \neq 0$
or that
$Q \neq 0$
or that
![]() $\nu $
is infinite and absolutely continuous with respect to Lebesgue measure; see, for example, [Reference Sato49, Theorem 27.7], and see also the discussion in [Reference Knopova and Schilling32]. If, in addition, there is some
$\nu $
is infinite and absolutely continuous with respect to Lebesgue measure; see, for example, [Reference Sato49, Theorem 27.7], and see also the discussion in [Reference Knopova and Schilling32]. If, in addition, there is some
![]() $t_0>0$
such that
$t_0>0$
such that
![]() $\int _{\mathbb {R}^d} e^{-t_0 \mathrm {Re} \psi (\xi )}\, d\xi < \infty $
, then
$\int _{\mathbb {R}^d} e^{-t_0 \mathrm {Re} \psi (\xi )}\, d\xi < \infty $
, then
![]() $\sup _{t \geqslant t_0} \sup _{x \in \mathbb {R}^d} p_t(x) < \infty $
, thanks to the Fourier inversion formula. Consequently, the operators
$\sup _{t \geqslant t_0} \sup _{x \in \mathbb {R}^d} p_t(x) < \infty $
, thanks to the Fourier inversion formula. Consequently, the operators
![]() $P_t, \widehat P_t:L^2(\mathbb {R}^d,dx) \to L^{\infty }(\mathbb {R}^d,dx)$
are bounded for every
$P_t, \widehat P_t:L^2(\mathbb {R}^d,dx) \to L^{\infty }(\mathbb {R}^d,dx)$
are bounded for every
![]() $t \geqslant t_0$
. In general, if the integral
$t \geqslant t_0$
. In general, if the integral
![]() $\int _{\mathbb {R}^d} e^{-t_0 \mathrm {Re} \psi (\xi )}\, d\xi $
is finite for every
$\int _{\mathbb {R}^d} e^{-t_0 \mathrm {Re} \psi (\xi )}\, d\xi $
is finite for every
![]() $t_0>0$
, then we get the existence of bounded and jointly (in
$t_0>0$
, then we get the existence of bounded and jointly (in
![]() $(t,x)$
) continuous densities for every
$(t,x)$
) continuous densities for every
![]() $t>0$
; see [Reference Knopova and Schilling32, Lem. 2.1].
$t>0$
; see [Reference Knopova and Schilling32, Lem. 2.1].
In order to see that
![]() $P_t$
and
$P_t$
and
![]() $\widehat P_t$
are positivity improving, it is enough to show that
$\widehat P_t$
are positivity improving, it is enough to show that
![]() $\mathbb {P}^0(X_t \in B) = \mathbb {P}^0(\widehat {X}_t \in -B) = \int _B p_t(x)\,dx>0$
for every Borel set
$\mathbb {P}^0(X_t \in B) = \mathbb {P}^0(\widehat {X}_t \in -B) = \int _B p_t(x)\,dx>0$
for every Borel set
![]() $B \subset \mathbb {R}^d$
with
$B \subset \mathbb {R}^d$
with
![]() $\mathrm {Leb}(B)>0$
. Let us fix such a Borel set B. Using the Lévy–Khintchine formula, we can decompose a Lévy process into a sum of independent Lévy processes
$\mathrm {Leb}(B)>0$
. Let us fix such a Borel set B. Using the Lévy–Khintchine formula, we can decompose a Lévy process into a sum of independent Lévy processes
![]() $X_t = W_t + Y_t$
whose triplets are
$X_t = W_t + Y_t$
whose triplets are
![]() $(b,Q,0)$
and
$(b,Q,0)$
and
![]() $(0,0,\nu )$
. If
$(0,0,\nu )$
. If
![]() $\mathrm {det}(Q)\neq 0$
, then we always have a nondegenerate Gaussian part, and it is clear that
$\mathrm {det}(Q)\neq 0$
, then we always have a nondegenerate Gaussian part, and it is clear that
since
![]() $\mathbb {P}^0(W_t + y \in B)>0$
for all
$\mathbb {P}^0(W_t + y \in B)>0$
for all
![]() $y\in \mathbb {R}^d$
.
$y\in \mathbb {R}^d$
.
Let us assume that
![]() $\mathrm {det}(Q)=0$
. If the Lévy measure
$\mathrm {det}(Q)=0$
. If the Lévy measure
![]() $\nu $
satisfies
$\nu $
satisfies
![]() $\nu (dy) \geqslant h(y)\,dy$
with a density
$\nu (dy) \geqslant h(y)\,dy$
with a density
![]() $h(y)$
which is strictly positive in some neighborhood of
$h(y)$
which is strictly positive in some neighborhood of
![]() $0\in \mathbb {R}^d$
, say
$0\in \mathbb {R}^d$
, say
![]() $B_\epsilon (0)$
, then we can decompose
$B_\epsilon (0)$
, then we can decompose
![]() $X_t = Z_t + C_t$
into two independent Lévy processes whose triplets are
$X_t = Z_t + C_t$
into two independent Lévy processes whose triplets are
![]() $(b,Q,\nu (dy)-h(y)\,dy)$
and
$(b,Q,\nu (dy)-h(y)\,dy)$
and
![]() $(0,0,h(y)\,dy)$
. Since
$(0,0,h(y)\,dy)$
. Since
![]() $C_t$
is a compound Poisson process, we know from [Reference Schilling51, Cor. 3.5] that
$C_t$
is a compound Poisson process, we know from [Reference Schilling51, Cor. 3.5] that
 $$ \begin{gather*} \mathbb{P}^0(C_t \in B) = e^{-h t}\delta_0(B) + e^{-h t} \sum_{k=1}^\infty \frac{t^k}{k!} \int_B h^{*k}(x)\,dx, \quad h = \int_{\mathbb{R}^d} h(x)\,dx. \end{gather*} $$
$$ \begin{gather*} \mathbb{P}^0(C_t \in B) = e^{-h t}\delta_0(B) + e^{-h t} \sum_{k=1}^\infty \frac{t^k}{k!} \int_B h^{*k}(x)\,dx, \quad h = \int_{\mathbb{R}^d} h(x)\,dx. \end{gather*} $$
Since the k-fold convolution
![]() $h^{*k}(x)$
is strictly positive in
$h^{*k}(x)$
is strictly positive in
![]() $B_{\epsilon k}(0)$
, we conclude that
$B_{\epsilon k}(0)$
, we conclude that
![]() ${\mathbb {P}^0(C_t \in B+z)>0}$
for any
${\mathbb {P}^0(C_t \in B+z)>0}$
for any
![]() $z\in \mathbb {R}^d$
; hence,
$z\in \mathbb {R}^d$
; hence,
![]() $\mathbb {P}^0(X_t\in B) = \int \mathbb {P}^0(C_t + z\in B)\,\mathbb {P}^0(Z_t\in dz)>0$
. With a little more effort, the above argument even shows that the density of
$\mathbb {P}^0(X_t\in B) = \int \mathbb {P}^0(C_t + z\in B)\,\mathbb {P}^0(Z_t\in dz)>0$
. With a little more effort, the above argument even shows that the density of
![]() $X_t$
satisfies
$X_t$
satisfies
![]() $p_t(x)>0$
for all
$p_t(x)>0$
for all
![]() $t>0$
and Lebesgue a.a.
$t>0$
and Lebesgue a.a.
![]() $x\in \mathbb {R}^d$
.
$x\in \mathbb {R}^d$
.
It remains to check the conditions for compactness and the finiteness of the heat content stated in Lemma 7.2. Let
![]() $x_0 = 0$
. Choosing the potential V in such a way that
$x_0 = 0$
. Choosing the potential V in such a way that
![]() $V(x) \to \infty $
as
$V(x) \to \infty $
as
![]() $|x| \to \infty $
, we obtain that the Feynman–Kac semigroup operators
$|x| \to \infty $
, we obtain that the Feynman–Kac semigroup operators
![]() $U_t, \widehat U_t$
,
$U_t, \widehat U_t$
,
![]() $t>0$
, are compact operators on
$t>0$
, are compact operators on
![]() $L^2(M,\mu )$
. Moreover, if we know that
$L^2(M,\mu )$
. Moreover, if we know that
 $$ \begin{gather*} \liminf_{|x| \to \infty} \frac{V(x)}{\log|x|}> 0, \end{gather*} $$
$$ \begin{gather*} \liminf_{|x| \to \infty} \frac{V(x)}{\log|x|}> 0, \end{gather*} $$
then there is
![]() $t>0$
such that
$t>0$
such that
![]() $Z(t)<\infty $
.
$Z(t)<\infty $
.
7.1.2. Levy-type processes
Standard references: Jacob [Reference Jacob20, Vol. 1], Böttcher et al. [Reference Böttcher, Schilling and Wang5]. A Lévy-type or Feller process is a Markov process
![]() $X_t$
with values in
$X_t$
with values in
![]() $\mathbb {R}^d$
which behaves locally like a Lévy process. In particular, the transition semigroup
$\mathbb {R}^d$
which behaves locally like a Lévy process. In particular, the transition semigroup
![]() $P_tu(x) = \mathbb {E}^x u(X_t)$
is a Feller semigroup, and one can show that the infinitesimal generator is a pseudo-differential operator of the form
$P_tu(x) = \mathbb {E}^x u(X_t)$
is a Feller semigroup, and one can show that the infinitesimal generator is a pseudo-differential operator of the form
![]() $Au(x) = \mathcal -F^{-1}_{\xi \to x} \left (p(x,\xi )\mathcal Fu(\xi )\right )$
(
$Au(x) = \mathcal -F^{-1}_{\xi \to x} \left (p(x,\xi )\mathcal Fu(\xi )\right )$
(
![]() $\mathcal F$
denotes the Fourier transform, u is a sufficiently regular function – for example, a test function
$\mathcal F$
denotes the Fourier transform, u is a sufficiently regular function – for example, a test function
![]() $u\in C_c^\infty (\mathbb {R}^d)$
) whose symbol
$u\in C_c^\infty (\mathbb {R}^d)$
) whose symbol
![]() $p(x,\xi )$
is, for fixed x, the characteristic exponent of a Lévy process. Therefore,
$p(x,\xi )$
is, for fixed x, the characteristic exponent of a Lévy process. Therefore,
![]() $p(x,\xi )$
is given by a Lévy–Khintchine formula (7.5) where the Lévy-triplet depends on x (i.e.
$p(x,\xi )$
is given by a Lévy–Khintchine formula (7.5) where the Lévy-triplet depends on x (i.e.
![]() $(b,Q,\nu (dy)) = (b(x),Q(x),\nu (x,dy))$
). Thus, A is a ‘Lévy generator with variable coefficients’. A typical example are stable-like generators of the form
$(b,Q,\nu (dy)) = (b(x),Q(x),\nu (x,dy))$
). Thus, A is a ‘Lévy generator with variable coefficients’. A typical example are stable-like generators of the form
![]() $Au(x) = (-\Delta )^{\alpha (x)}u(x)$
where
$Au(x) = (-\Delta )^{\alpha (x)}u(x)$
where
![]() $\alpha :\mathbb {R}^d \to [0,2]$
is a variable order of differentiability and the symbol is of the form
$\alpha :\mathbb {R}^d \to [0,2]$
is a variable order of differentiability and the symbol is of the form
![]() $p(x,\xi ) = |\xi |^{\alpha (x)}$
$p(x,\xi ) = |\xi |^{\alpha (x)}$
It is a major problem to construct a Lévy-type process given an admissible symbol
![]() $p(x,\xi )$
or, which is the same, an x-dependent Lévy triplet. A thorough discussion is in Jacob [Reference Jacob20, Vol. 3] and Böttcher et al. [Reference Böttcher, Schilling and Wang5]; probably the most general results to-date are due to Kühn [Reference Kühn34] and Knopova et al. [Reference Knopova, Kulik and Schilling33].
$p(x,\xi )$
or, which is the same, an x-dependent Lévy triplet. A thorough discussion is in Jacob [Reference Jacob20, Vol. 3] and Böttcher et al. [Reference Böttcher, Schilling and Wang5]; probably the most general results to-date are due to Kühn [Reference Kühn34] and Knopova et al. [Reference Knopova, Kulik and Schilling33].
In what follows, we indicate some conditions, under which the assumptions needed in Section 7.1 are satisfied. Our main intention is not to cover the most general situation, but to illustrate that within the class of Lévy-type processes, there are many examples to be found. The following assumptions on the symbol are frequently used:
where
![]() $C_1,C_2,C_3$
are constants and
$C_1,C_2,C_3$
are constants and
![]() $\alpha _0,\alpha ,\beta \in (0,2]$
and
$\alpha _0,\alpha ,\beta \in (0,2]$
and
![]() $\gamma \in (0,\beta )$
are suitable exponents.
$\gamma \in (0,\beta )$
are suitable exponents.
Assume that
![]() $p(x,\xi )$
is the symbol of a Lévy-type process. If either
$p(x,\xi )$
is the symbol of a Lévy-type process. If either
![]() ${\alpha \kern1.3pt{\geqslant}\kern1.3pt \gamma\kern1.3pt{>}\kern1.3pt \frac {\alpha }{\alpha _0}\left (\alpha \kern1.3pt{-}\kern1.3pt\alpha _0\kern1.3pt{+}\kern1.3pt\frac 12\right )}$
or
${\alpha \kern1.3pt{\geqslant}\kern1.3pt \gamma\kern1.3pt{>}\kern1.3pt \frac {\alpha }{\alpha _0}\left (\alpha \kern1.3pt{-}\kern1.3pt\alpha _0\kern1.3pt{+}\kern1.3pt\frac 12\right )}$
or
![]() $\alpha \leqslant \gamma < \frac 2\alpha _0-\frac 12$
, then
$\alpha \leqslant \gamma < \frac 2\alpha _0-\frac 12$
, then
![]() $X_t$
has a transition density
$X_t$
has a transition density
![]() $p_t(x,y)$
such that
$p_t(x,y)$
such that
![]() $\sup _x \int p_t^2(x,y)\,dy<\infty $
(i.e., (
A3) holds for the free semigroup
$\sup _x \int p_t^2(x,y)\,dy<\infty $
(i.e., (
A3) holds for the free semigroup
![]() $P_t$
; see [Reference Kühn34, Thm. 2.14]).
$P_t$
; see [Reference Kühn34, Thm. 2.14]).
The existence of a Lévy-type process with a given symbol
![]() $p(x,\xi )$
is a much more delicate issue. Here, we content ourselves to mentioning that in the stable-like case
$p(x,\xi )$
is a much more delicate issue. Here, we content ourselves to mentioning that in the stable-like case
![]() $p(x,\xi ) = |\xi |^{\alpha (x)}$
where
$p(x,\xi ) = |\xi |^{\alpha (x)}$
where
![]() $\alpha : \mathbb {R}^d \to [a_1,a_2] \subset (0,2)$
is Hölder continuous, the existence of a stable-like process with a continuous density
$\alpha : \mathbb {R}^d \to [a_1,a_2] \subset (0,2)$
is Hölder continuous, the existence of a stable-like process with a continuous density
![]() $(t,x,y)\mapsto p_t(x,y)> 0$
has been established in [Reference Kühn34, Thm. 3.8, Thm. 3.11] as well as in [Reference Knopova, Kulik and Schilling33, Section 3]. In particular, we get Feller and strong Feller processes. It is also clear that stable-like symbols satisfy the assumptions (7.6)–(7.8). We would like to mention that the methods presented in these papers go way beyond the stable-like case; [Reference Kühn34] covers symbols of the type
$(t,x,y)\mapsto p_t(x,y)> 0$
has been established in [Reference Kühn34, Thm. 3.8, Thm. 3.11] as well as in [Reference Knopova, Kulik and Schilling33, Section 3]. In particular, we get Feller and strong Feller processes. It is also clear that stable-like symbols satisfy the assumptions (7.6)–(7.8). We would like to mention that the methods presented in these papers go way beyond the stable-like case; [Reference Kühn34] covers symbols of the type
![]() $p(x,\xi ) = \psi _{a(x)}(|\xi |)$
where
$p(x,\xi ) = \psi _{a(x)}(|\xi |)$
where
![]() $z\mapsto \psi _a(z)$
has a holomorphic extension on a bow-tie shaped domain of the complex plane (and satisfies certain polynomial boundedness assumptions), while [Reference Knopova, Kulik and Schilling33] are mainly interested in non-rotationally symmetric symbols. Therefore, (
A1) and (
A2) are also satisfied.
$z\mapsto \psi _a(z)$
has a holomorphic extension on a bow-tie shaped domain of the complex plane (and satisfies certain polynomial boundedness assumptions), while [Reference Knopova, Kulik and Schilling33] are mainly interested in non-rotationally symmetric symbols. Therefore, (
A1) and (
A2) are also satisfied.
In general, it is very difficult to determine the symbol of the (formal) adjoint to A. Building on [Reference Schilling and Uemura53], the paper [Reference Schilling and Wang54] contains the general form of the symbol of the adjoint operator for a wide class of symbols (Section 3) and a fully-worked out discussion of the case
![]() $p(x,\xi )=|\xi |^{\alpha (x)}$
. If
$p(x,\xi )=|\xi |^{\alpha (x)}$
. If
![]() $\alpha (x)$
is Hölder, takes values in
$\alpha (x)$
is Hölder, takes values in
![]() ${[a_1,a_2]\subset (0,2)}$
and satisfies (7.6)–(7.8), then so does the adjoint symbol
${[a_1,a_2]\subset (0,2)}$
and satisfies (7.6)–(7.8), then so does the adjoint symbol
![]() $p^*(x,\xi )$
which is given by a Lévy–Khintchine formula with triplet
$p^*(x,\xi )$
which is given by a Lévy–Khintchine formula with triplet
![]() $(0,0,w(x)|x-y|^{-d-\alpha (x)}\,dy)$
for the weight
$(0,0,w(x)|x-y|^{-d-\alpha (x)}\,dy)$
for the weight
![]() ${w(x) = \alpha (x)2^{\alpha (x)-1}\Gamma \left (\frac 12\alpha (x)+\frac 12d\right )\big /\Gamma \left (1-\frac 12\alpha (x)\right )}$
. This means that the assumptions (
A1)–(
A3) also hold for the adjoint free semigroup
${w(x) = \alpha (x)2^{\alpha (x)-1}\Gamma \left (\frac 12\alpha (x)+\frac 12d\right )\big /\Gamma \left (1-\frac 12\alpha (x)\right )}$
. This means that the assumptions (
A1)–(
A3) also hold for the adjoint free semigroup
![]() $\widehat P_t$
in this case. Of course, other symbols require case-by-case investigations (e.g., based on the above-mentioned literature).
$\widehat P_t$
in this case. Of course, other symbols require case-by-case investigations (e.g., based on the above-mentioned literature).
7.1.3. Continuous-time Markov chains on a countably infinite uniformly discrete metric space
Standard references: Murugan and Saloff–Coste [Reference Murugan and Saloff-Coste46, Reference Murugan and Saloff-Coste47] and Cygan, Kaleta and Sliwiński [Reference Cygan, Kaleta and Śliwiński14]. Let
![]() $(M,d)$
be a countably infinite, unbounded, complete metric space, which is also uniformly discrete; this means that there exists a number
$(M,d)$
be a countably infinite, unbounded, complete metric space, which is also uniformly discrete; this means that there exists a number
![]() $a>0$
such for any two distinct points
$a>0$
such for any two distinct points
![]() $x,y \in M$
, one has
$x,y \in M$
, one has
![]() $d(x,y) \geqslant a$
; see [Reference Murugan and Saloff-Coste46, Reference Murugan and Saloff-Coste47]. The underlying measure
$d(x,y) \geqslant a$
; see [Reference Murugan and Saloff-Coste46, Reference Murugan and Saloff-Coste47]. The underlying measure
![]() $\mu :M \to (0,\infty )$
is assumed to be a Frostman measure with exponent
$\mu :M \to (0,\infty )$
is assumed to be a Frostman measure with exponent
![]() $d_M>0$
(i.e., there is a constant
$d_M>0$
(i.e., there is a constant
![]() $c>0$
such that
$c>0$
such that
![]() $\mu (B_r(x)) \leqslant c r^{d_M}$
for any
$\mu (B_r(x)) \leqslant c r^{d_M}$
for any
![]() $x \in M$
and
$x \in M$
and
![]() $r>0$
).
$r>0$
).
In particular, we have for all
![]() $\gamma>d_M$
,
$\gamma>d_M$
,
 $$ \begin{align*} \int_{B_1(x_0)^c} d(x,x_0)^{-\gamma}\, \mu(dx) & = \sum_{n=0}^{\infty} \int_{2^n \leqslant d(x,x_0) < 2^{n+1}} d(x,x_0)^{-\gamma}\, \mu(dx) \\ & \leqslant \sum_{n=0}^{\infty} 2^{-\gamma n} \mu(B_{2^{n+1}}(x_0)) \leqslant c 2^{d_M}\sum_{n=0}^{\infty} 2^{-(\gamma-d_M) n} < \infty. \end{align*} $$
$$ \begin{align*} \int_{B_1(x_0)^c} d(x,x_0)^{-\gamma}\, \mu(dx) & = \sum_{n=0}^{\infty} \int_{2^n \leqslant d(x,x_0) < 2^{n+1}} d(x,x_0)^{-\gamma}\, \mu(dx) \\ & \leqslant \sum_{n=0}^{\infty} 2^{-\gamma n} \mu(B_{2^{n+1}}(x_0)) \leqslant c 2^{d_M}\sum_{n=0}^{\infty} 2^{-(\gamma-d_M) n} < \infty. \end{align*} $$
Under these assumptions, we can give a sufficient condition for the integrability of the function
![]() $x \mapsto e^{-tV(x)}$
which is needed for the finiteness of the heat content; see Lemma 7.2.b). Indeed, if there exist
$x \mapsto e^{-tV(x)}$
which is needed for the finiteness of the heat content; see Lemma 7.2.b). Indeed, if there exist
![]() $c_0, R>0$
and
$c_0, R>0$
and
![]() $x_0 \in M$
such that
$x_0 \in M$
such that
 $$ \begin{gather*} \frac{V(x)}{\log d(x,x_0)} \geqslant c_0>0 , \quad d(x,x_0) \geqslant R, \end{gather*} $$
$$ \begin{gather*} \frac{V(x)}{\log d(x,x_0)} \geqslant c_0>0 , \quad d(x,x_0) \geqslant R, \end{gather*} $$
then for every
![]() $t> d_M/c_0$
, we have
$t> d_M/c_0$
, we have
 $$ \begin{gather*} \int_M e^{-tV(x)} \mu(dx) \leqslant e^{\left\|V_-\right\|_{\infty}} \mu(B_R(x_0)) + \int_{B_R(x_0)^c} d(x,x_0)^{-c_0t} \mu(dx) < \infty. \end{gather*} $$
$$ \begin{gather*} \int_M e^{-tV(x)} \mu(dx) \leqslant e^{\left\|V_-\right\|_{\infty}} \mu(B_R(x_0)) + \int_{B_R(x_0)^c} d(x,x_0)^{-c_0t} \mu(dx) < \infty. \end{gather*} $$
Consider two probability kernels
![]() $Q, \widehat Q:M \times M \to [0,1]$
,
$Q, \widehat Q:M \times M \to [0,1]$
,
![]() $\sum _{y \in M} Q(x,y) = 1=\sum _{y \in M} \widehat Q(x,y)$
,
$\sum _{y \in M} Q(x,y) = 1=\sum _{y \in M} \widehat Q(x,y)$
,
![]() $x \in M$
, which are connected via the duality relation with respect to the measure
$x \in M$
, which are connected via the duality relation with respect to the measure
![]() $\mu $
– that is,
$\mu $
– that is,
Thus, there are two time-homogeneous Markov chains
![]() $\{Z_n: n \in \mathbb {N}_0\}$
,
$\{Z_n: n \in \mathbb {N}_0\}$
,
![]() $\{\widehat Z_n: n \in \mathbb {N}_0\}$
with values in M and one-step transition probabilities given by Q and
$\{\widehat Z_n: n \in \mathbb {N}_0\}$
with values in M and one-step transition probabilities given by Q and
![]() $\widehat Q$
, respectively. We denote by
$\widehat Q$
, respectively. We denote by
![]() $\mathbb {P}^x$
,
$\mathbb {P}^x$
,
![]() $\widehat {\mathbb {P}}^x$
the laws of the chains starting at
$\widehat {\mathbb {P}}^x$
the laws of the chains starting at
![]() $x \in M$
– that is,
$x \in M$
– that is,
We have
where ![]() ,
,
![]() $Q_1(x,y)=Q(x,y)$
and
$Q_1(x,y)=Q(x,y)$
and
![]() ${Q_{n+1}(x,y) = \sum _{z \in M} Q_n(x,z)Q_1(z,y)}$
,
${Q_{n+1}(x,y) = \sum _{z \in M} Q_n(x,z)Q_1(z,y)}$
,
![]() ${n \geqslant 1}$
, and
${n \geqslant 1}$
, and
![]() $\widehat Q_n$
’s are defined accordingly. The densities with respect to
$\widehat Q_n$
’s are defined accordingly. The densities with respect to
![]() $\mu $
are given by
$\mu $
are given by
 $$ \begin{gather*} q_n(x,y) = \frac{\mathbb{P}^x (Z_{n}=y)}{\mu(y)} = \frac{Q_n(x,y)}{\mu(y)} \quad \text{and} \quad \widehat q_n(x,y) = \frac{\widehat{\mathbb{P}}^x (\widehat Z_{n}=y)}{\mu(y)} = \frac{\widehat Q_n(x,y)}{\mu(y)}. \end{gather*} $$
$$ \begin{gather*} q_n(x,y) = \frac{\mathbb{P}^x (Z_{n}=y)}{\mu(y)} = \frac{Q_n(x,y)}{\mu(y)} \quad \text{and} \quad \widehat q_n(x,y) = \frac{\widehat{\mathbb{P}}^x (\widehat Z_{n}=y)}{\mu(y)} = \frac{\widehat Q_n(x,y)}{\mu(y)}. \end{gather*} $$
Clearly, (7.9) extends to
![]() $\mu (x) Q_n(x,y) = \mu (y) \widehat Q_n(y,x)$
,
$\mu (x) Q_n(x,y) = \mu (y) \widehat Q_n(y,x)$
,
![]() $x,y \in M$
,
$x,y \in M$
,
![]() $n \in \mathbb {N}$
, and we have
$n \in \mathbb {N}$
, and we have
![]() $\widehat q_n(x,y) = q_n(y,x)$
. The corresponding n-step transition operator is
$\widehat q_n(x,y) = q_n(y,x)$
. The corresponding n-step transition operator is
whenever the series is finite;
![]() $\widehat Q_n f$
is defined in a similar way.
$\widehat Q_n f$
is defined in a similar way.
The main objects are the continuous-time chains
![]() $\{X_t: t \geqslant 0\}$
and
$\{X_t: t \geqslant 0\}$
and
![]() $\{\widehat X_t: t \geqslant 0\}$
defined by
$\{\widehat X_t: t \geqslant 0\}$
defined by
![]() $X_t:= Z_{N_t}$
,
$X_t:= Z_{N_t}$
,
![]() $\widehat X_t:= \widehat Z_{N_t}$
, respectively, where
$\widehat X_t:= \widehat Z_{N_t}$
, respectively, where
![]() $\{N_t: t \geqslant 0\}$
is an independent Poisson process with parameter
$\{N_t: t \geqslant 0\}$
is an independent Poisson process with parameter
![]() $\lambda =1$
. Clearly, we have
$\lambda =1$
. Clearly, we have
![]() $\mathbb {P}^x(X_t \in A) = \sum _{y \in A} P_t(x,y)$
,
$\mathbb {P}^x(X_t \in A) = \sum _{y \in A} P_t(x,y)$
,
![]() $A \subset M$
, where
$A \subset M$
, where
 $$ \begin{gather*} P_t(x,y) = e^{-t}\sum_{n=0}^{\infty} \frac{t^n}{n!} Q_{n}(x,y), \quad t>0, \ x \in M. \end{gather*} $$
$$ \begin{gather*} P_t(x,y) = e^{-t}\sum_{n=0}^{\infty} \frac{t^n}{n!} Q_{n}(x,y), \quad t>0, \ x \in M. \end{gather*} $$
The transition semigroup
![]() $\{P_t: t \geqslant 0\}$
of this process is defined as
$\{P_t: t \geqslant 0\}$
of this process is defined as
 $$ \begin{gather*} P_t f(x) = \sum_{y \in M} f(y) P_t(x,y) = \sum_{y \in M} f(y) p_t(x,y) \mu(y), \quad \text{with} \quad p_t(x,y):=\frac{P_t(x,y)}{\mu(y)}, \end{gather*} $$
$$ \begin{gather*} P_t f(x) = \sum_{y \in M} f(y) P_t(x,y) = \sum_{y \in M} f(y) p_t(x,y) \mu(y), \quad \text{with} \quad p_t(x,y):=\frac{P_t(x,y)}{\mu(y)}, \end{gather*} $$
for all admissible functions f on M. The transition probabilities
![]() $\widehat P_t(x,y)$
, kernels
$\widehat P_t(x,y)$
, kernels
![]() $\widehat p_t(x,y)$
and the transition semigroup
$\widehat p_t(x,y)$
and the transition semigroup
![]() $\{\widehat P_t: t \geqslant 0\}$
of the process
$\{\widehat P_t: t \geqslant 0\}$
of the process
![]() $\{\widehat {X}_t: t \geqslant 0\}$
are defined accordingly. By the Cauchy–Schwarz inequality, we can easily see that all operators
$\{\widehat {X}_t: t \geqslant 0\}$
are defined accordingly. By the Cauchy–Schwarz inequality, we can easily see that all operators
![]() $P_t$
and
$P_t$
and
![]() $\widehat {P}_t$
are contractions on
$\widehat {P}_t$
are contractions on
![]() $L^2(M,\mu )$
; again, we have
$L^2(M,\mu )$
; again, we have
![]() $\widehat p_t(x,y) = p_t(y,x)$
, which means that the weak duality relation, which was described at the beginning of Section 7.1, is in force. Moreover, it is straightforward to see that both transition semigroups are doubly Feller. In particular, the strong Feller property follows from the fact that
$\widehat p_t(x,y) = p_t(y,x)$
, which means that the weak duality relation, which was described at the beginning of Section 7.1, is in force. Moreover, it is straightforward to see that both transition semigroups are doubly Feller. In particular, the strong Feller property follows from the fact that
![]() $(M,d)$
is uniformly discrete. One can also check that the ultracontractivity of these semigroups is equivalent to the boundedness of the kernel
$(M,d)$
is uniformly discrete. One can also check that the ultracontractivity of these semigroups is equivalent to the boundedness of the kernel
![]() $q_1(x,y)$
(e.g., if
$q_1(x,y)$
(e.g., if
![]() $\inf _{x \in M} \mu (x)>0$
). The positivity improving property follows from the strict positivity of the kernels
$\inf _{x \in M} \mu (x)>0$
). The positivity improving property follows from the strict positivity of the kernels
![]() $P_t(x,y)$
and
$P_t(x,y)$
and
![]() $\widehat P_t(x,y)$
. This is the case if the chains
$\widehat P_t(x,y)$
. This is the case if the chains
![]() $\{Z_n: n \in \mathbb {N}_0\}$
,
$\{Z_n: n \in \mathbb {N}_0\}$
,
![]() $\{\widehat Z_n: n \in \mathbb {N}_0\}$
are irreducible (i.e., for every
$\{\widehat Z_n: n \in \mathbb {N}_0\}$
are irreducible (i.e., for every
![]() $x,y \in M$
, there is
$x,y \in M$
, there is
![]() $n=n(x,y) \in \mathbb {N}$
such that
$n=n(x,y) \in \mathbb {N}$
such that
![]() $P_n(x,y), \widehat P_n(x,y)>0$
).
$P_n(x,y), \widehat P_n(x,y)>0$
).
We can now explicitly estimate the space-rates of the quasi-ergodic behavior of the Feynman–Kac semigroups with confining potentials (see Corollary 3.5). These rates take the form ![]() and
and ![]() , for some
, for some
![]() $t_1>0$
. The functions
$t_1>0$
. The functions ![]() and
and ![]() can be estimated by a constant or by using the upper bound in (7.1). Sharper estimates for a large class of processes will be provided in [Reference Cygan, Kaleta, Schilling and Śliwiński13]. However, sharp lower estimates for the ground states for a fairly general class of processes and rather general confining potentials can be found in [Reference Cygan, Kaleta and Śliwiński14].
can be estimated by a constant or by using the upper bound in (7.1). Sharper estimates for a large class of processes will be provided in [Reference Cygan, Kaleta, Schilling and Śliwiński13]. However, sharp lower estimates for the ground states for a fairly general class of processes and rather general confining potentials can be found in [Reference Cygan, Kaleta and Śliwiński14].
If we have good lower estimates for the ground states, then we can apply Lemma 4.5 and Theorem 4.6 to derive the progressive GSD and progressive exponential quasi-ergodicity from the finiteness of the heat content for large times. Such estimates can, for example, be found in [Reference Cygan, Kaleta and Śliwiński14].
7.1.4. Continuous-time simple random walk on an infinite graph
Standard reference: Barlow [Reference Barlow4]. This is a special case of the example in the previous section: Let M be a countably infinite set and
![]() $\Gamma =(M,E)$
be a connected and locally finite graph over M. We equip M with its geodesic metric
$\Gamma =(M,E)$
be a connected and locally finite graph over M. We equip M with its geodesic metric
![]() $d: M \times M \to \mathbb {N}_0$
; the underlying measure and the transition probability of a simple random walk on the graph is defined in terms of a conductance network on
$d: M \times M \to \mathbb {N}_0$
; the underlying measure and the transition probability of a simple random walk on the graph is defined in terms of a conductance network on
![]() $\Gamma $
. The Frostman property of the measure
$\Gamma $
. The Frostman property of the measure
![]() $\mu = (\mu _x)_{x\in M}$
is, for example, guaranteed by the following condition: there is a constant
$\mu = (\mu _x)_{x\in M}$
is, for example, guaranteed by the following condition: there is a constant
![]() $c_1>0$
such that
$c_1>0$
such that
![]() $\mu _x \leqslant c_1$
,
$\mu _x \leqslant c_1$
,
![]() $x \in M$
, and the cardinality of a geodesic ball
$x \in M$
, and the cardinality of a geodesic ball
![]() $B_n(x)$
is controlled by a power-type function (i.e.,
$B_n(x)$
is controlled by a power-type function (i.e.,
![]() $\sup _{x\in M} \sup _{n\in \mathbb {N}} n^{-d_M}|B_n(x)| <\infty $
for some
$\sup _{x\in M} \sup _{n\in \mathbb {N}} n^{-d_M}|B_n(x)| <\infty $
for some
![]() $d_M>0$
).
$d_M>0$
).
7.1.5. Brownian motion on simple nested fractals
Standard references: Lindstrøm [Reference Lindstrøm41], Kusuoka [Reference Kusuoka37], Fukushima [Reference Fukushima19], Kumagai [Reference Kumagai35]. Let
![]() $M \subset \mathbb {R}^d$
,
$M \subset \mathbb {R}^d$
,
![]() $d \geqslant 1$
, be an (unbounded) simple nested fractal and let
$d \geqslant 1$
, be an (unbounded) simple nested fractal and let
![]() $(X_t)_{t \geqslant 0}$
be a Brownian motion with the state space M. We refer the reader to [Reference Lindstrøm41, Reference Kusuoka37, Reference Fukushima19] for the definition of a simple nested fractal and various constructions of Brownian motion thereon. The set M inherits the Euclidean topology from
$(X_t)_{t \geqslant 0}$
be a Brownian motion with the state space M. We refer the reader to [Reference Lindstrøm41, Reference Kusuoka37, Reference Fukushima19] for the definition of a simple nested fractal and various constructions of Brownian motion thereon. The set M inherits the Euclidean topology from
![]() $\mathbb {R}^d$
, and the measure
$\mathbb {R}^d$
, and the measure
![]() $\mu $
is the Hausdorff measure on M (in particular,
$\mu $
is the Hausdorff measure on M (in particular,
![]() $\mu $
is a
$\mu $
is a
![]() $d_M$
-Frostman measure, where
$d_M$
-Frostman measure, where
![]() $d_M$
is the Hausdorff dimension of M). It is known that
$d_M$
is the Hausdorff dimension of M). It is known that
![]() $(X_t)_{t \geqslant 0}$
is a Markov process with symmetric, jointly continuous and bounded transition densities that satisfy sub-Gaussian estimates [Reference Kumagai35, Section 5]. Consequently, the transition semigroup of the process
$(X_t)_{t \geqslant 0}$
is a Markov process with symmetric, jointly continuous and bounded transition densities that satisfy sub-Gaussian estimates [Reference Kumagai35, Section 5]. Consequently, the transition semigroup of the process
![]() $(X_t)_{t \geqslant 0}$
is a doubly Feller, ultracontractive and positivity improving semigroup.
$(X_t)_{t \geqslant 0}$
is a doubly Feller, ultracontractive and positivity improving semigroup.
7.1.6. Sobordinate processes
Standard references: Sato [Reference Sato49], Schilling, Song and Vondraček [Reference Schilling, Song and Vondraček52]. Another class of processes which is covered by our results are subordinate processes. Recall that a subordinator is an increasing Lévy process with values in
![]() $[0,\infty )$
, starting at
$[0,\infty )$
, starting at
![]() $0$
. It is uniquely determined by its Laplace transform: we have
$0$
. It is uniquely determined by its Laplace transform: we have
![]() $\mathbb {E} e^{-\lambda S_t} = e^{- t \phi (\lambda )}$
,
$\mathbb {E} e^{-\lambda S_t} = e^{- t \phi (\lambda )}$
,
![]() $t>0$
, where the exponent
$t>0$
, where the exponent
![]() $\phi :(0,\infty ) \to [0,\infty )$
is a Bernstein function of the form
$\phi :(0,\infty ) \to [0,\infty )$
is a Bernstein function of the form
 $$ \begin{gather*} \phi(\lambda) = b \lambda + \int_0^{\infty} (1- e^{-\lambda u}) \,\rho(du). \end{gather*} $$
$$ \begin{gather*} \phi(\lambda) = b \lambda + \int_0^{\infty} (1- e^{-\lambda u}) \,\rho(du). \end{gather*} $$
Here,
![]() $b \geqslant 0$
is the drift term and
$b \geqslant 0$
is the drift term and
![]() $\rho $
is a measure on
$\rho $
is a measure on
![]() $(0,\infty )$
such that
$(0,\infty )$
such that
![]() $\int _0^{\infty } (1 \wedge u) \rho (du) < \infty $
(Lévy measure).
$\int _0^{\infty } (1 \wedge u) \rho (du) < \infty $
(Lévy measure).
Let
![]() $\{X_t: t \geqslant 0\}$
and
$\{X_t: t \geqslant 0\}$
and
![]() $\{\widehat X_t: t \geqslant 0\}$
be Markov processes as in Section 7.1, and let
$\{\widehat X_t: t \geqslant 0\}$
be Markov processes as in Section 7.1, and let
![]() $\{S_t: t \geqslant 0\}$
be a subordinator which is independent of
$\{S_t: t \geqslant 0\}$
be a subordinator which is independent of
![]() $\{X_t: t \geqslant 0\}$
and
$\{X_t: t \geqslant 0\}$
and
![]() $\{\widehat X_t: t \geqslant 0\}$
. We define the subordinate processes
$\{\widehat X_t: t \geqslant 0\}$
. We define the subordinate processes
![]() $\{X^{\phi }_t: t \geqslant 0\}$
,
$\{X^{\phi }_t: t \geqslant 0\}$
,
![]() $\{\widehat X^{\phi }_t: t \geqslant 0\}$
by the formulas
$\{\widehat X^{\phi }_t: t \geqslant 0\}$
by the formulas
![]() $X^{\phi }_t:= X_{S_t}$
,
$X^{\phi }_t:= X_{S_t}$
,
![]() $\widehat X^{\phi }_t:= \widehat X_{S_t}$
, respectively. By independence, their transition semigroups
$\widehat X^{\phi }_t:= \widehat X_{S_t}$
, respectively. By independence, their transition semigroups
![]() $\{P^{\phi }_t: t \geqslant 0\}$
and
$\{P^{\phi }_t: t \geqslant 0\}$
and
![]() $\{\widehat P^{\phi }_t: t \geqslant 0\}$
are given by
$\{\widehat P^{\phi }_t: t \geqslant 0\}$
are given by
 $$ \begin{gather*} P^{\phi}_t f(x) = \int_{[0,\infty)} P_s f(x) \,\mathbb{P}(S_t \in ds), \quad \widehat P^{\phi}_t f(x) = \int_{[0,\infty)} \widehat P_s f(x) \,\mathbb{P}(S_t \in ds), \end{gather*} $$
$$ \begin{gather*} P^{\phi}_t f(x) = \int_{[0,\infty)} P_s f(x) \,\mathbb{P}(S_t \in ds), \quad \widehat P^{\phi}_t f(x) = \int_{[0,\infty)} \widehat P_s f(x) \,\mathbb{P}(S_t \in ds), \end{gather*} $$
for
![]() $f \in L^2(M,\mu )$
or
$f \in L^2(M,\mu )$
or
![]() $f \in L^{\infty }(M,\mu )$
. It is obvious that these formulas define contractions on
$f \in L^{\infty }(M,\mu )$
. It is obvious that these formulas define contractions on
![]() $f \in L^2(M,\mu )$
, and the weak duality relation described in Section 7.1 holds. Moreover, these semigroups inherit the Feller property, the strong Feller property (provided that
$f \in L^2(M,\mu )$
, and the weak duality relation described in Section 7.1 holds. Moreover, these semigroups inherit the Feller property, the strong Feller property (provided that
![]() $S_t$
is not a compound Poisson subordinator), and the positivity improving property from the semigroups
$S_t$
is not a compound Poisson subordinator), and the positivity improving property from the semigroups
![]() $\{P_t: t \geqslant 0\}$
and
$\{P_t: t \geqslant 0\}$
and
![]() $\{\widehat P_t: t \geqslant 0\}$
. The only regularity property that requires an additional assumption is ultracontractivity: Suppose that
$\{\widehat P_t: t \geqslant 0\}$
. The only regularity property that requires an additional assumption is ultracontractivity: Suppose that
![]() $P_t, \widehat P_t$
are bounded operators from
$P_t, \widehat P_t$
are bounded operators from
![]() $L^2(M,\mu )$
to
$L^2(M,\mu )$
to
![]() $L^{\infty }(M,\mu )$
for every
$L^{\infty }(M,\mu )$
for every
![]() $t>0$
. By Remark 2.1, this is equivalent to the boundedness from
$t>0$
. By Remark 2.1, this is equivalent to the boundedness from
![]() $L^1(M,\mu )$
to
$L^1(M,\mu )$
to
![]() $L^{\infty }(M,\mu )$
, for any
$L^{\infty }(M,\mu )$
, for any
![]() $t>0$
. Therefore, ultracontractivity of the subordinate semigroup and its dual is ensured by the assumption that
$t>0$
. Therefore, ultracontractivity of the subordinate semigroup and its dual is ensured by the assumption that
 $$ \begin{gather*} \left\|P^{\phi}_t\right\|_{1,\infty} \leqslant \int_{[0,\infty)} \left\|P_s\right\|_{1,\infty} \mathbb{P}(S_t \in ds) < \infty, \quad t>0. \end{gather*} $$
$$ \begin{gather*} \left\|P^{\phi}_t\right\|_{1,\infty} \leqslant \int_{[0,\infty)} \left\|P_s\right\|_{1,\infty} \mathbb{P}(S_t \in ds) < \infty, \quad t>0. \end{gather*} $$
7.2. Progressive uniform exponential quasi-ergodicity for the harmonic oscillator
Let
![]() $H= -\Delta +|x|^2$
be the Schrödinger operator acting in
$H= -\Delta +|x|^2$
be the Schrödinger operator acting in
![]() $L^2(\mathbb {R}^d,dx)$
, and denote by
$L^2(\mathbb {R}^d,dx)$
, and denote by
![]() $U_t = e^{-tH}$
,
$U_t = e^{-tH}$
,
![]() $t \geqslant 0$
, the operators of the corresponding Schrödinger semigroup. It is well known that, for every
$t \geqslant 0$
, the operators of the corresponding Schrödinger semigroup. It is well known that, for every
![]() $t>0$
,
$t>0$
,
![]() $U_t$
is a compact, self-adjoint and positivity-improving integral operator with the kernel
$U_t$
is a compact, self-adjoint and positivity-improving integral operator with the kernel
 $$ \begin{align} u_t(x,y) = (2 \pi \sinh(2t))^{-d/2} \exp\left(-\frac{1}{4}\left(\tanh(t)|x+y|^2+ \coth(t)|x-y|^2\right)\right) \end{align} $$
$$ \begin{align} u_t(x,y) = (2 \pi \sinh(2t))^{-d/2} \exp\left(-\frac{1}{4}\left(\tanh(t)|x+y|^2+ \coth(t)|x-y|^2\right)\right) \end{align} $$
(see, for example, [Reference Stempak and Torrea60, (1.4)]. In particular, the assumptions ( A0)–( A3) are satisfied. The ground state eigenfunction and eigenvalue are given by
and (see [Reference Stempak and Torrea60, Proposition 3.3]Footnote 3)

It is easy to check that the semigroup
![]() $\left \{U_t: t \geqslant 0 \right \}$
is not aGSD; cf. [Reference Kaleta, Kwaśnicki and Lőrinczi24, Example 4.4]; in particular, using Corollary 4.4, it is not uniformly quasi-ergodic (see also the discussion in [Reference Knobloch and Partzsch31, Section 4.3]). We will show that our present results can be directly used to describe the true quasi-ergodic properties of this semigroup.
$\left \{U_t: t \geqslant 0 \right \}$
is not aGSD; cf. [Reference Kaleta, Kwaśnicki and Lőrinczi24, Example 4.4]; in particular, using Corollary 4.4, it is not uniformly quasi-ergodic (see also the discussion in [Reference Knobloch and Partzsch31, Section 4.3]). We will show that our present results can be directly used to describe the true quasi-ergodic properties of this semigroup.
First of all, observe that (7.12) shows that the heat content ![]() is finite for every
is finite for every
![]() $t>0$
, so that our results from Section 3 apply. In particular, Theorem 3.4 ensures that the semigroup
$t>0$
, so that our results from Section 3 apply. In particular, Theorem 3.4 ensures that the semigroup
![]() $\left \{U_t: t \geqslant 0 \right \}$
is exponentially quasi-ergodic for every finite initial distribution, and the limiting measure
$\left \{U_t: t \geqslant 0 \right \}$
is exponentially quasi-ergodic for every finite initial distribution, and the limiting measure
 $$ \begin{gather*} m(dx) = \frac{\phi_0(x)}{\left\|\phi_0\right\|_1}\, dx = \frac{1}{(2\pi)^{d/2}} e^{-\frac{|x|^2}{2}}\, dx \end{gather*} $$
$$ \begin{gather*} m(dx) = \frac{\phi_0(x)}{\left\|\phi_0\right\|_1}\, dx = \frac{1}{(2\pi)^{d/2}} e^{-\frac{|x|^2}{2}}\, dx \end{gather*} $$
is the only quasi-stationary measure of
![]() $\left \{U_t: t \geqslant 0 \right \}$
. By Corollary 3.5, we also get a pointwise version with explicit space-rate
$\left \{U_t: t \geqslant 0 \right \}$
. By Corollary 3.5, we also get a pointwise version with explicit space-rate

which is uniform on compact sets.
We will show that the quasi-ergodicity is progressively uniform. Observe that the semigroup
![]() $\big \{U_t:t \geqslant 0\big \}$
is pGSD; cf. Definition 4.2.b).
$\big \{U_t:t \geqslant 0\big \}$
is pGSD; cf. Definition 4.2.b).
Proposition 7.3. Let
![]() $x \in \mathbb {R}^d$
,
$x \in \mathbb {R}^d$
,
![]() $t>0$
and
$t>0$
and
![]() $C>0$
. Then
$C>0$
. Then

In particular, if
![]() $C < (2\sqrt {\pi })^{d/2}$
, the right-hand side is void for large t, and if
$C < (2\sqrt {\pi })^{d/2}$
, the right-hand side is void for large t, and if
![]() $C = (2\sqrt {\pi })^{d/2}$
, then the inequality on the right-hand side defines a bounded set of x for large t’s.
$C = (2\sqrt {\pi })^{d/2}$
, then the inequality on the right-hand side defines a bounded set of x for large t’s.
Proof. Because of (7.11) and (7.12), the inequality on the left-hand side reads
 $$ \begin{gather*} \exp\left[{|x|^2 \left(\frac{e^{-2t}}{e^{2t}+e^{-2t}}\right)}\right] \leqslant C \pi^{-\frac{d}{4}} \left(\frac{e^{2t}+e^{-2t}}{2}\right)^{\frac{d}{2}} e^{-dt} = C (2 \sqrt{\pi})^{-\frac{d}{2}} (1+e^{-4t})^{\frac{d}{2}}, \end{gather*} $$
$$ \begin{gather*} \exp\left[{|x|^2 \left(\frac{e^{-2t}}{e^{2t}+e^{-2t}}\right)}\right] \leqslant C \pi^{-\frac{d}{4}} \left(\frac{e^{2t}+e^{-2t}}{2}\right)^{\frac{d}{2}} e^{-dt} = C (2 \sqrt{\pi})^{-\frac{d}{2}} (1+e^{-4t})^{\frac{d}{2}}, \end{gather*} $$
which can be equivalently rewritten as
 $$ \begin{align*} |x|^2 \leqslant \big(1+e^{4t}\big) \left(\log C - \frac{d}{2}\log (2\sqrt{\pi}) + \frac{d}{2} \log (1+e^{-4t})\right).\\[-42pt] \end{align*} $$
$$ \begin{align*} |x|^2 \leqslant \big(1+e^{4t}\big) \left(\log C - \frac{d}{2}\log (2\sqrt{\pi}) + \frac{d}{2} \log (1+e^{-4t})\right).\\[-42pt] \end{align*} $$
Assume now that
![]() $C> (2\sqrt {\pi })^{d/2}$
and write
$C> (2\sqrt {\pi })^{d/2}$
and write
 $$ \begin{gather*} \rho(t):= K e^{2t} \sqrt{\left(1+e^{-4t}\right)\left(1 + \frac{d}{2K^2} \log (1+e^{-4t})\right)}, \quad t \geqslant 1, \end{gather*} $$
$$ \begin{gather*} \rho(t):= K e^{2t} \sqrt{\left(1+e^{-4t}\right)\left(1 + \frac{d}{2K^2} \log (1+e^{-4t})\right)}, \quad t \geqslant 1, \end{gather*} $$
where
![]() $K = \sqrt {\log \big (C/(2\sqrt {\pi })^{d/2}\big )}$
. Clearly, we have
$K = \sqrt {\log \big (C/(2\sqrt {\pi })^{d/2}\big )}$
. Clearly, we have
![]() $\rho (t) = K e^{2t} (1+o(1))$
, as
$\rho (t) = K e^{2t} (1+o(1))$
, as
![]() $t \to \infty $
. It follows from Proposition 7.3 that the semigroup
$t \to \infty $
. It follows from Proposition 7.3 that the semigroup
![]() $\left \{U_t: t \geqslant 0 \right \}$
is pGSD with the exhausting family
$\left \{U_t: t \geqslant 0 \right \}$
is pGSD with the exhausting family
![]() $\left \{K_t: t \geqslant 1\right \}$
where
$\left \{K_t: t \geqslant 1\right \}$
where
![]() $K_t = \overline {B}_{\rho (t)}(0)$
; that is,
$K_t = \overline {B}_{\rho (t)}(0)$
; that is,
Therefore, we can apply Theorem 5.2 to show that the progressive exponential uniform quasi-ergodicity holds on any space
![]() $L^p$
; it is easily seen from (7.12) that the assumption (
A4) holds for every
$L^p$
; it is easily seen from (7.12) that the assumption (
A4) holds for every
![]() $t_0>0$
. More precisely, for every
$t_0>0$
. More precisely, for every
![]() $a \in (0,1)$
and
$a \in (0,1)$
and
![]() $p \in [1,\infty ]$
, there are constants
$p \in [1,\infty ]$
, there are constants
![]() $C_1, C_2>0$
such that
$C_1, C_2>0$
such that

for sufficiently large
![]() $t>1$
.
$t>1$
.
It is interesting to note that one can use (7.10) and (7.12) to verify the following: for a family of measures
![]() $\big \{\sigma _t\big \}_{t \geqslant 1}$
given by
$\big \{\sigma _t\big \}_{t \geqslant 1}$
given by
![]() $\sigma _t = \delta _{x_t}$
with
$\sigma _t = \delta _{x_t}$
with
![]() $x_t = (e^{2t}x_0)/2$
where
$x_t = (e^{2t}x_0)/2$
where
![]() $x_0 \in \mathbb {R}^d$
is fixed and for
$x_0 \in \mathbb {R}^d$
is fixed and for ![]() where K is a Borel set of finite Lebesgue measure, we have
where K is a Borel set of finite Lebesgue measure, we have

This was first noticed in [Reference Knobloch and Partzsch31, p. 135] for
![]() $d=1$
; the aim was to show that the quasi-ergodicity property for the harmonic oscillator is not uniform in
$d=1$
; the aim was to show that the quasi-ergodicity property for the harmonic oscillator is not uniform in
![]() $\mathbb {R}$
(note that the authors of that paper work with a Schrödinger operator with rescaled kinetic term; that is,
$\mathbb {R}$
(note that the authors of that paper work with a Schrödinger operator with rescaled kinetic term; that is,
![]() ${H f = (1/2) f" + |x|^2 f}$
).
${H f = (1/2) f" + |x|^2 f}$
).
We can now see more. Indeed, (7.15) shows that the convergence in (7.14) cannot be uniform in the sets
![]() $K_t$
that come from the pGSD property (7.13) – one can choose
$K_t$
that come from the pGSD property (7.13) – one can choose
![]() $x_0$
is such a way that
$x_0$
is such a way that
![]() $x_t \in K_t$
for sufficiently large t. This means that Theorem 5.2 is optimal in the sense that, in general, the pGSD property with the exhausting family
$x_t \in K_t$
for sufficiently large t. This means that Theorem 5.2 is optimal in the sense that, in general, the pGSD property with the exhausting family
![]() $\left \{K_{t} : t \geqslant t_0\right \}$
implies the progressive exponential quasi-ergodicity with
$\left \{K_{t} : t \geqslant t_0\right \}$
implies the progressive exponential quasi-ergodicity with
![]() $\left \{K_{at} : t \geqslant t_0/\theta \right \}$
only for
$\left \{K_{at} : t \geqslant t_0/\theta \right \}$
only for
![]() $a < 1$
; cf. Remark 5.3.
$a < 1$
; cf. Remark 5.3.
7.3. Semigroups of non-local Schrödinger operators in the DJP setting
One of the main motivations for this paper was to describe the quasi-ergodic properties of the Schrödinger semigroups studied in a recent paper [Reference Kaleta and Schilling26]. These are evolution semigroups that belong to non-local Schrödinger operators of the form
![]() $H=-L+V$
, where L is the generator of a symmetric Lévy process
$H=-L+V$
, where L is the generator of a symmetric Lévy process
![]() $\{X_t: t \geqslant 0\}$
(so-called Lévy operator) with the direct jump property (DJP in short) in
$\{X_t: t \geqslant 0\}$
(so-called Lévy operator) with the direct jump property (DJP in short) in
![]() $\mathbb {R}^d$
,
$\mathbb {R}^d$
,
![]() $d \geqslant 1$
, and V is a sufficiently regular confining potential. Working in that generality, we identified in [Reference Kaleta and Schilling26] a new regularity property of compact semigroups in
$d \geqslant 1$
, and V is a sufficiently regular confining potential. Working in that generality, we identified in [Reference Kaleta and Schilling26] a new regularity property of compact semigroups in
![]() $L^2$
, that we called progressive intrinsic ultracontractivity (pIUC in short). It means that the regularity of the semigroup improves as
$L^2$
, that we called progressive intrinsic ultracontractivity (pIUC in short). It means that the regularity of the semigroup improves as
![]() $t \to \infty $
. We now want to understand what is the impact of pIUC on the quasi-ergodic properties of the semigroup.
$t \to \infty $
. We now want to understand what is the impact of pIUC on the quasi-ergodic properties of the semigroup.
The class of processes that we consider in this section consists of symmetric (self-dual) and strong Feller Lévy processes (cf. Section 7.1.1, also for notation). In addition, we have to impose some extra regularity conditions on the density
![]() $p_t(x)$
and the Lévy measure
$p_t(x)$
and the Lévy measure
![]() $\nu $
(Assumptions (A1)–(A2) in [Reference Kaleta and Schilling26]; we do not give details here). The key property is the following: we assume that the Lévy measure
$\nu $
(Assumptions (A1)–(A2) in [Reference Kaleta and Schilling26]; we do not give details here). The key property is the following: we assume that the Lévy measure
![]() $\nu (dx)$
has a density
$\nu (dx)$
has a density
![]() $\nu (x) \, dx$
and that there exists a decreasing ‘profile’ function
$\nu (x) \, dx$
and that there exists a decreasing ‘profile’ function
![]() $f:(0,\infty ) \to (0,\infty )$
such that
$f:(0,\infty ) \to (0,\infty )$
such that
![]() $\nu (x) \asymp f(|x|)$
,
$\nu (x) \asymp f(|x|)$
,
![]() $x \neq 0$
, and
$x \neq 0$
, and
for a constant
![]() $c>0$
, where
$c>0$
, where
![]() $f_1:= f \wedge 1$
. This condition has a very suggestive probabilistic interpretation, and therefore, it is called the direct jump property (DJP). Note that this class contains many examples of jump Lévy processes and the corresponding Lévy operators which play an important role in various applications. For example, it includes the
$f_1:= f \wedge 1$
. This condition has a very suggestive probabilistic interpretation, and therefore, it is called the direct jump property (DJP). Note that this class contains many examples of jump Lévy processes and the corresponding Lévy operators which play an important role in various applications. For example, it includes the
-
• fractional Laplace operator
 $L=-(-\Delta )^{\alpha /2}$
,
$L=-(-\Delta )^{\alpha /2}$
,
 $\alpha \in (0,2)$
(being the generator of the isotropic
$\alpha \in (0,2)$
(being the generator of the isotropic
 $\alpha $
-stable process); here,
$\alpha $
-stable process); here,
 $\nu (x) = c_{d,\alpha } |x|^{-d-\alpha }$
;
$\nu (x) = c_{d,\alpha } |x|^{-d-\alpha }$
; -
• relativistic operator
 $L=-(-\Delta +m^{2/\alpha })^{\alpha /2}+m$
,
$L=-(-\Delta +m^{2/\alpha })^{\alpha /2}+m$
,
 $\alpha \in (0,2)$
,
$\alpha \in (0,2)$
,
 $m>0$
(being the generator of the isotropic relativistic
$m>0$
(being the generator of the isotropic relativistic
 $\alpha $
-stable process); here,
$\alpha $
-stable process); here,
 ${\nu (x) \asymp e^{-m^{1/\alpha }|x|} (1 \wedge |x|)^{-\frac {d+\alpha -1}{2}} |x|^{-\frac {d+\alpha +1}{2}}}$
.
${\nu (x) \asymp e^{-m^{1/\alpha }|x|} (1 \wedge |x|)^{-\frac {d+\alpha -1}{2}} |x|^{-\frac {d+\alpha +1}{2}}}$
.
We assume that
![]() $V \in L^{\infty }_{\mathrm {loc}}(\mathbb {R}^d,dx)$
is a confining potential (i.e.,
$V \in L^{\infty }_{\mathrm {loc}}(\mathbb {R}^d,dx)$
is a confining potential (i.e.,
![]() $V(x) \to \infty $
as
$V(x) \to \infty $
as
![]() $|x| \to \infty $
) such that there is a an increasing profile
$|x| \to \infty $
) such that there is a an increasing profile
![]() $g:[0,\infty ) \to (0,\infty )$
, growing at infinity not faster than an exponential function, and there are constants
$g:[0,\infty ) \to (0,\infty )$
, growing at infinity not faster than an exponential function, and there are constants
![]() $c_1, c_2 \geqslant 1$
such that
$c_1, c_2 \geqslant 1$
such that
![]() $c_1^{-1} g(|x|) \leqslant V(x) \leqslant c_1 g(|x|)$
, for all
$c_1^{-1} g(|x|) \leqslant V(x) \leqslant c_1 g(|x|)$
, for all
![]() $|x| \geqslant c_2$
; see the detailed statement in [Reference Kaleta and Schilling26, Assumption (A3)].
$|x| \geqslant c_2$
; see the detailed statement in [Reference Kaleta and Schilling26, Assumption (A3)].
The Schrödinger operator
![]() $H=-L+V$
is well defined, bounded below and self-adjoint in
$H=-L+V$
is well defined, bounded below and self-adjoint in
![]() $L^2(\mathbb {R}^d,dx)$
. We denote by
$L^2(\mathbb {R}^d,dx)$
. We denote by
![]() $U_t = e^{-tH}$
,
$U_t = e^{-tH}$
,
![]() $t \geqslant 0$
, the operators of the corresponding evolution semigroup. They are known to have the following probabilistic Feynman–Kac representation:
$t \geqslant 0$
, the operators of the corresponding evolution semigroup. They are known to have the following probabilistic Feynman–Kac representation:
The operators
![]() $U_t$
are self-adjoint, and by [Reference Kaleta and Schilling26, Lemma 2.3] (or Lemma 7.1) and Lemma 7.2.a), all regularity assumptions (
A0)–(
A3) are satisfied and (
A4) follows from the proof of Lemma 7.2.a). Our standard reference for self-adjoint Schrödinger operators and the Feynman–Kac semigroups is the monograph [Reference Demuth and van Casteren17].
$U_t$
are self-adjoint, and by [Reference Kaleta and Schilling26, Lemma 2.3] (or Lemma 7.1) and Lemma 7.2.a), all regularity assumptions (
A0)–(
A3) are satisfied and (
A4) follows from the proof of Lemma 7.2.a). Our standard reference for self-adjoint Schrödinger operators and the Feynman–Kac semigroups is the monograph [Reference Demuth and van Casteren17].
We will now show how our present results apply to these semigroups. The discussion will be divided into three parts.
(1) Heat content and exponential quasi-ergodicity. First of all, due to Lemma 7.2.b), we know that
 $$ \begin{align} \liminf_{|x| \to \infty} \frac{V(x)}{\log|x|}>0 \qquad \Longleftrightarrow \qquad \exists \, t_1>0 \::\: Z(t_1)< \infty, \end{align} $$
$$ \begin{align} \liminf_{|x| \to \infty} \frac{V(x)}{\log|x|}>0 \qquad \Longleftrightarrow \qquad \exists \, t_1>0 \::\: Z(t_1)< \infty, \end{align} $$
and our results in Section 3 apply. More precisely, by Theorem 3.4, the semigroup
![]() $\left \{U_t: t \geqslant 0 \right \}$
is exponentially quasi-ergodic for every finite initial distribution, and the limiting measure
$\left \{U_t: t \geqslant 0 \right \}$
is exponentially quasi-ergodic for every finite initial distribution, and the limiting measure
 $$ \begin{gather*} m(dx) = \frac{\phi_0(x)}{\left\|\phi_0\right\|_1}\, dx, \end{gather*} $$
$$ \begin{gather*} m(dx) = \frac{\phi_0(x)}{\left\|\phi_0\right\|_1}\, dx, \end{gather*} $$
where
![]() $\phi _0(x)$
is the ground state of the operator H, is the only quasi-stationary measure of
$\phi _0(x)$
is the ground state of the operator H, is the only quasi-stationary measure of
![]() $\left \{U_t: t \geqslant 0 \right \}$
. Furthermore, in Corollary 3.5, we obtain a pointwise version with the space-rate
$\left \{U_t: t \geqslant 0 \right \}$
. Furthermore, in Corollary 3.5, we obtain a pointwise version with the space-rate ![]() which is uniform on compact sets. By [Reference Kaleta and Lőrinczi25, Corollary 2.2], there is a constant
which is uniform on compact sets. By [Reference Kaleta and Lőrinczi25, Corollary 2.2], there is a constant
![]() $c_3>0$
such that
$c_3>0$
such that
 $$ \begin{gather*} \phi_0(x) \geqslant c_6 \left(1 \wedge \frac{\nu(x)}{V(x)}\right), \quad x \in \mathbb{R}^d \end{gather*} $$
$$ \begin{gather*} \phi_0(x) \geqslant c_6 \left(1 \wedge \frac{\nu(x)}{V(x)}\right), \quad x \in \mathbb{R}^d \end{gather*} $$
(this remains true for potentials without radial profiles). However, we always have
which leads to the following explicit estimate of the rate

The function on the right-hand side tends to infinity as
![]() $|x| \to \infty $
, but it is bounded on compact sets. Better estimates for
$|x| \to \infty $
, but it is bounded on compact sets. Better estimates for ![]() can be found in [Reference Kaleta and Schilling26, Theorem 4.8]. Observe that the sufficient condition in (7.18) does not depend on
can be found in [Reference Kaleta and Schilling26, Theorem 4.8]. Observe that the sufficient condition in (7.18) does not depend on
![]() $\nu $
.
$\nu $
.
(2) aGSD regime and uniform exponential quasi-ergodicity. By [Reference Kaleta and Lőrinczi25, Theorem 2.6],

Recall that the property on the right-hand side is called aGSD; see Definition 4.2.a). If we are in the aGSD regime – that is, if the growth of the potential is sufficiently large with respect to
![]() $|\log \nu (x)|$
– then the exponential quasi-ergodicity in Corollary 3.5 discussed above becomes uniform on the full space
$|\log \nu (x)|$
– then the exponential quasi-ergodicity in Corollary 3.5 discussed above becomes uniform on the full space
![]() $\mathbb {R}^d$
. This is exactly what we saw in Corollary 4.4.a). The same conclusion follows from [Reference Knobloch and Partzsch31, Theorem 1, Corollary 2]. However, now we get much more. Combining Corollary 4.4 and (7.20), we get that the uniform quasi-ergodicity of the semigroup
$\mathbb {R}^d$
. This is exactly what we saw in Corollary 4.4.a). The same conclusion follows from [Reference Knobloch and Partzsch31, Theorem 1, Corollary 2]. However, now we get much more. Combining Corollary 4.4 and (7.20), we get that the uniform quasi-ergodicity of the semigroup
![]() $\left \{U_t: t \geqslant 0 \right \}$
is equivalent to the condition
$\left \{U_t: t \geqslant 0 \right \}$
is equivalent to the condition
 $$ \begin{gather*} \liminf_{|x| \to \infty} \frac{V(x)}{|\log\nu(x)|}>0. \end{gather*} $$
$$ \begin{gather*} \liminf_{|x| \to \infty} \frac{V(x)}{|\log\nu(x)|}>0. \end{gather*} $$
If
![]() $\nu (x)$
has polynomial decay at infinity (as is, for example, the case for the fractional Laplacian), then
$\nu (x)$
has polynomial decay at infinity (as is, for example, the case for the fractional Laplacian), then
![]() $|\log \nu (x)| \asymp \log |x|$
, for
$|\log \nu (x)| \asymp \log |x|$
, for
![]() $|x|$
large enough, and the properties in (7.18) and (7.20) coincide. However, if
$|x|$
large enough, and the properties in (7.18) and (7.20) coincide. However, if
![]() $\nu $
decays at infinity faster than any polynomial, then (7.20) is more restrictive than (7.18). For example, if
$\nu $
decays at infinity faster than any polynomial, then (7.20) is more restrictive than (7.18). For example, if
![]() $\nu (x)$
is exponential at infinity (e.g., for relativistic operators), then
$\nu (x)$
is exponential at infinity (e.g., for relativistic operators), then
![]() $|\log \nu (x)| \asymp |x|$
, for large
$|\log \nu (x)| \asymp |x|$
, for large
![]() $|x|$
.
$|x|$
.
(3) pGSD and progressive uniform quasi-ergodicity. Finally, we characterize the quasi-ergodic behavior of the Schrödinger semigroups
![]() $\left \{U_t: t \geqslant 0 \right \}$
with confining potentials as above which do not satisfy (7.20), no matter how slow the potential may grow at infinity; this brings us out of the aGSD regime. Note that this problem was completely open. Since we want to be here as sharp as possible, we have to monitor precisely the threshold between the aGSD and the non-aGSD regime. For this reason, we follow [Reference Kaleta and Schilling26, Assumption (A4)] and impose an additional technical condition on the profile g of the potential V. More precisely, we require that g depends on the profile f of the Lévy density
$\left \{U_t: t \geqslant 0 \right \}$
with confining potentials as above which do not satisfy (7.20), no matter how slow the potential may grow at infinity; this brings us out of the aGSD regime. Note that this problem was completely open. Since we want to be here as sharp as possible, we have to monitor precisely the threshold between the aGSD and the non-aGSD regime. For this reason, we follow [Reference Kaleta and Schilling26, Assumption (A4)] and impose an additional technical condition on the profile g of the potential V. More precisely, we require that g depends on the profile f of the Lévy density
![]() $\nu $
in a sufficiently regular way: we consider
$\nu $
in a sufficiently regular way: we consider
![]() $R_0>0$
such that
$R_0>0$
such that
![]() $f(R_0)<1$
and assume that
$f(R_0)<1$
and assume that
![]() $g(r) = h(|\log f(r)|)$
,
$g(r) = h(|\log f(r)|)$
,
![]() $r \geqslant R_0$
, for an increasing function
$r \geqslant R_0$
, for an increasing function
![]() $h:[|\log f(R_0)|,\infty ) \to (0,\infty )$
such that
$h:[|\log f(R_0)|,\infty ) \to (0,\infty )$
such that
![]() $h(s)/s$
is monotone. Under this assumption, the class of Schrödinger semigroups
$h(s)/s$
is monotone. Under this assumption, the class of Schrödinger semigroups
![]() $\left \{U_t: t \geqslant 0 \right \}$
with Lévy densities
$\left \{U_t: t \geqslant 0 \right \}$
with Lévy densities
![]() $\nu $
and potentials V is divided into two classes:
$\nu $
and potentials V is divided into two classes:
-
a) (aGSD regime):
 $\liminf _{|x| \to \infty } \frac {V(x)}{|\log \nu (x)|}>0$
, i.e. (7.20) holds;
$\liminf _{|x| \to \infty } \frac {V(x)}{|\log \nu (x)|}>0$
, i.e. (7.20) holds; -
b) (non-aGSD regime):
 $\lim _{|x| \to \infty } \frac {V(x)}{|\log \nu (x)|} =0$
;
$\lim _{|x| \to \infty } \frac {V(x)}{|\log \nu (x)|} =0$
;
cf. [Reference Kaleta and Schilling26, Remark 5.1]. We already know from Part (2) that in the aGSD regime, the Schrödinger semigroup is uniformly exponentially quasi-ergodic, and, in fact, we have the equivalence of these two properties.
The rest of this section will be devoted to the analysis of the quasi-ergodic behavior in the non-aGSD regime. Of course, if (7.18) holds, then we know from Part (1) above that we have the exponential quasi-ergodicity with semi-explicit rate, which is uniform on compact sets. With [Reference Kaleta and Schilling26, Corollary 5.6 b)], we can now give even better estimates for the rate (7.19)

for some
![]() $c_4, c_5>0$
. Our theorems from Section 5 now yield much stronger results. In the paper [Reference Kaleta and Schilling26], we identify a new large-time regularity property of compact semigroups, which we call progressive intrinsic ultracontractivity (pIUC). This property holds for semigroups considered here. In [Reference Kaleta and Schilling26, Corollary 5.6 b)], we show that pIUC implies the following two-sided sharp estimates: there exist
$c_4, c_5>0$
. Our theorems from Section 5 now yield much stronger results. In the paper [Reference Kaleta and Schilling26], we identify a new large-time regularity property of compact semigroups, which we call progressive intrinsic ultracontractivity (pIUC). This property holds for semigroups considered here. In [Reference Kaleta and Schilling26, Corollary 5.6 b)], we show that pIUC implies the following two-sided sharp estimates: there exist
![]() $\theta \in (0,1)$
,
$\theta \in (0,1)$
,
![]() $t_2>0$
and an increasing function
$t_2>0$
and an increasing function
![]() $\rho : [t_2, \infty ) \to (0,\infty )$
, with
$\rho : [t_2, \infty ) \to (0,\infty )$
, with
![]() $\lim _{t \to \infty } \rho (t) = \infty $
, such that
$\lim _{t \to \infty } \rho (t) = \infty $
, such that

(note that the comparison constants are uniform in x and t!). The function
![]() $\rho $
is the right-continuous generalized inverse function of
$\rho $
is the right-continuous generalized inverse function of
![]() $r \mapsto |\log f(r)|/g(r)$
; see [Reference Kaleta and Schilling26, Lemma 5.2]. Note that (7.21) is the progressive ground state domination (pGSD) property; cf. Definition 4.2.b).
$r \mapsto |\log f(r)|/g(r)$
; see [Reference Kaleta and Schilling26, Lemma 5.2]. Note that (7.21) is the progressive ground state domination (pGSD) property; cf. Definition 4.2.b).
Therefore, we see that
![]() $\left \{U_t: t \geqslant 0 \right \}$
is pGSD with the exhausting family
$\left \{U_t: t \geqslant 0 \right \}$
is pGSD with the exhausting family
![]() $\left \{K_t: t \geqslant t_2/\theta \right \}$
where
$\left \{K_t: t \geqslant t_2/\theta \right \}$
where
![]() $K_t = \overline {B}_{\rho (\theta t)}(0)$
, and we can apply Theorem 5.2 to show that the progressive uniform quasi-ergodicity on any space
$K_t = \overline {B}_{\rho (\theta t)}(0)$
, and we can apply Theorem 5.2 to show that the progressive uniform quasi-ergodicity on any space
![]() $L^p$
holds. We obtain that there exist
$L^p$
holds. We obtain that there exist
![]() $\gamma , t_0>0$
such that for every
$\gamma , t_0>0$
such that for every
![]() $a, b \in (0,1)$
such that
$a, b \in (0,1)$
such that
![]() $a+2b=1$
and
$a+2b=1$
and
![]() $p \in [1,\infty ]$
, there is a constant
$p \in [1,\infty ]$
, there is a constant
![]() $c_6>0$
such that
$c_6>0$
such that

where
Because of Theorem 5.5, the measure m is the only quasi-stationary distribution of the Schrödinger semigroup
![]() $\left \{U_t: t \geqslant 0 \right \}$
– no matter how slowly V grows at infinity. We need to verify only the condition (5.5). To this end, we observe that by [Reference Kaleta and Schilling26, Corollary 5.6 b)], there are constants
$\left \{U_t: t \geqslant 0 \right \}$
– no matter how slowly V grows at infinity. We need to verify only the condition (5.5). To this end, we observe that by [Reference Kaleta and Schilling26, Corollary 5.6 b)], there are constants
![]() $c_7, c_8>0$
such that
$c_7, c_8>0$
such that
for sufficiently large values of t. Since
![]() $V(x) \to \infty $
as
$V(x) \to \infty $
as
![]() $|x| \to \infty $
and
$|x| \to \infty $
and
![]() $\rho (t) \to \infty $
as
$\rho (t) \to \infty $
as
![]() $t \to \infty $
, this implies (5.8), which is equivalent to (5.5).
$t \to \infty $
, this implies (5.8), which is equivalent to (5.5).
Example 7.4. Let us illustrate these results for two specific classes of Lévy measures and potentials. See Section 7.1.1 for the notation.
-
a) (polynomial Lévy densities; cf. [Reference Kaleta and Schilling26, Section 5.4, Example 5.7]): let
and let $$ \begin{gather*} \nu(x) \asymp |x|^{-d-\alpha} (e \vee |x|)^{-\delta}, \quad \alpha \in (0,2), \ \delta \geqslant 0, \end{gather*} $$
$$ \begin{gather*} \nu(x) \asymp |x|^{-d-\alpha} (e \vee |x|)^{-\delta}, \quad \alpha \in (0,2), \ \delta \geqslant 0, \end{gather*} $$
 $V(x) = (1 \vee \log |x|)^{\beta }$
,
$V(x) = (1 \vee \log |x|)^{\beta }$
,
 $\beta>0$
. Then we have the following:
$\beta>0$
. Then we have the following:
-
• if
 $\beta \geqslant 1$
, then the corresponding Schrödinger semigroup is in the aGSD regime and exponential uniform quasi-ergodicity holds; see Part (2) above;
$\beta \geqslant 1$
, then the corresponding Schrödinger semigroup is in the aGSD regime and exponential uniform quasi-ergodicity holds; see Part (2) above; -
• if
 $\beta \in (0,1)$
, then the semigroup is in the non-aGSD regime; it is pGSD and progressive uniform quasi-ergodicity holds; see Part (3). We have (7.22)for large values of t, with different constants
$\beta \in (0,1)$
, then the semigroup is in the non-aGSD regime; it is pGSD and progressive uniform quasi-ergodicity holds; see Part (3). We have (7.22)for large values of t, with different constants $$ \begin{align} \rho(t) = \exp\left(t^{1/(1-\beta)} \right) \quad \text{and} \quad \kappa_b(t) \asymp \exp\left(-c_9 \left(t \wedge t^{\frac{\beta}{1-\beta}}\right)\right), \end{align} $$
$$ \begin{align} \rho(t) = \exp\left(t^{1/(1-\beta)} \right) \quad \text{and} \quad \kappa_b(t) \asymp \exp\left(-c_9 \left(t \wedge t^{\frac{\beta}{1-\beta}}\right)\right), \end{align} $$
 $c_9$
in the lower and in the upper bound. The rate
$c_9$
in the lower and in the upper bound. The rate
 $\kappa _b(t)$
is exponential for
$\kappa _b(t)$
is exponential for
 $\beta \geqslant 1/2$
, and subexponential (stretched-exponential) for
$\beta \geqslant 1/2$
, and subexponential (stretched-exponential) for
 $\beta < 1/2$
.
$\beta < 1/2$
.
-
-
b) (exponential Lévy densities; cf. [Reference Kaleta and Schilling26, Section 5.5, Example 5.10]): let
and let $$ \begin{gather*} \nu(x) \asymp e^{-m|x|} (1 \wedge |x|)^{-d-\alpha} (1 \vee |x|)^{-\delta}, \quad m>0, \ \alpha \in (0,2), \ \delta > (d+1)/2, \end{gather*} $$
$$ \begin{gather*} \nu(x) \asymp e^{-m|x|} (1 \wedge |x|)^{-d-\alpha} (1 \vee |x|)^{-\delta}, \quad m>0, \ \alpha \in (0,2), \ \delta > (d+1)/2, \end{gather*} $$
 $V(x) = (1 \vee |x|)^{\beta }$
,
$V(x) = (1 \vee |x|)^{\beta }$
,
 $\beta>0$
. Then we have the following:
$\beta>0$
. Then we have the following:
-
• if
 $\beta \geqslant 1$
, then the corresponding Schrödinger semigroup is in the aGSD regime and exponential uniform quasi-ergodicity holds; see Part (2) above;
$\beta \geqslant 1$
, then the corresponding Schrödinger semigroup is in the aGSD regime and exponential uniform quasi-ergodicity holds; see Part (2) above; -
• if
 $\beta \in (0,1)$
, then the semigroup is in the non-aGSD regime; it is pGSD and progressive uniform quasi-ergodicity holds; see Part (3). We have for large values of t, but the rate
$\beta \in (0,1)$
, then the semigroup is in the non-aGSD regime; it is pGSD and progressive uniform quasi-ergodicity holds; see Part (3). We have for large values of t, but the rate $$ \begin{gather*} \rho(t) = t^{1/(1-\beta)} \end{gather*} $$
$$ \begin{gather*} \rho(t) = t^{1/(1-\beta)} \end{gather*} $$
 $\kappa _b(t)$
takes the same form as that in (7.22).
$\kappa _b(t)$
takes the same form as that in (7.22).
-
Theorem 4.6 also shows that any semigroup
![]() $\left \{U_t: t \geqslant 0 \right \}$
with finite heat content (for large times) is automatically pGSD; moreover, progressive uniform quasi-ergodicity holds with exponential time-rate. For polynomial Lévy densities, this result is not interesting as we already know that in this case, (7.18) is equivalent to (7.20). However, for faster decays, the assertions of the theorem are nontrivial. For instance, in the exponential case, one can check that Theorem 4.6 implies pGSD and progressive uniform quasi-ergodicity with the exhausting family
$\left \{U_t: t \geqslant 0 \right \}$
with finite heat content (for large times) is automatically pGSD; moreover, progressive uniform quasi-ergodicity holds with exponential time-rate. For polynomial Lévy densities, this result is not interesting as we already know that in this case, (7.18) is equivalent to (7.20). However, for faster decays, the assertions of the theorem are nontrivial. For instance, in the exponential case, one can check that Theorem 4.6 implies pGSD and progressive uniform quasi-ergodicity with the exhausting family
![]() $\left \{K_t: t \geqslant t_0 \right \}$
where
$\left \{K_t: t \geqslant t_0 \right \}$
where
![]() $K_t = \overline {B}_{c t}(0)$
, for a constant
$K_t = \overline {B}_{c t}(0)$
, for a constant
![]() $c>0$
.
$c>0$
.
Acknowledgements
K. Kaleta was supported by the Alexander von Humboldt Foundation (Germany) and by the National Science Centre (Poland) project OPUS-18 2019/35/B/ST1/02421. R.L. Schilling was supported through the DFG-NCN Beethoven Classic 3 project SCHI419/11-1 & NCN 2018/31/G/ST1/02252, the 6G-life project (BMBF programme ‘Souverän. Digital. Vernetzt.’ 16KISK001K) and the Dresden–Leipzig SCADS.AI centre. We are grateful for stimulating discussions with David Berger (Dresden), Krzysztof Bogdan (Wrocław), Tomasz Klimsiak (Toruń) and Paweł Sztonyk (Wrocław) on the topics of this paper. We would like to acknowledge the helpful comments of an anonymous referee.
Competing interest
The authors have no competing interests to declare that are relevant to the content of this article.


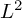
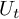
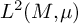
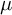
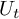
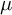
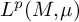
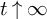
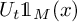 . We discuss several applications and illustrate our results with examples. This includes a complete description of quasi-ergodicity for a large class of semigroups corresponding to non-local Schrödinger operators with confining potentials.
. We discuss several applications and illustrate our results with examples. This includes a complete description of quasi-ergodicity for a large class of semigroups corresponding to non-local Schrödinger operators with confining potentials.














