No CrossRef data available.
Article contents
PROJECTIVELY FLAT FOLIATIONS
Part of:
Complex dynamical systems
Complex manifolds
Local differential geometry
Birational geometry
Published online by Cambridge University Press: 18 March 2025
Abstract
We describe the structure of regular codimension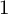 
$1$ foliations with numerically projectively flat tangent bundle on complex projective manifolds of dimension at least 
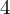$4$. Along the way, we prove that either the normal bundle of a regular codimension 
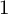$1$ foliation is pseudo-effective, or its conormal bundle is nef.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press
References
Aubin, T (1976) Équations du type Monge–Ampère sur les variétés kähleriennes compactes. C. R. Acad. Sci. Paris Sér. A-B 283 (3), Aiii, A119–A121.Google Scholar
Baum, PF and Bott, R (1970) On the zeros of meromorphic vector-fields. In Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham). New York: Springer, 29–47.CrossRefGoogle Scholar
Bauer, T, Campana, F, Eckl, T, Kebekus, S, Peternell, T, Rams, S, Szemberg, T and Wotzlaw, L (2002) A reduction map for nef line bundles. In Complex Geometry (Göttingen, 2000). Berlin: Springer, 27–36.CrossRefGoogle Scholar
Boucksom, S, Demailly, JP, Păun, M and Peternell, T (2013) The pseudo-effective cone of a compact Kähler manifold and varieties of negative Kodaira dimension. J. Algebraic Geom. 22 (2), 201–248.CrossRefGoogle Scholar
Beauville, A (1977) Variétés de Prym et jacobiennes intermédiaires. Ann. Sci. École Norm. Sup. (4) 10 (3), 309–391.CrossRefGoogle Scholar
Beauville, A (2000) Complex manifolds with split tangent bundle. In Complex Analysis and Algebraic Geometry. Berlin: de Gruyter, Berlin, 61–70.Google Scholar
Birkenhake, C and Lange, H (2004) Complex Abelian Varieties. 2nd augmented edn. Berlin: Springer, 2004.CrossRefGoogle Scholar
Bogomolov, F and McQuillan, M (2016) Rational curves on foliated varieties. In Foliation Theory in Algebraic Geometry, Simons Symp. Cham: Springer, 21–51.CrossRefGoogle Scholar
Barth, W, Peters, C and Van de Ven, A (1984) Compact Complex Surfaces, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 4. Berlin: Springer-Verlag. MR 749574CrossRefGoogle Scholar
Brunella, M (1997) Feuilletages holomorphes sur les surfaces complexes compactes. Ann. Sci. École Norm. Sup. (4)
30 (5), 569–594.CrossRefGoogle Scholar
Brunella, M (2004) Birational Geometry of Foliations, IMPA Mathematical Publications. Rio de Janeiro: Instituto de Matemática Pura e Aplicada (IMPA).Google Scholar
Catanese, F (2002) Deformation types of real and complex manifolds. In Contemporary Trends in Algebraic Geometry and Algebraic Topology (Tianjin, 2000), Nankai Tracts Math., vol. 5. River Edge, NJ: World Sci. Publ., 195–238.CrossRefGoogle Scholar
Campana, F, Claudon, B and Eyssidieux, P (2015) Représentations linéaires des groupes kählériens: factorisations et conjecture de Shafarevich linéaire. Compos. Math. 151 (2), 351–376.CrossRefGoogle Scholar
Campana, F, Koziarz, V and Păun, M (2012) Numerical character of the effectivity of adjoint line bundles. Ann. Inst. Fourier (Grenoble) 62 (1), 107–119.CrossRefGoogle Scholar
Claudon, B (2010) Invariance de la
$\varGamma$
-dimension pour certaines familles kählériennes de dimension 3. Math. Z. 266 (2), 265–284.CrossRefGoogle Scholar
$\varGamma$
-dimension pour certaines familles kählériennes de dimension 3. Math. Z. 266 (2), 265–284.CrossRefGoogle ScholarDruel, S and Lo Bianco, F (2022) Numerical characterization of some toric fiber bundles. Math. Z. 300 (4), 3357–3382.CrossRefGoogle Scholar
Debarre, O (1999) Tores et variétés abéliennes complexes, Cours Spécialisés [Specialized Courses], vol. 6. Paris: Société Mathématique de France; Les Ulis: EDP Sciences.Google Scholar
Debarre, O (2001) Higher-Dimensional Algebraic Geometry, Universitext. New York: Springer-Verlag.CrossRefGoogle Scholar
Druel, S and Guenancia, H (2018) A decomposition theorem for smoothable varieties with trivial canonical class. J. Éc. polytech. Math. 5, 117–147.CrossRefGoogle Scholar
Demailly, JP, Hacon, CD and Păun, M (2013) Extension theorems, non-vanishing and the existence of good minimal models. Acta Math. 210 (2), 203–259.CrossRefGoogle Scholar
Demailly, JP, Peternell, T and Schneider, M (1994) Compact complex manifolds with numerically effective tangent bundles. J. Algebraic Geom. 3 (2), 295–345.Google Scholar
Druel, S (2014) The Zariski–Lipman conjecture for log canonical spaces. Bull. Lond. Math. Soc. 46 (4), 827–835.CrossRefGoogle Scholar
Druel, S (2018) A decomposition theorem for singular spaces with trivial canonical class of dimension at most five. Invent. Math. 211 (1), 245–296.CrossRefGoogle Scholar
Druel, S (2021) Codimension 1 foliations with numerically trivial canonical class on singular spaces. Duke Math. J. 170 (1), 95–203.CrossRefGoogle Scholar
Druel, S (2024) Projectively flat log smooth pairs. Ann. Fac. Sci. Toulouse Math. Sér. 6, 33 (3), 611–645.CrossRefGoogle Scholar
Eisenbud, D (1995) Commutative Algebra. With a View toward Algebraic Geometry. Berlin: Springer-Verlag.Google Scholar
Figueredo, JP (2022) Codimension one regular foliations on rationally connected threefolds
. Bull. Braz. Math. Soc. (N.S.) 53 (4), 1131–1144.CrossRefGoogle Scholar
Greb, D, Kebekus, S, Kovács, Sándor J. and Peternell, T (2011) Differential forms on log canonical spaces. Publ. Math. Inst. Hautes Études Sci. (114), 87–169.CrossRefGoogle Scholar
Greb, D, Kebekus, S and Peternell, T (2016) Singular spaces with trivial canonical class. In Minimal Models and Extremal Rays (Kyoto, 2011), Adv. Stud. Pure Math., vol. 70. Tokyo: Math. Soc. Japan, 67–113.Google Scholar
Greb, D, Kebekus, S and Peternell, T (2021) Projectively flat klt varieties. J. Éc. polytech. Math. 8, 1005–1036.CrossRefGoogle Scholar
Gongyo, Y and Lehmann, B (2013) Reduction maps and minimal model theory. Compos. Math. 149 (2), 295–308.CrossRefGoogle Scholar
Griffiths, PA (1970) Periods of integrals on algebraic manifolds. III. Some global differential-geometric properties of the period mapping. Inst. Hautes Études Sci. Publ. Math. (38), 125–180.CrossRefGoogle Scholar
Grothendieck, A (1966) Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. III. Inst. Hautes Études Sci. Publ. Math. (28), 255.Google Scholar
Guenancia, H and Taji, B (2022) Orbifold stability and Miyaoka-Yau inequality for minimal pairs. Geom. Topol. 26 (4), 1435–1482.CrossRefGoogle Scholar
Hartshorne, R (1977) Algebraic Geometry, Graduate Texts in Mathematics, No. 52. New York: Springer-Verlag.CrossRefGoogle Scholar
Huybrechts, D and Lehn, M (1997)
The Geometry of Moduli Spaces of Sheaves, Aspects of Mathematics, E31. Braunschweig: Friedr. Vieweg & Sohn.CrossRefGoogle Scholar
Hacon, CD and McKernan, J (2007) On Shokurov’s rational connectedness conjecture. Duke Math. J. 138 (1), 119–136.CrossRefGoogle Scholar
Höring, A (2013) Manifolds with nef cotangent bundle. Asian J. Math. 17 (3), 561–568.CrossRefGoogle Scholar
Hu, Z (2016) Log canonical pairs over varieties with maximal Albanese dimension. Pure Appl. Math. Q. 12 (4), 543–571.CrossRefGoogle Scholar
Jouanolou, JP (1983) Théorèmes de Bertini et Applications, Progress in Mathematics, vol. 42. Boston: Birkhäuser Boston, Inc.
Google Scholar
Jahnke, P and Radloff, I (2013) Semistability of restricted tangent bundles and a question of I. Biswas. Internat. J. Math. 24 (1), 1250122, 15.CrossRefGoogle Scholar
Kawamata, Y (1985) Pluricanonical systems on minimal algebraic varieties. Invent. Math. 79 (3), 567–588.CrossRefGoogle Scholar
Kawamata, Y (1991) On the length of an extremal rational curve. Invent. Math. 105 (3), 609–611.CrossRefGoogle Scholar
Kollár, J and Mori, S (1998) Birational Geometry of Algebraic Varieties, Cambridge Tracts in Mathematics, vol. 134. Cambridge: Cambridge University Press. With the collaboration of C. H. Clemens and A. Corti, Translated from the 1998 Japanese original.CrossRefGoogle Scholar
Kawamata, Y, Matsuda, K and Matsuki, K (1987) Introduction to the minimal model problem. In Algebraic Geometry, Sendai, 1985, Adv. Stud. Pure Math., vol. 10. Amsterdam: North-Holland, Amsterdam, 283–360.CrossRefGoogle Scholar
Kobayashi, S (1987) Differential Geometry of Complex Vector Bundles, Publications of the Mathematical Society of Japan, vol. 15. Princeton, NJ: Princeton University Press. Kanô Memorial Lectures, 5.CrossRefGoogle Scholar
Kollár, J (1993) Shafarevich maps and plurigenera of algebraic varieties. Invent. Math. 113 (1), 177–215.CrossRefGoogle Scholar
Kollár, J (1996) Rational Curves on Algebraic Varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 32. Berlin: Springer-Verlag.CrossRefGoogle Scholar
Kebekus, S, Conde, LS and Toma, M (2007
) Rationally connected foliations after Bogomolov and McQuillan. J. Algebraic Geom. 16 (1), 65–81.CrossRefGoogle Scholar
Nakayama, N (1999) Compact Kähler manifolds whose universal covering spaces are biholomorphic to
${\mathbb{C}}^n$
. Preprint RIMS 12330.Google Scholar
${\mathbb{C}}^n$
. Preprint RIMS 12330.Google ScholarNakayama, N (2004) Zariski-Decomposition and Abundance, MSJ Memoirs, vol. 14. Tokyo: Mathematical Society of Japan.Google Scholar
Simpson, CT (1988) Constructing variations of Hodge structure using Yang–Mills theory and applications to uniformization. J. Amer. Math. Soc. 1 (4), 867–918.CrossRefGoogle Scholar
Simpson, CT (1992) Higgs bundles and local systems. Inst. Hautes Études Sci. Publ. Math. (75), 5–95.CrossRefGoogle Scholar
The Stacks Project Authors (2023) The Stacks Project. https://stacks.math.columbia.edu.Google Scholar
Touzet, F (2008) Feuilletages holomorphes de codimension un dont la classe canonique est triviale. Ann. Sci. Éc. Norm. Supér. (4) 41 (4), 655–668.Google Scholar
Touzet, F (2016) On the structure of codimension 1 foliations with pseudoeffective conormal bundle. In Foliation Theory in Algebraic Geometry, Simons Symp.: Cham Springer, 157–216.CrossRefGoogle Scholar
Ueno, K (1975) Classification Theory of Algebraic Varieties and Compact Complex Spaces, Lecture Notes in Mathematics, vol. 439. Berlin-New York: Springer-Verlag. Notes written in collaboration with P. Cherenack.CrossRefGoogle Scholar
Ueno, K (1978) On algebraic fibre spaces of abelian varieties. Math. Ann. 237 (1), 1–22.CrossRefGoogle Scholar
Viehweg, E and Zuo, K (2007) Arakelov inequalities and the uniformization of certain rigid Shimura varieties. J. Differential Geom. 77 (2), 291–352.CrossRefGoogle Scholar
Wang, HC (1954) Complex parallisable manifolds. Proc. Amer. Math. Soc. 5, 771–776.CrossRefGoogle Scholar
Wiśniewski, JA (1991) On contractions of extremal rays of Fano manifolds. J. Reine Angew. Math. 417, 141–157.Google Scholar
Yau, ST (1977) Calabi’s conjecture and some new results in algebraic geometry. Proc. Nat. Acad. Sci. U.S.A. 74 (5), 1798–1799.CrossRefGoogle ScholarPubMed