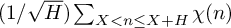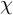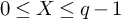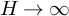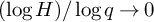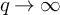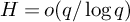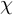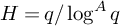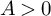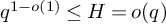1 Introduction
Let q denote a large prime, and
![]() $\chi $
a non-principal Dirichlet character modulo q. In this paper, we will be interested in the statistical behaviour of sums
$\chi $
a non-principal Dirichlet character modulo q. In this paper, we will be interested in the statistical behaviour of sums
where
![]() $H = H(q)$
is some function.
$H = H(q)$
is some function.
Since
![]() $\chi $
has period q, we may restrict attention to
$\chi $
has period q, we may restrict attention to
![]() $1 \leq H \leq q$
. The case of long sums, where
$1 \leq H \leq q$
. The case of long sums, where
![]() $H(q) \asymp q$
as
$H(q) \asymp q$
as
![]() $q \rightarrow \infty $
, has been quite extensively studied. See, for example, the work of Granville and Soundararajan [Reference Granville and Soundararajan7] and of Bober, Goldmakher, Granville and Koukoulopoulos [Reference Bober, Goldmakher, Granville and Koukoulopoulos2] investigating the largest possible values of character sums, and the recent work of Hussain [Reference Hussain12] on the behaviour of the paths
$q \rightarrow \infty $
, has been quite extensively studied. See, for example, the work of Granville and Soundararajan [Reference Granville and Soundararajan7] and of Bober, Goldmakher, Granville and Koukoulopoulos [Reference Bober, Goldmakher, Granville and Koukoulopoulos2] investigating the largest possible values of character sums, and the recent work of Hussain [Reference Hussain12] on the behaviour of the paths
![]() $t \mapsto \sum _{n \leq qt} \chi (n)$
. In this paper, we focus instead on short sums, where
$t \mapsto \sum _{n \leq qt} \chi (n)$
. In this paper, we focus instead on short sums, where
![]() $H(q) = o(q)$
as
$H(q) = o(q)$
as
![]() $q \rightarrow \infty $
. Our primary focus shall be on the situation where
$q \rightarrow \infty $
. Our primary focus shall be on the situation where
![]() $\chi $
is fixed for given q, and the start point
$\chi $
is fixed for given q, and the start point
![]() $x \in \{0,1,\ldots ,q-1\}$
varies, although we will touch on what happens when
$x \in \{0,1,\ldots ,q-1\}$
varies, although we will touch on what happens when
![]() $\chi $
varies as well.
$\chi $
varies as well.
This problem was studied by Davenport and Erdős [Reference Davenport and Erdős5], who proved that if
![]() $\chi = \left (\frac {\cdot }{q}\right )$
is the Legendre symbol, and if the function H satisfies
$\chi = \left (\frac {\cdot }{q}\right )$
is the Legendre symbol, and if the function H satisfies
![]() $H \rightarrow \infty $
but
$H \rightarrow \infty $
but
![]() $(\log H)/\log q \rightarrow 0$
as
$(\log H)/\log q \rightarrow 0$
as
![]() $q \rightarrow \infty $
, and if
$q \rightarrow \infty $
, and if
![]() $X \in \{0,1,\ldots ,q-1\}$
is uniformly random, then one has convergence in distribution to a standard Gaussian,
$X \in \{0,1,\ldots ,q-1\}$
is uniformly random, then one has convergence in distribution to a standard Gaussian,
Recall this means that for each fixed
![]() $w \in \mathbb {R}$
, we have
$w \in \mathbb {R}$
, we have
where
![]() $\Phi (w) := (1/\sqrt {2\pi }) \int _{-\infty }^{w} e^{-z^{2}/2} dz$
is the standard Gaussian cumulative distribution function. Lamzouri [Reference Lamzouri14] recently extended this to more general Dirichlet characters. He showed that if one chooses a non-real character
$\Phi (w) := (1/\sqrt {2\pi }) \int _{-\infty }^{w} e^{-z^{2}/2} dz$
is the standard Gaussian cumulative distribution function. Lamzouri [Reference Lamzouri14] recently extended this to more general Dirichlet characters. He showed that if one chooses a non-real character
![]() $\chi $
modulo each prime q (in any way), then under the same conditions on H as Davenport and Erdős [Reference Davenport and Erdős5], one has
$\chi $
modulo each prime q (in any way), then under the same conditions on H as Davenport and Erdős [Reference Davenport and Erdős5], one has
where
![]() $Z_1 , Z_2$
are independent
$Z_1 , Z_2$
are independent
![]() $N(0,1/2)$
random variables. Lamzouri [Reference Lamzouri14] also obtained a quantitative rate of convergence (in the sense of Kolmogorov distance). We also mention slightly earlier work of Mak and Zaharescu [Reference Mak and Zaharescu15], who proved separate distributional convergence results for the real and imaginary parts of
$N(0,1/2)$
random variables. Lamzouri [Reference Lamzouri14] also obtained a quantitative rate of convergence (in the sense of Kolmogorov distance). We also mention slightly earlier work of Mak and Zaharescu [Reference Mak and Zaharescu15], who proved separate distributional convergence results for the real and imaginary parts of
![]() $\frac {S_{\chi ,H}(X)}{\sqrt {H}}$
, and more generally for the projections of various kinds of moving character sum onto lines through the origin.
$\frac {S_{\chi ,H}(X)}{\sqrt {H}}$
, and more generally for the projections of various kinds of moving character sum onto lines through the origin.
All of these results, and many related ones (e.g., the work of Perret-Gentil [Reference Perret-Gentil20] on short sums of l-adic trace functions), ultimately depend on a moment method. For example, in the case
![]() $\chi = \left (\frac {\cdot }{q}\right )$
, Davenport and Erdős calculated
$\chi = \left (\frac {\cdot }{q}\right )$
, Davenport and Erdős calculated
 $$ \begin{align*}\frac{1}{q} \sum_{0 \leq x \leq q-1} \left(\frac{S_{\chi,H}(x)}{\sqrt{H}} \right)^j = \frac{1}{q H^{j/2}} \sum_{1 \leq h_1 , \ldots, h_j \leq H} \sum_{0 \leq x \leq q-1} \left(\frac{x + h_1}{q}\right) \left(\frac{x + h_2}{q}\right) ... \left(\frac{x + h_j}{q}\right) ,\end{align*} $$
$$ \begin{align*}\frac{1}{q} \sum_{0 \leq x \leq q-1} \left(\frac{S_{\chi,H}(x)}{\sqrt{H}} \right)^j = \frac{1}{q H^{j/2}} \sum_{1 \leq h_1 , \ldots, h_j \leq H} \sum_{0 \leq x \leq q-1} \left(\frac{x + h_1}{q}\right) \left(\frac{x + h_2}{q}\right) ... \left(\frac{x + h_j}{q}\right) ,\end{align*} $$
showing that for each fixed
![]() $j \in \mathbb {N}$
, this converges to the standard normal moment
$j \in \mathbb {N}$
, this converges to the standard normal moment
![]() $(1/\sqrt {2\pi }) \int _{-\infty }^{\infty } z^j e^{-z^{2}/2} dz$
as
$(1/\sqrt {2\pi }) \int _{-\infty }^{\infty } z^j e^{-z^{2}/2} dz$
as
![]() $q \rightarrow \infty $
. It is well known that the normal distribution is sufficiently nice that moment convergence implies convergence in distribution. The key to performing the moment calculation is that for a given tuple
$q \rightarrow \infty $
. It is well known that the normal distribution is sufficiently nice that moment convergence implies convergence in distribution. The key to performing the moment calculation is that for a given tuple
![]() $(h_1 , \ldots , h_j)$
of shifts, if any shift h occurs with odd multiplicity, then the sum over x is
$(h_1 , \ldots , h_j)$
of shifts, if any shift h occurs with odd multiplicity, then the sum over x is
![]() $\ll _{j} \sqrt {q}$
, by the Weil bound. Under the condition
$\ll _{j} \sqrt {q}$
, by the Weil bound. Under the condition
![]() $(\log H)/\log q \rightarrow 0$
, all these terms together give a contribution
$(\log H)/\log q \rightarrow 0$
, all these terms together give a contribution
 $$ \begin{align*}\ll_{j} \frac{1}{\sqrt{q} H^{j/2}} \sum_{\substack{1 \leq h_1 , \ldots, h_j \leq H , \\ \text{a shift occurs with odd multiplicity}}} 1 \leq \frac{H^{j/2}}{\sqrt{q}} \rightarrow 0 \quad \text{as } q \rightarrow \infty .\end{align*} $$
$$ \begin{align*}\ll_{j} \frac{1}{\sqrt{q} H^{j/2}} \sum_{\substack{1 \leq h_1 , \ldots, h_j \leq H , \\ \text{a shift occurs with odd multiplicity}}} 1 \leq \frac{H^{j/2}}{\sqrt{q}} \rightarrow 0 \quad \text{as } q \rightarrow \infty .\end{align*} $$
If one drops the condition
![]() $(\log H)/\log q \rightarrow 0$
, then this method seems to break down.
$(\log H)/\log q \rightarrow 0$
, then this method seems to break down.
Lamzouri [Reference Lamzouri14] made the following conjecture about what happens for larger H.
Conjecture 1 (Lamzouri, 2013).
Suppose that
![]() $H \rightarrow \infty $
but
$H \rightarrow \infty $
but
![]() $H = o(q/\log q)$
as the prime
$H = o(q/\log q)$
as the prime
![]() $q \rightarrow \infty $
. Then if
$q \rightarrow \infty $
. Then if
![]() $\chi = \left (\frac {\cdot }{q}\right )$
is the Legendre symbol, and if
$\chi = \left (\frac {\cdot }{q}\right )$
is the Legendre symbol, and if
![]() $X \in \{0,1,\ldots ,q-1\}$
is uniformly random, we have
$X \in \{0,1,\ldots ,q-1\}$
is uniformly random, we have
If we choose a non-real character
![]() $\chi $
modulo each prime q (in any way), then on the same range of H we have
$\chi $
modulo each prime q (in any way), then on the same range of H we have
where
![]() $Z_1 , Z_2$
are independent
$Z_1 , Z_2$
are independent
![]() $N(0,1/2)$
random variables.
$N(0,1/2)$
random variables.
Our goal here is the further investigation of Lamzouri’s conjecture. Prior to this, we briefly explain the origins of the conjecture, and in particular of the condition
![]() $H = o(q/\log q)$
. For each prime p, let
$H = o(q/\log q)$
. For each prime p, let
![]() $f(p)$
be an independent random variable taking values
$f(p)$
be an independent random variable taking values
![]() $\pm 1$
with probability 1/2 each (i.e., a Rademacher random variable), and then for each
$\pm 1$
with probability 1/2 each (i.e., a Rademacher random variable), and then for each
![]() $n \in \mathbb {N}$
, define
$n \in \mathbb {N}$
, define
 $$ \begin{align*}f(n) := \prod_{p^{\alpha} ||n} f(p)^{\alpha} ,\end{align*} $$
$$ \begin{align*}f(n) := \prod_{p^{\alpha} ||n} f(p)^{\alpha} ,\end{align*} $$
where
![]() $p^{\alpha } ||n$
means that
$p^{\alpha } ||n$
means that
![]() $p^{\alpha }$
is the highest power of p that divides n. We shall refer to such f as an extended Rademacher random multiplicative function and think of f as a random model for the Legendre symbol
$p^{\alpha }$
is the highest power of p that divides n. We shall refer to such f as an extended Rademacher random multiplicative function and think of f as a random model for the Legendre symbol
![]() $\left (\frac {n}{q}\right )$
as q varies. Similarly, to model a complex Dirichlet character
$\left (\frac {n}{q}\right )$
as q varies. Similarly, to model a complex Dirichlet character
![]() $\chi (n)$
, we let
$\chi (n)$
, we let
![]() $f(p)$
be uniformly distributed on the complex unit circle (i.e., Steinhaus random variables) and again define
$f(p)$
be uniformly distributed on the complex unit circle (i.e., Steinhaus random variables) and again define
![]() $f(n) := \prod _{p^{\alpha } ||n} f(p)^{\alpha }$
, a Steinhaus random multiplicative function. Chatterjee and Soundararajan [Reference Chatterjee and Soundararajan4] showed that for a very similarFootnote
1
kind of real random function f, one has
$f(n) := \prod _{p^{\alpha } ||n} f(p)^{\alpha }$
, a Steinhaus random multiplicative function. Chatterjee and Soundararajan [Reference Chatterjee and Soundararajan4] showed that for a very similarFootnote
1
kind of real random function f, one has
 $$ \begin{align*}\frac{\sum_{x < n \leq x+y} f(n)}{\sqrt{\mathbb{E} \left(\sum_{x < n \leq x+y} f(n) \right)^2 }} \stackrel{d}{\rightarrow} N(0,1) \quad \text{as } x \rightarrow \infty\end{align*} $$
$$ \begin{align*}\frac{\sum_{x < n \leq x+y} f(n)}{\sqrt{\mathbb{E} \left(\sum_{x < n \leq x+y} f(n) \right)^2 }} \stackrel{d}{\rightarrow} N(0,1) \quad \text{as } x \rightarrow \infty\end{align*} $$
provided the interval length
![]() $y=y(x)$
satisfies
$y=y(x)$
satisfies
![]() $x^{1/5}\log x \ll y = o(x/\log x)$
. Lamzouri’s conjectured condition
$x^{1/5}\log x \ll y = o(x/\log x)$
. Lamzouri’s conjectured condition
![]() $H = o(q/\log q)$
is analogous to Chatterjee and Soundararajan’s upper bound on y.
$H = o(q/\log q)$
is analogous to Chatterjee and Soundararajan’s upper bound on y.
There are at least two issues that need to be understood when considering whether the random multiplicative model is a good one for
![]() $S_{\chi ,H}(X)$
. The first is whether a random multiplicative function captures all of the important structure of a Dirichlet character, which in particular has an additional periodicity property. The second is whether one can infer things about
$S_{\chi ,H}(X)$
. The first is whether a random multiplicative function captures all of the important structure of a Dirichlet character, which in particular has an additional periodicity property. The second is whether one can infer things about
![]() $S_{\chi ,H}(X)$
, where the function
$S_{\chi ,H}(X)$
, where the function
![]() $\chi $
is fixed (for given q) and the start point X of the interval randomly varies, from things about
$\chi $
is fixed (for given q) and the start point X of the interval randomly varies, from things about
![]() $\sum _{x < n \leq x+y} f(n)$
where the interval is fixed (for given x) and the function f randomly varies. One might think that if the latter is a good model for character sums, it would rather be for the case of a fixed interval for given q and randomly varying character
$\sum _{x < n \leq x+y} f(n)$
where the interval is fixed (for given x) and the function f randomly varies. One might think that if the latter is a good model for character sums, it would rather be for the case of a fixed interval for given q and randomly varying character
![]() $\chi $
mod q.
$\chi $
mod q.
1.1 Statement of results
Our main results are negative, showing that Conjecture 1 is not correct as stated.
Theorem 1. Let
![]() $A> 0$
be arbitrary but fixed, and set
$A> 0$
be arbitrary but fixed, and set
![]() $H(q) = q/\log ^{A}q$
. Then as q varies over all large primes, with
$H(q) = q/\log ^{A}q$
. Then as q varies over all large primes, with
![]() $\chi = \left (\frac {\cdot }{q}\right )$
denoting the unique corresponding quadratic character, we have
$\chi = \left (\frac {\cdot }{q}\right )$
denoting the unique corresponding quadratic character, we have
Theorem 2. Let
![]() $A> 0$
be arbitrary but fixed, and set
$A> 0$
be arbitrary but fixed, and set
![]() $H(q) = q/\log ^{A}q$
. Then as q varies over all large primes, there exists a corresponding sequence of non-real characters
$H(q) = q/\log ^{A}q$
. Then as q varies over all large primes, there exists a corresponding sequence of non-real characters
![]() $\chi $
modulo q for which
$\chi $
modulo q for which
where
![]() $Z_1 , Z_2$
are independent
$Z_1 , Z_2$
are independent
![]() $N(0,1/2)$
random variables.
$N(0,1/2)$
random variables.
It may not be very illuminating just to say that something does not converge to a specified limit object. In fact, in the real case covered by Theorem 1, we will show that there exists an infinite sequence of primes q along which
![]() $\frac {S_{\chi ,H}(X)}{\sqrt {H}}$
has properties that forbid it from closely approaching the
$\frac {S_{\chi ,H}(X)}{\sqrt {H}}$
has properties that forbid it from closely approaching the
![]() $N(0,1)$
limit. This special sequence consists of primes q for which
$N(0,1)$
limit. This special sequence consists of primes q for which
![]() $\left (\frac {\cdot }{q}\right )$
is ‘highly biased’, in the sense that its partial sums up to about
$\left (\frac {\cdot }{q}\right )$
is ‘highly biased’, in the sense that its partial sums up to about
![]() $q/H$
are not small. Similarly, in the non-real case covered by Theorem 2, the bad character
$q/H$
are not small. Similarly, in the non-real case covered by Theorem 2, the bad character
![]() $\chi $
that we select for each prime q is such that its partial sum up to about
$\chi $
that we select for each prime q is such that its partial sum up to about
![]() $q/H$
has large modulus.
$q/H$
has large modulus.
To explain further, if
![]() $\chi $
is primitive mod q (so for q prime, any non-principal character is admissible), then Pólya’s Fourier expansion for character sums implies that
$\chi $
is primitive mod q (so for q prime, any non-principal character is admissible), then Pólya’s Fourier expansion for character sums implies that
 $$ \begin{align*}S_{\chi, H}(x) = \frac{\tau(\chi)}{2\pi i} \sum_{0 < |k| < q/2} \frac{\overline{\chi}(-k)}{k} e(kx/q) (e(kH/q) - 1) + O(\log q) .\end{align*} $$
$$ \begin{align*}S_{\chi, H}(x) = \frac{\tau(\chi)}{2\pi i} \sum_{0 < |k| < q/2} \frac{\overline{\chi}(-k)}{k} e(kx/q) (e(kH/q) - 1) + O(\log q) .\end{align*} $$
Here,
![]() $\tau (\chi )$
denotes the Gauss sum, of absolute value
$\tau (\chi )$
denotes the Gauss sum, of absolute value
![]() $\sqrt {q}$
, and
$\sqrt {q}$
, and
![]() $e(\cdot ) = e^{2\pi i \cdot }$
denotes the complex exponential. When
$e(\cdot ) = e^{2\pi i \cdot }$
denotes the complex exponential. When
![]() $|k| \leq q/H$
, we have
$|k| \leq q/H$
, we have
![]() $(1/k) (e(kH/q) - 1) \approx 2\pi i (H/q)$
, and it turns out that (on average over x) these are essentially the only terms that make a significant contribution, so
$(1/k) (e(kH/q) - 1) \approx 2\pi i (H/q)$
, and it turns out that (on average over x) these are essentially the only terms that make a significant contribution, so
 $$ \begin{align} \frac{S_{\chi, H}(x)}{\sqrt{H}} \approx \frac{\tau(\chi)\sqrt{H}}{q} \sum_{0 < |k| < q/H} \overline{\chi}(-k) e(kx/q). \end{align} $$
$$ \begin{align} \frac{S_{\chi, H}(x)}{\sqrt{H}} \approx \frac{\tau(\chi)\sqrt{H}}{q} \sum_{0 < |k| < q/H} \overline{\chi}(-k) e(kx/q). \end{align} $$
Now if
![]() $H = q/\log ^{A}q$
, and so
$H = q/\log ^{A}q$
, and so
![]() $q/H = \log ^{A}q$
, we can find characters
$q/H = \log ^{A}q$
, we can find characters
![]() $\chi $
for which
$\chi $
for which
![]() $|\sum _{0 < k < q/H} \chi (k)| \gg _{A} q/H$
. For such characters, we can think of
$|\sum _{0 < k < q/H} \chi (k)| \gg _{A} q/H$
. For such characters, we can think of
![]() $S_{\chi , H}(x)/\sqrt {H}$
as having a significant piece resembling the scaled Dirichlet kernel
$S_{\chi , H}(x)/\sqrt {H}$
as having a significant piece resembling the scaled Dirichlet kernel
![]() $(\tau (\chi )\sqrt {H}/q) \sum _{0 < |k| < q/H} e(kx/q)$
. The Dirichlet kernel certainly does not have Gaussian behaviour as x varies and
$(\tau (\chi )\sqrt {H}/q) \sum _{0 < |k| < q/H} e(kx/q)$
. The Dirichlet kernel certainly does not have Gaussian behaviour as x varies and
![]() $q \rightarrow \infty $
; in fact (since it has relatively small
$q \rightarrow \infty $
; in fact (since it has relatively small
![]() $L^{1}$
norm), it converges to 0 in probability, which suggests it is unlikely that
$L^{1}$
norm), it converges to 0 in probability, which suggests it is unlikely that
![]() $S_{\chi , H}(x)/\sqrt {H}$
can converge to the desired Gaussian. This argument can be made rigorous by subtracting a suitable multiple of the Dirichlet kernel from
$S_{\chi , H}(x)/\sqrt {H}$
can converge to the desired Gaussian. This argument can be made rigorous by subtracting a suitable multiple of the Dirichlet kernel from
![]() $S_{\chi , H}(x)/\sqrt {H}$
, which makes no difference to the putative convergence in distribution but reduces the variance of the sum.
$S_{\chi , H}(x)/\sqrt {H}$
, which makes no difference to the putative convergence in distribution but reduces the variance of the sum.
Note that the use of Pólya’s Fourier expansion imports information about the periodicity of
![]() $\chi $
mod q into our analysis.
$\chi $
mod q into our analysis.
The characters used in the proofs of Theorems 1 and 2 are quite special, suggesting that Lamzouri’s conjecture might be true for almost all q for real characters, or for almost all characters for each q for non-real characters. Another reason for believing this comes from thinking more carefully about the representation (1.1). In a famous classical paper, Salem and Zygmund [Reference Salem and Zygmund21] showed that for almost all sequences of independent
![]() $\pm 1$
coefficients, the partial Fourier series with those coefficients satisfy a central limit theorem when the ‘frequency’ (corresponding to
$\pm 1$
coefficients, the partial Fourier series with those coefficients satisfy a central limit theorem when the ‘frequency’ (corresponding to
![]() $x/q$
in our setup) is chosen uniformly at random. Thus, if we believe that the values of a typical Dirichlet character are somewhat ‘random looking’, we might expect to have a central limit theorem as the length
$x/q$
in our setup) is chosen uniformly at random. Thus, if we believe that the values of a typical Dirichlet character are somewhat ‘random looking’, we might expect to have a central limit theorem as the length
![]() $q/H$
tends to infinity. This translates into a condition
$q/H$
tends to infinity. This translates into a condition
![]() $H = o(q)$
rather than the condition
$H = o(q)$
rather than the condition
![]() $H = o(q/\log q)$
proposed by Lamzouri [Reference Lamzouri14].
$H = o(q/\log q)$
proposed by Lamzouri [Reference Lamzouri14].
In this positive ‘almost all’ direction, we establish the following.
Theorem 3. Let
![]() $H = H(q)$
satisfy
$H = H(q)$
satisfy
![]() $\frac {\log (q/H)}{\log q} \rightarrow 0$
and
$\frac {\log (q/H)}{\log q} \rightarrow 0$
and
![]() $H = o(q)$
as the prime
$H = o(q)$
as the prime
![]() $q \rightarrow \infty $
. Then there exists a subset
$q \rightarrow \infty $
. Then there exists a subset
![]() $\mathcal {P}_{H}$
of primes, which satisfies
$\mathcal {P}_{H}$
of primes, which satisfies
 $$ \begin{align*}\frac{\#(\mathcal{P}_{H} \cap [Q,2Q])}{\#\{ Q \leq q \leq 2Q : \; q \; \text{prime}\}} \geq 1 - O(e^{-\min_{Q \leq q \leq 2Q}\log^{3/4}(q/H)})\end{align*} $$
$$ \begin{align*}\frac{\#(\mathcal{P}_{H} \cap [Q,2Q])}{\#\{ Q \leq q \leq 2Q : \; q \; \text{prime}\}} \geq 1 - O(e^{-\min_{Q \leq q \leq 2Q}\log^{3/4}(q/H)})\end{align*} $$
(say) for all
![]() $Q = 2^j, j \in \mathbb {N}$
, such that if
$Q = 2^j, j \in \mathbb {N}$
, such that if
![]() $\chi = \left (\frac {\cdot }{q}\right )$
, we have
$\chi = \left (\frac {\cdot }{q}\right )$
, we have
Theorem 4. Let
![]() $H = H(q)$
satisfy
$H = H(q)$
satisfy
![]() $\frac {\log (q/H)}{\log q} \rightarrow 0$
and
$\frac {\log (q/H)}{\log q} \rightarrow 0$
and
![]() $H = o(q)$
as the prime
$H = o(q)$
as the prime
![]() $q \rightarrow \infty $
. Then there exist sets
$q \rightarrow \infty $
. Then there exist sets
![]() $\mathcal {G}_{q, H}$
of characters mod q, satisfying
$\mathcal {G}_{q, H}$
of characters mod q, satisfying
![]() $\#\mathcal {G}_{q,H} \geq q(1 - O(e^{-\log ^{3/4}(q/H)}))$
, such that for any choice of
$\#\mathcal {G}_{q,H} \geq q(1 - O(e^{-\log ^{3/4}(q/H)}))$
, such that for any choice of
![]() $\chi \in \mathcal {G}_{q, H}$
, we have
$\chi \in \mathcal {G}_{q, H}$
, we have
where
![]() $Z_1 , Z_2$
are independent
$Z_1 , Z_2$
are independent
![]() $N(0,1/2)$
random variables.
$N(0,1/2)$
random variables.
The proofs of Theorems 3 and 4 again use the trigonometric series approximation to
![]() $S_{\chi , H}(x)/\sqrt {H}$
, which can be reworked slightly into a form (roughly speaking) like
$S_{\chi , H}(x)/\sqrt {H}$
, which can be reworked slightly into a form (roughly speaking) like
 $$ \begin{align} \frac{S_{\chi, H}(x)}{\sqrt{H}} \approx \frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{0 < k < q/H} \frac{\overline{\chi}(k) \sin(\pi k H/q)}{k} \cos(2 \pi k x/q). \end{align} $$
$$ \begin{align} \frac{S_{\chi, H}(x)}{\sqrt{H}} \approx \frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{0 < k < q/H} \frac{\overline{\chi}(k) \sin(\pi k H/q)}{k} \cos(2 \pi k x/q). \end{align} $$
In fact, looking at
![]() $S_{\chi , H}(X)/\sqrt {H}$
for
$S_{\chi , H}(X)/\sqrt {H}$
for
![]() $X \in \{0,1,\ldots ,q-1\}$
uniformly random turns out to be roughly equivalent to looking at
$X \in \{0,1,\ldots ,q-1\}$
uniformly random turns out to be roughly equivalent to looking at
![]() $\frac {2\sqrt {q}}{\pi \sqrt {H}} \sum _{0 < k < q/H} \frac {\overline {\chi }(k) \sin (\pi k H/q)}{k} \cos (2 \pi k \theta )$
, for
$\frac {2\sqrt {q}}{\pi \sqrt {H}} \sum _{0 < k < q/H} \frac {\overline {\chi }(k) \sin (\pi k H/q)}{k} \cos (2 \pi k \theta )$
, for
![]() $\theta \in [0,1]$
uniformly random. This latter small change is not really important, but neatens the writing.
$\theta \in [0,1]$
uniformly random. This latter small change is not really important, but neatens the writing.
Since moment convergence implies distributional convergence to the Gaussian, to prove Theorem 3, it would suffice (roughly speaking) to show the existence of a subsequence
![]() $\mathcal {P}_H$
of primes such that, for each fixed
$\mathcal {P}_H$
of primes such that, for each fixed
![]() $j \in \mathbb {N}$
, we have
$j \in \mathbb {N}$
, we have
 $$ \begin{align*}\int_{0}^{1} \left( \frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{1 \leq k < q/H} \frac{\left(\frac{k}{q}\right) \sin(\pi k H/q)}{k} \cos(2\pi k\theta) \right)^{j} d\theta \rightarrow (1/\sqrt{2\pi}) \int_{-\infty}^{\infty} z^j e^{-z^{2}/2} dz\end{align*} $$
$$ \begin{align*}\int_{0}^{1} \left( \frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{1 \leq k < q/H} \frac{\left(\frac{k}{q}\right) \sin(\pi k H/q)}{k} \cos(2\pi k\theta) \right)^{j} d\theta \rightarrow (1/\sqrt{2\pi}) \int_{-\infty}^{\infty} z^j e^{-z^{2}/2} dz\end{align*} $$
as
![]() $q \rightarrow \infty , q \in \mathcal {P}_{H}$
. To do this, we can try to calculate the average (square) discrepancy between the actual and the Gaussian moments as q varies in each dyadic interval – namely,
$q \rightarrow \infty , q \in \mathcal {P}_{H}$
. To do this, we can try to calculate the average (square) discrepancy between the actual and the Gaussian moments as q varies in each dyadic interval – namely,
 $$ \begin{align*}& \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{prime}}} \\ &\quad \times\left| \int_{0}^{1} \left( \frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{1 \leq k < q/H} \frac{\left(\frac{k}{q}\right) \sin(\pi k H/q)}{k} \cos(2\pi k\theta) \right)^{j} d\theta - \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} z^j e^{-z^{2}/2} dz \right|^2 .\end{align*} $$
$$ \begin{align*}& \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{prime}}} \\ &\quad \times\left| \int_{0}^{1} \left( \frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{1 \leq k < q/H} \frac{\left(\frac{k}{q}\right) \sin(\pi k H/q)}{k} \cos(2\pi k\theta) \right)^{j} d\theta - \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} z^j e^{-z^{2}/2} dz \right|^2 .\end{align*} $$
If this tends to zero at a sufficient rate as
![]() $Q \rightarrow \infty $
, on a range of j that grows to infinity as
$Q \rightarrow \infty $
, on a range of j that grows to infinity as
![]() $Q \rightarrow \infty $
(recall that we need convergence of all fixed integer moments to guarantee convergence to the Gaussian), then we can form
$Q \rightarrow \infty $
(recall that we need convergence of all fixed integer moments to guarantee convergence to the Gaussian), then we can form
![]() $\mathcal {P}_H$
from all the many primes in each interval
$\mathcal {P}_H$
from all the many primes in each interval
![]() $[Q,2Q]$
where the discrepancy is simultaneously small for a suitable range of j.
$[Q,2Q]$
where the discrepancy is simultaneously small for a suitable range of j.
Provided that
![]() $(q/H)^j$
is small compared with Q, so the periodicity of the characters
$(q/H)^j$
is small compared with Q, so the periodicity of the characters
![]() $\left (\frac {k}{q}\right )$
does not intervene, one expects the left-hand side in the above display to be close to the corresponding one where
$\left (\frac {k}{q}\right )$
does not intervene, one expects the left-hand side in the above display to be close to the corresponding one where
![]() $\left (\frac {k}{q}\right )$
is replaced by an extended Rademacher random multiplicative function
$\left (\frac {k}{q}\right )$
is replaced by an extended Rademacher random multiplicative function
![]() $f(k)$
, and the normalised sum
$f(k)$
, and the normalised sum
![]() $\frac {\log Q}{Q} \sum _{\substack {Q \leq q \leq 2Q, \\ q \; \text {prime}}}$
is replaced by an expectation
$\frac {\log Q}{Q} \sum _{\substack {Q \leq q \leq 2Q, \\ q \; \text {prime}}}$
is replaced by an expectation
![]() $\mathbb {E}$
. There are technical challenges in establishing this because
$\mathbb {E}$
. There are technical challenges in establishing this because
![]() $q/H(q)$
might also vary with q in the sum, and averaging over primes q entails non-trivial issues with the distribution of primes, but these problems can be overcome (see Number Theory Result 3 and Section 6.3 below; essentially one needs to show that the
$q/H(q)$
might also vary with q in the sum, and averaging over primes q entails non-trivial issues with the distribution of primes, but these problems can be overcome (see Number Theory Result 3 and Section 6.3 below; essentially one needs to show that the
![]() $\left (\frac {k}{q}\right )$
for varying q have similar correlation/orthogonality properties to the random
$\left (\frac {k}{q}\right )$
for varying q have similar correlation/orthogonality properties to the random
![]() $f(k)$
). Unfortunately, the condition that
$f(k)$
). Unfortunately, the condition that
![]() $(q/H)^j$
is small compared with Q, for each fixed j, forces the unwanted condition
$(q/H)^j$
is small compared with Q, for each fixed j, forces the unwanted condition
![]() $\frac {\log (q/H)}{\log q} \rightarrow 0$
in Theorem 3. This is similar to the condition
$\frac {\log (q/H)}{\log q} \rightarrow 0$
in Theorem 3. This is similar to the condition
![]() $(\log H)/\log q \rightarrow 0$
that appeared in the work of Davenport and Erdős [Reference Davenport and Erdős5], Lamzouri [Reference Lamzouri14] and others.
$(\log H)/\log q \rightarrow 0$
that appeared in the work of Davenport and Erdős [Reference Davenport and Erdős5], Lamzouri [Reference Lamzouri14] and others.
Finally, we need upper bounds for quantities like
 $$ \begin{align*}\mathbb{E} \left| \int_{0}^{1} \left( \frac{2\sqrt{Q}}{\pi \sqrt{H}} \sum_{1 \leq k < Q/H} \frac{f(k) \sin(\pi k H/Q)}{k} \cos(2\pi k\theta) \right)^{j} d\theta - \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} z^j e^{-z^{2}/2} dz \right|^2 ,\end{align*} $$
$$ \begin{align*}\mathbb{E} \left| \int_{0}^{1} \left( \frac{2\sqrt{Q}}{\pi \sqrt{H}} \sum_{1 \leq k < Q/H} \frac{f(k) \sin(\pi k H/Q)}{k} \cos(2\pi k\theta) \right)^{j} d\theta - \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} z^j e^{-z^{2}/2} dz \right|^2 ,\end{align*} $$
where
![]() $f(k)$
is a random multiplicative function. This arithmetic input can be extracted from a nice recent paper of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1]. They were interested in almost sure central limit theorems and size bounds for random trigonometric polynomials
$f(k)$
is a random multiplicative function. This arithmetic input can be extracted from a nice recent paper of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1]. They were interested in almost sure central limit theorems and size bounds for random trigonometric polynomials
![]() $\frac {1}{\sqrt {N}} \sum _{n \leq N} f(n) e(n\theta )$
and directly calculated such expectations using a point counting argument drawing on work of Vaughan and Wooley [Reference Vaughan and Wooley23]. Ultimately, one needs to count tuples
$\frac {1}{\sqrt {N}} \sum _{n \leq N} f(n) e(n\theta )$
and directly calculated such expectations using a point counting argument drawing on work of Vaughan and Wooley [Reference Vaughan and Wooley23]. Ultimately, one needs to count tuples
![]() $(n_1, \ldots , n_{2j})$
satisfying a small collection of linear and multiplicative equations.
$(n_1, \ldots , n_{2j})$
satisfying a small collection of linear and multiplicative equations.
As Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1] comment, one can also analyse the distribution of
![]() $\frac {1}{\sqrt {N}} \sum _{n \leq N} f(n) e(n\theta )$
using martingale methods, and this was done in unpublished work of the present author (see the paper [Reference Harper9] for an application of martingales to a different distributional problem for random multiplicative functions, and the recent paper [Reference Soundararajan and Xu22] of Soundararajan and Xu for various such applications, including to trigonometric polynomials with random multiplicative coefficients). But to transfer these conclusions to character sums, one would seem to again need moment estimates on the random multiplicative side, not just distributional convergence. These could be obtained (e.g., one can use Burkholder’s inequalities [Reference Burkholder3] and some calculation to show that all moments remain bounded as
$\frac {1}{\sqrt {N}} \sum _{n \leq N} f(n) e(n\theta )$
using martingale methods, and this was done in unpublished work of the present author (see the paper [Reference Harper9] for an application of martingales to a different distributional problem for random multiplicative functions, and the recent paper [Reference Soundararajan and Xu22] of Soundararajan and Xu for various such applications, including to trigonometric polynomials with random multiplicative coefficients). But to transfer these conclusions to character sums, one would seem to again need moment estimates on the random multiplicative side, not just distributional convergence. These could be obtained (e.g., one can use Burkholder’s inequalities [Reference Burkholder3] and some calculation to show that all moments remain bounded as
![]() $N \rightarrow \infty $
, and this combined with distributional convergence implies they must all converge to the desired Gaussian moments), but it seems simpler to rely on the existing calculations of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1].
$N \rightarrow \infty $
, and this combined with distributional convergence implies they must all converge to the desired Gaussian moments), but it seems simpler to rely on the existing calculations of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1].
In the complex case in Theorem 4, one proceeds exactly similarly in studying the square discrepancy from the moments of the complex Gaussian
![]() $Z_1 + iZ_2$
, now averaging over all
$Z_1 + iZ_2$
, now averaging over all
![]() $\chi $
mod q rather than over
$\chi $
mod q rather than over
![]() $Q \leq q \leq 2Q$
. Provided that
$Q \leq q \leq 2Q$
. Provided that
![]() $1 \leq n_1, n_2 < q$
, say, we have the identity
$1 \leq n_1, n_2 < q$
, say, we have the identity
![]() $\frac {1}{q-1} \sum _{\chi \; \text {mod} \; q} \chi (n_1) \overline {\chi }(n_2) = \textbf {1}_{n_1 \equiv n_2 \; \text {mod} \; q} = \textbf {1}_{n_1 = n_2} = \mathbb {E} f(n_1) \overline {f}(n_2)$
, where
$\frac {1}{q-1} \sum _{\chi \; \text {mod} \; q} \chi (n_1) \overline {\chi }(n_2) = \textbf {1}_{n_1 \equiv n_2 \; \text {mod} \; q} = \textbf {1}_{n_1 = n_2} = \mathbb {E} f(n_1) \overline {f}(n_2)$
, where
![]() $f(\cdot )$
denotes a Steinhaus random multiplicative function. This exact equality makes it much easier to establish the connection with random multiplicative functions than in Theorem 3, but the condition
$f(\cdot )$
denotes a Steinhaus random multiplicative function. This exact equality makes it much easier to establish the connection with random multiplicative functions than in Theorem 3, but the condition
![]() $1 \leq n_1, n_2 < q$
ultimately forces the same unwanted constraint
$1 \leq n_1, n_2 < q$
ultimately forces the same unwanted constraint
![]() $\frac {\log (q/H)}{\log q} \rightarrow 0$
.
$\frac {\log (q/H)}{\log q} \rightarrow 0$
.
1.2 Discussion and open questions
Our results leave open several problems about the behaviour of
![]() $S_{\chi , H}(x)/\sqrt {H}$
, and related issues.
$S_{\chi , H}(x)/\sqrt {H}$
, and related issues.
The results of Davenport and Erdős [Reference Davenport and Erdős5] and of Lamzouri [Reference Lamzouri14] establish a central limit theorem for all characters provided
![]() $H \rightarrow \infty $
but
$H \rightarrow \infty $
but
![]() $H = q^{o(1)}$
, and our results establish a central limit theorem for almost all characters provided
$H = q^{o(1)}$
, and our results establish a central limit theorem for almost all characters provided
![]() $q^{1-o(1)} \leq H = o(q)$
. Moreover, we have shown that one cannot hope to prove a central limit theorem for all characters when
$q^{1-o(1)} \leq H = o(q)$
. Moreover, we have shown that one cannot hope to prove a central limit theorem for all characters when
![]() $\log (q/H)/\log \log q$
is bounded. Given this state of affairs, one can ask the following:
$\log (q/H)/\log \log q$
is bounded. Given this state of affairs, one can ask the following:
-
(i) How does
 $S_{\chi , H}(x)/\sqrt {H}$
behave on the missing range
$S_{\chi , H}(x)/\sqrt {H}$
behave on the missing range
 $q^{o(1)} \leq H \leq q^{1-o(1)}$
?
$q^{o(1)} \leq H \leq q^{1-o(1)}$
? -
(ii) Indeed, should it be possible to prove a central limit theorem for all characters provided
 $H \rightarrow \infty $
and
$H \rightarrow \infty $
and
 $\log (q/H)/\log \log q \rightarrow \infty $
?
$\log (q/H)/\log \log q \rightarrow \infty $
?
The author tentatively conjectures that the answer to (ii) is Yes. In view of Corollary A of Granville and Soundararajan [Reference Granville and Soundararajan6], if the Generalised Riemann Hypothesis is true, then
![]() $\sum _{n \leq x} \chi (n) = o(x)$
whenever
$\sum _{n \leq x} \chi (n) = o(x)$
whenever
![]() $\chi $
is a non-principal character mod q, and
$\chi $
is a non-principal character mod q, and
![]() $(\log x)/\log \log q \rightarrow \infty $
. This means that, assuming GRH, there would be no construction along the lines of Theorems 1 and 2 available once
$(\log x)/\log \log q \rightarrow \infty $
. This means that, assuming GRH, there would be no construction along the lines of Theorems 1 and 2 available once
![]() $\log (q/H)/\log \log q \rightarrow \infty $
. So if one believes this is the only barrier to a central limit theorem holding, as is somewhat suggested by the representation (1.1) together with the classical work of Salem and Zygmund [Reference Salem and Zygmund21] on random Fourier series, then one arrives at this conjecture.
$\log (q/H)/\log \log q \rightarrow \infty $
. So if one believes this is the only barrier to a central limit theorem holding, as is somewhat suggested by the representation (1.1) together with the classical work of Salem and Zygmund [Reference Salem and Zygmund21] on random Fourier series, then one arrives at this conjecture.
However, proving such a result seems difficult. First, the best unconditional estimates we have of the form
![]() $\sum _{n \leq x} \chi (n) = o(x)$
, where
$\sum _{n \leq x} \chi (n) = o(x)$
, where
![]() $\chi $
is any non-principal character modulo a prime q (one can sometimes do better for special non-prime moduli), are Burgess-type estimates requiring that
$\chi $
is any non-principal character modulo a prime q (one can sometimes do better for special non-prime moduli), are Burgess-type estimates requiring that
![]() $x \geq q^{1/4 - o(1)}$
. Thus, we would need to assume results like GRH merely to exclude the kind of construction from Theorems 1 and 2 from cropping up. But even allowing such unproved arithmetical results, there is no clear way to go on and establish a central limit theorem on the full range of H in (ii). The problem of understanding the distribution of
$x \geq q^{1/4 - o(1)}$
. Thus, we would need to assume results like GRH merely to exclude the kind of construction from Theorems 1 and 2 from cropping up. But even allowing such unproved arithmetical results, there is no clear way to go on and establish a central limit theorem on the full range of H in (ii). The problem of understanding the distribution of
![]() $(\tau (\chi )\sqrt {H}/q) \sum _{0 < |k| < q/H} \overline {\chi }(-k) e(k\theta )$
, where
$(\tau (\chi )\sqrt {H}/q) \sum _{0 < |k| < q/H} \overline {\chi }(-k) e(k\theta )$
, where
![]() $\theta = X/q$
is random but the coefficients
$\theta = X/q$
is random but the coefficients
![]() $\overline {\chi }(-k)$
are deterministic, is just one example of the important general problem of understanding the distribution of
$\overline {\chi }(-k)$
are deterministic, is just one example of the important general problem of understanding the distribution of
![]() $\sum _{k} a_k e(k\theta )$
, where
$\sum _{k} a_k e(k\theta )$
, where
![]() $a_k$
are interesting deterministic coefficients. See, for example, the work of Hughes and Rudnick [Reference Hughes and Rudnick11] on lattice points in annuli. They encounter similar sums where the
$a_k$
are interesting deterministic coefficients. See, for example, the work of Hughes and Rudnick [Reference Hughes and Rudnick11] on lattice points in annuli. They encounter similar sums where the
![]() $a_k$
involve the number of representations of k as a sum of two squares, and the range of their main theorem involves a similar (conjecturally unnecessary) restriction as in Theorems 3 and 4 to allow a proof by the method of moments.
$a_k$
involve the number of representations of k as a sum of two squares, and the range of their main theorem involves a similar (conjecturally unnecessary) restriction as in Theorems 3 and 4 to allow a proof by the method of moments.
Indeed, even extending our ‘almost all’ results to a wider range of H would be very interesting, and does not seem easily attackable.
Another, perhaps rather specialised, question is the following:
-
(iii) What can be said about the distribution of
 $S_{\chi , H}(X)/\sqrt {H}$
, for those characters
$S_{\chi , H}(X)/\sqrt {H}$
, for those characters
 $\chi $
and interval lengths H where it does not satisfy the expected central limit theorem?
$\chi $
and interval lengths H where it does not satisfy the expected central limit theorem?
We can also return to the random multiplicative functions
![]() $f(n)$
that motivated Lamzouri’s conjecture [Reference Lamzouri14] and played a role in the proofs of Theorems 3 and 4. As discussed earlier, and perhaps demonstrated by Theorems 1 and 2, the author does not believe that Chatterjee and Soundararajan’s work [Reference Chatterjee and Soundararajan4] on
$f(n)$
that motivated Lamzouri’s conjecture [Reference Lamzouri14] and played a role in the proofs of Theorems 3 and 4. As discussed earlier, and perhaps demonstrated by Theorems 1 and 2, the author does not believe that Chatterjee and Soundararajan’s work [Reference Chatterjee and Soundararajan4] on
![]() $\sum _{x < n \leq x+y} f(n)$
provides a natural model for
$\sum _{x < n \leq x+y} f(n)$
provides a natural model for
![]() $S_{\chi , H}(X)$
. But the study of
$S_{\chi , H}(X)$
. But the study of
![]() $\sum _{x < n \leq x+y} f(n)$
is very interesting in its own right. Although Chatterjee and Soundararajan only obtainedFootnote
2
a Gaussian limiting distribution when
$\sum _{x < n \leq x+y} f(n)$
is very interesting in its own right. Although Chatterjee and Soundararajan only obtainedFootnote
2
a Gaussian limiting distribution when
![]() $x^{1/5}\log x \ll y = o(x/\log x)$
, they did not show that their upper bound on y is optimal, and recent work of Soundararajan and Xu [Reference Soundararajan and Xu22] extends the range to
$x^{1/5}\log x \ll y = o(x/\log x)$
, they did not show that their upper bound on y is optimal, and recent work of Soundararajan and Xu [Reference Soundararajan and Xu22] extends the range to
However, it follows directly from work of the author [Reference Harper10] that if
![]() $\frac {y \sqrt {\log \log x}}{x} \rightarrow \infty $
as
$\frac {y \sqrt {\log \log x}}{x} \rightarrow \infty $
as
![]() $x \rightarrow \infty $
, then
$x \rightarrow \infty $
, then
 $$ \begin{align*}\frac{\mathbb{E}|\sum_{x < n \leq x+y} f(n)|}{\sqrt{y}} \leq \frac{\mathbb{E}|\sum_{n \leq x} f(n)| + \mathbb{E}|\sum_{n \leq x+y} f(n)|}{\sqrt{y}} \rightarrow 0 .\end{align*} $$
$$ \begin{align*}\frac{\mathbb{E}|\sum_{x < n \leq x+y} f(n)|}{\sqrt{y}} \leq \frac{\mathbb{E}|\sum_{n \leq x} f(n)| + \mathbb{E}|\sum_{n \leq x+y} f(n)|}{\sqrt{y}} \rightarrow 0 .\end{align*} $$
This implies (by Markov’s inequality) that
![]() $\sum _{x < n \leq x+y} f(n)$
converges in probability to 0 rather than converging to a standard Gaussian, when renormalised by its standard deviation. As Soundararajan and Xu [Reference Soundararajan and Xu22] remark, by looking inside the proofs from [Reference Harper10], one can show that
$\sum _{x < n \leq x+y} f(n)$
converges in probability to 0 rather than converging to a standard Gaussian, when renormalised by its standard deviation. As Soundararajan and Xu [Reference Soundararajan and Xu22] remark, by looking inside the proofs from [Reference Harper10], one can show that
![]() $\mathbb {E} \frac {|\sum _{x < n \leq x+y} f(n)|}{\sqrt {y}} \rightarrow 0$
even for somewhat smaller y. Thus, there is at least one qualitative transition in the distributional behaviour of
$\mathbb {E} \frac {|\sum _{x < n \leq x+y} f(n)|}{\sqrt {y}} \rightarrow 0$
even for somewhat smaller y. Thus, there is at least one qualitative transition in the distributional behaviour of
![]() $\sum _{x < n \leq x+y} f(n)$
when y approaches x, and the exact location and nature of this remains to be understood.
$\sum _{x < n \leq x+y} f(n)$
when y approaches x, and the exact location and nature of this remains to be understood.
As also noted earlier, the author believes that
![]() $\sum _{x < n \leq x+y} f(n)$
will be a good model for the behaviour of
$\sum _{x < n \leq x+y} f(n)$
will be a good model for the behaviour of
![]() $\sum _{x < n \leq x+y} \chi (n)$
where
$\sum _{x < n \leq x+y} \chi (n)$
where
![]() $x, y(x)$
are fixed and the character
$x, y(x)$
are fixed and the character
![]() $\chi $
varies mod q, at least provided
$\chi $
varies mod q, at least provided
![]() $x \leq \sqrt {q}$
, say (for x close to q, one will again need to be more careful to account for the periodicity of
$x \leq \sqrt {q}$
, say (for x close to q, one will again need to be more careful to account for the periodicity of
![]() $\chi $
). It would be very interesting to obtain rigorous results on the distribution of
$\chi $
). It would be very interesting to obtain rigorous results on the distribution of
![]() $\sum _{x < n \leq x+y} \chi (n)$
for varying
$\sum _{x < n \leq x+y} \chi (n)$
for varying
![]() $\chi $
.
$\chi $
.
Finally, we might wonder the following.
-
(iv) When
 $f(n)$
is a realisation of a Steinhaus or (extended) Rademacher random multiplicative function, what is the distribution of
$f(n)$
is a realisation of a Steinhaus or (extended) Rademacher random multiplicative function, what is the distribution of
 $\sum _{x < n \leq x+H} f(n)$
as x varies over a long interval?
$\sum _{x < n \leq x+H} f(n)$
as x varies over a long interval?
Although the proofs of Theorems 3 and 4 use the random multiplicative model
![]() $f(n)$
for
$f(n)$
for
![]() $\chi (n)$
, they do not address (iv) because they only use this after first passing to the representation (1.2), the truth of which depends on special properties of Dirichlet characters. Our arguments say nothing directly about the ‘model’ object
$\chi (n)$
, they do not address (iv) because they only use this after first passing to the representation (1.2), the truth of which depends on special properties of Dirichlet characters. Our arguments say nothing directly about the ‘model’ object
![]() $\sum _{x < n \leq x+H} f(n)$
. Of course, a little care is required to sensibly interpret question (iv). For example, the function
$\sum _{x < n \leq x+H} f(n)$
. Of course, a little care is required to sensibly interpret question (iv). For example, the function
![]() $f(n)$
that is 1 for all n on some long initial segment is a realisation of a random multiplicative function and has rather exceptional behaviour, but it is a realisation that occurs with extremely small probability. A natural problem might be to investigate the distribution of
$f(n)$
that is 1 for all n on some long initial segment is a realisation of a random multiplicative function and has rather exceptional behaviour, but it is a realisation that occurs with extremely small probability. A natural problem might be to investigate the distribution of
![]() $\sum _{x < n \leq x+H} f(n)$
for ‘most’ realisations of f, somewhat analogously to Theorems 3 and 4. Relevant work in the literature includes Najnudel’s paper [Reference Najnudel18], which explores the joint distribution of the tuple
$\sum _{x < n \leq x+H} f(n)$
for ‘most’ realisations of f, somewhat analogously to Theorems 3 and 4. Relevant work in the literature includes Najnudel’s paper [Reference Najnudel18], which explores the joint distribution of the tuple
![]() $(f(x),f(x+1), \ldots , f(x+H))$
for x varying and H fixed (or slowly growing).
$(f(x),f(x+1), \ldots , f(x+H))$
for x varying and H fixed (or slowly growing).
Remark added in review, March 2024. Following the release of a preprint version of the present article, question (iv) was investigated by Pandey, Wang and Xu [Reference Pandey, Wang and Xu19]. Using a moment method, they can show that
![]() $\frac {1}{\sqrt {H}} \sum _{x < n \leq x+H} f(n)$
typically (i.e., for most realisations of Steinhaus random multiplicative
$\frac {1}{\sqrt {H}} \sum _{x < n \leq x+H} f(n)$
typically (i.e., for most realisations of Steinhaus random multiplicative
![]() $f(n)$
) has an approximately Gaussian distribution as
$f(n)$
) has an approximately Gaussian distribution as
![]() $x \leq X$
varies, provided that
$x \leq X$
varies, provided that
![]() $H = H(X) \rightarrow \infty $
but
$H = H(X) \rightarrow \infty $
but
![]() $\log (X/H)/\log \log X \rightarrow \infty $
as
$\log (X/H)/\log \log X \rightarrow \infty $
as
![]() $X \rightarrow \infty $
.
$X \rightarrow \infty $
.
2 Tools for Theorems 1 and 2
The proofs of Theorems 1 and 2 rest on the following simple principle.
Probability Result 1. Let
![]() $0 \leq \tau < 1$
, and suppose
$0 \leq \tau < 1$
, and suppose
![]() $(V_n)_{n=1}^{\infty }$
is a sequence of real or complex valued random variables satisfying
$(V_n)_{n=1}^{\infty }$
is a sequence of real or complex valued random variables satisfying
![]() $\mathbb {E}|V_n|^2 \leq \tau $
for all n. Then if Z is any real or complex valued random variable such that
$\mathbb {E}|V_n|^2 \leq \tau $
for all n. Then if Z is any real or complex valued random variable such that
![]() $\mathbb {E}|Z|^2 = 1$
, we have
$\mathbb {E}|Z|^2 = 1$
, we have
Proof of Probability Result 1.
Choose
![]() $a \in \mathbb {R}$
such that
$a \in \mathbb {R}$
such that
![]() $\mathbb {E}\min \{|Z|^2, a^2\} \geq (1+\tau )/2$
(such a exists by the monotone convergence theorem). Since
$\mathbb {E}\min \{|Z|^2, a^2\} \geq (1+\tau )/2$
(such a exists by the monotone convergence theorem). Since
![]() $v \mapsto \min \{|v|^2 , a^2\}$
is a continuous bounded function on
$v \mapsto \min \{|v|^2 , a^2\}$
is a continuous bounded function on
![]() $\mathbb {C}$
, if we had
$\mathbb {C}$
, if we had
![]() $V_n \stackrel {d}{\rightarrow } Z$
, then we would have
$V_n \stackrel {d}{\rightarrow } Z$
, then we would have
But this is impossible since clearly
![]() $\mathbb {E} \min \{|V_n|^2 , a^2\} \leq \mathbb {E}|V_n|^2 \leq \tau < (1+\tau )/2$
.
$\mathbb {E} \min \{|V_n|^2 , a^2\} \leq \mathbb {E}|V_n|^2 \leq \tau < (1+\tau )/2$
.
We remark that although Probability Result 1 is simple, there is a non-trivial issue involved which it is important to recognise. Thus, the analogous statement in which for some
![]() $\nu> 1$
our sequence satisfied
$\nu> 1$
our sequence satisfied
![]() $\mathbb {E} |V_n|^2 \geq \nu $
for all n would be false, as can easily be shown by examples. In general, the failure of moments to converge to the moments of a supposed limit distribution need not, by itself, imply that convergence in distribution is not happening since moments may be inflated by events whose probabilities tend to zero, and which are therefore irrelevant to convergence in distribution.
$\mathbb {E} |V_n|^2 \geq \nu $
for all n would be false, as can easily be shown by examples. In general, the failure of moments to converge to the moments of a supposed limit distribution need not, by itself, imply that convergence in distribution is not happening since moments may be inflated by events whose probabilities tend to zero, and which are therefore irrelevant to convergence in distribution.
As explained in the Introduction, Theorems 1 and 2 will also rely on the existence of non-principal characters with large partial sums. In the non-real case, the existence of such characters follows immediately from work of Granville and Soundararajan [Reference Granville and Soundararajan6].
Number Theory Result 1 (see Theorem 3 of Granville and Soundararajan [Reference Granville and Soundararajan6], 2001).
Let
![]() $A> 0$
, and suppose q is a prime (say) that is sufficiently large in terms of A. Then for any
$A> 0$
, and suppose q is a prime (say) that is sufficiently large in terms of A. Then for any
![]() $2 \leq x \leq \log ^{A}q$
, there exist at least
$2 \leq x \leq \log ^{A}q$
, there exist at least
![]() $q^{1 - \frac {2}{\log x}}$
characters
$q^{1 - \frac {2}{\log x}}$
characters
![]() $\chi $
mod q for which
$\chi $
mod q for which
 $$ \begin{align*}\left| \sum_{n \leq x} \chi(n) \right| \geq x \rho(A) \left(1 + O \left(\frac{1}{\log x} + \frac{\log x (\log\log\log q)^2}{(\log\log q)^2}\right) \right) ,\end{align*} $$
$$ \begin{align*}\left| \sum_{n \leq x} \chi(n) \right| \geq x \rho(A) \left(1 + O \left(\frac{1}{\log x} + \frac{\log x (\log\log\log q)^2}{(\log\log q)^2}\right) \right) ,\end{align*} $$
where
![]() $\rho (A)> 0$
denotes the Dickman function.
$\rho (A)> 0$
denotes the Dickman function.
In the real case, Granville and Soundararajan (see Theorem 9 of [Reference Granville and Soundararajan6]) also proved that for any fixed A, if q is large and
![]() $x = ((1/3)\log q)^A$
, then there exists a fundamental discriminant
$x = ((1/3)\log q)^A$
, then there exists a fundamental discriminant
![]() $q \leq |D| \leq 2q$
for which
$q \leq |D| \leq 2q$
for which
 $$ \begin{align*}\sum_{n \leq x} \left(\frac{D}{n}\right) \geq x (\rho(A) + o(1)) .\end{align*} $$
$$ \begin{align*}\sum_{n \leq x} \left(\frac{D}{n}\right) \geq x (\rho(A) + o(1)) .\end{align*} $$
Unfortunately this is not quite sufficient for our purposes because we need to find biased real characters
![]() $\left (\frac {\cdot }{q}\right )$
where q is prime. But by reorganising Granville and Soundararajan’s proof a little, and inserting information about the zero-free region and exceptional zeros of Dirichlet L-functions, one can prove such a statement. This has been done by Kalmynin [Reference Kalmynin13].
$\left (\frac {\cdot }{q}\right )$
where q is prime. But by reorganising Granville and Soundararajan’s proof a little, and inserting information about the zero-free region and exceptional zeros of Dirichlet L-functions, one can prove such a statement. This has been done by Kalmynin [Reference Kalmynin13].
Number Theory Result 2 (see Theorem 3 of Kalmynin [Reference Kalmynin13], 2019).
For any fixed
![]() $B> 0$
, there exists a small constant
$B> 0$
, there exists a small constant
![]() $c(B)> 0$
such that the following is true. If Q is sufficiently large in terms of B, then for any
$c(B)> 0$
such that the following is true. If Q is sufficiently large in terms of B, then for any
![]() $1 \leq x \leq \log ^{B}Q$
, there exists a prime
$1 \leq x \leq \log ^{B}Q$
, there exists a prime
![]() $Q < q \leq 2Q$
such that
$Q < q \leq 2Q$
such that
 $$ \begin{align*}\sum_{n \leq x} \left(\frac{n}{q}\right) \geq c(B) x .\end{align*} $$
$$ \begin{align*}\sum_{n \leq x} \left(\frac{n}{q}\right) \geq c(B) x .\end{align*} $$
Proof of Number Theory Result 2.
Theorem 3 of Kalmynin [Reference Kalmynin13] directly implies Number Theory Result 2 provided that
![]() $B \geq 1$
and
$B \geq 1$
and
![]() $x = \log ^{B}Q$
. However, the lower bound for
$x = \log ^{B}Q$
. However, the lower bound for
![]() $S_{0}(Q)$
obtained in Kalmynin’s proof implies that one can find primes
$S_{0}(Q)$
obtained in Kalmynin’s proof implies that one can find primes
![]() $Q < q \leq 2Q$
such that
$Q < q \leq 2Q$
such that
![]() $\left (\frac {n}{q}\right ) = 1$
for all
$\left (\frac {n}{q}\right ) = 1$
for all
![]() $n \leq \log ^{1/3}Q$
. This means that if
$n \leq \log ^{1/3}Q$
. This means that if
![]() $x \leq \log ^{1/3}Q$
, then one can make
$x \leq \log ^{1/3}Q$
, then one can make
![]() $\sum _{n \leq x} \left (\frac {n}{q}\right )$
maximally large. And if
$\sum _{n \leq x} \left (\frac {n}{q}\right )$
maximally large. And if
![]() $\log ^{1/3}Q < x \leq \log ^{B}Q$
, then one can run Kalmynin’s proof with the sum over
$\log ^{1/3}Q < x \leq \log ^{B}Q$
, then one can run Kalmynin’s proof with the sum over
![]() $n \leq \log ^{B}Q$
replaced by a sum over
$n \leq \log ^{B}Q$
replaced by a sum over
![]() $n \leq x$
without changing anything, giving the desired conclusion.
$n \leq x$
without changing anything, giving the desired conclusion.
3 Proof of Theorem 1
Let
![]() $K \geq 1$
. If
$K \geq 1$
. If
![]() $\chi $
is a primitive character modulo q, then Pólya’s Fourier expansion (see, for example, display (9.19) of Montgomery and Vaughan [Reference Montgomery and Vaughan17], noting that the restriction
$\chi $
is a primitive character modulo q, then Pólya’s Fourier expansion (see, for example, display (9.19) of Montgomery and Vaughan [Reference Montgomery and Vaughan17], noting that the restriction
![]() $K \leq q^{1-\epsilon }$
there is unnecessary if one is happy with a general error term
$K \leq q^{1-\epsilon }$
there is unnecessary if one is happy with a general error term
![]() $\frac {q\log q}{K}$
rather than
$\frac {q\log q}{K}$
rather than
![]() $\frac {\phi (q) \log q}{K}$
) yields that
$\frac {\phi (q) \log q}{K}$
) yields that
 $$ \begin{align*}\sum_{n \leq x} \chi(n) = \frac{\tau(\chi)}{2\pi i} \sum_{0 < |k| \leq K} \frac{\overline{\chi}(-k)}{k} (e(kx/q) - 1) + O \left(1 + \frac{q\log q}{K}\right) ,\end{align*} $$
$$ \begin{align*}\sum_{n \leq x} \chi(n) = \frac{\tau(\chi)}{2\pi i} \sum_{0 < |k| \leq K} \frac{\overline{\chi}(-k)}{k} (e(kx/q) - 1) + O \left(1 + \frac{q\log q}{K}\right) ,\end{align*} $$
so in particular,
 $$ \begin{align} S_{\chi, H}(x) = \frac{\tau(\chi)}{2\pi i} \sum_{0 < |k| < q/2} \frac{\overline{\chi}(-k)}{k} e(kx/q) (e(kH/q) - 1) + O(\log q). \end{align} $$
$$ \begin{align} S_{\chi, H}(x) = \frac{\tau(\chi)}{2\pi i} \sum_{0 < |k| < q/2} \frac{\overline{\chi}(-k)}{k} e(kx/q) (e(kH/q) - 1) + O(\log q). \end{align} $$
Here,
![]() $\tau (\chi )$
denotes the Gauss sum, having absolute value
$\tau (\chi )$
denotes the Gauss sum, having absolute value
![]() $\sqrt {q}$
for primitive
$\sqrt {q}$
for primitive
![]() $\chi $
.
$\chi $
.
Recall that X denotes a random variable having the discrete uniform distribution on
![]() $\{0,1,\ldots ,q-1\}$
(this is the randomness with respect to which we will shortly calculate expectations
$\{0,1,\ldots ,q-1\}$
(this is the randomness with respect to which we will shortly calculate expectations
![]() $\mathbb {E}$
), and that
$\mathbb {E}$
), and that
![]() $H = H(q) = q/\log ^{A}q$
, and that
$H = H(q) = q/\log ^{A}q$
, and that
![]() $\chi = \left (\frac {\cdot }{q}\right )$
is real-valued in Theorem 1. Next let
$\chi = \left (\frac {\cdot }{q}\right )$
is real-valued in Theorem 1. Next let
![]() $0 < \delta \leq 1$
be a parameter, that will be fixed later, and define
$0 < \delta \leq 1$
be a parameter, that will be fixed later, and define
![]() $\alpha = \alpha (\delta ) \in \mathbb {R}$
by
$\alpha = \alpha (\delta ) \in \mathbb {R}$
by
 $$ \begin{align*}\sum_{1 \leq k \leq \delta q/H} \overline{\chi}(-k) = \sum_{1 \leq k \leq \delta q/H} \chi(-k) = \alpha \sum_{1 \leq k \leq \delta q/H} 1 ,\end{align*} $$
$$ \begin{align*}\sum_{1 \leq k \leq \delta q/H} \overline{\chi}(-k) = \sum_{1 \leq k \leq \delta q/H} \chi(-k) = \alpha \sum_{1 \leq k \leq \delta q/H} 1 ,\end{align*} $$
and define
 $$ \begin{align*}G_{\chi, H}(x) := \frac{\alpha \tau(\chi) H}{q} \sum_{1 \leq k \leq \delta q/H} e(kx/q) .\end{align*} $$
$$ \begin{align*}G_{\chi, H}(x) := \frac{\alpha \tau(\chi) H}{q} \sum_{1 \leq k \leq \delta q/H} e(kx/q) .\end{align*} $$
As discussed in the Introduction,
![]() $G_{\chi , H}(x)$
is the scaled Dirichlet kernel that we shall strategically subtract from
$G_{\chi , H}(x)$
is the scaled Dirichlet kernel that we shall strategically subtract from
![]() $S_{\chi , H}(x)$
. (The small parameter
$S_{\chi , H}(x)$
. (The small parameter
![]() $\delta $
is only present for technical reasons, to control lower order terms in Taylor expansions of the complex exponential.)
$\delta $
is only present for technical reasons, to control lower order terms in Taylor expansions of the complex exponential.)
Before embarking on our main computations, we record some basic observations. By expanding the square and using the fact that
![]() $\mathbb {E} e(k_1 X/q) e(-k_2 X/q) = \mathbb {E} e((k_1 - k_2)X/q) = 0$
when
$\mathbb {E} e(k_1 X/q) e(-k_2 X/q) = \mathbb {E} e((k_1 - k_2)X/q) = 0$
when
![]() $-q/2 < k_1 \neq k_2 < q/2$
, we find
$-q/2 < k_1 \neq k_2 < q/2$
, we find
 $$ \begin{align*}\mathbb{E}|G_{\chi, H}(X)|^2 = \frac{\alpha^2 H^2}{q} \mathbb{E}|\sum_{1 \leq k \leq \delta q/H} e(kX/q)|^2 = \frac{\alpha^2 H^2}{q} \sum_{1 \leq k \leq \delta q/H} 1 \leq H ,\end{align*} $$
$$ \begin{align*}\mathbb{E}|G_{\chi, H}(X)|^2 = \frac{\alpha^2 H^2}{q} \mathbb{E}|\sum_{1 \leq k \leq \delta q/H} e(kX/q)|^2 = \frac{\alpha^2 H^2}{q} \sum_{1 \leq k \leq \delta q/H} 1 \leq H ,\end{align*} $$
as well as
 $$ \begin{align*}\mathbb{E}\Bigg|\frac{\tau(\chi)}{2\pi i} \sum_{0 < |k| < q/2} \frac{\overline{\chi}(-k)}{k} e(kX/q) (e(kH/q) - 1) \Bigg|^2 = \frac{q}{(2\pi)^2} \sum_{0 < |k| < q/2} \frac{1}{k^2} |e(kH/q) - 1|^2 .\end{align*} $$
$$ \begin{align*}\mathbb{E}\Bigg|\frac{\tau(\chi)}{2\pi i} \sum_{0 < |k| < q/2} \frac{\overline{\chi}(-k)}{k} e(kX/q) (e(kH/q) - 1) \Bigg|^2 = \frac{q}{(2\pi)^2} \sum_{0 < |k| < q/2} \frac{1}{k^2} |e(kH/q) - 1|^2 .\end{align*} $$
Since
![]() $\mathbb {E}|S_{\chi , H}(X)|^2 = \mathbb {E}|\sum _{X < n \leq X+H} \chi (n)|^2$
is
$\mathbb {E}|S_{\chi , H}(X)|^2 = \mathbb {E}|\sum _{X < n \leq X+H} \chi (n)|^2$
is
(explaining why
![]() $\frac {S_{\chi , H}(X)}{\sqrt {H}}$
is the natural renormalisation to consider), we deduce that
$\frac {S_{\chi , H}(X)}{\sqrt {H}}$
is the natural renormalisation to consider), we deduce that
 $$ \begin{align*} \frac{q}{(2\pi)^2} \sum_{0 < |k| < q/2} \frac{1}{k^2} |e(kH/q) - 1|^2 & = \mathbb{E}|S_{\chi, H}(X) + O(\log q)|^2 \nonumber \\ & = \mathbb{E}|S_{\chi, H}(X)|^2 + O(\log q \mathbb{E}|S_{\chi, H}(X)| + \log^{2}q) \nonumber \\ & = (1+o(1))H \nonumber \end{align*} $$
$$ \begin{align*} \frac{q}{(2\pi)^2} \sum_{0 < |k| < q/2} \frac{1}{k^2} |e(kH/q) - 1|^2 & = \mathbb{E}|S_{\chi, H}(X) + O(\log q)|^2 \nonumber \\ & = \mathbb{E}|S_{\chi, H}(X)|^2 + O(\log q \mathbb{E}|S_{\chi, H}(X)| + \log^{2}q) \nonumber \\ & = (1+o(1))H \nonumber \end{align*} $$
when
![]() $H = H(q) = q/\log ^{A}q$
(and indeed on a much larger range of H as well).
$H = H(q) = q/\log ^{A}q$
(and indeed on a much larger range of H as well).
Next, using (3.1), expanding the square, and calculating as above (and using the Cauchy–Schwarz inequality and the above estimates of
![]() $\mathbb {E}|G_{\chi , H}(X)|^2$
and
$\mathbb {E}|G_{\chi , H}(X)|^2$
and
![]() $\mathbb {E}|S_{\chi , H}(X)|^2$
to control the contribution from the
$\mathbb {E}|S_{\chi , H}(X)|^2$
to control the contribution from the
![]() $O(\log q)$
term), we find
$O(\log q)$
term), we find
 $$ \begin{align} & \mathbb{E}|S_{\chi, H}(X) - G_{\chi, H}(X)|^2 \nonumber \\ &\quad = \mathbb{E}\Bigg|\tau(\chi) \sum_{1 \leq k \leq \delta q/H} e(kX/q) \left(\frac{\overline{\chi}(-k)}{k} \frac{(e(kH/q) - 1)}{2\pi i} - \frac{\alpha H}{q} \right) + \nonumber \\ &\qquad + \frac{\tau(\chi)}{2\pi i} \sum_{\substack{0 < |k| < q/2 , \\ k \notin [1,\delta q/H]}} \frac{\overline{\chi}(-k)}{k} e(kX/q) (e(kH/q) - 1) + O(\log q) \Bigg|^2 \nonumber \\ &\quad = q \sum_{1 \leq k \leq \delta q/H} \left|\frac{\overline{\chi}(-k)}{k} \frac{(e(kH/q) - 1)}{2\pi i} - \frac{\alpha H}{q} \right|^2 + \frac{q}{(2\pi)^2} \sum_{\substack{0 < |k| < q/2 , \\ k \notin [1,\delta q/H]}} \frac{1}{k^2} |e(kH/q) - 1|^2 + \nonumber \\ &\qquad + O(\sqrt{H} \log q + \log^{2}q ). \end{align} $$
$$ \begin{align} & \mathbb{E}|S_{\chi, H}(X) - G_{\chi, H}(X)|^2 \nonumber \\ &\quad = \mathbb{E}\Bigg|\tau(\chi) \sum_{1 \leq k \leq \delta q/H} e(kX/q) \left(\frac{\overline{\chi}(-k)}{k} \frac{(e(kH/q) - 1)}{2\pi i} - \frac{\alpha H}{q} \right) + \nonumber \\ &\qquad + \frac{\tau(\chi)}{2\pi i} \sum_{\substack{0 < |k| < q/2 , \\ k \notin [1,\delta q/H]}} \frac{\overline{\chi}(-k)}{k} e(kX/q) (e(kH/q) - 1) + O(\log q) \Bigg|^2 \nonumber \\ &\quad = q \sum_{1 \leq k \leq \delta q/H} \left|\frac{\overline{\chi}(-k)}{k} \frac{(e(kH/q) - 1)}{2\pi i} - \frac{\alpha H}{q} \right|^2 + \frac{q}{(2\pi)^2} \sum_{\substack{0 < |k| < q/2 , \\ k \notin [1,\delta q/H]}} \frac{1}{k^2} |e(kH/q) - 1|^2 + \nonumber \\ &\qquad + O(\sqrt{H} \log q + \log^{2}q ). \end{align} $$
Using the Taylor expansion
![]() $e(kH/q) = 1 + 2\pi i kH/q + O((kH/q)^2)$
, the first sum here is seen to be
$e(kH/q) = 1 + 2\pi i kH/q + O((kH/q)^2)$
, the first sum here is seen to be
 $$ \begin{align*} q \sum_{1 \leq k \leq \delta q/H} \left|\frac{\overline{\chi}(-k)H}{q} + O\left(\frac{\delta H}{q}\right) - \frac{\alpha H}{q} \right|^2 & = \frac{H^2}{q} \sum_{1 \leq k \leq \delta q/H} \left|\overline{\chi}(-k) + O(\delta) - \alpha \right|^2 \nonumber \\ & = \frac{H^2}{q} \sum_{1 \leq k \leq \delta q/H} \left|\overline{\chi}(-k) - \alpha \right|^2 + O(\delta^2 H). \nonumber \end{align*} $$
$$ \begin{align*} q \sum_{1 \leq k \leq \delta q/H} \left|\frac{\overline{\chi}(-k)H}{q} + O\left(\frac{\delta H}{q}\right) - \frac{\alpha H}{q} \right|^2 & = \frac{H^2}{q} \sum_{1 \leq k \leq \delta q/H} \left|\overline{\chi}(-k) + O(\delta) - \alpha \right|^2 \nonumber \\ & = \frac{H^2}{q} \sum_{1 \leq k \leq \delta q/H} \left|\overline{\chi}(-k) - \alpha \right|^2 + O(\delta^2 H). \nonumber \end{align*} $$
Moreover, since we chose
![]() $\alpha $
to be the mean value of
$\alpha $
to be the mean value of
![]() $\overline {\chi }(-k) (= \chi (-k))$
over the interval
$\overline {\chi }(-k) (= \chi (-k))$
over the interval
![]() $1 \leq k \leq \delta q/H$
, this simplifies to
$1 \leq k \leq \delta q/H$
, this simplifies to
 $$ \begin{align*}(1- \alpha^2) \frac{H^2}{q} \Bigg( \sum_{1 \leq k \leq \delta q/H} 1 \Bigg) + O(\delta^2 H) ,\end{align*} $$
$$ \begin{align*}(1- \alpha^2) \frac{H^2}{q} \Bigg( \sum_{1 \leq k \leq \delta q/H} 1 \Bigg) + O(\delta^2 H) ,\end{align*} $$
which we can rewrite (again using the Taylor expansion of the exponential) as
 $$ \begin{align*} & \frac{H^2}{q} \Bigg( \sum_{1 \leq k \leq \delta q/H} 1 \Bigg) - \delta \alpha^2 H + O \left(\delta^2 H + \frac{H^2}{q}\right) \\ &\quad = \frac{q}{(2\pi)^2} \sum_{1 \leq k \leq \delta q/H} \frac{1}{k^2} |e(kH/q) - 1|^2 - \delta \alpha^2 H + O \left(\delta^2 H + \frac{H^2}{q}\right) .\end{align*} $$
$$ \begin{align*} & \frac{H^2}{q} \Bigg( \sum_{1 \leq k \leq \delta q/H} 1 \Bigg) - \delta \alpha^2 H + O \left(\delta^2 H + \frac{H^2}{q}\right) \\ &\quad = \frac{q}{(2\pi)^2} \sum_{1 \leq k \leq \delta q/H} \frac{1}{k^2} |e(kH/q) - 1|^2 - \delta \alpha^2 H + O \left(\delta^2 H + \frac{H^2}{q}\right) .\end{align*} $$
Inserting this in (3.2), and using our earlier calculation that
![]() $\frac {q}{(2\pi )^2} \sum _{0 < |k| < q/2} \frac {1}{k^2} |e(kH/q) - 1|^2 = (1+o(1))H$
, we deduce
$\frac {q}{(2\pi )^2} \sum _{0 < |k| < q/2} \frac {1}{k^2} |e(kH/q) - 1|^2 = (1+o(1))H$
, we deduce
In particular, note that if
![]() $H(q) = q/\log ^{A}q$
, then we have
$H(q) = q/\log ^{A}q$
, then we have
![]() $\delta q/H \leq q/H = \log ^{A}q$
. Thus, by Number Theory Result 2, there exist arbitrarily large primes q for which, with
$\delta q/H \leq q/H = \log ^{A}q$
. Thus, by Number Theory Result 2, there exist arbitrarily large primes q for which, with
![]() $\chi = \left (\frac {\cdot }{q}\right )$
, we have
$\chi = \left (\frac {\cdot }{q}\right )$
, we have
 $$ \begin{align*}\Bigg| \sum_{1 \leq k \leq \delta q/H} \overline{\chi}(-k) \Bigg| = \Bigg| \sum_{1 \leq k \leq \delta q/H} \chi(k) \Bigg| \geq c(A) \delta q/H .\end{align*} $$
$$ \begin{align*}\Bigg| \sum_{1 \leq k \leq \delta q/H} \overline{\chi}(-k) \Bigg| = \Bigg| \sum_{1 \leq k \leq \delta q/H} \chi(k) \Bigg| \geq c(A) \delta q/H .\end{align*} $$
In other words, for such q, we will have
![]() $|\alpha | \geq c(A)$
. So if we fix the choice
$|\alpha | \geq c(A)$
. So if we fix the choice
![]() $\delta = c_0 c(A)^2$
, for a suitably small absolute constant
$\delta = c_0 c(A)^2$
, for a suitably small absolute constant
![]() $c_0> 0$
to neutralise the implicit constant in the
$c_0> 0$
to neutralise the implicit constant in the
![]() $O(\delta ^2)$
term, we will have
$O(\delta ^2)$
term, we will have
 $$ \begin{align} \mathbb{E}\left| \frac{S_{\chi, H}(X) - G_{\chi, H}(X)}{\sqrt{H}} \right|^2 = 1 - \delta\alpha^2 + O(\delta^2) + o(1) \leq 1 - (c_{0}/2) c(A)^4 \end{align} $$
$$ \begin{align} \mathbb{E}\left| \frac{S_{\chi, H}(X) - G_{\chi, H}(X)}{\sqrt{H}} \right|^2 = 1 - \delta\alpha^2 + O(\delta^2) + o(1) \leq 1 - (c_{0}/2) c(A)^4 \end{align} $$
whenever q is a large enough prime coming from Number Theory Result 2.
Now on the other hand, using the formula for summing a geometric progression, we may calculate explicitly that, with
![]() $|| \cdot ||$
denoting distance to the nearest integer,
$|| \cdot ||$
denoting distance to the nearest integer,
 $$ \begin{align*}\mathbb{E}|G_{\chi, H}(X)| &= \frac{|\alpha| H}{\sqrt{q}} \mathbb{E}\left|\sum_{1 \leq k \leq \delta q/H} e(kX/q) \right| \\ &\ll \frac{H}{\sqrt{q}} \mathbb{E} \min\left\{\frac{\delta q}{H}, \frac{1}{||X/q||} \right\} \ll \frac{H}{\sqrt{q}} (1 + \log(\delta q/H)) ,\end{align*} $$
$$ \begin{align*}\mathbb{E}|G_{\chi, H}(X)| &= \frac{|\alpha| H}{\sqrt{q}} \mathbb{E}\left|\sum_{1 \leq k \leq \delta q/H} e(kX/q) \right| \\ &\ll \frac{H}{\sqrt{q}} \mathbb{E} \min\left\{\frac{\delta q}{H}, \frac{1}{||X/q||} \right\} \ll \frac{H}{\sqrt{q}} (1 + \log(\delta q/H)) ,\end{align*} $$
and therefore,
 $$ \begin{align*}\mathbb{E}\left|\frac{G_{\chi, H}(X)}{\sqrt{H}} \right| \ll \frac{(1 + \log(\delta q/H))}{\sqrt{q/H}} \ll \frac{\log(q/H)}{\sqrt{q/H}} \rightarrow 0 \quad \text{as } q \rightarrow \infty .\end{align*} $$
$$ \begin{align*}\mathbb{E}\left|\frac{G_{\chi, H}(X)}{\sqrt{H}} \right| \ll \frac{(1 + \log(\delta q/H))}{\sqrt{q/H}} \ll \frac{\log(q/H)}{\sqrt{q/H}} \rightarrow 0 \quad \text{as } q \rightarrow \infty .\end{align*} $$
By Markov’s inequality, it follows that
![]() $\frac {G_{\chi , H}(X)}{\sqrt {H}}$
converges in probability to zero as
$\frac {G_{\chi , H}(X)}{\sqrt {H}}$
converges in probability to zero as
![]() $q \rightarrow \infty $
, and so if
$q \rightarrow \infty $
, and so if
![]() $\frac {S_{\chi , H}(X)}{\sqrt {H}} \stackrel {d}{\rightarrow } N(0,1)$
, then we must also have
$\frac {S_{\chi , H}(X)}{\sqrt {H}} \stackrel {d}{\rightarrow } N(0,1)$
, then we must also have
![]() $\frac {S_{\chi , H}(X) - G_{\chi , H}(X)}{\sqrt {H}} \stackrel {d}{\rightarrow } N(0,1)$
.
$\frac {S_{\chi , H}(X) - G_{\chi , H}(X)}{\sqrt {H}} \stackrel {d}{\rightarrow } N(0,1)$
.
But combining Probability Result 1 with (3.3), we see this convergence in distribution is impossible, which proves Theorem 1.
4 Proof of Theorem 2
The proof of Theorem 2 is extremely similar to that of Theorem 1, so we simply make a few remarks to reassure the reader that no additional difficulties arise.
Indeed, this time, we define
![]() $\alpha = \alpha (\delta ) \in \mathbb {C}$
by
$\alpha = \alpha (\delta ) \in \mathbb {C}$
by
 $$ \begin{align*}\sum_{1 \leq k \leq \delta q/H} \overline{\chi}(-k) = \alpha \sum_{1 \leq k \leq \delta q/H} 1 ,\end{align*} $$
$$ \begin{align*}\sum_{1 \leq k \leq \delta q/H} \overline{\chi}(-k) = \alpha \sum_{1 \leq k \leq \delta q/H} 1 ,\end{align*} $$
and again we set
 $$ \begin{align*}G_{\chi, H}(x) := \frac{\alpha \tau(\chi) H}{q} \sum_{1 \leq k \leq \delta q/H} e(kx/q) .\end{align*} $$
$$ \begin{align*}G_{\chi, H}(x) := \frac{\alpha \tau(\chi) H}{q} \sum_{1 \leq k \leq \delta q/H} e(kx/q) .\end{align*} $$
Then the same calculations as in the proof of Theorem 1 show that
 $$ \begin{align*} & \mathbb{E}|S_{\chi, H}(X) - G_{\chi, H}(X)|^2 \nonumber \\ & = (1- |\alpha|^2) \frac{H^2}{q} \sum_{1 \leq k \leq \delta q/H} 1 + O(\delta^2 H) + \frac{q}{(2\pi)^2} \sum_{\substack{0 < |k| < q/2 , \\ k \notin [1,\delta q/H]}} \frac{1}{k^2} |e(kH/q) - 1|^2 + \nonumber \\ & + O(\sqrt{H} \log q + \log^{2}q ) \nonumber \\ & = (1 - \delta|\alpha|^2 + O(\delta^2) + o(1))H. \nonumber \end{align*} $$
$$ \begin{align*} & \mathbb{E}|S_{\chi, H}(X) - G_{\chi, H}(X)|^2 \nonumber \\ & = (1- |\alpha|^2) \frac{H^2}{q} \sum_{1 \leq k \leq \delta q/H} 1 + O(\delta^2 H) + \frac{q}{(2\pi)^2} \sum_{\substack{0 < |k| < q/2 , \\ k \notin [1,\delta q/H]}} \frac{1}{k^2} |e(kH/q) - 1|^2 + \nonumber \\ & + O(\sqrt{H} \log q + \log^{2}q ) \nonumber \\ & = (1 - \delta|\alpha|^2 + O(\delta^2) + o(1))H. \nonumber \end{align*} $$
Next, in place of Number Theory Result 2, we can invoke Number Theory Result 1, which implies that for any large prime q, we may find a non-real character
![]() $\chi $
mod q (in fact, several of them) for which
$\chi $
mod q (in fact, several of them) for which
 $$ \begin{align*}\left| \sum_{1 \leq k \leq \delta q/H} \overline{\chi}(-k) \right| = \left| \sum_{1 \leq k \leq \delta q/H} \chi(k) \right| \geq (\rho(A) + o_{\delta, A}(1)) \sum_{1 \leq k \leq \delta q/H} 1 .\end{align*} $$
$$ \begin{align*}\left| \sum_{1 \leq k \leq \delta q/H} \overline{\chi}(-k) \right| = \left| \sum_{1 \leq k \leq \delta q/H} \chi(k) \right| \geq (\rho(A) + o_{\delta, A}(1)) \sum_{1 \leq k \leq \delta q/H} 1 .\end{align*} $$
For such a character, we will have
![]() $|\alpha | \geq \rho (A) + o_{\delta , A}(1)$
, so if we fix the choice
$|\alpha | \geq \rho (A) + o_{\delta , A}(1)$
, so if we fix the choice
![]() $\delta = c \rho (A)^2$
, where
$\delta = c \rho (A)^2$
, where
![]() $c> 0$
is a suitably small absolute constant, then in place of (3.3), we will get
$c> 0$
is a suitably small absolute constant, then in place of (3.3), we will get
 $$ \begin{align*}\mathbb{E}\left| \frac{S_{\chi, H}(X) - G_{\chi, H}(X)}{\sqrt{H}} \right|^2 = 1 - \delta|\alpha|^2 + O(\delta^2) + o(1) \leq 1 - (c/2) \rho(A)^4 ,\end{align*} $$
$$ \begin{align*}\mathbb{E}\left| \frac{S_{\chi, H}(X) - G_{\chi, H}(X)}{\sqrt{H}} \right|^2 = 1 - \delta|\alpha|^2 + O(\delta^2) + o(1) \leq 1 - (c/2) \rho(A)^4 ,\end{align*} $$
provided q is large enough.
Combining this bound with Probability Result 1, and the facts that
![]() $\frac {G_{\chi , H}(X)}{\sqrt {H}} \stackrel {p}{\rightarrow } 0$
and that
$\frac {G_{\chi , H}(X)}{\sqrt {H}} \stackrel {p}{\rightarrow } 0$
and that
![]() $\mathbb {E}|Z_1 + iZ_2|^2 = \mathbb {E} Z_1^2 + \mathbb {E} Z_2^2 = 1$
(where
$\mathbb {E}|Z_1 + iZ_2|^2 = \mathbb {E} Z_1^2 + \mathbb {E} Z_2^2 = 1$
(where
![]() $Z_1 , Z_2$
are independent
$Z_1 , Z_2$
are independent
![]() $N(0,1/2)$
random variables), we conclude that indeed
$N(0,1/2)$
random variables), we conclude that indeed
![]() $\frac {S_{\chi ,H}(X)}{\sqrt {H}} \stackrel {d}{\not \rightarrow } Z_1 + iZ_2$
as
$\frac {S_{\chi ,H}(X)}{\sqrt {H}} \stackrel {d}{\not \rightarrow } Z_1 + iZ_2$
as
![]() $q \rightarrow \infty $
.
$q \rightarrow \infty $
.
5 Tools for Theorems 3 and 4
As discussed in the Introduction, much of the work in the proofs of Theorems 3 and 4 will be done by some results on random multiplicative functions.
Probability Result 2 (See Theorem 1.1 of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1]).
Let
![]() $f(n)$
be an extended Rademacher random multiplicative function. Then uniformly for any large N, any coefficients
$f(n)$
be an extended Rademacher random multiplicative function. Then uniformly for any large N, any coefficients
![]() $(a_n)_{n \leq N}$
bounded in absolute value by 1, any
$(a_n)_{n \leq N}$
bounded in absolute value by 1, any
![]() $1 \leq k \leq c(\frac {\log N}{\log \log N})^{1/3}$
and any
$1 \leq k \leq c(\frac {\log N}{\log \log N})^{1/3}$
and any
![]() $0 \leq j \leq k$
, we have
$0 \leq j \leq k$
, we have
 $$ \begin{align*}\mathbb{E}\Bigg| \int_{0}^{1} \!\left(\sum_{n \leq N} a_n f(n) e(n\theta) \right)^j \! \left(\overline{\sum_{n \leq N} a_n f(n) e(n\theta)} \!\right)^k d\theta - k! \!\left(\sum_{n \leq N} |a_n|^2\right)^k\! \textbf{1}_{j=k} \Bigg|^2 \ll \frac{N^{j+k}}{N^{1/15k}} ,\end{align*} $$
$$ \begin{align*}\mathbb{E}\Bigg| \int_{0}^{1} \!\left(\sum_{n \leq N} a_n f(n) e(n\theta) \right)^j \! \left(\overline{\sum_{n \leq N} a_n f(n) e(n\theta)} \!\right)^k d\theta - k! \!\left(\sum_{n \leq N} |a_n|^2\right)^k\! \textbf{1}_{j=k} \Bigg|^2 \ll \frac{N^{j+k}}{N^{1/15k}} ,\end{align*} $$
where
![]() $\textbf {1}$
denotes the indicator function.
$\textbf {1}$
denotes the indicator function.
Under the same conditions, and provided the
![]() $a_n$
are real, we have
$a_n$
are real, we have
 $$ \begin{align*}\mathbb{E}\Bigg| \int_{0}^{1} \left(\sum_{n \leq N} a_n f(n) \cos(2\pi n\theta) \right)^k d\theta - \frac{k!}{(k/2)! 2^{k/2}} \left(\frac{1}{2} \sum_{n \leq N} |a_n|^2\right)^{k/2} \textbf{1}_{k \; \text{even}} \Bigg|^2 \ll \frac{N^{k}}{N^{1/15k}} ,\end{align*} $$
$$ \begin{align*}\mathbb{E}\Bigg| \int_{0}^{1} \left(\sum_{n \leq N} a_n f(n) \cos(2\pi n\theta) \right)^k d\theta - \frac{k!}{(k/2)! 2^{k/2}} \left(\frac{1}{2} \sum_{n \leq N} |a_n|^2\right)^{k/2} \textbf{1}_{k \; \text{even}} \Bigg|^2 \ll \frac{N^{k}}{N^{1/15k}} ,\end{align*} $$
and the same when
![]() $\sum _{n \leq N} a_n f(n) \cos (2\pi n\theta )$
is replaced by
$\sum _{n \leq N} a_n f(n) \cos (2\pi n\theta )$
is replaced by
![]() $\sum _{n \leq N} a_n f(n) \sin (2\pi n\theta )$
.
$\sum _{n \leq N} a_n f(n) \sin (2\pi n\theta )$
.
Proof of Probability Result 2.
When
![]() $a_n = 1$
for all n, the first statement follows immediately from Theorem 1.1 of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1], after adjusting for the rescaling of the sums by
$a_n = 1$
for all n, the first statement follows immediately from Theorem 1.1 of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1], after adjusting for the rescaling of the sums by
![]() $1/\sqrt {N}$
that they perform but we do not, and handling the easy
$1/\sqrt {N}$
that they perform but we do not, and handling the easy
![]() $j=0$
case that they omit. For general
$j=0$
case that they omit. For general
![]() $a_n$
, one can check that the proof of Theorem 1.1 transfers over straightforwardly since the diagonal contribution to the integral (coming when
$a_n$
, one can check that the proof of Theorem 1.1 transfers over straightforwardly since the diagonal contribution to the integral (coming when
![]() $j=k$
, from summands in
$j=k$
, from summands in
![]() $\left (\sum _{n \leq N} a_n f(n) e(n\theta ) \right )^k$
that are a permutation of the summands in
$\left (\sum _{n \leq N} a_n f(n) e(n\theta ) \right )^k$
that are a permutation of the summands in
![]() $\left (\overline {\sum _{n \leq N} a_n f(n) e(n\theta )} \right )^k$
) has the acceptable form
$\left (\overline {\sum _{n \leq N} a_n f(n) e(n\theta )} \right )^k$
) has the acceptable form
 $$ \begin{align*} & k! \sum_{n_1, \ldots, n_k \leq N} |a_{n_1}|^2 ... |a_{n_k}|^2 + O\Bigg( k! \sum_{\substack{n_1, \ldots, n_k \leq N, \\ n_i \; \text{not all distinct}}} |a_{n_1}|^2 \ldots |a_{n_k}|^2 \Bigg) \\ &\quad = k! \left(\sum_{n \leq N} |a_n|^2\right)^k + O(k! k^2 N^{k-1}) ,\end{align*} $$
$$ \begin{align*} & k! \sum_{n_1, \ldots, n_k \leq N} |a_{n_1}|^2 ... |a_{n_k}|^2 + O\Bigg( k! \sum_{\substack{n_1, \ldots, n_k \leq N, \\ n_i \; \text{not all distinct}}} |a_{n_1}|^2 \ldots |a_{n_k}|^2 \Bigg) \\ &\quad = k! \left(\sum_{n \leq N} |a_n|^2\right)^k + O(k! k^2 N^{k-1}) ,\end{align*} $$
and all off-diagonal contributions continue to satisfy the point-counting bounds of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1] (since the weights
![]() $a_n$
are bounded in absolute value by 1).
$a_n$
are bounded in absolute value by 1).
To deduce the second statement, by writing
![]() $\cos (2\pi n\theta ) = \frac {e(n\theta ) + e(-n\theta )}{2}$
and expanding the k-th power, we can rewrite
$\cos (2\pi n\theta ) = \frac {e(n\theta ) + e(-n\theta )}{2}$
and expanding the k-th power, we can rewrite
![]() $\int _{0}^{1} \left (\sum _{n \leq N} a_n f(n) \cos (2\pi n\theta ) \right )^k d\theta $
as a weighted sum of
$\int _{0}^{1} \left (\sum _{n \leq N} a_n f(n) \cos (2\pi n\theta ) \right )^k d\theta $
as a weighted sum of
![]() $k+1$
terms of the form
$k+1$
terms of the form
 $$ \begin{align*}\int_{0}^{1} \left(\sum_{n \leq N} a_n f(n) e(n\theta) \right)^j \left(\overline{\sum_{n \leq N} a_n f(n) e(n\theta)} \right)^{k-j} d\theta .\end{align*} $$
$$ \begin{align*}\int_{0}^{1} \left(\sum_{n \leq N} a_n f(n) e(n\theta) \right)^j \left(\overline{\sum_{n \leq N} a_n f(n) e(n\theta)} \right)^{k-j} d\theta .\end{align*} $$
Here, we use the fact that
![]() $a_n$
and
$a_n$
and
![]() $f(n)$
are real valued, and so
$f(n)$
are real valued, and so
![]() $\sum _{n \leq N} a_n f(n) e(-n\theta ) = \overline {\sum _{n \leq N} a_n f(n) e(n\theta )}$
. If k is even, then the term with
$\sum _{n \leq N} a_n f(n) e(-n\theta ) = \overline {\sum _{n \leq N} a_n f(n) e(n\theta )}$
. If k is even, then the term with
![]() $j = k/2$
is
$j = k/2$
is
 $$ \begin{align*}\frac{1}{2^k} {{k}\choose{k/2}} \int_{0}^{1} \left(\sum_{n \leq N} a_n f(n) e(n\theta) \right)^{k/2} \left(\overline{\sum_{n \leq N} a_n f(n) e(n\theta)} \right)^{k/2} d\theta ,\end{align*} $$
$$ \begin{align*}\frac{1}{2^k} {{k}\choose{k/2}} \int_{0}^{1} \left(\sum_{n \leq N} a_n f(n) e(n\theta) \right)^{k/2} \left(\overline{\sum_{n \leq N} a_n f(n) e(n\theta)} \right)^{k/2} d\theta ,\end{align*} $$
and from the first part of Probability Result 2, we obtain a corresponding ‘main term’
 $$ \begin{align*}\frac{1}{2^k} {{k}\choose{k/2}} (k/2)! \left(\sum_{n \leq N} |a_n|^2\right)^{k/2} = \frac{k!}{(k/2)! 2^{k/2}} \left(\frac{1}{2} \sum_{n \leq N} |a_n|^2\right)^{k/2} ,\end{align*} $$
$$ \begin{align*}\frac{1}{2^k} {{k}\choose{k/2}} (k/2)! \left(\sum_{n \leq N} |a_n|^2\right)^{k/2} = \frac{k!}{(k/2)! 2^{k/2}} \left(\frac{1}{2} \sum_{n \leq N} |a_n|^2\right)^{k/2} ,\end{align*} $$
as desired. No other values of j produce any main terms. So using the first part of Probability Result 2, along with Minkowski’s inequality, we obtain
 $$ \begin{align*} & \sqrt{ \mathbb{E}\Bigg| \int_{0}^{1} \left(\sum_{n \leq N} a_n f(n) \cos(2\pi n\theta) \right)^k d\theta - \frac{k!}{(k/2)! 2^{k/2}} \left(\frac{1}{2} \sum_{n \leq N} |a_n|^2\right)^{k/2} \textbf{1}_{k \; \text{even}} \Bigg|^2 } \nonumber \\ & \leq \sum_{j=0}^{k} \frac{1}{2^k} {{k}\choose{j}} \nonumber \\ & \times \sqrt{ \mathbb{E}\Bigg| \int_{0}^{1} \left(\sum_{n \leq N} a_n f(n) e(n\theta) \right)^j \left(\overline{\sum_{n \leq N} a_n f(n) e(n\theta)} \right)^{k-j} - j! \left(\sum_{n \leq N} |a_n|^2 \right)^j \textbf{1}_{j=k-j} \Bigg|^2 } \nonumber \\ & \ll \sum_{j=0}^{k} \frac{1}{2^k} {{k}\choose{j}} \sqrt{ \frac{N^{k}}{N^{1/15k}} } = \sqrt{ \frac{N^{k}}{N^{1/15k}} }. \nonumber \end{align*} $$
$$ \begin{align*} & \sqrt{ \mathbb{E}\Bigg| \int_{0}^{1} \left(\sum_{n \leq N} a_n f(n) \cos(2\pi n\theta) \right)^k d\theta - \frac{k!}{(k/2)! 2^{k/2}} \left(\frac{1}{2} \sum_{n \leq N} |a_n|^2\right)^{k/2} \textbf{1}_{k \; \text{even}} \Bigg|^2 } \nonumber \\ & \leq \sum_{j=0}^{k} \frac{1}{2^k} {{k}\choose{j}} \nonumber \\ & \times \sqrt{ \mathbb{E}\Bigg| \int_{0}^{1} \left(\sum_{n \leq N} a_n f(n) e(n\theta) \right)^j \left(\overline{\sum_{n \leq N} a_n f(n) e(n\theta)} \right)^{k-j} - j! \left(\sum_{n \leq N} |a_n|^2 \right)^j \textbf{1}_{j=k-j} \Bigg|^2 } \nonumber \\ & \ll \sum_{j=0}^{k} \frac{1}{2^k} {{k}\choose{j}} \sqrt{ \frac{N^{k}}{N^{1/15k}} } = \sqrt{ \frac{N^{k}}{N^{1/15k}} }. \nonumber \end{align*} $$
Squaring both sides yields the second part of Probability Result 2.
To handle
![]() $\sum _{n \leq N} a_n f(n) \sin (2\pi n\theta )$
, one proceeds in the same way writing
$\sum _{n \leq N} a_n f(n) \sin (2\pi n\theta )$
, one proceeds in the same way writing
![]() $\sin (2\pi n\theta ) = \frac {e(n\theta ) - e(-n\theta )}{2i}$
, and noting that if k is even, then the term with
$\sin (2\pi n\theta ) = \frac {e(n\theta ) - e(-n\theta )}{2i}$
, and noting that if k is even, then the term with
![]() $j = k/2$
again produces a main term
$j = k/2$
again produces a main term
 $$ \begin{align*} \frac{1}{(2i)^k} {{k}\choose{k/2}} (-1)^{k/2} (k/2)! \left(\sum_{n \leq N} |a_n|^2\right)^{k/2} & = \frac{1}{2^k} {{k}\choose{k/2}} (k/2)! \left(\sum_{n \leq N} |a_n|^2 \right)^{k/2} \nonumber \\ & = \frac{k!}{(k/2)! 2^{k/2}} \left(\frac{1}{2} \sum_{n \leq N} |a_n|^2\right)^{k/2}. \nonumber \end{align*} $$
$$ \begin{align*} \frac{1}{(2i)^k} {{k}\choose{k/2}} (-1)^{k/2} (k/2)! \left(\sum_{n \leq N} |a_n|^2\right)^{k/2} & = \frac{1}{2^k} {{k}\choose{k/2}} (k/2)! \left(\sum_{n \leq N} |a_n|^2 \right)^{k/2} \nonumber \\ & = \frac{k!}{(k/2)! 2^{k/2}} \left(\frac{1}{2} \sum_{n \leq N} |a_n|^2\right)^{k/2}. \nonumber \end{align*} $$
In the Steinhaus case, the estimates we require cannot be read so immediately out of the work of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1], but we can extract suitable results by adapting their proofs.
Probability Result 3. Let
![]() $f(n)$
be a Steinhaus random multiplicative function. Then uniformly for any large N, any coefficients
$f(n)$
be a Steinhaus random multiplicative function. Then uniformly for any large N, any coefficients
![]() $(a_n)_{n \leq N}$
bounded in absolute value by 1, any
$(a_n)_{n \leq N}$
bounded in absolute value by 1, any
![]() $1 \leq k \leq c(\frac {\log N}{\log \log N})^{1/3}$
and any
$1 \leq k \leq c(\frac {\log N}{\log \log N})^{1/3}$
and any
![]() $0 \leq j \leq k$
, we have
$0 \leq j \leq k$
, we have
 $$ \begin{align*}& \mathbb{E}\Bigg| \int_{0}^{1} \!\left(\sum_{n \leq N} a_n f(n) \cos(2\pi n\theta) \!\right)^j \!\left(\overline{\sum_{n \leq N} a_n f(n) \cos(2\pi n\theta)} \!\right)^k d\theta - k! \!\left(\frac{1}{2} \sum_{n \leq N} |a_n|^2 \!\right)^k \!\textbf{1}_{j=k} \Bigg|^2\\ &\quad \ll \frac{N^{j+k}}{N^{1/15k}} ,\end{align*} $$
$$ \begin{align*}& \mathbb{E}\Bigg| \int_{0}^{1} \!\left(\sum_{n \leq N} a_n f(n) \cos(2\pi n\theta) \!\right)^j \!\left(\overline{\sum_{n \leq N} a_n f(n) \cos(2\pi n\theta)} \!\right)^k d\theta - k! \!\left(\frac{1}{2} \sum_{n \leq N} |a_n|^2 \!\right)^k \!\textbf{1}_{j=k} \Bigg|^2\\ &\quad \ll \frac{N^{j+k}}{N^{1/15k}} ,\end{align*} $$
where
![]() $\textbf {1}$
denotes the indicator function.
$\textbf {1}$
denotes the indicator function.
The same is true when
![]() $\sum _{n \leq N} a_n f(n) \cos (2\pi n\theta )$
is replaced by
$\sum _{n \leq N} a_n f(n) \cos (2\pi n\theta )$
is replaced by
![]() $\sum _{n \leq N} a_n f(n) \sin (2\pi n\theta )$
.
$\sum _{n \leq N} a_n f(n) \sin (2\pi n\theta )$
.
The proof of Probability Result 3 will rest on the following three Claims.
Claim 1. Let
![]() $N \in \mathbb {N}$
be large, let
$N \in \mathbb {N}$
be large, let
![]() $0 \leq j \leq J$
and
$0 \leq j \leq J$
and
![]() $1 \leq k \leq K$
, and let
$1 \leq k \leq K$
, and let
![]() $\mathcal {A}$
denote the set of all tuples
$\mathcal {A}$
denote the set of all tuples
![]() $(m_1, \ldots , m_J, n_1, \ldots , n_K) \in \{1, \ldots , N\}^{J+K}$
satisfying
$(m_1, \ldots , m_J, n_1, \ldots , n_K) \in \{1, \ldots , N\}^{J+K}$
satisfying
 $$ \begin{align*}\sum_{i=1}^{j} m_i - \sum_{i=j+1}^{J} m_i = \sum_{i=1}^{k} n_i - \sum_{i=k+1}^{K} n_i , \quad \text{and} \quad \prod_{i=1}^{J} m_i \cdot \prod_{i=1}^{K} n_i \; \text{is a square} .\end{align*} $$
$$ \begin{align*}\sum_{i=1}^{j} m_i - \sum_{i=j+1}^{J} m_i = \sum_{i=1}^{k} n_i - \sum_{i=k+1}^{K} n_i , \quad \text{and} \quad \prod_{i=1}^{J} m_i \cdot \prod_{i=1}^{K} n_i \; \text{is a square} .\end{align*} $$
Given such a tuple, let
![]() $\textbf {m}^{w}$
denote the weighted set obtained from
$\textbf {m}^{w}$
denote the weighted set obtained from
![]() $(m_1, \ldots , m_J)$
by counting each element m with weight
$(m_1, \ldots , m_J)$
by counting each element m with weight
![]() $w(m) = \#\{1 \leq i \leq j : m_i = m\} - \#\{j+1 \leq i \leq J : m_i = m\}$
(and discarding any elements whose weight turns out to be zero). Let
$w(m) = \#\{1 \leq i \leq j : m_i = m\} - \#\{j+1 \leq i \leq J : m_i = m\}$
(and discarding any elements whose weight turns out to be zero). Let
![]() $\textbf {n}^{w}$
denote the analogous weighted set obtained from
$\textbf {n}^{w}$
denote the analogous weighted set obtained from
![]() $(n_1, \ldots , n_K)$
.
$(n_1, \ldots , n_K)$
.
Then the number of tuples in
![]() $\mathcal {A}$
that do not satisfy
$\mathcal {A}$
that do not satisfy
![]() $\textbf {m}^{w} = \textbf {n}^{w}$
(i.e., equality of the elements of the sets and of their weights) is
$\textbf {m}^{w} = \textbf {n}^{w}$
(i.e., equality of the elements of the sets and of their weights) is
 $$ \begin{align*}\ll N^{(J+K)/2} \exp\left\{-\frac{\log N}{3(J+K)} + O((J+K)^2 (\log(J+K) + \log\log N))\right\} .\end{align*} $$
$$ \begin{align*}\ll N^{(J+K)/2} \exp\left\{-\frac{\log N}{3(J+K)} + O((J+K)^2 (\log(J+K) + \log\log N))\right\} .\end{align*} $$
Proof of Claim 1.
We can rearrange the conditions defining
![]() $\mathcal {A}$
into the form
$\mathcal {A}$
into the form
 $$ \begin{align*}\sum_{i=1}^{j} m_i + \sum_{i=k+1}^{K} n_i = \sum_{i=1}^{k} n_i + \sum_{i=j+1}^{J} m_i , \quad \text{and} \quad \prod_{i=1}^{J} m_i \cdot \prod_{i=1}^{K} n_i \; \text{is a square} .\end{align*} $$
$$ \begin{align*}\sum_{i=1}^{j} m_i + \sum_{i=k+1}^{K} n_i = \sum_{i=1}^{k} n_i + \sum_{i=j+1}^{J} m_i , \quad \text{and} \quad \prod_{i=1}^{J} m_i \cdot \prod_{i=1}^{K} n_i \; \text{is a square} .\end{align*} $$
And the relation
![]() $\textbf {m}^{w} = \textbf {n}^{w}$
is equivalent to saying that the tuple
$\textbf {m}^{w} = \textbf {n}^{w}$
is equivalent to saying that the tuple
![]() $(m_1, \ldots , m_j, n_{k+1}, \ldots , n_K)$
now occurring on the left is a permutation of the tuple
$(m_1, \ldots , m_j, n_{k+1}, \ldots , n_K)$
now occurring on the left is a permutation of the tuple
![]() $(n_1, \ldots , n_k, m_{j+1}, \ldots , m_J)$
on the right. So by Lemma 3.2 of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1] (writing the bound in the slightly more precise form from display (3.10) in their proof), the number of tuples in
$(n_1, \ldots , n_k, m_{j+1}, \ldots , m_J)$
on the right. So by Lemma 3.2 of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1] (writing the bound in the slightly more precise form from display (3.10) in their proof), the number of tuples in
![]() $\mathcal {A}$
with
$\mathcal {A}$
with
![]() $\textbf {m}^{w} \neq \textbf {n}^{w}$
is indeed
$\textbf {m}^{w} \neq \textbf {n}^{w}$
is indeed
 $$ \begin{align*}\ll N^{(J+K)/2} \exp\left\{-\frac{\log N}{3(J+K)} + O((J+K)^2 (\log(J+K) + \log\log N))\right\} .\end{align*} $$
$$ \begin{align*}\ll N^{(J+K)/2} \exp\left\{-\frac{\log N}{3(J+K)} + O((J+K)^2 (\log(J+K) + \log\log N))\right\} .\end{align*} $$
If we replace the condition that
![]() $\prod _{i=1}^{J} m_i \cdot \prod _{i=1}^{K} n_i$
is a square by the stronger condition that
$\prod _{i=1}^{J} m_i \cdot \prod _{i=1}^{K} n_i$
is a square by the stronger condition that
![]() $\prod _{i=1}^{J} m_i = \prod _{i=1}^{K} n_i$
, then we can obtain another relationship between
$\prod _{i=1}^{J} m_i = \prod _{i=1}^{K} n_i$
, then we can obtain another relationship between
![]() $(m_1, \ldots , m_J)$
and
$(m_1, \ldots , m_J)$
and
![]() $(n_1, \ldots , n_K)$
(for all except a small collection of tuples).
$(n_1, \ldots , n_K)$
(for all except a small collection of tuples).
Claim 2. Let
![]() $N \in \mathbb {N}$
be large, let
$N \in \mathbb {N}$
be large, let
![]() $0 \leq j \leq J$
and
$0 \leq j \leq J$
and
![]() $1 \leq k \leq K$
, and let
$1 \leq k \leq K$
, and let
![]() $\mathcal {B}$
denote the set of all tuples
$\mathcal {B}$
denote the set of all tuples
![]() $(m_1, \ldots , m_J, n_1, \ldots , n_K) \in \{1, \ldots , N\}^{J+K}$
satisfying
$(m_1, \ldots , m_J, n_1, \ldots , n_K) \in \{1, \ldots , N\}^{J+K}$
satisfying
 $$ \begin{align*}\sum_{i=1}^{j} m_i - \sum_{i=j+1}^{J} m_i = \sum_{i=1}^{k} n_i - \sum_{i=k+1}^{K} n_i , \quad \text{and} \quad \prod_{i=1}^{J} m_i = \prod_{i=1}^{K} n_i .\end{align*} $$
$$ \begin{align*}\sum_{i=1}^{j} m_i - \sum_{i=j+1}^{J} m_i = \sum_{i=1}^{k} n_i - \sum_{i=k+1}^{K} n_i , \quad \text{and} \quad \prod_{i=1}^{J} m_i = \prod_{i=1}^{K} n_i .\end{align*} $$
Then the number of tuples in
![]() $\mathcal {B}$
for which
$\mathcal {B}$
for which
![]() $(m_1, \ldots , m_J)$
is not a permutation of
$(m_1, \ldots , m_J)$
is not a permutation of
![]() $(n_1, \ldots , n_K)$
is
$(n_1, \ldots , n_K)$
is
![]() $\ll N^{(J+K)/2} \exp \{-\frac {\log N}{3(J+K)} + O((J+K)^2 (\log (J+K) + \log \log N))\}$
.
$\ll N^{(J+K)/2} \exp \{-\frac {\log N}{3(J+K)} + O((J+K)^2 (\log (J+K) + \log \log N))\}$
.
Proof of Claim 2.
Since any tuple in
![]() $\mathcal {B}$
also belongs to the set
$\mathcal {B}$
also belongs to the set
![]() $\mathcal {A}$
from Claim 1, we may restrict attention to tuples satisfying
$\mathcal {A}$
from Claim 1, we may restrict attention to tuples satisfying
![]() $\textbf {m}^{w} = \textbf {n}^{w}$
. We shall analyse these by investigating the number s of common elements (counted with multiplicity) between the multisets
$\textbf {m}^{w} = \textbf {n}^{w}$
. We shall analyse these by investigating the number s of common elements (counted with multiplicity) between the multisets
![]() $\{m_1, \ldots , m_j\}$
and
$\{m_1, \ldots , m_j\}$
and
![]() $\{m_{j+1}, \ldots , m_J\}$
, and the number t of common elements between
$\{m_{j+1}, \ldots , m_J\}$
, and the number t of common elements between
![]() $\{n_1, \ldots , n_k\}$
and
$\{n_1, \ldots , n_k\}$
and
![]() $\{n_{k+1}, \ldots , n_K\}$
. If
$\{n_{k+1}, \ldots , n_K\}$
. If
![]() $s=t=0$
, then the relation
$s=t=0$
, then the relation
![]() $\textbf {m}^{w} = \textbf {n}^{w}$
implies that
$\textbf {m}^{w} = \textbf {n}^{w}$
implies that
![]() $(m_1, \ldots , m_J)$
is a permutation of
$(m_1, \ldots , m_J)$
is a permutation of
![]() $(n_1, \ldots , n_K)$
, so we may ignore this case and assume that
$(n_1, \ldots , n_K)$
, so we may ignore this case and assume that
![]() $s+t \geq 1$
.
$s+t \geq 1$
.
After possibly reordering some of the
![]() $m_i$
and
$m_i$
and
![]() $n_i$
(which at worst will multiply our final bounds by an acceptable factor of
$n_i$
(which at worst will multiply our final bounds by an acceptable factor of
![]() $(J+K)!$
), we may assume that
$(J+K)!$
), we may assume that
![]() $m_i = m_{j+i}$
for all
$m_i = m_{j+i}$
for all
![]() $1 \leq i \leq s$
and that
$1 \leq i \leq s$
and that
![]() $n_i = n_{k+i}$
for all
$n_i = n_{k+i}$
for all
![]() $1 \leq i \leq t$
. This leaves
$1 \leq i \leq t$
. This leaves
![]() $J+K-2(s+t)$
other components of
$J+K-2(s+t)$
other components of
![]() $(m_1, \ldots , m_J, n_1, \ldots , n_K)$
. The relation
$(m_1, \ldots , m_J, n_1, \ldots , n_K)$
. The relation
![]() $\textbf {m}^{w} = \textbf {n}^{w}$
implies these
$\textbf {m}^{w} = \textbf {n}^{w}$
implies these
![]() $J+K-2(s+t)$
latter components must consist of
$J+K-2(s+t)$
latter components must consist of
![]() $(1/2)(J+K-2(s+t))$
components
$(1/2)(J+K-2(s+t))$
components
![]() $m_i$
(for which there are
$m_i$
(for which there are
![]() $\leq N^{(J+K)/2 - s - t}$
possibilities), and
$\leq N^{(J+K)/2 - s - t}$
possibilities), and
![]() $(1/2)(J+K-2(s+t))$
components
$(1/2)(J+K-2(s+t))$
components
![]() $n_i$
that are a permutation of the
$n_i$
that are a permutation of the
![]() $m_i$
. Meanwhile, note that
$m_i$
. Meanwhile, note that
 $$ \begin{align*}\textbf{m}^{w} = \textbf{n}^{w} \quad \text{and} \quad \prod_{i=1}^{J} m_i = \prod_{i=1}^{K} n_i \quad \Rightarrow \quad \prod_{i=1}^{s} m_i^2 = \prod_{i=1}^{t} n_i^2 \quad \Rightarrow \quad \prod_{i=1}^{s} m_i = \prod_{i=1}^{t} n_i .\end{align*} $$
$$ \begin{align*}\textbf{m}^{w} = \textbf{n}^{w} \quad \text{and} \quad \prod_{i=1}^{J} m_i = \prod_{i=1}^{K} n_i \quad \Rightarrow \quad \prod_{i=1}^{s} m_i^2 = \prod_{i=1}^{t} n_i^2 \quad \Rightarrow \quad \prod_{i=1}^{s} m_i = \prod_{i=1}^{t} n_i .\end{align*} $$
Then standard calculations with iterated divisor functions
![]() $d_{\alpha }(\cdot )$
(see, for example, Section 3.1 of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1]) show the number of possibilities for
$d_{\alpha }(\cdot )$
(see, for example, Section 3.1 of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1]) show the number of possibilities for
![]() $m_1, \ldots , m_s, n_1, \ldots , n_t$
is
$m_1, \ldots , m_s, n_1, \ldots , n_t$
is
 $$ \begin{align*} & \leq \min\left\{\sum_{m_1, \ldots, m_s \leq N} d_{t}(m_1 ... m_s) , \sum_{n_1, \ldots, n_t \leq N} d_{s}(n_1 ... n_t) \right\} \nonumber \\ & \leq \min\left\{\left(\sum_{m \leq N} d_{t}(m)\right)^s , \left(\sum_{n \leq N} d_{s}(n) \right)^t \right\} \\ &\leq N^{\min\{s,t\}} (2\log N)^{st} \leq N^{\min\{s,t\}} (2\log N)^{(J+K)^2}. \nonumber \end{align*} $$
$$ \begin{align*} & \leq \min\left\{\sum_{m_1, \ldots, m_s \leq N} d_{t}(m_1 ... m_s) , \sum_{n_1, \ldots, n_t \leq N} d_{s}(n_1 ... n_t) \right\} \nonumber \\ & \leq \min\left\{\left(\sum_{m \leq N} d_{t}(m)\right)^s , \left(\sum_{n \leq N} d_{s}(n) \right)^t \right\} \\ &\leq N^{\min\{s,t\}} (2\log N)^{st} \leq N^{\min\{s,t\}} (2\log N)^{(J+K)^2}. \nonumber \end{align*} $$
So for given s and t, our total number of possible tuples is
 $$ \begin{align*} &\leq (J+K)! \cdot N^{(J+K)/2 - s - t} \cdot N^{\min\{s,t\}} (2\log N)^{(J+K)^2} \\ &\leq N^{(J+K)/2 - \max\{s,t\}} e^{O((J+K)\log(J+K) + (J+K)^2 \log\log N)} .\end{align*} $$
$$ \begin{align*} &\leq (J+K)! \cdot N^{(J+K)/2 - s - t} \cdot N^{\min\{s,t\}} (2\log N)^{(J+K)^2} \\ &\leq N^{(J+K)/2 - \max\{s,t\}} e^{O((J+K)\log(J+K) + (J+K)^2 \log\log N)} .\end{align*} $$
Summing over all
![]() $s+t \geq 1$
gives a more than acceptable final contribution.
$s+t \geq 1$
gives a more than acceptable final contribution.
We shall also require a slightly more complicated ‘doubled up’ version of Claim 2.
Claim 3. Let
![]() $N \in \mathbb {N}$
be large, let
$N \in \mathbb {N}$
be large, let
![]() $0 \leq j \leq J$
and
$0 \leq j \leq J$
and
![]() $1 \leq k \leq K$
, and let
$1 \leq k \leq K$
, and let
![]() $\mathcal {C}$
denote the set of all tuples
$\mathcal {C}$
denote the set of all tuples
![]() $(m_1^{(1)}, \ldots , m_J^{(1)}, n_1^{(1)}, \ldots , n_K^{(1)}, m_1^{(2)}, \ldots , m_J^{(2)}, n_1^{(2)}, \ldots , n_K^{(2)}) \in \{1, \ldots , N\}^{2(J+K)}$
satisfying
$(m_1^{(1)}, \ldots , m_J^{(1)}, n_1^{(1)}, \ldots , n_K^{(1)}, m_1^{(2)}, \ldots , m_J^{(2)}, n_1^{(2)}, \ldots , n_K^{(2)}) \in \{1, \ldots , N\}^{2(J+K)}$
satisfying
 $$ \begin{align*} & \sum_{i=1}^{j} m_i^{(l)} - \sum_{i=j+1}^{J} m_i^{(l)} \\ & \quad = \sum_{i=1}^{k} n_i^{(l)} - \sum_{i=k+1}^{K} n_i^{(l)} \quad \forall l \in \{1,2\} , \quad \text{and} \quad \prod_{i=1}^{J} m_i^{(1)} \cdot \prod_{i=1}^{K} n_i^{(2)} = \prod_{i=1}^{J} m_i^{(2)} \cdot \prod_{i=1}^{K} n_i^{(1)} .\end{align*} $$
$$ \begin{align*} & \sum_{i=1}^{j} m_i^{(l)} - \sum_{i=j+1}^{J} m_i^{(l)} \\ & \quad = \sum_{i=1}^{k} n_i^{(l)} - \sum_{i=k+1}^{K} n_i^{(l)} \quad \forall l \in \{1,2\} , \quad \text{and} \quad \prod_{i=1}^{J} m_i^{(1)} \cdot \prod_{i=1}^{K} n_i^{(2)} = \prod_{i=1}^{J} m_i^{(2)} \cdot \prod_{i=1}^{K} n_i^{(1)} .\end{align*} $$
Then the number of tuples in
![]() $\mathcal {C}$
for which
$\mathcal {C}$
for which
![]() $(m_1^{(1)}, \ldots , m_J^{(1)})$
is not a permutation of
$(m_1^{(1)}, \ldots , m_J^{(1)})$
is not a permutation of
![]() $(n_1^{(1)}, \ldots , n_K^{(1)})$
, or
$(n_1^{(1)}, \ldots , n_K^{(1)})$
, or
![]() $(m_1^{(2)}, \ldots , m_J^{(2)})$
is not a permutation of
$(m_1^{(2)}, \ldots , m_J^{(2)})$
is not a permutation of
![]() $(n_1^{(2)}, \ldots , n_K^{(2)})$
, is
$(n_1^{(2)}, \ldots , n_K^{(2)})$
, is
![]() $\ll N^{J+K} \exp \{-\frac {\log N}{6(J+K)} + O((J+K)^2 (\log (J+K) + \log \log N))\}$
.
$\ll N^{J+K} \exp \{-\frac {\log N}{6(J+K)} + O((J+K)^2 (\log (J+K) + \log \log N))\}$
.
Proof of Claim 3.
With an obvious adaptation of the notation from Claim 1, we may restrict attention to tuples in
![]() $\mathcal {C}$
that satisfy
$\mathcal {C}$
that satisfy
![]() $\textbf {m}^{(1)w} = \textbf {n}^{(1)w}$
and
$\textbf {m}^{(1)w} = \textbf {n}^{(1)w}$
and
![]() $\textbf {m}^{(2)w} = \textbf {n}^{(2)w}$
. For if there is some element whose weight is (say) greater in
$\textbf {m}^{(2)w} = \textbf {n}^{(2)w}$
. For if there is some element whose weight is (say) greater in
![]() $\textbf {m}^{(1)}$
than in
$\textbf {m}^{(1)}$
than in
![]() $\textbf {n}^{(1)}$
, and whose weight is at least as great in
$\textbf {n}^{(1)}$
, and whose weight is at least as great in
![]() $\textbf {m}^{(2)}$
as in
$\textbf {m}^{(2)}$
as in
![]() $\textbf {n}^{(2)}$
, then (adding our equationsFootnote
3
for
$\textbf {n}^{(2)}$
, then (adding our equationsFootnote
3
for
![]() $l=1,2$
), we get
$l=1,2$
), we get
 $$ \begin{align*}\sum_{i=1}^{j} m_i^{(1)} + \sum_{i=1}^{j} m_i^{(2)} - \sum_{i=j+1}^{J} m_i^{(1)} - \sum_{i=j+1}^{J} m_i^{(2)} = \sum_{i=1}^{k} n_i^{(1)} + \sum_{i=1}^{k} n_i^{(2)} - \sum_{i=k+1}^{K} n_i^{(1)} - \sum_{i=k+1}^{K} n_i^{(2)} ,\end{align*} $$
$$ \begin{align*}\sum_{i=1}^{j} m_i^{(1)} + \sum_{i=1}^{j} m_i^{(2)} - \sum_{i=j+1}^{J} m_i^{(1)} - \sum_{i=j+1}^{J} m_i^{(2)} = \sum_{i=1}^{k} n_i^{(1)} + \sum_{i=1}^{k} n_i^{(2)} - \sum_{i=k+1}^{K} n_i^{(1)} - \sum_{i=k+1}^{K} n_i^{(2)} ,\end{align*} $$
 $$ \begin{align*}\text{and} \quad \prod_{i=1}^{J} m_i^{(1)} \cdot \prod_{i=1}^{J} m_i^{(2)} \cdot \prod_{i=1}^{K} n_i^{(1)} \cdot \prod_{i=1}^{K} n_i^{(2)} \; \text{is a square} ,\end{align*} $$
$$ \begin{align*}\text{and} \quad \prod_{i=1}^{J} m_i^{(1)} \cdot \prod_{i=1}^{J} m_i^{(2)} \cdot \prod_{i=1}^{K} n_i^{(1)} \cdot \prod_{i=1}^{K} n_i^{(2)} \; \text{is a square} ,\end{align*} $$
where the weighted set corresponding to the concatenated tuple of m terms on the left will be unequal to the weighted set corresponding to the n terms on the right. Thus, Claim 1 implies that the number of such ‘bad’ tuples is
![]() $\ll N^{J+K} \exp \{-\frac {\log N}{6(J+K)} + O((J+K)^2 (\log (J+K) + \log \log N))\}$
.
$\ll N^{J+K} \exp \{-\frac {\log N}{6(J+K)} + O((J+K)^2 (\log (J+K) + \log \log N))\}$
.
For those ‘good’ tuples where
![]() $\textbf {m}^{(1)w} = \textbf {n}^{(1)w}$
and
$\textbf {m}^{(1)w} = \textbf {n}^{(1)w}$
and
![]() $\textbf {m}^{(2)w} = \textbf {n}^{(2)w}$
, we may conclude similarly as in the proof of Claim 2. Thus, if
$\textbf {m}^{(2)w} = \textbf {n}^{(2)w}$
, we may conclude similarly as in the proof of Claim 2. Thus, if
![]() $s^{(1)}$
denotes the number of common elements (counted with multiplicity) between
$s^{(1)}$
denotes the number of common elements (counted with multiplicity) between
![]() $\{m_1^{(1)}, \ldots , m_j^{(1)}\}$
and
$\{m_1^{(1)}, \ldots , m_j^{(1)}\}$
and
![]() $\{m_{j+1}^{(1)}, \ldots , m_J^{(1)}\}$
, similarly for
$\{m_{j+1}^{(1)}, \ldots , m_J^{(1)}\}$
, similarly for
![]() $t^{(1)}, s^{(2)}, t^{(2)}$
, then we may ignore the case where all of these are zero, and otherwise our total number of possible tuples is
$t^{(1)}, s^{(2)}, t^{(2)}$
, then we may ignore the case where all of these are zero, and otherwise our total number of possible tuples is
 $$ \begin{align*} & \ll (2(J+K))! \cdot N^{(J+K)/2 - s^{(1)} - t^{(1)}} N^{(J+K)/2 - s^{(2)} - t^{(2)}} \\ &\quad \cdot N^{\min\{s^{(1)} + t^{(2)}, s^{(2)} + t^{(1)}\}} (2\log N)^{(s^{(1)} + t^{(2)})(s^{(2)} + t^{(1)})} \nonumber \\ & \ll N^{J+K- \max\{s^{(1)} + t^{(2)}, s^{(2)} + t^{(1)}\}} e^{O((J+K)\log(J+K) + (J+K)^2 \log\log N)}. \nonumber \end{align*} $$
$$ \begin{align*} & \ll (2(J+K))! \cdot N^{(J+K)/2 - s^{(1)} - t^{(1)}} N^{(J+K)/2 - s^{(2)} - t^{(2)}} \\ &\quad \cdot N^{\min\{s^{(1)} + t^{(2)}, s^{(2)} + t^{(1)}\}} (2\log N)^{(s^{(1)} + t^{(2)})(s^{(2)} + t^{(1)})} \nonumber \\ & \ll N^{J+K- \max\{s^{(1)} + t^{(2)}, s^{(2)} + t^{(1)}\}} e^{O((J+K)\log(J+K) + (J+K)^2 \log\log N)}. \nonumber \end{align*} $$
Summing this over all
![]() $s^{(1)} + t^{(1)} + s^{(2)} + t^{(2)} \geq 1$
gives an acceptable contribution.
$s^{(1)} + t^{(1)} + s^{(2)} + t^{(2)} \geq 1$
gives an acceptable contribution.
Proof of Probability Result 3.
Writing
![]() $\cos (2\pi n\theta ) = \frac {e(n\theta ) + e(-n\theta )}{2}$
, and attempting to mimic the proof of the Steinhaus case of Theorem 1.1 of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1], one finds that in place of the linear equations
$\cos (2\pi n\theta ) = \frac {e(n\theta ) + e(-n\theta )}{2}$
, and attempting to mimic the proof of the Steinhaus case of Theorem 1.1 of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1], one finds that in place of the linear equations
![]() $\sum _{i=1}^{j} m_i = \sum _{i=1}^{k} n_i$
that they encounter, we must handle the more general situation where some of the
$\sum _{i=1}^{j} m_i = \sum _{i=1}^{k} n_i$
that they encounter, we must handle the more general situation where some of the
![]() $m_i$
and
$m_i$
and
![]() $n_i$
come with negative signs (arising from the
$n_i$
come with negative signs (arising from the
![]() $e(-n\theta )$
terms). Using Claims 2 and 3 in place of Lemma 3.3 and Corollary 3.5 of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1], one can bound all the ‘off-diagonal’ contributions with the same quality bounds as Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1]. Thus, it only remains to check that the diagonal contribution to the integral in Probability Result 3 (coming when
$e(-n\theta )$
terms). Using Claims 2 and 3 in place of Lemma 3.3 and Corollary 3.5 of Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1], one can bound all the ‘off-diagonal’ contributions with the same quality bounds as Benatar, Nishry and Rodgers [Reference Benatar, Nishry and Rodgers1]. Thus, it only remains to check that the diagonal contribution to the integral in Probability Result 3 (coming when
![]() $j=k$
, from summands in
$j=k$
, from summands in
![]() $\left (\sum _{n \leq N} a_n f(n) \cos (2\pi n\theta ) \right )^k$
that are a permutation of the summands in
$\left (\sum _{n \leq N} a_n f(n) \cos (2\pi n\theta ) \right )^k$
that are a permutation of the summands in
![]() $\left (\overline {\sum _{n \leq N} a_n f(n) \cos (2\pi n\theta )} \right )^k$
) is acceptably close to
$\left (\overline {\sum _{n \leq N} a_n f(n) \cos (2\pi n\theta )} \right )^k$
) is acceptably close to
![]() $k! (\frac {1}{2} \sum _{n \leq N} |a_n|^2)^k$
.
$k! (\frac {1}{2} \sum _{n \leq N} |a_n|^2)^k$
.
But we can write that diagonal contribution as
 $$ \begin{align*} & k! \sum_{n_1, \ldots, n_k \leq N} |a_{n_1}|^2 ... |a_{n_k}|^2 \int_{0}^{1} \cos^{2}(2\pi n_1 \theta) ... \cos^{2}(2\pi n_k \theta) d\theta \\ &\quad + O\Bigg( k! \sum_{\substack{n_1, \ldots, n_k \leq N, \\ n_i \; \text{not all distinct}}} |a_{n_1}|^2 ... |a_{n_k}|^2 \Bigg) .\end{align*} $$
$$ \begin{align*} & k! \sum_{n_1, \ldots, n_k \leq N} |a_{n_1}|^2 ... |a_{n_k}|^2 \int_{0}^{1} \cos^{2}(2\pi n_1 \theta) ... \cos^{2}(2\pi n_k \theta) d\theta \\ &\quad + O\Bigg( k! \sum_{\substack{n_1, \ldots, n_k \leq N, \\ n_i \; \text{not all distinct}}} |a_{n_1}|^2 ... |a_{n_k}|^2 \Bigg) .\end{align*} $$
Since
![]() $\cos ^{2}(2\pi n\theta ) = \frac {1}{2} + \frac {e(2n\theta )}{4} + \frac {e(-2n\theta )}{4}$
, we have
$\cos ^{2}(2\pi n\theta ) = \frac {1}{2} + \frac {e(2n\theta )}{4} + \frac {e(-2n\theta )}{4}$
, we have
![]() $\int _{0}^{1} \cos ^{2}(2\pi n_1 \theta ) ... \cos ^{2}(2\pi n_k \theta ) d\theta = 1/2^k$
(coming from the term
$\int _{0}^{1} \cos ^{2}(2\pi n_1 \theta ) ... \cos ^{2}(2\pi n_k \theta ) d\theta = 1/2^k$
(coming from the term
![]() $1/2$
in the expansion of all the factors
$1/2$
in the expansion of all the factors
![]() $\cos ^{2}(2\pi n_j \theta )$
) except for tuples
$\cos ^{2}(2\pi n_j \theta )$
) except for tuples
![]() $n_1, \ldots , n_k$
satisfying additional linear relations (producing additional contributions from a product of terms
$n_1, \ldots , n_k$
satisfying additional linear relations (producing additional contributions from a product of terms
![]() $\frac {e(2n_j \theta )}{4} , \frac {e(-2n_j \theta )}{4}$
). The total of all such additional contributions, together with the ‘big Oh’ term
$\frac {e(2n_j \theta )}{4} , \frac {e(-2n_j \theta )}{4}$
). The total of all such additional contributions, together with the ‘big Oh’ term
 $O\Bigg ( k! \sum _{\substack {n_1, \ldots , n_k \leq N, \\ n_i \; \text {not all distinct}}} |a_{n_1}|^2 ... |a_{n_k}|^2 \Bigg )$
, is
$O\Bigg ( k! \sum _{\substack {n_1, \ldots , n_k \leq N, \\ n_i \; \text {not all distinct}}} |a_{n_1}|^2 ... |a_{n_k}|^2 \Bigg )$
, is
![]() $\ll k! k^2 N^{k-1} .$
$\ll k! k^2 N^{k-1} .$
In order to bring Probability Results 2 and 3 to bear, we must show that averages of Dirichlet characters behave similarly to averages of random multiplicative functions. When averaging over all characters mod q, this will be straightforward (provided we keep sufficient control on the lengths of the sums being averaged) thanks to orthogonality of characters. When averaging only over Legendre symbols
![]() $\left (\frac {\cdot }{q}\right )$
with q prime, matters are more subtle, and connected with the distribution of zeros of Dirichlet L-functions. Nevertheless, there are various approaches that can be applied – for example, using the explicit formula for character sums over primes along with results of Siegel and Linnik type on exceptional zeros and (log-free) zero density. Since we will arrange our arguments so that only upper bounds (rather than asymptotic equalities) for character averages are needed, we instead proceed in a different way using the sieve, which will allow quantitatively stronger conclusions about the density of
$\left (\frac {\cdot }{q}\right )$
with q prime, matters are more subtle, and connected with the distribution of zeros of Dirichlet L-functions. Nevertheless, there are various approaches that can be applied – for example, using the explicit formula for character sums over primes along with results of Siegel and Linnik type on exceptional zeros and (log-free) zero density. Since we will arrange our arguments so that only upper bounds (rather than asymptotic equalities) for character averages are needed, we instead proceed in a different way using the sieve, which will allow quantitatively stronger conclusions about the density of
![]() $\mathcal {P}_{H}$
in Theorem 3.
$\mathcal {P}_{H}$
in Theorem 3.
Number Theory Result 3 (See Lemma 9 of Montgomery and Vaughan [Reference Montgomery and Vaughan16], 1979).
Let
![]() $f(n)$
be an extended Rademacher random multiplicative function. Then uniformly for any large Q, any
$f(n)$
be an extended Rademacher random multiplicative function. Then uniformly for any large Q, any
![]() $N \leq Q$
, and any complex coefficients
$N \leq Q$
, and any complex coefficients
![]() $(\alpha _n)_{n \leq N}$
, we have
$(\alpha _n)_{n \leq N}$
, we have
 $$ \begin{align*} \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{prime}}} \left| \sum_{n \leq N} \alpha_n \left(\frac{n}{q}\right) \right|^2 & \ll \mathbb{E}\left| \sum_{n \leq N} \alpha_n f(n) \right|^2 + \frac{1}{Q^{0.99}} \Bigg( \sum_{n \leq N} |\alpha_n| \sqrt{s(n)} \Bigg)^2 \nonumber \\ & \ll \mathbb{E}\left| \sum_{n \leq N} \alpha_n f(n) \right|^2 + \frac{N}{Q^{0.99}} \Bigg( \sum_{n \leq N} |\alpha_n| \Bigg)^2 , \nonumber \end{align*} $$
$$ \begin{align*} \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{prime}}} \left| \sum_{n \leq N} \alpha_n \left(\frac{n}{q}\right) \right|^2 & \ll \mathbb{E}\left| \sum_{n \leq N} \alpha_n f(n) \right|^2 + \frac{1}{Q^{0.99}} \Bigg( \sum_{n \leq N} |\alpha_n| \sqrt{s(n)} \Bigg)^2 \nonumber \\ & \ll \mathbb{E}\left| \sum_{n \leq N} \alpha_n f(n) \right|^2 + \frac{N}{Q^{0.99}} \Bigg( \sum_{n \leq N} |\alpha_n| \Bigg)^2 , \nonumber \end{align*} $$
say, where
![]() $s(n)$
denotes the squarefree part of n (i.e., n divided by its largest square factor).
$s(n)$
denotes the squarefree part of n (i.e., n divided by its largest square factor).
Proof of Number Theory Result 3.
This result is very close to Lemma 9 of Montgomery and Vaughan [Reference Montgomery and Vaughan16], and would follow by tweaking the argument in Lemmas 4–9 of their paper. For convenience, and since it is neat and fairly short, we outline a self-contained proof here.
Note first that if q is prime and
![]() $n \leq q$
, then
$n \leq q$
, then
![]() $\left (\frac {n}{q}\right ) = \left (\frac {s(n)}{q}\right )$
, where
$\left (\frac {n}{q}\right ) = \left (\frac {s(n)}{q}\right )$
, where
![]() $s(n)$
denotes the squarefree part of n. So we can rewrite
$s(n)$
denotes the squarefree part of n. So we can rewrite
![]() $\sum _{n \leq N} \alpha _n \left (\frac {n}{q}\right ) = \sum _{\substack {s \leq N, \\ s \; \text {squarefree}}} \left (\frac {s}{q}\right ) \sum _{\substack {n \leq N, \\ s(n) = s}} \alpha _n$
. We also always have
$\sum _{n \leq N} \alpha _n \left (\frac {n}{q}\right ) = \sum _{\substack {s \leq N, \\ s \; \text {squarefree}}} \left (\frac {s}{q}\right ) \sum _{\substack {n \leq N, \\ s(n) = s}} \alpha _n$
. We also always have
![]() $f(n) = f(s(n))$
, so it is easy to see that
$f(n) = f(s(n))$
, so it is easy to see that
 $$ \begin{align*}\mathbb{E}\left| \sum_{n \leq N} \alpha_n f(n) \right|^2 = \mathbb{E}\Bigg| \sum_{\substack{s \leq N, \\ s \; \text{squarefree}}} f(s) \sum_{\substack{n \leq N, \\ s(n) = s}} \alpha_n \Bigg|^2 = \sum_{\substack{s \leq N, \\ s \; \text{squarefree}}} \Bigg| \sum_{\substack{n \leq N, \\ s(n) = s}} \alpha_n \Bigg|^2 .\end{align*} $$
$$ \begin{align*}\mathbb{E}\left| \sum_{n \leq N} \alpha_n f(n) \right|^2 = \mathbb{E}\Bigg| \sum_{\substack{s \leq N, \\ s \; \text{squarefree}}} f(s) \sum_{\substack{n \leq N, \\ s(n) = s}} \alpha_n \Bigg|^2 = \sum_{\substack{s \leq N, \\ s \; \text{squarefree}}} \Bigg| \sum_{\substack{n \leq N, \\ s(n) = s}} \alpha_n \Bigg|^2 .\end{align*} $$
To execute the proof, the only (possibly) non-obvious step is the introduction of upper bound sieve weights in place of the sum over primes q. At the level of precision we are seeking, we have much flexibility in our choice of sieve. For example (following the notation of Section 3.2 of Montgomery and Vaughan’s book [Reference Montgomery and Vaughan17] with
![]() $z = Q^{0.005}$
and
$z = Q^{0.005}$
and
![]() $P = \prod _{\text {primes} \; p \leq Q^{0.005}} p$
), we can use Selberg sieve weights
$P = \prod _{\text {primes} \; p \leq Q^{0.005}} p$
), we can use Selberg sieve weights
![]() $\lambda _e = \lambda _{e}^{+}$
satisfying
$\lambda _e = \lambda _{e}^{+}$
satisfying
![]() $\lambda _e = 0$
whenever
$\lambda _e = 0$
whenever
![]() $e> Q^{0.01}$
, and
$e> Q^{0.01}$
, and
![]() $\sum _{e} |\lambda _e| \ll \frac {Q^{0.01}}{\log ^{2}Q}$
, and
$\sum _{e} |\lambda _e| \ll \frac {Q^{0.01}}{\log ^{2}Q}$
, and
![]() $\sum _{e|q} \lambda _e \geq \textbf {1}_{p|q \Rightarrow p> Q^{0.005}}$
for all q, and
$\sum _{e|q} \lambda _e \geq \textbf {1}_{p|q \Rightarrow p> Q^{0.005}}$
for all q, and
![]() $\sum _{Q \leq q \leq 2Q} \sum _{e|q} \lambda _e \ll \frac {Q}{\log Q}$
. Thus, we have
$\sum _{Q \leq q \leq 2Q} \sum _{e|q} \lambda _e \ll \frac {Q}{\log Q}$
. Thus, we have
 $$ \begin{align*} & \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{prime}}} \left| \sum_{n \leq N} \alpha_n \left(\frac{n}{q}\right) \right|^2 \\ &\quad \leq \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{odd}}} (\sum_{e|q} \lambda_e ) \Bigg| \sum_{\substack{s \leq N, \\ s \; \text{squarefree}}} \left(\frac{s}{q}\right) \sum_{\substack{n \leq N, \\ s(n) = s}} \alpha_n \Bigg|^2 \nonumber \\ &\quad = \sum_{\substack{s_1 , s_2 \leq N, \\ \text{squarefree}}} (\sum_{\substack{n \leq N, \\ s(n) = s_1}} \alpha_n) \overline{(\sum_{\substack{n \leq N, \\ s(n) = s_2}} \alpha_n)} \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{odd}}} (\sum_{e|q} \lambda_e ) \left(\frac{s_1 s_2}{q}\right). \nonumber \end{align*} $$
$$ \begin{align*} & \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{prime}}} \left| \sum_{n \leq N} \alpha_n \left(\frac{n}{q}\right) \right|^2 \\ &\quad \leq \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{odd}}} (\sum_{e|q} \lambda_e ) \Bigg| \sum_{\substack{s \leq N, \\ s \; \text{squarefree}}} \left(\frac{s}{q}\right) \sum_{\substack{n \leq N, \\ s(n) = s}} \alpha_n \Bigg|^2 \nonumber \\ &\quad = \sum_{\substack{s_1 , s_2 \leq N, \\ \text{squarefree}}} (\sum_{\substack{n \leq N, \\ s(n) = s_1}} \alpha_n) \overline{(\sum_{\substack{n \leq N, \\ s(n) = s_2}} \alpha_n)} \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{odd}}} (\sum_{e|q} \lambda_e ) \left(\frac{s_1 s_2}{q}\right). \nonumber \end{align*} $$
Here,
![]() $\left (\frac {s}{q}\right )$
should be understood to mean the Jacobi symbol, which is well defined for all odd q and all s, and agrees with the Legendre symbol when q is prime. See Section 9.3 of Montgomery and Vaughan’s book [Reference Montgomery and Vaughan17], for example.
$\left (\frac {s}{q}\right )$
should be understood to mean the Jacobi symbol, which is well defined for all odd q and all s, and agrees with the Legendre symbol when q is prime. See Section 9.3 of Montgomery and Vaughan’s book [Reference Montgomery and Vaughan17], for example.
The contribution from the diagonal summands
![]() $s_1 = s_2$
is
$s_1 = s_2$
is
 $$ \begin{align*} &\sum_{\substack{s \leq N, \\ \text{squarefree}}} \Bigg|\sum_{\substack{n \leq N, \\ s(n) = s}} \alpha_n \Bigg|^2 \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{odd}}} \left(\sum_{e|q} \lambda_e \right) \left(\frac{s^2}{q}\right) \\&\quad \leq \sum_{\substack{s \leq N, \\ \text{squarefree}}} \Bigg|\sum_{\substack{n \leq N, \\ s(n) = s}} \alpha_n \Bigg|^2 \frac{\log Q}{Q} \sum_{Q \leq q \leq 2Q} \left(\sum_{e|q} \lambda_e \right) \nonumber \\&\quad \ll \sum_{\substack{s \leq N, \\ \text{squarefree}}} |\sum_{\substack{n \leq N, \\ s(n) = s}} \alpha_n |^2 = \mathbb{E}\Bigg| \sum_{n \leq N} \alpha_n f(n) \Bigg|^2 , \nonumber \end{align*} $$
$$ \begin{align*} &\sum_{\substack{s \leq N, \\ \text{squarefree}}} \Bigg|\sum_{\substack{n \leq N, \\ s(n) = s}} \alpha_n \Bigg|^2 \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{odd}}} \left(\sum_{e|q} \lambda_e \right) \left(\frac{s^2}{q}\right) \\&\quad \leq \sum_{\substack{s \leq N, \\ \text{squarefree}}} \Bigg|\sum_{\substack{n \leq N, \\ s(n) = s}} \alpha_n \Bigg|^2 \frac{\log Q}{Q} \sum_{Q \leq q \leq 2Q} \left(\sum_{e|q} \lambda_e \right) \nonumber \\&\quad \ll \sum_{\substack{s \leq N, \\ \text{squarefree}}} |\sum_{\substack{n \leq N, \\ s(n) = s}} \alpha_n |^2 = \mathbb{E}\Bigg| \sum_{n \leq N} \alpha_n f(n) \Bigg|^2 , \nonumber \end{align*} $$
which is acceptable.
If
![]() $s_1 \neq s_2$
are squarefree, then
$s_1 \neq s_2$
are squarefree, then
![]() $s_1 s_2$
is not a perfect square, and so the mapping
$s_1 s_2$
is not a perfect square, and so the mapping
![]() $q \mapsto \left (\frac {s_1 s_2}{q}\right )$
is a non-principal Dirichlet character of conductor at most
$q \mapsto \left (\frac {s_1 s_2}{q}\right )$
is a non-principal Dirichlet character of conductor at most
![]() $4s_1 s_2$
. Hence, we can bound the contribution from
$4s_1 s_2$
. Hence, we can bound the contribution from
![]() $s_1 \neq s_2$
by
$s_1 \neq s_2$
by
 $$ \begin{align*} & \frac{\log Q}{Q} \sum_{\substack{e \leq Q^{0.01}, \\ e \; \text{odd}}} |\lambda_e| \sum_{\substack{s_1 \neq s_2 \leq N, \\ \text{squarefree}}} |\sum_{\substack{n \leq N, \\ s(n) = s_1}} \alpha_n| |\sum_{\substack{n \leq N, \\ s(n) = s_2}} \alpha_n | \Bigg|\sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{odd}, \\ e|q}} \left(\frac{s_1 s_2}{q}\right) \Bigg| \nonumber \\ & \ll \frac{\log Q}{Q} \sum_{\substack{e \leq Q^{0.01} , \\ e \; \text{odd}}} |\lambda_e| \sum_{\substack{s_1 \neq s_2 \leq N, \\ \text{squarefree}}} |\sum_{\substack{n \leq N, \\ s(n) = s_1}} \alpha_n| |\sum_{\substack{n \leq N, \\ s(n) = s_2}} \alpha_n | \sqrt{s_1 s_2} \log(s_1 s_2) , \nonumber \end{align*} $$
$$ \begin{align*} & \frac{\log Q}{Q} \sum_{\substack{e \leq Q^{0.01}, \\ e \; \text{odd}}} |\lambda_e| \sum_{\substack{s_1 \neq s_2 \leq N, \\ \text{squarefree}}} |\sum_{\substack{n \leq N, \\ s(n) = s_1}} \alpha_n| |\sum_{\substack{n \leq N, \\ s(n) = s_2}} \alpha_n | \Bigg|\sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{odd}, \\ e|q}} \left(\frac{s_1 s_2}{q}\right) \Bigg| \nonumber \\ & \ll \frac{\log Q}{Q} \sum_{\substack{e \leq Q^{0.01} , \\ e \; \text{odd}}} |\lambda_e| \sum_{\substack{s_1 \neq s_2 \leq N, \\ \text{squarefree}}} |\sum_{\substack{n \leq N, \\ s(n) = s_1}} \alpha_n| |\sum_{\substack{n \leq N, \\ s(n) = s_2}} \alpha_n | \sqrt{s_1 s_2} \log(s_1 s_2) , \nonumber \end{align*} $$
where the second line follows using the Pólya–Vinogradov inequality (see, for example, Section 9.4 of Montgomery and Vaughan [Reference Montgomery and Vaughan17]) and a little manipulation. (Note that because we switched to sums with sieve weights rather than sums over primes, here we finally obtained character sums over (essentially) all integers q in an interval, for which we have the strong Pólya–Vinogradov bound.) Since our weights
![]() $\lambda _e$
satisfy
$\lambda _e$
satisfy
![]() $\sum _{e} |\lambda _e| \ll \frac {Q^{0.01}}{\log ^{2}Q}$
, one can check that this expression is also acceptably small.
$\sum _{e} |\lambda _e| \ll \frac {Q^{0.01}}{\log ^{2}Q}$
, one can check that this expression is also acceptably small.
6 Proof of Theorem 3
In this section, we shall prove Theorem 3, our positive ‘almost all’ result for real characters. The proof splits into four parts: first, we shall reduce the problem to one about the distribution of sufficiently short exponential sums (this part will also be applicable when handling the complex case in Theorem 4); second, we show that it will suffice to bound mean square averages (over characters) of moment related objects involving those exponential sums; third, we perform a technical ‘netting’ step allowing us to treat
![]() $q/H(q)$
as constant on dyadic ranges
$q/H(q)$
as constant on dyadic ranges
![]() $Q \leq q \leq 2Q$
, so that we can perform the desired averages over q (this is only needed in the real case); and finally, we complete the analysis using Probability Result 2 and Number Theory Result 3.
$Q \leq q \leq 2Q$
, so that we can perform the desired averages over q (this is only needed in the real case); and finally, we complete the analysis using Probability Result 2 and Number Theory Result 3.
6.1 Reduction to short partial Fourier series
If
![]() $\chi $
is an even non-principal Dirichlet character mod q (so that
$\chi $
is an even non-principal Dirichlet character mod q (so that
![]() $\chi (-1)=1$
, and therefore
$\chi (-1)=1$
, and therefore
![]() $\chi (-k) = \chi (k)$
for all k), then we can rewrite the Pólya Fourier expansion (3.1) in the form
$\chi (-k) = \chi (k)$
for all k), then we can rewrite the Pólya Fourier expansion (3.1) in the form
 $$ \begin{align*} &\frac{S_{\chi, H}(X)}{\sqrt{H}} \\ & = \frac{\tau(\chi)}{2\pi i \sqrt{H}} \sum_{1 \leq k < q/2} \frac{\overline{\chi}(k)}{k} \left(e(\frac{kX}{q}) (e(kH/q) - 1) - e(-\frac{kX}{q}) (e(-kH/q) - 1) \right) + O(\frac{\log q}{\sqrt{H}}) \nonumber \\ & = \frac{\tau(\chi)}{\pi \sqrt{H}} \sum_{1 \leq k < q/2} \frac{\overline{\chi}(k)}{k} \left(\sin(2\pi k(X+H)/q) - \sin(2\pi k X/q) \right) + O(\frac{\log q}{\sqrt{H}}) \nonumber \\ & = \frac{2\tau(\chi)}{\pi \sqrt{H}} \sum_{1 \leq k < q/2} \frac{\overline{\chi}(k) \sin(\pi k H/q)}{k} \cos(\pi k (2X+H)/q) + O(\frac{\log q}{\sqrt{H}}). \nonumber \end{align*} $$
$$ \begin{align*} &\frac{S_{\chi, H}(X)}{\sqrt{H}} \\ & = \frac{\tau(\chi)}{2\pi i \sqrt{H}} \sum_{1 \leq k < q/2} \frac{\overline{\chi}(k)}{k} \left(e(\frac{kX}{q}) (e(kH/q) - 1) - e(-\frac{kX}{q}) (e(-kH/q) - 1) \right) + O(\frac{\log q}{\sqrt{H}}) \nonumber \\ & = \frac{\tau(\chi)}{\pi \sqrt{H}} \sum_{1 \leq k < q/2} \frac{\overline{\chi}(k)}{k} \left(\sin(2\pi k(X+H)/q) - \sin(2\pi k X/q) \right) + O(\frac{\log q}{\sqrt{H}}) \nonumber \\ & = \frac{2\tau(\chi)}{\pi \sqrt{H}} \sum_{1 \leq k < q/2} \frac{\overline{\chi}(k) \sin(\pi k H/q)}{k} \cos(\pi k (2X+H)/q) + O(\frac{\log q}{\sqrt{H}}). \nonumber \end{align*} $$
The sum over k here would be too long for our subsequent calculations, in particular to allow the computation of its high moments. However, if
![]() $1 \leq k_1 , k_2 < q/2$
and if
$1 \leq k_1 , k_2 < q/2$
and if
![]() $X \in \{0,1,\ldots ,q-1\}$
is uniformly random, then we have
$X \in \{0,1,\ldots ,q-1\}$
is uniformly random, then we have
![]() $\mathbb {E} \cos (\pi k_1 (2X+H)/q) \cos (\pi k_2 (2X+H)/q) = (1/2) \textbf {1}_{k_1 = k_2}$
, and so
$\mathbb {E} \cos (\pi k_1 (2X+H)/q) \cos (\pi k_2 (2X+H)/q) = (1/2) \textbf {1}_{k_1 = k_2}$
, and so
 $$ \begin{align*} & \mathbb{E}\left| \frac{2\tau(\chi)}{\pi \sqrt{H}} \sum_{(q/H)\log(q/H) \leq k < q/2} \frac{\overline{\chi}(k) \sin(\pi k H/q)}{k} \cos(\pi k (2X+H)/q) \right|^2 \nonumber \\ & = \frac{2q}{\pi^2 H} \sum_{(q/H)\log(q/H) \leq k < q/2} \frac{\sin^{2}(\pi k H/q)}{k^2} \ll \frac{1}{\log(q/H)} , \nonumber \end{align*} $$
$$ \begin{align*} & \mathbb{E}\left| \frac{2\tau(\chi)}{\pi \sqrt{H}} \sum_{(q/H)\log(q/H) \leq k < q/2} \frac{\overline{\chi}(k) \sin(\pi k H/q)}{k} \cos(\pi k (2X+H)/q) \right|^2 \nonumber \\ & = \frac{2q}{\pi^2 H} \sum_{(q/H)\log(q/H) \leq k < q/2} \frac{\sin^{2}(\pi k H/q)}{k^2} \ll \frac{1}{\log(q/H)} , \nonumber \end{align*} $$
which tends to zero as
![]() $q \rightarrow \infty $
under the conditions of Theorem 3 (or Theorem 4). It follows that the part of the sum with
$q \rightarrow \infty $
under the conditions of Theorem 3 (or Theorem 4). It follows that the part of the sum with
![]() $k \geq (q/H)\log (q/H)$
tends to zero in probability, for any choice of
$k \geq (q/H)\log (q/H)$
tends to zero in probability, for any choice of
![]() $\chi $
, so may be ignored in our investigation of the limiting distribution.
$\chi $
, so may be ignored in our investigation of the limiting distribution.
The form of the function
![]() $\cos (\pi k (2X+H)/q)$
, with
$\cos (\pi k (2X+H)/q)$
, with
![]() $X \in \{0,1,\ldots ,q-1\}$
uniformly random, is a bit ungainly. However, under the conditions of Theorems 3 and 4, it turns out we can replace this by
$X \in \{0,1,\ldots ,q-1\}$
uniformly random, is a bit ungainly. However, under the conditions of Theorems 3 and 4, it turns out we can replace this by
![]() $\cos (2 \pi k \theta )$
, where
$\cos (2 \pi k \theta )$
, where
![]() $\theta \in [0,1]$
is uniformly random. Indeed, if
$\theta \in [0,1]$
is uniformly random. Indeed, if
![]() $X \in \{0,1,\ldots ,q-1\}$
, then for any
$X \in \{0,1,\ldots ,q-1\}$
, then for any
![]() $\theta \in [\frac {X + H/2}{q} - \frac {1}{2q}, \frac {X + H/2}{q} + \frac {1}{2q}]$
mod 1, we get
$\theta \in [\frac {X + H/2}{q} - \frac {1}{2q}, \frac {X + H/2}{q} + \frac {1}{2q}]$
mod 1, we get
 $$ \begin{align*} & \left| \frac{2\tau(\chi)}{\pi \sqrt{H}} \sum_{1 \leq k < (q/H)\log(q/H)} \frac{\overline{\chi}(k) \sin(\pi k H/q)}{k} (\cos(\pi k (2X + H)/q) - \cos(2\pi k\theta)) \right| \nonumber \\ & \ll \frac{\sqrt{q}}{\sqrt{H}} \sum_{1 \leq k < (q/H)\log(q/H)} \frac{|\sin(\pi k H/q)|}{k} \cdot \frac{k}{q} \ll \frac{(q/H)^{3/2} \log(q/H)}{q} , \nonumber \end{align*} $$
$$ \begin{align*} & \left| \frac{2\tau(\chi)}{\pi \sqrt{H}} \sum_{1 \leq k < (q/H)\log(q/H)} \frac{\overline{\chi}(k) \sin(\pi k H/q)}{k} (\cos(\pi k (2X + H)/q) - \cos(2\pi k\theta)) \right| \nonumber \\ & \ll \frac{\sqrt{q}}{\sqrt{H}} \sum_{1 \leq k < (q/H)\log(q/H)} \frac{|\sin(\pi k H/q)|}{k} \cdot \frac{k}{q} \ll \frac{(q/H)^{3/2} \log(q/H)}{q} , \nonumber \end{align*} $$
which tends to zero (deterministically) as
![]() $q \rightarrow \infty $
. Here, we mildly use our assumption that
$q \rightarrow \infty $
. Here, we mildly use our assumption that
![]() $\frac {\log (q/H)}{\log q} \rightarrow 0$
as
$\frac {\log (q/H)}{\log q} \rightarrow 0$
as
![]() $q \rightarrow \infty $
. Since choosing
$q \rightarrow \infty $
. Since choosing
![]() $X \in \{0,1,\ldots ,q-1\}$
uniformly at random, and then choosing
$X \in \{0,1,\ldots ,q-1\}$
uniformly at random, and then choosing
![]() $\theta \in [\frac {X + H/2}{q} - \frac {1}{2q}, \frac {X + H/2}{q} + \frac {1}{2q}]$
mod 1 uniformly at random, is exactly the same thing as choosing
$\theta \in [\frac {X + H/2}{q} - \frac {1}{2q}, \frac {X + H/2}{q} + \frac {1}{2q}]$
mod 1 uniformly at random, is exactly the same thing as choosing
![]() $\theta \in [0,1]$
uniformly at random, we only need to consider the latter process.
$\theta \in [0,1]$
uniformly at random, we only need to consider the latter process.
In summary, for even characters
![]() $\chi $
, it will suffice to prove Theorem 3 (and Theorem 4) with
$\chi $
, it will suffice to prove Theorem 3 (and Theorem 4) with
![]() $S_{\chi , H}(X)/\sqrt {H}$
replaced by
$S_{\chi , H}(X)/\sqrt {H}$
replaced by
 $$ \begin{align*}\frac{2\tau(\chi)}{\pi \sqrt{H}} \sum_{1 \leq k < (q/H)\log(q/H)} \frac{\overline{\chi}(k) \sin(\pi k H/q)}{k} \cos(2\pi k\theta) , \quad \theta \sim \text{Uni}[0,1] .\end{align*} $$
$$ \begin{align*}\frac{2\tau(\chi)}{\pi \sqrt{H}} \sum_{1 \leq k < (q/H)\log(q/H)} \frac{\overline{\chi}(k) \sin(\pi k H/q)}{k} \cos(2\pi k\theta) , \quad \theta \sim \text{Uni}[0,1] .\end{align*} $$
For odd characters
![]() $\chi $
, where
$\chi $
, where
![]() $\chi (-1)=-1$
and therefore
$\chi (-1)=-1$
and therefore
![]() $\chi (-k) = -\chi (k)$
for all k, one similarly ends up with
$\chi (-k) = -\chi (k)$
for all k, one similarly ends up with
![]() $\frac {2 \tau (\chi )}{\pi i \sqrt {H}} \sum _{1 \leq k < (q/H)\log (q/H)} \frac {\overline {\chi }(k) \sin (\pi k H/q)}{k} \sin (2\pi k\theta )$
. The treatment of either sum will be exactly similar, so for simplicity, we shall focus on the cosine case. Note that we need not distinguish between even and odd characters in our subsequent calculations because if
$\frac {2 \tau (\chi )}{\pi i \sqrt {H}} \sum _{1 \leq k < (q/H)\log (q/H)} \frac {\overline {\chi }(k) \sin (\pi k H/q)}{k} \sin (2\pi k\theta )$
. The treatment of either sum will be exactly similar, so for simplicity, we shall focus on the cosine case. Note that we need not distinguish between even and odd characters in our subsequent calculations because if
![]() $\frac {2\tau (\chi )}{\pi \sqrt {H}} \sum _{1 \leq k < (q/H)\log (q/H)} \frac {\overline {\chi }(k) \sin (\pi k H/q)}{k} \cos (2\pi k\theta )$
has the desired Gaussian limiting distribution for ‘almost all’ choices of
$\frac {2\tau (\chi )}{\pi \sqrt {H}} \sum _{1 \leq k < (q/H)\log (q/H)} \frac {\overline {\chi }(k) \sin (\pi k H/q)}{k} \cos (2\pi k\theta )$
has the desired Gaussian limiting distribution for ‘almost all’ choices of
![]() $\chi $
(in the sense of Theorems 3 and 4), then, in particular, it has the desired limiting distribution for almost all choices of even
$\chi $
(in the sense of Theorems 3 and 4), then, in particular, it has the desired limiting distribution for almost all choices of even
![]() $\chi $
, similarly for
$\chi $
, similarly for
![]() $\frac {2 \tau (\chi )}{\pi i \sqrt {H}} \sum _{1 \leq k < (q/H)\log (q/H)} \frac {\overline {\chi }(k) \sin (\pi k H/q)}{k} \sin (2\pi k\theta )$
.
$\frac {2 \tau (\chi )}{\pi i \sqrt {H}} \sum _{1 \leq k < (q/H)\log (q/H)} \frac {\overline {\chi }(k) \sin (\pi k H/q)}{k} \sin (2\pi k\theta )$
.
Note also that when
![]() $\chi = \left (\frac {\cdot }{q}\right )$
is real, one has
$\chi = \left (\frac {\cdot }{q}\right )$
is real, one has
![]() $\tau (\chi ) = \sqrt {q}$
if
$\tau (\chi ) = \sqrt {q}$
if
![]() $\chi $
is even (which occurs when
$\chi $
is even (which occurs when
![]() $q \equiv 1$
mod 4), and one has
$q \equiv 1$
mod 4), and one has
![]() $\tau (\chi ) = i\sqrt {q}$
if
$\tau (\chi ) = i\sqrt {q}$
if
![]() $\chi $
is odd (which occurs when
$\chi $
is odd (which occurs when
![]() $q \equiv 3$
mod 4). See chapter 9.3 of Montgomery and Vaughan [Reference Montgomery and Vaughan17]. Inserting these expressions above, we see that when proving Theorem 3, we can work with
$q \equiv 3$
mod 4). See chapter 9.3 of Montgomery and Vaughan [Reference Montgomery and Vaughan17]. Inserting these expressions above, we see that when proving Theorem 3, we can work with
 $$ \begin{align} \frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{1 \leq k < (q/H)\log(q/H)} \frac{\overline{\chi}(k) \sin(\pi k H/q)}{k} \cos(2\pi k\theta) , \quad \theta \sim \text{Uni}[0,1] \end{align} $$
$$ \begin{align} \frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{1 \leq k < (q/H)\log(q/H)} \frac{\overline{\chi}(k) \sin(\pi k H/q)}{k} \cos(2\pi k\theta) , \quad \theta \sim \text{Uni}[0,1] \end{align} $$
and with
![]() $\frac {2 \sqrt {q}}{\pi \sqrt {H}} \sum _{1 \leq k < (q/H)\log (q/H)} \frac {\overline {\chi }(k) \sin (\pi k H/q)}{k} \sin (2\pi k\theta )$
. These sums are visibly real-valued when
$\frac {2 \sqrt {q}}{\pi \sqrt {H}} \sum _{1 \leq k < (q/H)\log (q/H)} \frac {\overline {\chi }(k) \sin (\pi k H/q)}{k} \sin (2\pi k\theta )$
. These sums are visibly real-valued when
![]() $\chi $
is real. And, in fact, we are free to work with these sums when proving Theorem 4 as well, where we know that
$\chi $
is real. And, in fact, we are free to work with these sums when proving Theorem 4 as well, where we know that
![]() $|\tau (\chi )| = \sqrt {q}$
, but it is harder to say a lot about the argument of
$|\tau (\chi )| = \sqrt {q}$
, but it is harder to say a lot about the argument of
![]() $\tau (\chi )$
. That is because in Theorem 4, the target distribution
$\tau (\chi )$
. That is because in Theorem 4, the target distribution
![]() $Z_1 + iZ_2$
is rotationally invariant, so if this is the limiting distribution of, for example, (6.1) for ‘almost all’ choices of
$Z_1 + iZ_2$
is rotationally invariant, so if this is the limiting distribution of, for example, (6.1) for ‘almost all’ choices of
![]() $\chi $
, then it remains the limiting distribution of
$\chi $
, then it remains the limiting distribution of
![]() $\frac {2\tau (\chi )}{\pi \sqrt {H}} \sum _{1 \leq k < (q/H)\log (q/H)} \frac {\overline {\chi }(k) \sin (\pi k H/q)}{k} \cos (2\pi k\theta )$
for the same
$\frac {2\tau (\chi )}{\pi \sqrt {H}} \sum _{1 \leq k < (q/H)\log (q/H)} \frac {\overline {\chi }(k) \sin (\pi k H/q)}{k} \cos (2\pi k\theta )$
for the same
![]() $\chi $
.
$\chi $
.
6.2 Working with moments
The method of moments for proving distributional convergence is discussed in a general context in, for example, chapter 5.8.4 of Gut [Reference Gut8]. In particular, our
![]() $N(0,1)$
target distribution is determined by its moments, which are
$N(0,1)$
target distribution is determined by its moments, which are
![]() $\mathbb {E} N(0,1)^j = (1/\sqrt {2\pi }) \int _{-\infty }^{\infty } z^j e^{-z^{2}/2} dz = \textbf {1}_{j \; \text {even}} \frac {j!}{2^{j/2} (j/2)!}$
, where
$\mathbb {E} N(0,1)^j = (1/\sqrt {2\pi }) \int _{-\infty }^{\infty } z^j e^{-z^{2}/2} dz = \textbf {1}_{j \; \text {even}} \frac {j!}{2^{j/2} (j/2)!}$
, where
![]() $\textbf {1}$
denotes the indicator function. So in view of (6.1), to prove Theorem 3, it would suffice to show that there exists a subsequence
$\textbf {1}$
denotes the indicator function. So in view of (6.1), to prove Theorem 3, it would suffice to show that there exists a subsequence
![]() $\mathcal {P}_{H}$
of primes, with the density claimed in the theorem, such that for all
$\mathcal {P}_{H}$
of primes, with the density claimed in the theorem, such that for all
![]() $j \in \mathbb {N}$
, we have
$j \in \mathbb {N}$
, we have
 $$ \begin{align*} &\int_{0}^{1} \left( \frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{1 \leq k < (q/H)\log(q/H)} \frac{\left(\frac{k}{q}\right) \sin(\pi k H/q)}{k} \cos(2\pi k\theta) \right)^{j} d\theta \rightarrow \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} \quad \\ &\quad \text{as } q \rightarrow \infty , \; q \in \mathcal{P}_{H} .\end{align*} $$
$$ \begin{align*} &\int_{0}^{1} \left( \frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{1 \leq k < (q/H)\log(q/H)} \frac{\left(\frac{k}{q}\right) \sin(\pi k H/q)}{k} \cos(2\pi k\theta) \right)^{j} d\theta \rightarrow \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} \quad \\ &\quad \text{as } q \rightarrow \infty , \; q \in \mathcal{P}_{H} .\end{align*} $$
(Actually, we must also prove this for
![]() $\frac {2 \sqrt {q}}{\pi \sqrt {H}} \sum _{1 \leq k < (q/H)\log (q/H)} \frac {\left (\frac {k}{q}\right ) \sin (\pi k H/q)}{k} \sin (2\pi k\theta )$
, but this will be exactly similar to the cosine case, so we shall only discuss the latter.)
$\frac {2 \sqrt {q}}{\pi \sqrt {H}} \sum _{1 \leq k < (q/H)\log (q/H)} \frac {\left (\frac {k}{q}\right ) \sin (\pi k H/q)}{k} \sin (2\pi k\theta )$
, but this will be exactly similar to the cosine case, so we shall only discuss the latter.)
Rewriting slightly, if we set
![]() $a_k = a_{k,q,H} := \frac {q \sin (\pi k H/q)}{\pi H k}$
, then we want to show the existence of
$a_k = a_{k,q,H} := \frac {q \sin (\pi k H/q)}{\pi H k}$
, then we want to show the existence of
![]() $\mathcal {P}_{H}$
such that, for each fixed
$\mathcal {P}_{H}$
such that, for each fixed
![]() $j \in \mathbb {N}$
, we have
$j \in \mathbb {N}$
, we have
 $$ \begin{align*} &\left(\frac{4H}{q} \right)^{j/2} \left| \int_{0}^{1} \left( \sum_{k < \frac{q}{H} \log(q/H)} a_k \left(\frac{k}{q}\right) \cos(2\pi k\theta) \right)^{j} d\theta - \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} (\frac{q}{4H})^{j/2} \right| \rightarrow 0 \quad \\ &\quad \text{as } q \rightarrow \infty , \; q \in \mathcal{P}_{H} .\end{align*} $$
$$ \begin{align*} &\left(\frac{4H}{q} \right)^{j/2} \left| \int_{0}^{1} \left( \sum_{k < \frac{q}{H} \log(q/H)} a_k \left(\frac{k}{q}\right) \cos(2\pi k\theta) \right)^{j} d\theta - \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} (\frac{q}{4H})^{j/2} \right| \rightarrow 0 \quad \\ &\quad \text{as } q \rightarrow \infty , \; q \in \mathcal{P}_{H} .\end{align*} $$
Here, the coefficients
![]() $a_k$
are real, bounded in absolute value by 1 (thanks to the estimate
$a_k$
are real, bounded in absolute value by 1 (thanks to the estimate
![]() $|\sin x| \leq |x|$
), and satisfy
$|\sin x| \leq |x|$
), and satisfy
 $$ \begin{align*}\frac{1}{2} \sum_{k < (q/H)\log(q/H)} |a_k|^2 & = \frac{q^2}{2\pi^2 H^2} \sum_{1 \leq k < (q/H)\log(q/H)} \frac{\sin^2(\frac{\pi k H}{q})}{k^2} \\ &= \frac{q^2}{4\pi^2 H^2} \sum_{1 \leq |k| < (q/H)\log(q/H)} \frac{\sin^2(\frac{\pi k H}{q})}{k^2} ,\end{align*} $$
$$ \begin{align*}\frac{1}{2} \sum_{k < (q/H)\log(q/H)} |a_k|^2 & = \frac{q^2}{2\pi^2 H^2} \sum_{1 \leq k < (q/H)\log(q/H)} \frac{\sin^2(\frac{\pi k H}{q})}{k^2} \\ &= \frac{q^2}{4\pi^2 H^2} \sum_{1 \leq |k| < (q/H)\log(q/H)} \frac{\sin^2(\frac{\pi k H}{q})}{k^2} ,\end{align*} $$
since
![]() $\frac {\sin ^2(\pi k H/q)}{k^2}$
is an even function of k. Using the fact that
$\frac {\sin ^2(\pi k H/q)}{k^2}$
is an even function of k. Using the fact that
![]() $|\sin (\pi k H/q)| = (1/2)|e(k H/2q) - e(- k H/2q)| = (1/2)|e(k H/q) - 1|$
, we can rewrite this further as
$|\sin (\pi k H/q)| = (1/2)|e(k H/2q) - e(- k H/2q)| = (1/2)|e(k H/q) - 1|$
, we can rewrite this further as
 $$ \begin{align*} &\frac{q^2}{16 \pi^2 H^2} \sum_{1 \leq |k| < (q/H)\log(q/H)} \frac{|e(\frac{k H}{q}) - 1|^2}{k^2} \\ & = \frac{q^2}{16 \pi^2 H^2} \Bigg(\sum_{1 \leq |k| < q/2} \frac{|e(\frac{k H}{q}) - 1|^2}{k^2} + O(\frac{1}{(q/H)\log(q/H)}) \Bigg) \nonumber \\ & = \frac{q}{4H} \Bigg( 1 + O(\frac{1}{\log(q/H)}) \Bigg) , \nonumber \end{align*} $$
$$ \begin{align*} &\frac{q^2}{16 \pi^2 H^2} \sum_{1 \leq |k| < (q/H)\log(q/H)} \frac{|e(\frac{k H}{q}) - 1|^2}{k^2} \\ & = \frac{q^2}{16 \pi^2 H^2} \Bigg(\sum_{1 \leq |k| < q/2} \frac{|e(\frac{k H}{q}) - 1|^2}{k^2} + O(\frac{1}{(q/H)\log(q/H)}) \Bigg) \nonumber \\ & = \frac{q}{4H} \Bigg( 1 + O(\frac{1}{\log(q/H)}) \Bigg) , \nonumber \end{align*} $$
where the final equality uses the calculation of
![]() $\frac {q}{(2\pi )^2} \sum _{0 < |k| < q/2} \frac {1}{k^2} |e(kH/q) - 1|^2$
that we performed in Section 3.
$\frac {q}{(2\pi )^2} \sum _{0 < |k| < q/2} \frac {1}{k^2} |e(kH/q) - 1|^2$
that we performed in Section 3.
To finish the proof, for each
![]() $Q = 2^r, r \in \mathbb {N}$
, we would like to show that the averages
$Q = 2^r, r \in \mathbb {N}$
, we would like to show that the averages
 $$ \begin{align*}&\frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{prime}}} \left(\frac{4H}{q} \right)^{j} \\ & \left| \int_{0}^{1} \Bigg( \sum_{k < \frac{q\log(q/H)}{H}} a_k \left(\frac{k}{q}\right) \cos(2\pi k\theta) \Bigg)^{j} d\theta - \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} \Bigg(\frac{1}{2} \sum_{k < \frac{q\log(q/H)}{H}} |a_k|^2 \Bigg)^{j/2} \right|^2\end{align*} $$
$$ \begin{align*}&\frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{prime}}} \left(\frac{4H}{q} \right)^{j} \\ & \left| \int_{0}^{1} \Bigg( \sum_{k < \frac{q\log(q/H)}{H}} a_k \left(\frac{k}{q}\right) \cos(2\pi k\theta) \Bigg)^{j} d\theta - \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} \Bigg(\frac{1}{2} \sum_{k < \frac{q\log(q/H)}{H}} |a_k|^2 \Bigg)^{j/2} \right|^2\end{align*} $$
are ‘small’, implying that the number of ‘bad’ primes
![]() $Q \leq q \leq 2Q$
where the summand is large is also small. Unfortunately, as
$Q \leq q \leq 2Q$
where the summand is large is also small. Unfortunately, as
![]() $Q \leq q \leq 2Q$
varies, it is not only the character
$Q \leq q \leq 2Q$
varies, it is not only the character
![]() $\chi (k) = \left (\frac {k}{q}\right )$
(which we expect to behave like an extended Rademacher random multiplicative function
$\chi (k) = \left (\frac {k}{q}\right )$
(which we expect to behave like an extended Rademacher random multiplicative function
![]() $f(k)$
) that varies here, but also many other terms like
$f(k)$
) that varies here, but also many other terms like
![]() $\sqrt {q}/\sqrt {H}$
,
$\sqrt {q}/\sqrt {H}$
,
![]() $\sin (\pi k H/q)$
, and the length of the sum over k. In other words, the coefficients
$\sin (\pi k H/q)$
, and the length of the sum over k. In other words, the coefficients
![]() $a_k = a_{k,q,H}$
may depend a priori on
$a_k = a_{k,q,H}$
may depend a priori on
![]() $q/H(q)$
as well as on k. Notice this issue will not arise in the non-real case of Theorem 4, where we can average over all characters
$q/H(q)$
as well as on k. Notice this issue will not arise in the non-real case of Theorem 4, where we can average over all characters
![]() $\chi $
mod q whilst holding q, and therefore
$\chi $
mod q whilst holding q, and therefore
![]() $H(q)$
and everything else, fixed.
$H(q)$
and everything else, fixed.
6.3 Controlling the behaviour of
 $q/H$
$q/H$
To get around the problem just discussed, we will apply a ‘netting’ argument to the given function
![]() $H(q)$
. Given
$H(q)$
. Given
![]() $Q = 2^r, r \in \mathbb {N}$
, let us define the small quantity
$Q = 2^r, r \in \mathbb {N}$
, let us define the small quantity
![]() $\eta = \eta _{H,Q}> 0$
by
$\eta = \eta _{H,Q}> 0$
by
![]() $\eta := \frac {1}{\min _{Q \leq q \leq 2Q} \log (q/H(q))}$
, say, and then define a family of functions
$\eta := \frac {1}{\min _{Q \leq q \leq 2Q} \log (q/H(q))}$
, say, and then define a family of functions
![]() $H_{n} : [Q,2Q] \rightarrow \mathbb {R}$
in the following way:
$H_{n} : [Q,2Q] \rightarrow \mathbb {R}$
in the following way:
For each
![]() $Q \leq q \leq 2Q$
, there exists some
$Q \leq q \leq 2Q$
, there exists some
![]() $n = n(q)$
for which
$n = n(q)$
for which
![]() $q/H_{n}(q) \leq q/H(q) \leq e^{\eta } q/H_{n}(q)$
, and then
$q/H_{n}(q) \leq q/H(q) \leq e^{\eta } q/H_{n}(q)$
, and then
 $$ \begin{align*} & \int_{0}^{1} \Bigg| \frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{1 \leq k < (q/H)\log(q/H)} \frac{\left(\frac{k}{q}\right) \sin(\pi k H/q)}{k} \cos(2\pi k\theta) - \nonumber \\ & - \frac{2\sqrt{q}}{\pi \sqrt{H_n}} \sum_{1 \leq k < (q/H_n)\log(q/H_n)} \frac{\left(\frac{k}{q}\right) \sin(\pi k H_n /q)}{k} \cos(2\pi k\theta) \Bigg|^2 d\theta \nonumber \\ & = \frac{2}{\pi^2} \sum_{1 \leq k < (q/H_n)\log(q/H_n)} \frac{1}{k^2} |\frac{\sqrt{q}}{\sqrt{H}} \sin(\pi k H /q) - \frac{\sqrt{q}}{\sqrt{H_n}} \sin(\pi k H_n /q)|^2 + O(\frac{1}{\log(q/H)}) \nonumber \\ & \ll \sum_{1 \leq k < (q/H_n)\log(q/H_n)} \frac{1}{k^2} \min\left\{\frac{(\eta k)^2}{(q/H)}, q/H \right\} + \frac{1}{\log(q/H)} \ll \eta , \nonumber \end{align*} $$
$$ \begin{align*} & \int_{0}^{1} \Bigg| \frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{1 \leq k < (q/H)\log(q/H)} \frac{\left(\frac{k}{q}\right) \sin(\pi k H/q)}{k} \cos(2\pi k\theta) - \nonumber \\ & - \frac{2\sqrt{q}}{\pi \sqrt{H_n}} \sum_{1 \leq k < (q/H_n)\log(q/H_n)} \frac{\left(\frac{k}{q}\right) \sin(\pi k H_n /q)}{k} \cos(2\pi k\theta) \Bigg|^2 d\theta \nonumber \\ & = \frac{2}{\pi^2} \sum_{1 \leq k < (q/H_n)\log(q/H_n)} \frac{1}{k^2} |\frac{\sqrt{q}}{\sqrt{H}} \sin(\pi k H /q) - \frac{\sqrt{q}}{\sqrt{H_n}} \sin(\pi k H_n /q)|^2 + O(\frac{1}{\log(q/H)}) \nonumber \\ & \ll \sum_{1 \leq k < (q/H_n)\log(q/H_n)} \frac{1}{k^2} \min\left\{\frac{(\eta k)^2}{(q/H)}, q/H \right\} + \frac{1}{\log(q/H)} \ll \eta , \nonumber \end{align*} $$
where the final line uses the fact that
![]() $\frac {d}{dt} \sqrt {t} \sin (\pi k/t) \ll \frac {k}{t^{3/2}}$
for large t. The assumptions of Theorem 3 imply that
$\frac {d}{dt} \sqrt {t} \sin (\pi k/t) \ll \frac {k}{t^{3/2}}$
for large t. The assumptions of Theorem 3 imply that
![]() $\eta \rightarrow 0$
as
$\eta \rightarrow 0$
as
![]() $Q \rightarrow \infty $
, and so the difference between (6.1) and the analogous sum involving
$Q \rightarrow \infty $
, and so the difference between (6.1) and the analogous sum involving
![]() $H_n$
tends to zero in probability, uniformly for
$H_n$
tends to zero in probability, uniformly for
![]() $Q \leq q \leq 2Q$
.
$Q \leq q \leq 2Q$
.
Consequently, when proving Theorem 3, it will suffice to work with the particular functions
![]() $H_n(q)$
, which have the property that
$H_n(q)$
, which have the property that
![]() $q/H_{n}(q) = Q/H_{n}(Q)$
is constant for all
$q/H_{n}(q) = Q/H_{n}(Q)$
is constant for all
![]() $Q \leq q \leq 2Q$
. More precisely: it will suffice to prove that for each
$Q \leq q \leq 2Q$
. More precisely: it will suffice to prove that for each
and for all
 $$ \begin{align*}1 \leq j \leq \min\{\frac{\log^{1/4}(Q/H_{n}(Q))}{50}, \frac{\log Q}{4\log(Q/H_{n}(Q))}\} ,\end{align*} $$
$$ \begin{align*}1 \leq j \leq \min\{\frac{\log^{1/4}(Q/H_{n}(Q))}{50}, \frac{\log Q}{4\log(Q/H_{n}(Q))}\} ,\end{align*} $$
say, we have
 $$ \begin{align} & \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{prime}}} \nonumber\\ &\quad \left| \int_{0}^{1} \Bigg( \sum_{k < \frac{q\log(q/H_n)}{H_n}} a_k \left(\frac{k}{q}\right) \cos(2\pi k\theta) \Bigg)^{j} d\theta - \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} \Bigg(\frac{1}{2} \sum_{k < \frac{q\log(q/H_n)}{H_n}} |a_k|^2 \Bigg)^{j/2} \right|^2 \nonumber \\ & \ll \left(\frac{Q}{4H_{n}(Q)} \right)^{j} e^{-2\log^{3/4}(Q/H_{n}(Q))}. \end{align} $$
$$ \begin{align} & \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{prime}}} \nonumber\\ &\quad \left| \int_{0}^{1} \Bigg( \sum_{k < \frac{q\log(q/H_n)}{H_n}} a_k \left(\frac{k}{q}\right) \cos(2\pi k\theta) \Bigg)^{j} d\theta - \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} \Bigg(\frac{1}{2} \sum_{k < \frac{q\log(q/H_n)}{H_n}} |a_k|^2 \Bigg)^{j/2} \right|^2 \nonumber \\ & \ll \left(\frac{Q}{4H_{n}(Q)} \right)^{j} e^{-2\log^{3/4}(Q/H_{n}(Q))}. \end{align} $$
Note that the coefficients
![]() $a_k$
here also depend on n, via the value of
$a_k$
here also depend on n, via the value of
![]() $q/H_{n}(q)$
.
$q/H_{n}(q)$
.
For if (6.2) holds, then the proportion of ‘bad’ primes
![]() $Q \leq q \leq 2Q$
for which
$Q \leq q \leq 2Q$
for which
 $$ \begin{align*} & \left(\frac{4H_{n}(q)}{q} \right)^{j} \\ & \left| \int_{0}^{1} \Bigg( \sum_{k < \frac{q\log(q/H_n)}{H_n}} a_k \left(\frac{k}{q}\right) \cos(2\pi k\theta) \Bigg)^{j} d\theta - \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} \Bigg(\frac{1}{2} \sum_{k < \frac{q\log(q/H_n)}{H_n}} |a_k|^2 \Bigg)^{j/2} \right|^2 \nonumber \\ & \gg e^{-0.1\log^{3/4}(Q/H_{n}(Q))} \nonumber \end{align*} $$
$$ \begin{align*} & \left(\frac{4H_{n}(q)}{q} \right)^{j} \\ & \left| \int_{0}^{1} \Bigg( \sum_{k < \frac{q\log(q/H_n)}{H_n}} a_k \left(\frac{k}{q}\right) \cos(2\pi k\theta) \Bigg)^{j} d\theta - \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} \Bigg(\frac{1}{2} \sum_{k < \frac{q\log(q/H_n)}{H_n}} |a_k|^2 \Bigg)^{j/2} \right|^2 \nonumber \\ & \gg e^{-0.1\log^{3/4}(Q/H_{n}(Q))} \nonumber \end{align*} $$
must be
![]() $\ll e^{-1.9\log ^{3/4}(Q/H_{n}(Q))}$
, and so the proportion for which this holds for some
$\ll e^{-1.9\log ^{3/4}(Q/H_{n}(Q))}$
, and so the proportion for which this holds for some
![]() $1 \leq j \leq \min \{\frac {\log ^{1/4}(Q/H_{n}(Q))}{50}, \frac {\log Q}{4\log (Q/H_{n}(Q))}\}$
must be
$1 \leq j \leq \min \{\frac {\log ^{1/4}(Q/H_{n}(Q))}{50}, \frac {\log Q}{4\log (Q/H_{n}(Q))}\}$
must be
Finally, the proportion of primes
![]() $Q \leq q \leq 2Q$
that are ‘bad’ for some n will be
$Q \leq q \leq 2Q$
that are ‘bad’ for some n will be
 $$ \begin{align*}\ll\kern-1pt \sum_{n} e^{-1.8\log^{3/4}(Q/H_{n}(Q))} = \kern-1pt\sum_{n} e^{-1.8 (1/\eta + n\eta)^{3/4}} \ll \kern-1pt\frac{1}{\eta^2} e^{-1.8 (1/\eta)^{3/4}} &\ll e^{- (1/\eta)^{3/4}} \\&= e^{- \min_{Q \leq q \leq 2Q}\log^{3/4}(q/H)} .\end{align*} $$
$$ \begin{align*}\ll\kern-1pt \sum_{n} e^{-1.8\log^{3/4}(Q/H_{n}(Q))} = \kern-1pt\sum_{n} e^{-1.8 (1/\eta + n\eta)^{3/4}} \ll \kern-1pt\frac{1}{\eta^2} e^{-1.8 (1/\eta)^{3/4}} &\ll e^{- (1/\eta)^{3/4}} \\&= e^{- \min_{Q \leq q \leq 2Q}\log^{3/4}(q/H)} .\end{align*} $$
So if we define our subsequence
![]() $\mathcal {P}_H$
of primes by discarding all the bad primes (in the above senseFootnote
4
) in each dyadic interval
$\mathcal {P}_H$
of primes by discarding all the bad primes (in the above senseFootnote
4
) in each dyadic interval
![]() $[Q,2Q]$
, then
$[Q,2Q]$
, then
![]() $\mathcal {P}_H$
has the density required in Theorem 3. And since the assumptions of Theorem 3 imply that
$\mathcal {P}_H$
has the density required in Theorem 3. And since the assumptions of Theorem 3 imply that
 $$ \begin{align*}\min\{\frac{\log^{1/4}(Q/H_{n}(Q))}{50}, \frac{\log Q}{4\log(Q/H_{n}(Q))}\} \gg \min_{Q \leq q \leq 2Q}\{\log^{1/4}(q/H(q)), \frac{\log q}{\log(q/H(q))}\} \rightarrow \infty\end{align*} $$
$$ \begin{align*}\min\{\frac{\log^{1/4}(Q/H_{n}(Q))}{50}, \frac{\log Q}{4\log(Q/H_{n}(Q))}\} \gg \min_{Q \leq q \leq 2Q}\{\log^{1/4}(q/H(q)), \frac{\log q}{\log(q/H(q))}\} \rightarrow \infty\end{align*} $$
as
![]() $Q \rightarrow \infty $
, the range of j for which the j-th moment of
$Q \rightarrow \infty $
, the range of j for which the j-th moment of
 $\Bigg ( \sum _{k < \frac {q\log (q/H_n)}{H_n}} a_k \left (\frac {k}{q}\right ) \cos (2\pi k\theta ) \Bigg )^{j}$
approaches the desired Gaussian moment will grow to infinity as
$\Bigg ( \sum _{k < \frac {q\log (q/H_n)}{H_n}} a_k \left (\frac {k}{q}\right ) \cos (2\pi k\theta ) \Bigg )^{j}$
approaches the desired Gaussian moment will grow to infinity as
![]() $q \rightarrow \infty $
with
$q \rightarrow \infty $
with
![]() $q \in \mathcal {P}_H$
.
$q \in \mathcal {P}_H$
.
6.4 The punchline
It now remains to establish (6.2). Recall that for the functions
![]() $H_{n}(q)$
from Section 6.3, the quantity
$H_{n}(q)$
from Section 6.3, the quantity
![]() $q/H_{n}(q)$
is constant (depending on n) for all
$q/H_{n}(q)$
is constant (depending on n) for all
![]() $Q \leq q \leq 2Q$
, and the coefficients
$Q \leq q \leq 2Q$
, and the coefficients
![]() $a_k = \frac {q \sin (\pi k H_{n}/q)}{\pi H_{n} k}$
depend only on k and n. Furthermore, by expanding the integral
$a_k = \frac {q \sin (\pi k H_{n}/q)}{\pi H_{n} k}$
depend only on k and n. Furthermore, by expanding the integral
 $$ \begin{align*} & \int_{0}^{1} \Bigg( \sum_{k < \frac{q\log(q/H_n)}{H_n}} a_k \left(\frac{k}{q}\right) \cos(2\pi k\theta) \Bigg)^{j} d\theta \\ &\quad = \sum_{m \leq (\frac{q\log(q/H_n)}{H_n})^j} \left(\frac{m}{q}\right) \sum_{\substack{k_1, \ldots, k_j < \frac{q\log(q/H_n)}{H_n}, \\ k_1 \cdot ... \cdot k_j = m}} \int_{0}^{1} \prod_{i=1}^{j} a_{k_i} \cos(2\pi k_{i} \theta) d\theta\end{align*} $$
$$ \begin{align*} & \int_{0}^{1} \Bigg( \sum_{k < \frac{q\log(q/H_n)}{H_n}} a_k \left(\frac{k}{q}\right) \cos(2\pi k\theta) \Bigg)^{j} d\theta \\ &\quad = \sum_{m \leq (\frac{q\log(q/H_n)}{H_n})^j} \left(\frac{m}{q}\right) \sum_{\substack{k_1, \ldots, k_j < \frac{q\log(q/H_n)}{H_n}, \\ k_1 \cdot ... \cdot k_j = m}} \int_{0}^{1} \prod_{i=1}^{j} a_{k_i} \cos(2\pi k_{i} \theta) d\theta\end{align*} $$
we see the left-hand side in (6.2) is of the form treated in Number Theory Result 3. (The subtracted term
![]() $\frac {j! \textbf {1}_{j \; \text {even}}}{(j/2)! 2^{j/2}} \left (\frac {1}{2} \sum _{k < \frac {q\log (q/H_n)}{H_n}} |a_k|^2 \right )^{j/2}$
in (6.2) may be thought of as part of the coefficient
$\frac {j! \textbf {1}_{j \; \text {even}}}{(j/2)! 2^{j/2}} \left (\frac {1}{2} \sum _{k < \frac {q\log (q/H_n)}{H_n}} |a_k|^2 \right )^{j/2}$
in (6.2) may be thought of as part of the coefficient
![]() $\alpha _1$
of the trivial Legendre symbol
$\alpha _1$
of the trivial Legendre symbol
![]() $\left (\frac {1}{q}\right )$
.) Note also that provided Q is large enough, we have
$\left (\frac {1}{q}\right )$
.) Note also that provided Q is large enough, we have
on the range of j required in (6.2). So we may apply Number Theory Result 3, and deduce (with a little manipulation of the error term) that
 $$ \begin{align*} & \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{prime}}} \\ &\left| \int_{0}^{1} \Bigg( \sum_{k < \frac{q\log(q/H_n)}{H_n}} a_k \left(\frac{k}{q}\right) \cos(2\pi k\theta) \Bigg)^{j} d\theta - \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} \Bigg(\frac{1}{2} \sum_{k < \frac{q\log(q/H_n)}{H_n}} |a_k|^2 \Bigg)^{j/2} \right|^2 \nonumber \\ & \ll \mathbb{E} \left| \int_{0}^{1} \Bigg( \sum_{k < \frac{q\log(q/H_n)}{H_n}} a_k f(k) \cos(2\pi k\theta) \Bigg)^{j} d\theta - \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} \Bigg(\frac{1}{2} \sum_{k < \frac{q\log(q/H_n)}{H_n}} |a_k|^2 \Bigg)^{j/2} \right|^2 \nonumber \\ & + \frac{Q^{0.26}}{Q^{0.99}} \Bigg( \Bigg( \sum_{k < \frac{q\log(q/H_n)}{H_n}} |a_k| \Bigg)^{j} + \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} \Bigg(\frac{1}{2} \sum_{k < \frac{q\log(q/H_n)}{H_n}} |a_k|^2 \Bigg)^{j/2} \Bigg)^2 , \nonumber \end{align*} $$
$$ \begin{align*} & \frac{\log Q}{Q} \sum_{\substack{Q \leq q \leq 2Q, \\ q \; \text{prime}}} \\ &\left| \int_{0}^{1} \Bigg( \sum_{k < \frac{q\log(q/H_n)}{H_n}} a_k \left(\frac{k}{q}\right) \cos(2\pi k\theta) \Bigg)^{j} d\theta - \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} \Bigg(\frac{1}{2} \sum_{k < \frac{q\log(q/H_n)}{H_n}} |a_k|^2 \Bigg)^{j/2} \right|^2 \nonumber \\ & \ll \mathbb{E} \left| \int_{0}^{1} \Bigg( \sum_{k < \frac{q\log(q/H_n)}{H_n}} a_k f(k) \cos(2\pi k\theta) \Bigg)^{j} d\theta - \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} \Bigg(\frac{1}{2} \sum_{k < \frac{q\log(q/H_n)}{H_n}} |a_k|^2 \Bigg)^{j/2} \right|^2 \nonumber \\ & + \frac{Q^{0.26}}{Q^{0.99}} \Bigg( \Bigg( \sum_{k < \frac{q\log(q/H_n)}{H_n}} |a_k| \Bigg)^{j} + \frac{j! \textbf{1}_{j \; \text{even}}}{(j/2)! 2^{j/2}} \Bigg(\frac{1}{2} \sum_{k < \frac{q\log(q/H_n)}{H_n}} |a_k|^2 \Bigg)^{j/2} \Bigg)^2 , \nonumber \end{align*} $$
where
![]() $f(k)$
is an extended Rademacher random multiplicative function. As we noted in Section 6.2, the
$f(k)$
is an extended Rademacher random multiplicative function. As we noted in Section 6.2, the
![]() $a_k$
are bounded in absolute value by 1, so the error term on the third line is
$a_k$
are bounded in absolute value by 1, so the error term on the third line is
![]() $\ll \frac {Q^{0.26}}{Q^{0.99}} \left ( (\frac {q\log (q/H_n)}{H_n})^j + j^{j/2} (\frac {q\log (q/H_n)}{H_n})^{j/2} \right )^2 \ll \frac {Q^{0.78}}{Q^{0.99}}$
, which is negligible.
$\ll \frac {Q^{0.26}}{Q^{0.99}} \left ( (\frac {q\log (q/H_n)}{H_n})^j + j^{j/2} (\frac {q\log (q/H_n)}{H_n})^{j/2} \right )^2 \ll \frac {Q^{0.78}}{Q^{0.99}}$
, which is negligible.
Finally, we apply the second part of Probability Result 2 to handle the expectation in the above display. Since the
![]() $a_k$
are real valued, bounded in absolute value by 1, and we only need to establish (6.2) for
$a_k$
are real valued, bounded in absolute value by 1, and we only need to establish (6.2) for
![]() $1 \leq j \leq \min \{\frac {\log ^{1/4}(Q/H_{n}(Q))}{50}, \frac {\log Q}{4\log (Q/H_{n}(Q))}\} \leq \frac {\log ^{1/4}(Q/H_{n}(Q))}{50}$
, we see all the conditions of Probability Result 2 are satisfied. Recall once more that
$1 \leq j \leq \min \{\frac {\log ^{1/4}(Q/H_{n}(Q))}{50}, \frac {\log Q}{4\log (Q/H_{n}(Q))}\} \leq \frac {\log ^{1/4}(Q/H_{n}(Q))}{50}$
, we see all the conditions of Probability Result 2 are satisfied. Recall once more that
![]() $q/H_{n}(q) = Q/H_{n}(Q)$
is constant for all
$q/H_{n}(q) = Q/H_{n}(Q)$
is constant for all
![]() $Q \leq q \leq 2Q$
. So our expectation is
$Q \leq q \leq 2Q$
. So our expectation is
 $$ \begin{align*} & \ll \left(\frac{Q}{H_{n}(Q)} \right)^{j - 1/15j} \log^{j}(Q/H_{n}(Q)) = \left(\frac{Q}{4 H_{n}(Q)} \right)^{j} e^{- \frac{\log(Q/H_{n}(Q))}{15j}} (4\log(Q/H_{n}(Q)))^j \nonumber \\ & \leq \left(\frac{Q}{4 H_{n}(Q)} \right)^{j} e^{- \frac{10\log^{3/4}(Q/H_{n}(Q))}{3}} (4\log(Q/H_{n}(Q)))^{\frac{\log^{1/4}(Q/H_{n}(Q))}{50}} , \nonumber \end{align*} $$
$$ \begin{align*} & \ll \left(\frac{Q}{H_{n}(Q)} \right)^{j - 1/15j} \log^{j}(Q/H_{n}(Q)) = \left(\frac{Q}{4 H_{n}(Q)} \right)^{j} e^{- \frac{\log(Q/H_{n}(Q))}{15j}} (4\log(Q/H_{n}(Q)))^j \nonumber \\ & \leq \left(\frac{Q}{4 H_{n}(Q)} \right)^{j} e^{- \frac{10\log^{3/4}(Q/H_{n}(Q))}{3}} (4\log(Q/H_{n}(Q)))^{\frac{\log^{1/4}(Q/H_{n}(Q))}{50}} , \nonumber \end{align*} $$
which is more than good enough to imply (6.2).
7 Proof of Theorem 4
The proof of Theorem 4 is very similar to, but simpler than, the proof of Theorem 3.
Recall the reductions from Section 6.1, and that our target distribution in Theorem 4 is
![]() $Z_1 + iZ_2$
with
$Z_1 + iZ_2$
with
![]() $Z_1, Z_2$
independent
$Z_1, Z_2$
independent
![]() $N(0,1/2)$
random variables, having moments
$N(0,1/2)$
random variables, having moments
![]() $\mathbb {E} (Z_1 + iZ_2)^j (\overline {Z_1 + iZ_2})^k = \frac {1}{\pi } \int _{-\infty }^{\infty } \int _{-\infty }^{\infty } (z_1 + iz_2)^j (z_1 - iz_2)^k e^{-z_1^2 - z_2^2} dz_1 dz_2 = k! \textbf {1}_{j=k}$
. (This is easy to check after rewriting the double integral in polar coordinates.) Then it will suffice to show the existence of sets
$\mathbb {E} (Z_1 + iZ_2)^j (\overline {Z_1 + iZ_2})^k = \frac {1}{\pi } \int _{-\infty }^{\infty } \int _{-\infty }^{\infty } (z_1 + iz_2)^j (z_1 - iz_2)^k e^{-z_1^2 - z_2^2} dz_1 dz_2 = k! \textbf {1}_{j=k}$
. (This is easy to check after rewriting the double integral in polar coordinates.) Then it will suffice to show the existence of sets
![]() $\mathcal {G}_{q,H}$
of characters mod q, with the sizes claimed in the theorem, such that for any choice of
$\mathcal {G}_{q,H}$
of characters mod q, with the sizes claimed in the theorem, such that for any choice of
![]() $\chi \in \mathcal {G}_{q,H}$
and all
$\chi \in \mathcal {G}_{q,H}$
and all
![]() $j, k \geq 0$
, we have
$j, k \geq 0$
, we have
 $$ \begin{align*} & \int_{0}^{1} \Bigg( \frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{1 \leq m < (q/H)\log(q/H)} \frac{\overline{\chi}(m) \sin(\pi m H/q)}{m} \cos(2\pi m\theta) \Bigg)^{j} \cdot \nonumber \\ & \cdot \Bigg( \overline{\frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{1 \leq m < (q/H)\log(q/H)} \frac{\overline{\chi}(m) \sin(\pi m H/q)}{m} \cos(2\pi m\theta)} \Bigg)^{k} d\theta \rightarrow k! \textbf{1}_{j=k} \quad \text{as } q \rightarrow \infty. \nonumber \end{align*} $$
$$ \begin{align*} & \int_{0}^{1} \Bigg( \frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{1 \leq m < (q/H)\log(q/H)} \frac{\overline{\chi}(m) \sin(\pi m H/q)}{m} \cos(2\pi m\theta) \Bigg)^{j} \cdot \nonumber \\ & \cdot \Bigg( \overline{\frac{2\sqrt{q}}{\pi \sqrt{H}} \sum_{1 \leq m < (q/H)\log(q/H)} \frac{\overline{\chi}(m) \sin(\pi m H/q)}{m} \cos(2\pi m\theta)} \Bigg)^{k} d\theta \rightarrow k! \textbf{1}_{j=k} \quad \text{as } q \rightarrow \infty. \nonumber \end{align*} $$
(As for Theorem 3, we actually need to show this with
![]() $\cos (2\pi m\theta )$
replaced by
$\cos (2\pi m\theta )$
replaced by
![]() $\sin (2\pi m\theta )$
as well, but that case will be exactly similar so we shall not discuss it further.)
$\sin (2\pi m\theta )$
as well, but that case will be exactly similar so we shall not discuss it further.)
If we set
![]() $a_m = a_{m,q,H} := \frac {q \sin (\pi m H/q)}{\pi H m}$
, as in Section 6.2, then we can rewrite our goal as being that for any choice of
$a_m = a_{m,q,H} := \frac {q \sin (\pi m H/q)}{\pi H m}$
, as in Section 6.2, then we can rewrite our goal as being that for any choice of
![]() $\chi \in \mathcal {G}_{q,H}$
and all
$\chi \in \mathcal {G}_{q,H}$
and all
![]() $j, k \geq 0$
, we have
$j, k \geq 0$
, we have
 $$ \begin{align*} & \left(\frac{4H}{q} \right)^{(j+k)/2} \\ &\quad \Bigg| \int_{0}^{1} \Bigg( \sum_{m < \frac{q \log(q/H)}{H} } a_m \overline{\chi}(m) \cos(2\pi m\theta) \Bigg)^{j} \Bigg( \overline{\sum_{m < \frac{q \log(q/H)}{H}} a_m \overline{\chi}(m) \cos(2\pi m\theta)} \Bigg)^{k} d\theta \nonumber \\ & \qquad- k! \textbf{1}_{j=k} \Bigg(\frac{1}{2} \sum_{m < \frac{q\log(q/H)}{H}} |a_m|^2 \Bigg)^{(j+k)/2} \Bigg| \rightarrow 0 \quad \text{as } q \rightarrow \infty. \nonumber \end{align*} $$
$$ \begin{align*} & \left(\frac{4H}{q} \right)^{(j+k)/2} \\ &\quad \Bigg| \int_{0}^{1} \Bigg( \sum_{m < \frac{q \log(q/H)}{H} } a_m \overline{\chi}(m) \cos(2\pi m\theta) \Bigg)^{j} \Bigg( \overline{\sum_{m < \frac{q \log(q/H)}{H}} a_m \overline{\chi}(m) \cos(2\pi m\theta)} \Bigg)^{k} d\theta \nonumber \\ & \qquad- k! \textbf{1}_{j=k} \Bigg(\frac{1}{2} \sum_{m < \frac{q\log(q/H)}{H}} |a_m|^2 \Bigg)^{(j+k)/2} \Bigg| \rightarrow 0 \quad \text{as } q \rightarrow \infty. \nonumber \end{align*} $$
To establish this, it will suffice to show that for all
![]() $0 \leq j, k \leq \min \{\frac {\log ^{1/4}(q/H(q))}{50}, \frac {\log q}{4\log (q/H(q))}\}$
, say, we have
$0 \leq j, k \leq \min \{\frac {\log ^{1/4}(q/H(q))}{50}, \frac {\log q}{4\log (q/H(q))}\}$
, say, we have
 $$ \begin{align} & \frac{1}{q-1} \sum_{\chi \; \text{mod} \; q} \Bigg| \int_{0}^{1} \Bigg( \sum_{m < \frac{q\log(q/H)}{H}} a_m \overline{\chi}(m) \cos(2\pi m\theta) \Bigg)^{j} \Bigg( \overline{\sum_{m < \frac{q\log(q/H)}{H}} a_m \overline{\chi}(m) \cos(2\pi m\theta)} \Bigg)^{k} d\theta \nonumber \\&\quad - k! \textbf{1}_{j=k} \Bigg(\frac{1}{2} \sum_{m < \frac{q\log(q/H)}{H}} |a_m|^2 \Bigg)^{(j+k)/2} \Bigg|^2 \ll \left(\frac{q}{4H} \right)^{j+k} e^{-2\log^{3/4}(q/H)}. \end{align} $$
$$ \begin{align} & \frac{1}{q-1} \sum_{\chi \; \text{mod} \; q} \Bigg| \int_{0}^{1} \Bigg( \sum_{m < \frac{q\log(q/H)}{H}} a_m \overline{\chi}(m) \cos(2\pi m\theta) \Bigg)^{j} \Bigg( \overline{\sum_{m < \frac{q\log(q/H)}{H}} a_m \overline{\chi}(m) \cos(2\pi m\theta)} \Bigg)^{k} d\theta \nonumber \\&\quad - k! \textbf{1}_{j=k} \Bigg(\frac{1}{2} \sum_{m < \frac{q\log(q/H)}{H}} |a_m|^2 \Bigg)^{(j+k)/2} \Bigg|^2 \ll \left(\frac{q}{4H} \right)^{j+k} e^{-2\log^{3/4}(q/H)}. \end{align} $$
For if we have (7.1), then the proportion of
![]() $\chi $
mod q for which
$\chi $
mod q for which
 $$ \begin{align*} & \left(\frac{4H}{q} \right)^{j+k} \Bigg| \int_{0}^{1} \Bigg( \sum_{m < (q/H)\log(q/H)} a_m \overline{\chi}(m) \cos(2\pi m\theta) \Bigg)^{j} \nonumber \\& \quad \times\Bigg( \overline{\sum_{m < (q/H)\log(q/H)} a_m \overline{\chi}(m) \cos(2\pi m\theta)} \Bigg)^{k} d\theta\\& \quad - k! \textbf{1}_{j=k} \Bigg(\frac{1}{2} \sum_{m < \frac{q\log(q/H)}{H}} |a_m|^2 \Bigg)^{(j+k)/2} \Bigg|^2 \gg e^{-0.1\log^{3/4}(q/H)} \nonumber \end{align*} $$
$$ \begin{align*} & \left(\frac{4H}{q} \right)^{j+k} \Bigg| \int_{0}^{1} \Bigg( \sum_{m < (q/H)\log(q/H)} a_m \overline{\chi}(m) \cos(2\pi m\theta) \Bigg)^{j} \nonumber \\& \quad \times\Bigg( \overline{\sum_{m < (q/H)\log(q/H)} a_m \overline{\chi}(m) \cos(2\pi m\theta)} \Bigg)^{k} d\theta\\& \quad - k! \textbf{1}_{j=k} \Bigg(\frac{1}{2} \sum_{m < \frac{q\log(q/H)}{H}} |a_m|^2 \Bigg)^{(j+k)/2} \Bigg|^2 \gg e^{-0.1\log^{3/4}(q/H)} \nonumber \end{align*} $$
must be
![]() $\ll e^{-1.9\log ^{3/4}(q/H)}$
, and so the proportion for which this holds for some pair of
$\ll e^{-1.9\log ^{3/4}(q/H)}$
, and so the proportion for which this holds for some pair of
![]() $0 \leq j, k \leq \min \{\frac {\log ^{1/4}(q/H)}{50}, \frac {\log q}{4\log (q/H)}\}$
must be
$0 \leq j, k \leq \min \{\frac {\log ^{1/4}(q/H)}{50}, \frac {\log q}{4\log (q/H)}\}$
must be
![]() $\ll \log ^{1/2}(q/H) e^{-1.9\log ^{3/4}(q/H)} \ll e^{-1.8\log ^{3/4}(q/H)}$
. Excluding any such characters mod q, our remaining set
$\ll \log ^{1/2}(q/H) e^{-1.9\log ^{3/4}(q/H)} \ll e^{-1.8\log ^{3/4}(q/H)}$
. Excluding any such characters mod q, our remaining set
![]() $\mathcal {G}_{q,H}$
of ‘good’ characters will satisfy
$\mathcal {G}_{q,H}$
of ‘good’ characters will satisfy
![]() $\#\mathcal {G}_{q,H} \geq q(1 - O(e^{-1.8\log ^{3/4}(q/H)}))$
, which is more than good enough for Theorem 4. And under the hypotheses of the theorem, we have
$\#\mathcal {G}_{q,H} \geq q(1 - O(e^{-1.8\log ^{3/4}(q/H)}))$
, which is more than good enough for Theorem 4. And under the hypotheses of the theorem, we have
![]() $e^{-0.1\log ^{3/4}(q/H)} \rightarrow 0$
as well as
$e^{-0.1\log ^{3/4}(q/H)} \rightarrow 0$
as well as
![]() $\min \{\frac {\log ^{1/4}(q/H(q))}{50}, \frac {\log q}{4\log (q/H(q))}\} \rightarrow \infty $
as
$\min \{\frac {\log ^{1/4}(q/H(q))}{50}, \frac {\log q}{4\log (q/H(q))}\} \rightarrow \infty $
as
![]() $q \rightarrow \infty $
, so for any fixed
$q \rightarrow \infty $
, so for any fixed
![]() $j,k$
and for
$j,k$
and for
![]() $\chi \in \mathcal {G}_{q,H}$
the moment will tend to the desired Gaussian moment.
$\chi \in \mathcal {G}_{q,H}$
the moment will tend to the desired Gaussian moment.
Now it only remains to verify (7.1). But expanding the square on the left-hand side there, using multiplicativity of
![]() $\chi $
and the condition that
$\chi $
and the condition that
![]() $j, k \leq \frac {\log q}{4\log (q/H)}$
, we see the resulting expression only involves
$j, k \leq \frac {\log q}{4\log (q/H)}$
, we see the resulting expression only involves
![]() $\chi $
and
$\chi $
and
![]() $\overline {\chi }$
applied to numbers that are
$\overline {\chi }$
applied to numbers that are
![]() $\leq ((q/H)\log (q/H))^{j+k} \leq q^{0.51}$
, say (for large enough q). Since this is
$\leq ((q/H)\log (q/H))^{j+k} \leq q^{0.51}$
, say (for large enough q). Since this is
![]() $< q$
, the orthogonality of Dirichlet characters implies that the left-hand side in (7.1) is exactly equal to
$< q$
, the orthogonality of Dirichlet characters implies that the left-hand side in (7.1) is exactly equal to
 $$ \begin{align*} & \mathbb{E} \Bigg| \int_{0}^{1} \Bigg( \sum_{m < \frac{q\log(q/H)}{H}} a_m f(m) \cos(2\pi m\theta) \Bigg)^{j} \Bigg( \overline{\sum_{m < \frac{q\log(q/H)}{H}} a_m f(m) \cos(2\pi m\theta)} \Bigg)^{k} d\theta \nonumber \\ &\quad - k! \textbf{1}_{j=k} \Bigg(\frac{1}{2} \sum_{m < \frac{q\log(q/H)}{H}} |a_m|^2 \Bigg)^{(j+k)/2} \Bigg|^2 , \nonumber \end{align*} $$
$$ \begin{align*} & \mathbb{E} \Bigg| \int_{0}^{1} \Bigg( \sum_{m < \frac{q\log(q/H)}{H}} a_m f(m) \cos(2\pi m\theta) \Bigg)^{j} \Bigg( \overline{\sum_{m < \frac{q\log(q/H)}{H}} a_m f(m) \cos(2\pi m\theta)} \Bigg)^{k} d\theta \nonumber \\ &\quad - k! \textbf{1}_{j=k} \Bigg(\frac{1}{2} \sum_{m < \frac{q\log(q/H)}{H}} |a_m|^2 \Bigg)^{(j+k)/2} \Bigg|^2 , \nonumber \end{align*} $$
where
![]() $f(m)$
is a Steinhaus random multiplicative function. The desired bound now follows immediately from Probability Result 3 and a small computation.
$f(m)$
is a Steinhaus random multiplicative function. The desired bound now follows immediately from Probability Result 3 and a small computation.
Acknowledgements
The author would like to thank K. Soundararajan and Max Xu for sharing a draft of their paper [Reference Soundararajan and Xu22], and Max Xu for some helpful comments. He would also like to thank the anonymous referee for their comments and suggestions.
Funding
Quite a lot of the research leading to this paper was carried out around 2016, when the author was supported by a research fellowship at Jesus College, Cambridge.
Competing interests
The author declares none.
Data availability statement
There is no data set associated with this paper.