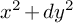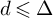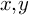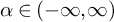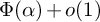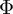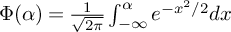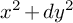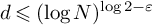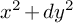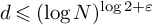1 Introduction
In this paper, we are interested in how many integers
![]() $\leq N$
are covered by the values taken by the quadratic forms
$\leq N$
are covered by the values taken by the quadratic forms
![]() $x^2 + dy^2$
,
$x^2 + dy^2$
,
![]() $d \leq \Delta $
. Our main result is the following, which gives a fairly complete answer to this question.
$d \leq \Delta $
. Our main result is the following, which gives a fairly complete answer to this question.
Theorem 1.1 (Main theorem)
Let N be large and write, for some real number
![]() $\alpha $
,
$\alpha $
,
Then
where
![]() $\Phi $
is the Gaussian distribution function
$\Phi $
is the Gaussian distribution function
![]() $\Phi (\alpha ) = \frac {1}{\sqrt {2\pi }} \int ^{\alpha }_{-\infty } e^{-x^2/2} dx$
.
$\Phi (\alpha ) = \frac {1}{\sqrt {2\pi }} \int ^{\alpha }_{-\infty } e^{-x^2/2} dx$
.
The problem of covering integers by this family of binary quadratic forms seems to have been first considered in the work of Hanson and Vaughan [Reference Hanson and Vaughan12]. Using the circle method, they established that almost all integers
![]() $n\leq N$
may be covered with
$n\leq N$
may be covered with
![]() $\Delta = \log N (\log \log N)^{3+\varepsilon }$
for any
$\Delta = \log N (\log \log N)^{3+\varepsilon }$
for any
![]() $\varepsilon>0$
and that a positive proportion of the integers below N may be covered using
$\varepsilon>0$
and that a positive proportion of the integers below N may be covered using
![]() $\Delta = \log N \log \log N$
. Diao [Reference Diao7] found a much shorter proof of the latter result, and in his argument d could be restricted to prime values so that a smaller set of forms is used.
$\Delta = \log N \log \log N$
. Diao [Reference Diao7] found a much shorter proof of the latter result, and in his argument d could be restricted to prime values so that a smaller set of forms is used.
Landau established that the number of integers below N that are sums of two squares is
![]() $\sim BN/(\log N)^{1/2}$
for a positive constant B. This was extended by Bernays to show that for any fixed primitive positive definite binary quadratic form f, the number of integers below N that are represented by f is
$\sim BN/(\log N)^{1/2}$
for a positive constant B. This was extended by Bernays to show that for any fixed primitive positive definite binary quadratic form f, the number of integers below N that are represented by f is
![]() $\sim B_f N (\log N)^{-1/2}$
, for a positive constant
$\sim B_f N (\log N)^{-1/2}$
, for a positive constant
![]() $B_f$
(which in fact depends only on the discriminant of f). More recently, Blomer [Reference Blomer1, Reference Blomer2] and Blomer and Granville [Reference Blomer and Granville3] consider in detail the number of integers up to N that are represented by f uniformly in the form f (thus allowing the discriminant to grow with N). These results, taken with the union bound, suggest that if
$B_f$
(which in fact depends only on the discriminant of f). More recently, Blomer [Reference Blomer1, Reference Blomer2] and Blomer and Granville [Reference Blomer and Granville3] consider in detail the number of integers up to N that are represented by f uniformly in the form f (thus allowing the discriminant to grow with N). These results, taken with the union bound, suggest that if
![]() $\Delta $
is smaller than
$\Delta $
is smaller than
![]() $(\log N)^{1/2-\varepsilon }$
, then almost all
$(\log N)^{1/2-\varepsilon }$
, then almost all
![]() $n\leq N$
cannot be covered by the forms
$n\leq N$
cannot be covered by the forms
![]() $x^2+dy^2$
with
$x^2+dy^2$
with
![]() $d\leq \Delta $
. However, as Theorem 1.1 reveals, the true threshold for
$d\leq \Delta $
. However, as Theorem 1.1 reveals, the true threshold for
![]() $\Delta $
is neither
$\Delta $
is neither
![]() $(\log N)^{1/2}$
nor
$(\log N)^{1/2}$
nor
![]() $\log N$
but instead
$\log N$
but instead
![]() $(\log N)^{\log 2}$
.
$(\log N)^{\log 2}$
.
We shall in fact prove a more precise version of Theorem 1.1, counting the number of integers below N with k prime factors that may be represented as
![]() $x^2+ dy^2$
with
$x^2+ dy^2$
with
![]() $d\leq \Delta $
. Throughout, let
$d\leq \Delta $
. Throughout, let
![]() $\Omega (n)$
denote the number of prime factors of n counted with multiplicity, and define
$\Omega (n)$
denote the number of prime factors of n counted with multiplicity, and define
Recall that most integers below N have about
![]() $\log \log N$
prime factors, a result first established by Hardy and Ramanujan. The well-known work of Erdős and Kac established that
$\log \log N$
prime factors, a result first established by Hardy and Ramanujan. The well-known work of Erdős and Kac established that
![]() $\Omega (n)$
has a normal distribution with mean
$\Omega (n)$
has a normal distribution with mean
![]() $\sim \log \log N$
and variance
$\sim \log \log N$
and variance
![]() $\sim \log \log N$
, while Selberg’s work [Reference Selberg16] gave still more precise results establishing an asymptotic formula for
$\sim \log \log N$
, while Selberg’s work [Reference Selberg16] gave still more precise results establishing an asymptotic formula for
![]() ${\mathcal A}(N,k)$
uniformly in a wide range of k. To reduce the visual complexity of expressions involving double logs later on, it is convenient to set (throughout the paper)
${\mathcal A}(N,k)$
uniformly in a wide range of k. To reduce the visual complexity of expressions involving double logs later on, it is convenient to set (throughout the paper)
The following simplified version of Selberg’s result is an immediate consequence of [Reference Tenenbaum17, Theorem II.6.5].
Lemma 1.2. Let N be large. Uniformly for integers k in the range
![]() $|k -k_0| \leq \tfrac 12 k_0$
, we have
$|k -k_0| \leq \tfrac 12 k_0$
, we have
 $$\begin{align*}|{\mathcal A}(N,k)| = \frac{N}{\log N} \frac{k_0^k}{k!}\Big( 1+ O\Big( \frac{1+|k-k_0|}{k_0}\Big)\Big). \end{align*}$$
$$\begin{align*}|{\mathcal A}(N,k)| = \frac{N}{\log N} \frac{k_0^k}{k!}\Big( 1+ O\Big( \frac{1+|k-k_0|}{k_0}\Big)\Big). \end{align*}$$
For a given k in a suitable interval around
![]() $\log \log N$
, we shall show (the ‘upper bound’, Theorem 1.3 below) that almost none of the integers in
$\log \log N$
, we shall show (the ‘upper bound’, Theorem 1.3 below) that almost none of the integers in
![]() ${\mathcal A}(N,k)$
are represented by
${\mathcal A}(N,k)$
are represented by
![]() $x^2+dy^2$
with
$x^2+dy^2$
with
![]() $d\leq \Delta $
if
$d\leq \Delta $
if
![]() $\Delta $
is a bit smaller than
$\Delta $
is a bit smaller than
![]() $2^k$
. This changes when
$2^k$
. This changes when
![]() $\Delta $
becomes a bit larger than
$\Delta $
becomes a bit larger than
![]() $2^k$
, when almost all the integers in
$2^k$
, when almost all the integers in
![]() ${\mathcal A}(N,k)$
may be so represented. This is the ‘lower bound’, Theorem 1.4 below. From these results, Theorem 1.1 will follow swiftly.
${\mathcal A}(N,k)$
may be so represented. This is the ‘lower bound’, Theorem 1.4 below. From these results, Theorem 1.1 will follow swiftly.
We turn now to the precise statements.
Theorem 1.3 (Upper bound)
Let N be large, and let k be an integer in the range
Suppose
![]() $\Delta \leq 2^k/k^4$
. The number of integers
$\Delta \leq 2^k/k^4$
. The number of integers
![]() $n \in {\mathcal A}(N,k)$
that may be written as
$n \in {\mathcal A}(N,k)$
that may be written as
![]() $x^2 + dy^2$
with
$x^2 + dy^2$
with
![]() $1\leq d\leq \Delta $
is
$1\leq d\leq \Delta $
is
![]() $\ll N/k_0$
.
$\ll N/k_0$
.
An application of Stirling’s formula (see (2.3) below) shows that for k in the range (1.1)
 $$ \begin{align*}|{\mathcal A}(N,k)| = \frac{N}{\sqrt{2\pi k_0}} \exp\Big( -\frac{(k-k_0)^2}{2k_0}\Big) \Big( 1+ O\Big( k_0^{-1/5}\Big) \Big). \end{align*} $$
$$ \begin{align*}|{\mathcal A}(N,k)| = \frac{N}{\sqrt{2\pi k_0}} \exp\Big( -\frac{(k-k_0)^2}{2k_0}\Big) \Big( 1+ O\Big( k_0^{-1/5}\Big) \Big). \end{align*} $$
Thus, Theorem 1.3 is really of interest only when
![]() $|k-k_0| \leq (k_0 \log k_0)^{1/2}$
. This range still includes most typical integers below N, and Theorem 1.3 may be used to establish the upper bound for the integers below N of the form
$|k-k_0| \leq (k_0 \log k_0)^{1/2}$
. This range still includes most typical integers below N, and Theorem 1.3 may be used to establish the upper bound for the integers below N of the form
![]() $x^2+dy^2$
with
$x^2+dy^2$
with
![]() $d\leq \Delta $
that is implicit in Theorem 1.1. The corresponding lower bound in Theorem 1.1 is implied by the following result.
$d\leq \Delta $
that is implicit in Theorem 1.1. The corresponding lower bound in Theorem 1.1 is implied by the following result.
Theorem 1.4 (Lower bound)
Let N be large, and let k be an integer in the range given in (1.1). Suppose
![]() $\Delta \geq k^3 2^k$
. Let
$\Delta \geq k^3 2^k$
. Let
![]() ${\mathcal E}(N,k)$
denote the set of integers in
${\mathcal E}(N,k)$
denote the set of integers in
![]() ${\mathcal A}(N,k)$
that cannot be represented as
${\mathcal A}(N,k)$
that cannot be represented as
![]() $x^2+dy^2$
with
$x^2+dy^2$
with
![]() $d\leq \Delta $
. Then
$d\leq \Delta $
. Then
Similarly to Theorem 1.3, Theorem 1.4 is really of interest only in the range
but this range includes most typical integers below N. In Section 2, we shall deduce our main result Theorem 1.1 from Theorems 1.3 and 1.4.
Since our main interest is in establishing Theorem 1.1, we have made no effort to optimize the error terms and ranges for k in Theorems 1.3 and 1.4. It would be of interest to establish analogues of these results uniformly in a wide range of k (although when k is large it may be better to work with
![]() $\omega (n)=k$
, where
$\omega (n)=k$
, where
![]() $\omega (n)$
counts the number of distinct prime factors of n). One case of particular interest may be
$\omega (n)$
counts the number of distinct prime factors of n). One case of particular interest may be
![]() $k=1$
: representing primes up to N using the quadratic forms
$k=1$
: representing primes up to N using the quadratic forms
![]() $x^2 +dy^2$
with
$x^2 +dy^2$
with
![]() $d\leq \Delta $
. Here, it would be possible to establish that a proportion
$d\leq \Delta $
. Here, it would be possible to establish that a proportion
![]() $\rho (\Delta )$
of the primes up to N may be so represented with
$\rho (\Delta )$
of the primes up to N may be so represented with
![]() $\rho (1)=1/2$
(by Fermat’s result on representing primes of the form
$\rho (1)=1/2$
(by Fermat’s result on representing primes of the form
![]() $1 \ (\operatorname {mod}\, 4)$
as a sum of two squares),
$1 \ (\operatorname {mod}\, 4)$
as a sum of two squares),
![]() $\rho (\Delta ) <1$
for all
$\rho (\Delta ) <1$
for all
![]() $\Delta $
, and
$\Delta $
, and
![]() $\rho (\Delta ) \to 1$
as
$\rho (\Delta ) \to 1$
as
![]() $\Delta \to \infty $
. Determining
$\Delta \to \infty $
. Determining
![]() $\rho (\Delta )$
precisely, or understanding its precise asymptotic behavior as
$\rho (\Delta )$
precisely, or understanding its precise asymptotic behavior as
![]() $\Delta $
gets large, seems like a challenging and delicate problem.
$\Delta $
gets large, seems like a challenging and delicate problem.
Let us indicate very briefly the ideas behind Theorems 1.3 and 1.4; here and in the rest of the introduction, we shall be a little informal and also assume that the reader is familiar with the classical theory of binary quadratic forms (which will be recalled in Section 3). Recall that a square-free integer n may be represented by some binary quadratic form of negative discriminant D if and only if
![]() $\chi _D(p)= 1$
for all primes p dividing n (assume that n is coprime to D). If n has k prime factors, then each condition
$\chi _D(p)= 1$
for all primes p dividing n (assume that n is coprime to D). If n has k prime factors, then each condition
![]() $\chi _D(p)=1$
has a
$\chi _D(p)=1$
has a
![]() $50\%$
chance of occurring so that n may be represented by some binary quadratic form of discriminant D with probability
$50\%$
chance of occurring so that n may be represented by some binary quadratic form of discriminant D with probability
![]() $2^{-k}$
. This suggests that
$2^{-k}$
. This suggests that
![]() $\Delta $
must be about size
$\Delta $
must be about size
![]() $2^k$
in order to have a chance of representing many integers with k prime factors. This is the idea behind Theorem 1.3, and it can be made precise without too much difficulty (see Section 4).
$2^k$
in order to have a chance of representing many integers with k prime factors. This is the idea behind Theorem 1.3, and it can be made precise without too much difficulty (see Section 4).
The more difficult part of our argument is Theorem 1.4, which constitutes the bulk of the paper. If
![]() $\Delta $
is substantially larger than
$\Delta $
is substantially larger than
![]() $2^k$
, then the heuristic that we just mentioned would suggest that for most integers
$2^k$
, then the heuristic that we just mentioned would suggest that for most integers
![]() $n\leq N$
with k prime factors there would be some negative discriminant D with
$n\leq N$
with k prime factors there would be some negative discriminant D with
![]() $|D|\leq \Delta $
such that n is representable by some binary quadratic form of discriminant D, and indeed, there would be a total of about
$|D|\leq \Delta $
such that n is representable by some binary quadratic form of discriminant D, and indeed, there would be a total of about
![]() $2^k$
such representations of n. The number of inequivalent classes of binary quadratic forms of discriminant D is the class number, which is of size
$2^k$
such representations of n. The number of inequivalent classes of binary quadratic forms of discriminant D is the class number, which is of size
![]() $|D|^{1/2+ o(1)}$
. It is therefore likely that some of the
$|D|^{1/2+ o(1)}$
. It is therefore likely that some of the
![]() $2^k$
(which is about
$2^k$
(which is about
![]() $\Delta $
) representations of n would come from the principal form
$\Delta $
) representations of n would come from the principal form
![]() $x^2+dy^2$
(corresponding to the discriminant
$x^2+dy^2$
(corresponding to the discriminant
![]() $D=-4d$
) and indeed that there should be about
$D=-4d$
) and indeed that there should be about
![]() $2^k/|D|^{1/2+o(1)}$
representations of n by
$2^k/|D|^{1/2+o(1)}$
representations of n by
![]() $x^2+dy^2$
. We make this heuristic precise by using class group characters and their associated L-functions, together with a second moment method. It would be relatively straightforward to obtain a version of Theorem 1.4 where a positive proportion of the elements in
$x^2+dy^2$
. We make this heuristic precise by using class group characters and their associated L-functions, together with a second moment method. It would be relatively straightforward to obtain a version of Theorem 1.4 where a positive proportion of the elements in
![]() ${\mathcal A}(N,k)$
are represented by the forms
${\mathcal A}(N,k)$
are represented by the forms
![]() $x^2+dy^2$
with
$x^2+dy^2$
with
![]() $d\leq \Delta $
. However, it is more delicate to obtain almost all integers in
$d\leq \Delta $
. However, it is more delicate to obtain almost all integers in
![]() ${\mathcal A}(N,k)$
, and to achieve this we impose congruence conditions on d for all primes p below a slowly growing parameter W. A key fact is that when discriminants d are restricted to such progressions, the value of
${\mathcal A}(N,k)$
, and to achieve this we impose congruence conditions on d for all primes p below a slowly growing parameter W. A key fact is that when discriminants d are restricted to such progressions, the value of
![]() $L(1,\chi _d)$
remains more or less constant. To simplify genus theory considerations, we further restrict attention to prime values of d, but this is merely a matter of convenience.
$L(1,\chi _d)$
remains more or less constant. To simplify genus theory considerations, we further restrict attention to prime values of d, but this is merely a matter of convenience.
For k sufficiently close to
![]() $k_0$
, Theorems 1.3 and 1.4 show that the number of represented elements in
$k_0$
, Theorems 1.3 and 1.4 show that the number of represented elements in
![]() ${\mathcal A}(N,k)$
undergoes a rapid phase transition as one goes from
${\mathcal A}(N,k)$
undergoes a rapid phase transition as one goes from
![]() $\Delta = 2^k/k^4$
(when
$\Delta = 2^k/k^4$
(when
![]() $0\%$
of
$0\%$
of
![]() ${\mathcal A}(N,k)$
is covered) to
${\mathcal A}(N,k)$
is covered) to
![]() $\Delta = 2^k k^3$
(when
$\Delta = 2^k k^3$
(when
![]() $100\%$
of
$100\%$
of
![]() ${\mathcal A}(N,k)$
is covered). While there is some scope to narrow the gap between
${\mathcal A}(N,k)$
is covered). While there is some scope to narrow the gap between
![]() $2^k/k^4$
and
$2^k/k^4$
and
![]() $2^k k^3$
, the restriction to prime values of d in our proof of Theorem 1.4 would prevent us from fully closing this gap. It seems likely that a more precise cutoff phenomenon occurs: When
$2^k k^3$
, the restriction to prime values of d in our proof of Theorem 1.4 would prevent us from fully closing this gap. It seems likely that a more precise cutoff phenomenon occurs: When
![]() $\Delta = \beta \sqrt {k} 2^k$
, there is a proportion
$\Delta = \beta \sqrt {k} 2^k$
, there is a proportion
![]() $p(\beta )$
of integers in
$p(\beta )$
of integers in
![]() ${\mathcal A}(N,k)$
that are represented, with
${\mathcal A}(N,k)$
that are represented, with
![]() $0< p(\beta ) <1$
for all
$0< p(\beta ) <1$
for all
![]() $0 < \beta < \infty $
, and with
$0 < \beta < \infty $
, and with
![]() $p(\beta ) \to 0$
as
$p(\beta ) \to 0$
as
![]() $\beta \to 0$
and
$\beta \to 0$
and
![]() $p(\beta ) \to 1$
as
$p(\beta ) \to 1$
as
![]() $\beta \to \infty $
. Possibly our arguments, together with additional ideas taking into account genus theory, could be used to establish part of this cutoff phenomenon, and we hope that an interested reader will take up the challenge.
$\beta \to \infty $
. Possibly our arguments, together with additional ideas taking into account genus theory, could be used to establish part of this cutoff phenomenon, and we hope that an interested reader will take up the challenge.
Our discussion so far has been confined to representing almost all integers below N using the forms
![]() $x^2+dy^2$
with
$x^2+dy^2$
with
![]() $d\leq \Delta $
. It is natural to ask what happens if all integers below N are to be represented. Taking
$d\leq \Delta $
. It is natural to ask what happens if all integers below N are to be represented. Taking
![]() $x= \lfloor \sqrt {n}\rfloor $
and
$x= \lfloor \sqrt {n}\rfloor $
and
![]() $y=1$
, we see that
$y=1$
, we see that
![]() $\Delta = 2\sqrt {N}$
suffices, and going beyond this trivial bound already seems an interesting problem. Since integers below N have
$\Delta = 2\sqrt {N}$
suffices, and going beyond this trivial bound already seems an interesting problem. Since integers below N have
![]() $\ll \log N/\log \log N$
distinct prime factors, extrapolating Theorem 1.4 we may expect that
$\ll \log N/\log \log N$
distinct prime factors, extrapolating Theorem 1.4 we may expect that
![]() $\Delta =\exp ( C \log N/\log \log N)$
is sufficient for some constant
$\Delta =\exp ( C \log N/\log \log N)$
is sufficient for some constant
![]() $C>0$
. As evidence towards this conjecture, we note that progress can be made in two weaker versions.
$C>0$
. As evidence towards this conjecture, we note that progress can be made in two weaker versions.
By a simple application of the pigeonhole principle, one can show that every positive integer below N may be represented by some nondegenerate binary quadratic form f with
![]() $|\text {disc}(f)| \leq \exp (C \log N/\log \log N)$
with C being any constant larger than
$|\text {disc}(f)| \leq \exp (C \log N/\log \log N)$
with C being any constant larger than
![]() $\log 4$
. Here, nondegenerate means that the quadratic form does not factor into linear forms or, equivalently, that the discriminant is not a square. In fact, all elements of
$\log 4$
. Here, nondegenerate means that the quadratic form does not factor into linear forms or, equivalently, that the discriminant is not a square. In fact, all elements of
![]() ${\mathcal A}(N,k)$
can be represented by some nondegenerate binary quadratic form with absolute discriminant
${\mathcal A}(N,k)$
can be represented by some nondegenerate binary quadratic form with absolute discriminant
![]() $\ll 4^k$
(for instance, all primes are of the form
$\ll 4^k$
(for instance, all primes are of the form
![]() $x^2+y^2$
,
$x^2+y^2$
,
![]() $x^2+ 2y^2$
or
$x^2+ 2y^2$
or
![]() $x^2-2y^2$
). The pigeonhole argument does not allow us to restrict attention to positive definite forms (although one can restrict attention to indefinite forms), let alone the smaller family of principal positive definite forms. Assuming GRH for quadratic Dirichlet L-functions it can be shown that all integers below N may be represented by some positive definite binary quadratic form with absolute discriminant below
$x^2-2y^2$
). The pigeonhole argument does not allow us to restrict attention to positive definite forms (although one can restrict attention to indefinite forms), let alone the smaller family of principal positive definite forms. Assuming GRH for quadratic Dirichlet L-functions it can be shown that all integers below N may be represented by some positive definite binary quadratic form with absolute discriminant below
![]() $\exp (C \log N/\log \log N)$
for any
$\exp (C \log N/\log \log N)$
for any
![]() $C> \log 4$
and indeed that all elements in
$C> \log 4$
and indeed that all elements in
![]() ${\mathcal A}(N,k)$
can be represented by such forms with absolute discriminant
${\mathcal A}(N,k)$
can be represented by such forms with absolute discriminant
![]() $\ll 4^k (\log N)^4$
.
$\ll 4^k (\log N)^4$
.
In the other direction, we may ask how large must
![]() $\Delta $
necessarily be if all integers
$\Delta $
necessarily be if all integers
![]() $n\leq N$
are represented as
$n\leq N$
are represented as
![]() $x^2 +dy^2$
with
$x^2 +dy^2$
with
![]() $d\leq \Delta $
. Complementing our discussion above, we can establish here that
$d\leq \Delta $
. Complementing our discussion above, we can establish here that
![]() $\Delta $
must be at least
$\Delta $
must be at least
![]() $\Delta _0= \exp (c \log N/\log \log N)$
for a positive constant c. In fact, we can establish the stronger result that there exists a square-free integer
$\Delta _0= \exp (c \log N/\log \log N)$
for a positive constant c. In fact, we can establish the stronger result that there exists a square-free integer
![]() $n\leq N$
such that for any fundamental discriminant d with
$n\leq N$
such that for any fundamental discriminant d with
![]() $1 < |d|\leq \Delta _0$
there exists a prime factor p of n with
$1 < |d|\leq \Delta _0$
there exists a prime factor p of n with
![]() $\chi _d(p)=-1$
. Such an integer n cannot be represented by any primitive nondegenerate binary quadratic form with absolute discriminant below
$\chi _d(p)=-1$
. Such an integer n cannot be represented by any primitive nondegenerate binary quadratic form with absolute discriminant below
![]() $\Delta _0$
. This result, which may be viewed as a variant of the least quadratic nonresidue problem, follows from an application of log-free zero density estimates; details will be supplied elsewhere.
$\Delta _0$
. This result, which may be viewed as a variant of the least quadratic nonresidue problem, follows from an application of log-free zero density estimates; details will be supplied elsewhere.
Lastly, we draw attention to three papers from the literature where related problems concerning the integers represented by a family of binary quadratic forms are considered: Blomer’s work on sums of two squareful numbers [Reference Blomer1], the work of Bourgain and Fuchs [Reference Bourgain and Fuchs4] on Apollonian circle packings and the work of Ghosh and Sarnak [Reference Ghosh and Sarnak10] on Markoff-type cubic surfaces.
Notation. For the most part notation will be introduced when it is needed. However, we remind the reader that
![]() $k_0$
will always denote
$k_0$
will always denote
![]() $\log \log N$
. From Section 5 onwards, W will denote a quantity which tends to infinity with N sufficiently slowly; we will take
$\log \log N$
. From Section 5 onwards, W will denote a quantity which tends to infinity with N sufficiently slowly; we will take
![]() $W := \log \log \log N$
for definiteness.
$W := \log \log \log N$
for definiteness.
Plan of the paper. Section 2 is devoted to the proof that the upper and lower bounds (Theorems 1.3 and 1.4, respectively) imply the main theorem, Theorem 1.1. Section 3 gives some standard background on binary quadratic forms which will be used throughout the rest of the paper. In Section 4, we prove the relatively straightforward upper bound, Theorem 1.3.
The remainder of the paper is devoted to the much more involved proof of the lower bound, Theorem 1.4. First, we formulate a more technical variant of this result, Theorem 5.1. This result allows us to restrict attention to representing integers not divisible by
![]() $4$
, using only quadratic forms
$4$
, using only quadratic forms
![]() $x^2 + dy^2$
with d ranging over primes in certain congruence classes. The deduction of Theorem 1.4 from Theorem 5.1 is short and is given immediately after the statement of the latter.
$x^2 + dy^2$
with d ranging over primes in certain congruence classes. The deduction of Theorem 1.4 from Theorem 5.1 is short and is given immediately after the statement of the latter.
The proof of Theorem 5.1 is via the second moment method. We divide the computations that arise into four separate technical propositions, Propositions 5.2, 5.3, 5.4 and 5.5. The synthesis of these propositions to give a proof of Theorem 5.1 is accomplished in Section 6.
The final sections of the main part of the paper are devoted to the proofs of these four technical propositions. Proposition 5.5 is a statement about averages of certain
![]() $L(1,\chi )$
, and we handle it first, in Section 7. The remaining three results all require some background on class group L-functions, and Section 8 provides an overview and references for the necessary material. Finally, the proofs of Propositions 5.2, 5.3 and 5.4 are given in Sections 9, 10 and 11, respectively.
$L(1,\chi )$
, and we handle it first, in Section 7. The remaining three results all require some background on class group L-functions, and Section 8 provides an overview and references for the necessary material. Finally, the proofs of Propositions 5.2, 5.3 and 5.4 are given in Sections 9, 10 and 11, respectively.
Sections 8, 9 and 10 use Selberg’s techniques [Reference Selberg16]. There is no particularly convenient reference for what we require, so we provide full details. The more standard parts of this may be found in Appendix A.
2 The upper and lower bounds imply the main theorem
In this section, we show how Theorem 1.1 follows from Theorems 1.3 and 1.4.
Suppose, as in the statement of Theorem 1.1, that
![]() $\Delta = (\log N)^{\log 2} 2^{\alpha \sqrt {\log \log N}}$
. It is enough to prove the result for
$\Delta = (\log N)^{\log 2} 2^{\alpha \sqrt {\log \log N}}$
. It is enough to prove the result for
the result for all
![]() $\alpha $
follows from this case and the fact that
$\alpha $
follows from this case and the fact that
Suppose henceforth that (2.1) holds.
Let
![]() $k^-$
be defined as the solution to
$k^-$
be defined as the solution to
![]() $\Delta = k^3 2^k$
and
$\Delta = k^3 2^k$
and
![]() $k^+$
as the solution to
$k^+$
as the solution to
![]() $\Delta = 2^k/k^4$
. Then, one may check that
$\Delta = 2^k/k^4$
. Then, one may check that
In particular, by the assumption (2.1), we see that
![]() $|k^{\pm } - k_0| \leq 2 k_0^{3/5}$
.
$|k^{\pm } - k_0| \leq 2 k_0^{3/5}$
.
For k in the range
![]() $k_0-2 k_0^{3/5} \leq k \leq k^-$
, Theorem 1.4 shows that the number of integers in
$k_0-2 k_0^{3/5} \leq k \leq k^-$
, Theorem 1.4 shows that the number of integers in
![]() ${\mathcal A}(N,k)$
that may be represented as
${\mathcal A}(N,k)$
that may be represented as
![]() $x^2+dy^2$
with
$x^2+dy^2$
with
![]() $d\leq \Delta $
is
$d\leq \Delta $
is
Stirling’s formula and the approximation
![]() $1 -x = \exp (-x -\frac {x^2}{2} + O(x^3))$
with
$1 -x = \exp (-x -\frac {x^2}{2} + O(x^3))$
with
![]() $x = 1 - \frac {k_0}{k}$
(
$x = 1 - \frac {k_0}{k}$
(
![]() $ = O(k_0^{-2/5})$
) show in this range of k that
$ = O(k_0^{-2/5})$
) show in this range of k that
 $$ \begin{align} \frac{k_0^k}{k!} = \frac{1}{\sqrt{2\pi k_0}} \exp\Big( k_0 - \frac{(k_0-k)^2}{2k_0} + O\big( k_0^{-1/5}\big) \Big) \end{align} $$
$$ \begin{align} \frac{k_0^k}{k!} = \frac{1}{\sqrt{2\pi k_0}} \exp\Big( k_0 - \frac{(k_0-k)^2}{2k_0} + O\big( k_0^{-1/5}\big) \Big) \end{align} $$
so that using Lemma 1.2, we may see that the quantity in (2.2) is
 $$ \begin{align*}\frac{N}{\sqrt{2\pi k_0} } \exp\Big( -\frac{(k-k_0)^2}{2k_0}\Big) \Big(1 + O\Big( \frac{1}{\log k_0} \Big) \Big) + O\big(N k_0^{-3/4}\big). \end{align*} $$
$$ \begin{align*}\frac{N}{\sqrt{2\pi k_0} } \exp\Big( -\frac{(k-k_0)^2}{2k_0}\Big) \Big(1 + O\Big( \frac{1}{\log k_0} \Big) \Big) + O\big(N k_0^{-3/4}\big). \end{align*} $$
Summing over all k in this range, we conclude that the number of integers
![]() $n\leq N$
that may be written as
$n\leq N$
that may be written as
![]() $x^2+dy^2$
with
$x^2+dy^2$
with
![]() $d\leq \Delta $
is at least
$d\leq \Delta $
is at least
 $$ \begin{align*}\frac{N}{\sqrt{2\pi k_0}} \sum_{k_0 - 2k_0^{3/5} \leq k \leq k^- } \exp\Big( - \frac{(k-k_0)^2}{2k_0}\Big) + O\Big(\frac{N}{\log k_0} \Big) = (\Phi(\alpha) +o(1)) N, \end{align*} $$
$$ \begin{align*}\frac{N}{\sqrt{2\pi k_0}} \sum_{k_0 - 2k_0^{3/5} \leq k \leq k^- } \exp\Big( - \frac{(k-k_0)^2}{2k_0}\Big) + O\Big(\frac{N}{\log k_0} \Big) = (\Phi(\alpha) +o(1)) N, \end{align*} $$
upon approximating the sum by the corresponding integral. This shows the lower bound implicit in Theorem 1.1.
To obtain the corresponding upper bound, note that for k in the range
![]() $k^+ \leq k \leq k_0+2k_0^{3/5}$
, Theorem 1.3 shows that the number of integers in
$k^+ \leq k \leq k_0+2k_0^{3/5}$
, Theorem 1.3 shows that the number of integers in
![]() ${\mathcal A}(N,k)$
that cannot be represented as
${\mathcal A}(N,k)$
that cannot be represented as
![]() $x^2+dy^2$
with
$x^2+dy^2$
with
![]() $d\leq \Delta $
is
$d\leq \Delta $
is
![]() $|{\mathcal A}(N,k)| + O(N/k_0)$
. Using Lemma 1.2 and Stirling’s formula as above, this is
$|{\mathcal A}(N,k)| + O(N/k_0)$
. Using Lemma 1.2 and Stirling’s formula as above, this is
 $$ \begin{align*}\frac{N}{\sqrt{2\pi k_0} } \exp\Big( -\frac{(k-k_0)^2}{2k_0}\Big) \Big(1 + O\big( k_0^{-1/5} \big) \Big) + O\big(Nk_0^{-1}\big). \end{align*} $$
$$ \begin{align*}\frac{N}{\sqrt{2\pi k_0} } \exp\Big( -\frac{(k-k_0)^2}{2k_0}\Big) \Big(1 + O\big( k_0^{-1/5} \big) \Big) + O\big(Nk_0^{-1}\big). \end{align*} $$
Summing over all k in this range, we conclude the number of integers up to N that cannot be represented as
![]() $x^2+dy^2$
with
$x^2+dy^2$
with
![]() $d\leq \Delta $
is at least
$d\leq \Delta $
is at least
 $$ \begin{align*}\frac{N}{\sqrt{2\pi k_0}} \sum_{k^+ \leq k \leq k_0 +2k_0^{3/5} } \exp\Big( - \frac{(k-k_0)^2}{2k_0}\Big) + O\big(N k_0^{-1/5} \big) = (1-\Phi(\alpha) +o(1)) N. \end{align*} $$
$$ \begin{align*}\frac{N}{\sqrt{2\pi k_0}} \sum_{k^+ \leq k \leq k_0 +2k_0^{3/5} } \exp\Big( - \frac{(k-k_0)^2}{2k_0}\Big) + O\big(N k_0^{-1/5} \big) = (1-\Phi(\alpha) +o(1)) N. \end{align*} $$
This implies the upper bound implicit in Theorem 1.1 and completes the proof.
3 Background on quadratic forms
For the theory in the rest of this section, good resources are [Reference Cox5], [Reference Davenport6], [Reference Iwaniec and Kowalski13, Chapter 22] or [Reference Zagier19].
3.1 Fundamental discriminants and characters
A fundamental discriminant is an integer D of the following type: either (i)
![]() $D \equiv 1 \ (\operatorname {mod}\, 4)$
and square-free or (ii)
$D \equiv 1 \ (\operatorname {mod}\, 4)$
and square-free or (ii)
![]() $D = 4m$
with
$D = 4m$
with
![]() $m \equiv 2,3 \ (\operatorname {mod}\, 4)$
and m square-free. Apart from
$m \equiv 2,3 \ (\operatorname {mod}\, 4)$
and m square-free. Apart from
![]() $D = 1$
, these are precisely the discriminants of quadratic fields over
$D = 1$
, these are precisely the discriminants of quadratic fields over
![]() $\mathbf {Q}$
, and indeed the discriminant of
$\mathbf {Q}$
, and indeed the discriminant of
![]() $\mathbf {Q}(\sqrt {D})$
is D. Equivalently, if m is square-free, the quadratic field
$\mathbf {Q}(\sqrt {D})$
is D. Equivalently, if m is square-free, the quadratic field
![]() $\mathbf {Q}(\sqrt {m})$
has discriminant
$\mathbf {Q}(\sqrt {m})$
has discriminant
![]() $4m$
if
$4m$
if
![]() $m \equiv 2,3 \ (\operatorname {mod}\, 4)$
and m if
$m \equiv 2,3 \ (\operatorname {mod}\, 4)$
and m if
![]() $m \equiv 1\ (\operatorname {mod}\, 4)$
.
$m \equiv 1\ (\operatorname {mod}\, 4)$
.
Associated to the fundamental discriminant D is the primitive quadratic Dirichlet character
![]() $\chi _{D}(n) = (\frac {D}{n})$
, where the symbol here is the Kronecker symbol. This is defined to be completely multiplicative and specified on the primes by the following:
$\chi _{D}(n) = (\frac {D}{n})$
, where the symbol here is the Kronecker symbol. This is defined to be completely multiplicative and specified on the primes by the following:
-
• If p is an odd prime,
 $\chi _{D}(p)= (\frac {D}{p})$
is the Legendre symbol;
$\chi _{D}(p)= (\frac {D}{p})$
is the Legendre symbol; -
•
 $\chi _{D}(2) = 0$
if
$\chi _{D}(2) = 0$
if
 $D \equiv 0 \ (\operatorname {mod}\, 4)$
,
$D \equiv 0 \ (\operatorname {mod}\, 4)$
,
 $1$
if
$1$
if
 $D \equiv 1 \ (\operatorname {mod}\, 8)$
and
$D \equiv 1 \ (\operatorname {mod}\, 8)$
and
 $-1$
if
$-1$
if
 $D \equiv 5\ (\operatorname {mod}\, 8)$
;
$D \equiv 5\ (\operatorname {mod}\, 8)$
; -
•
 $\chi _{D}(-1) = \mbox {sgn}(D)$
.
$\chi _{D}(-1) = \mbox {sgn}(D)$
.
The Kronecker symbol
![]() $\chi _{D}$
is a primitive character of modulus
$\chi _{D}$
is a primitive character of modulus
![]() $|D|$
. It describes the splitting type of a prime p in the quadratic field
$|D|$
. It describes the splitting type of a prime p in the quadratic field
![]() $K=\mathbf {Q}(\sqrt {D})$
: A prime p splits in
$K=\mathbf {Q}(\sqrt {D})$
: A prime p splits in
![]() $\mathbf {Q}(\sqrt {D})$
if
$\mathbf {Q}(\sqrt {D})$
if
![]() $(\frac {D}{p})=1$
, remains inert if
$(\frac {D}{p})=1$
, remains inert if
![]() $(\frac {D}{p}) =-1$
and ramifies when
$(\frac {D}{p}) =-1$
and ramifies when
![]() $(\frac {D}{p})=0$
. Thus, the Dedekind zeta-function of the field K is given by
$(\frac {D}{p})=0$
. Thus, the Dedekind zeta-function of the field K is given by
and the number of ideals in
![]() $\mathcal {O}_K$
of norm n is
$\mathcal {O}_K$
of norm n is
 $$ \begin{align*}(1 \ast \chi_{D})(n) = \sum_{\ell | n} \chi_{D}(\ell). \end{align*} $$
$$ \begin{align*}(1 \ast \chi_{D})(n) = \sum_{\ell | n} \chi_{D}(\ell). \end{align*} $$
3.2 Positive definite forms and imaginary quadratic fields
Let
![]() $D < 0$
be a negative fundamental discriminant, and let
$D < 0$
be a negative fundamental discriminant, and let
![]() $K= \mathbf {Q}(\sqrt {D})$
denote the corresponding imaginary quadratic field.
$K= \mathbf {Q}(\sqrt {D})$
denote the corresponding imaginary quadratic field.
There is a well-known correspondence (going back to Gauss) between ideal classes in K and equivalence classes of positive definite binary quadratic forms of discriminant D. In particular, principal ideals in K are in correspondence with the principal binary quadratic form given by
![]() $x^2 + \frac {|D|}4 y^2$
(in the case
$x^2 + \frac {|D|}4 y^2$
(in the case
![]() $D\equiv 0 \ (\operatorname {mod}\, 4)$
) and
$D\equiv 0 \ (\operatorname {mod}\, 4)$
) and
![]() $x^2 + xy + \frac {1+|D|}{4} y^2$
(in the case
$x^2 + xy + \frac {1+|D|}{4} y^2$
(in the case
![]() $D \equiv 1 \ (\operatorname {mod}\, 4)$
so that
$D \equiv 1 \ (\operatorname {mod}\, 4)$
so that
![]() $|D|=-D \equiv 3 \ (\operatorname {mod}\, 4)$
).
$|D|=-D \equiv 3 \ (\operatorname {mod}\, 4)$
).
A key object of interest for us is
which counts the number of principal ideals in
![]() ${\mathcal O}_K$
of norm n. If
${\mathcal O}_K$
of norm n. If
![]() $D\equiv 0 \ (\operatorname {mod}\, 4)$
, then a principal ideal
$D\equiv 0 \ (\operatorname {mod}\, 4)$
, then a principal ideal
![]() ${\mathfrak a}$
of norm n may be written as
${\mathfrak a}$
of norm n may be written as
![]() $(a+b\sqrt {D/4})$
and corresponds to two representations of n by the principal form
$(a+b\sqrt {D/4})$
and corresponds to two representations of n by the principal form
![]() $x^2+ \frac {|D|}{4} y^2$
, namely
$x^2+ \frac {|D|}{4} y^2$
, namely
![]() $n= (\pm a)^2 + \frac {|D|}{4} (\pm b)^2$
(with the exception of
$n= (\pm a)^2 + \frac {|D|}{4} (\pm b)^2$
(with the exception of
![]() $D=-4$
, where it corresponds to
$D=-4$
, where it corresponds to
![]() $4$
representations by the principal form
$4$
representations by the principal form
![]() $x^2+y^2$
). Similarly, if
$x^2+y^2$
). Similarly, if
![]() $D\equiv 1\ (\operatorname {mod}\, 4)$
, a principal ideal
$D\equiv 1\ (\operatorname {mod}\, 4)$
, a principal ideal
![]() ${\mathfrak a}$
of norm n may be written as
${\mathfrak a}$
of norm n may be written as
![]() $(a + b \frac {1+\sqrt {D}}{2})$
and corresponds to two representations of n by the principal form
$(a + b \frac {1+\sqrt {D}}{2})$
and corresponds to two representations of n by the principal form
![]() $x^2 +xy + \frac {1+|D|}{4} y^2$
(with the exception of
$x^2 +xy + \frac {1+|D|}{4} y^2$
(with the exception of
![]() $D=-3$
, where it corresponds to
$D=-3$
, where it corresponds to
![]() $6$
representations by the principal form
$6$
representations by the principal form
![]() $x^2+xy+y^2$
).
$x^2+xy+y^2$
).
We remark that
since
![]() $(1*\chi _D)(n)$
counts all ideals with norm n, and that each ideal of norm n corresponds to two (or
$(1*\chi _D)(n)$
counts all ideals with norm n, and that each ideal of norm n corresponds to two (or
![]() $4$
when
$4$
when
![]() $D=-4$
, or
$D=-4$
, or
![]() $6$
when
$6$
when
![]() $D=-3$
) representations of n by some equivalence class of binary quadratic forms of discriminant D.
$D=-3$
) representations of n by some equivalence class of binary quadratic forms of discriminant D.
To isolate the principal ideals of norm n, we shall use class group characters. Let
![]() $C_K$
denote the ideal class group of K, and denote by
$C_K$
denote the ideal class group of K, and denote by
![]() $h_K$
its size which is the class number of K. A class group character is a homomorphism
$h_K$
its size which is the class number of K. A class group character is a homomorphism
![]() $\psi : C_K \to \mathbf {C}^{\times }$
. We may think of such class group characters as maps
$\psi : C_K \to \mathbf {C}^{\times }$
. We may think of such class group characters as maps
satisfying
![]() $\psi ({\mathfrak a }{\mathfrak b}) = \psi ({\mathfrak a}) \psi ({\mathfrak b})$
and
$\psi ({\mathfrak a }{\mathfrak b}) = \psi ({\mathfrak a}) \psi ({\mathfrak b})$
and
![]() $\psi ((\lambda )) = 1$
for every nonzero principal ideal
$\psi ((\lambda )) = 1$
for every nonzero principal ideal
![]() $(\lambda )$
. We denote the dual group of class group characters by
$(\lambda )$
. We denote the dual group of class group characters by
![]() ${\widehat C}_K$
.
${\widehat C}_K$
.
If
![]() $\psi \in {\widehat C}_K$
is a class group character, then we define
$\psi \in {\widehat C}_K$
is a class group character, then we define
 $$ \begin{align} r(n,\psi) = r(n,\psi; D) = \sum_{N(\mathfrak a)=n} \psi({\mathfrak a}). \end{align} $$
$$ \begin{align} r(n,\psi) = r(n,\psi; D) = \sum_{N(\mathfrak a)=n} \psi({\mathfrak a}). \end{align} $$
Notice that
![]() ${\widehat C}_K$
always includes the principal character
${\widehat C}_K$
always includes the principal character
![]() $\psi _0$
given by
$\psi _0$
given by
![]() $\psi _0(\mathfrak a) =1$
for all ideals
$\psi _0(\mathfrak a) =1$
for all ideals
![]() ${\mathfrak a}$
. In this case,
${\mathfrak a}$
. In this case,
 $$ \begin{align} r(n,\psi_0) = \sum_{N(\mathfrak a)=n} 1 = (1*\chi_D)(n). \end{align} $$
$$ \begin{align} r(n,\psi_0) = \sum_{N(\mathfrak a)=n} 1 = (1*\chi_D)(n). \end{align} $$
The orthogonality relations for characters now allow us to express
![]() $R_D(n)$
in terms of
$R_D(n)$
in terms of
![]() $r(n,\psi )$
: namely,
$r(n,\psi )$
: namely,
 $$ \begin{align} R_D(n) = \frac{1}{h_K} \sum_{\psi \in {\widehat C}_K} r(n, \psi). \end{align} $$
$$ \begin{align} R_D(n) = \frac{1}{h_K} \sum_{\psi \in {\widehat C}_K} r(n, \psi). \end{align} $$
With these preliminaries in place, we postpone a more detailed discussion of class group characters to Section 8.
3.3 Representation by
 $x^2+dy^2$
$x^2+dy^2$
We now relate the concepts of the previous section to our specific problem of representing integers by the quadratic forms
![]() $x^2+dy^2$
. We will restrict attention to square-free integers d, which is sufficient for our purposes. The problem of representing integers by
$x^2+dy^2$
. We will restrict attention to square-free integers d, which is sufficient for our purposes. The problem of representing integers by
![]() $x^2+dy^2$
is naturally related to arithmetic in the field
$x^2+dy^2$
is naturally related to arithmetic in the field
![]() $K=\mathbf {Q}(\sqrt {-d}) = \mathbf {Q}(\sqrt {D})$
, where D denotes the fundamental discriminant
$K=\mathbf {Q}(\sqrt {-d}) = \mathbf {Q}(\sqrt {D})$
, where D denotes the fundamental discriminant
 $$ \begin{align} D = \begin{cases} -4d &\text{ if } d \equiv 1,2 \ (\operatorname{mod}\, 4), \\ -d & \text{ if } d \equiv 3\ (\operatorname{mod}\, 4). \end{cases} \end{align} $$
$$ \begin{align} D = \begin{cases} -4d &\text{ if } d \equiv 1,2 \ (\operatorname{mod}\, 4), \\ -d & \text{ if } d \equiv 3\ (\operatorname{mod}\, 4). \end{cases} \end{align} $$
Henceforth in the paper, we will adopt the following notational conventions. Unless explicitly stated otherwise, whenever we write d we have in mind a square-free integer, and corresponding to such d will be the fundamental discriminant D given in (3.5), and the imaginary quadratic field
![]() $K = \mathbf {Q}(\sqrt {-d}) = \mathbf {Q}(\sqrt {D})$
. Of course, K and D depend on d, but we will not indicate this explicitly. Sometimes, we will additionally have a second positive square-free number
$K = \mathbf {Q}(\sqrt {-d}) = \mathbf {Q}(\sqrt {D})$
. Of course, K and D depend on d, but we will not indicate this explicitly. Sometimes, we will additionally have a second positive square-free number
![]() $d'$
, and
$d'$
, and
![]() $K', D'$
will be associated to it in the same way.
$K', D'$
will be associated to it in the same way.
Lemma 3.1. Let
![]() $d \ge 1$
be square-free, and let
$d \ge 1$
be square-free, and let
![]() $D, K$
be associated to d as above.
$D, K$
be associated to d as above.
-
1. If
 $d \equiv 1$
or
$d \equiv 1$
or
 $2 \ (\operatorname {mod}\, 4)$
, then the number of representations of n by the quadratic form
$2 \ (\operatorname {mod}\, 4)$
, then the number of representations of n by the quadratic form
 $x^2 + dy^2$
equals
$x^2 + dy^2$
equals
 $2R_D(n)$
, with the exception of the special case
$2R_D(n)$
, with the exception of the special case
 $d=1$
where it equals
$d=1$
where it equals
 $4 R_{-4}(n)$
.
$4 R_{-4}(n)$
. -
2. If
 $d\equiv 3\ (\operatorname {mod}\, 4)$
, then the number of representations of n by the quadratic form
$d\equiv 3\ (\operatorname {mod}\, 4)$
, then the number of representations of n by the quadratic form
 $x^2+dy^2$
is at most
$x^2+dy^2$
is at most
 $2 R_D(n)$
, with the exception of the special case
$2 R_D(n)$
, with the exception of the special case
 $d=3$
where it is at most
$d=3$
where it is at most
 $6R_{-3}(n)$
.
$6R_{-3}(n)$
. -
3. If
 $d \equiv 7 \ (\operatorname {mod}\, 8)$
and n is odd, then the number of representations of n by the quadratic form
$d \equiv 7 \ (\operatorname {mod}\, 8)$
and n is odd, then the number of representations of n by the quadratic form
 $x^2+dy^2$
equals
$x^2+dy^2$
equals
 $2R_D(n)$
.
$2R_D(n)$
.
Proof. If
![]() $d\equiv 1, 2 \ (\operatorname {mod}\, 4)$
, we have
$d\equiv 1, 2 \ (\operatorname {mod}\, 4)$
, we have
![]() $D= -4d$
, and the quadratic form
$D= -4d$
, and the quadratic form
![]() $x^2 +dy^2$
is the principal form of discriminant D. The result (1) now follows from our discussion in Section 3.2.
$x^2 +dy^2$
is the principal form of discriminant D. The result (1) now follows from our discussion in Section 3.2.
If
![]() $d\equiv 3 \ (\operatorname {mod}\, 4)$
, then
$d\equiv 3 \ (\operatorname {mod}\, 4)$
, then
![]() $D=-d$
, and the principal form of discriminant D is
$D=-d$
, and the principal form of discriminant D is
![]() $x^2+xy + \frac {1+d}{4} y^2$
. The identity
$x^2+xy + \frac {1+d}{4} y^2$
. The identity
shows that the representations of n as
![]() $x^2+dy^2$
are in bijective correspondence with the representations of n as
$x^2+dy^2$
are in bijective correspondence with the representations of n as
![]() $X^2 + XY + \frac {1+d}{4} Y^2$
with Y even. Since the total number of representations of n as
$X^2 + XY + \frac {1+d}{4} Y^2$
with Y even. Since the total number of representations of n as
![]() $X^2+XY +\frac {1+d}{4} Y^2$
(ignoring whether Y is even or odd) equals
$X^2+XY +\frac {1+d}{4} Y^2$
(ignoring whether Y is even or odd) equals
![]() $2R_D(n)$
(or
$2R_D(n)$
(or
![]() $6R_{-3}(n)$
in the exceptional case
$6R_{-3}(n)$
in the exceptional case
![]() $d=-3$
), the upper bound stated in (2) follows.
$d=-3$
), the upper bound stated in (2) follows.
Finally, if
![]() $d\equiv 7 \ (\operatorname {mod}\, 8)$
and n is odd, then
$d\equiv 7 \ (\operatorname {mod}\, 8)$
and n is odd, then
![]() $\frac {1+d}{4}$
is even, and so any representation of n as
$\frac {1+d}{4}$
is even, and so any representation of n as
![]() $X^2+XY+ \frac {1+d}{4} Y^2$
must necessarily have Y being even. Thus, in this case the representations of n by
$X^2+XY+ \frac {1+d}{4} Y^2$
must necessarily have Y being even. Thus, in this case the representations of n by
![]() $X^2+XY + \frac {1+d}{4} Y^2$
equal the representations of n by
$X^2+XY + \frac {1+d}{4} Y^2$
equal the representations of n by
![]() $x^2+dy^2$
, and assertion (3) follows.
$x^2+dy^2$
, and assertion (3) follows.
4 Proof of the upper bound
In this section, we prove Theorem 1.3. It will follow from the following proposition.
Proposition 4.1. Let N be large and k an integer in the range (1.1). Let d be a square-free integer with
![]() $d\leq \log N$
. Then the number of integers
$d\leq \log N$
. Then the number of integers
![]() $n \in {\mathcal A}(N,k)$
that are represented by
$n \in {\mathcal A}(N,k)$
that are represented by
![]() $x^2+dy^2$
is
$x^2+dy^2$
is
![]() $\ll \frac {N}{2^k} (\log \log N)^3$
.
$\ll \frac {N}{2^k} (\log \log N)^3$
.
Before proving the proposition, let us deduce Theorem 1.3. Note that if
![]() $d=d_1 d_2^2$
with
$d=d_1 d_2^2$
with
![]() $d_1$
square-free, then an integer represented by
$d_1$
square-free, then an integer represented by
![]() $x^2 +dy^2$
is automatically represented by
$x^2 +dy^2$
is automatically represented by
![]() $x^2 +d_1 y^2$
.
$x^2 +d_1 y^2$
.
Using Proposition 4.1, it follows that the number of integers in
![]() ${\mathcal A}(N,k)$
that are represented by
${\mathcal A}(N,k)$
that are represented by
![]() $x^2+dy^2$
for some d,
$x^2+dy^2$
for some d,
![]() $1\leq d\leq \Delta $
is
$1\leq d\leq \Delta $
is
since
![]() $\Delta \leq 2^k/k^4$
. This establishes Theorem 1.3.
$\Delta \leq 2^k/k^4$
. This establishes Theorem 1.3.
To prove Proposition 4.1, we require the following simple lemma.
Lemma 4.2. Let D be any fundamental discriminant apart from
![]() $D=1$
. For all
$D=1$
. For all
![]() $x\geq 1$
, we have
$x\geq 1$
, we have
![]() $\sum _{n\leq x} (1*\chi _D)(n) \ll x\log |D|$
.
$\sum _{n\leq x} (1*\chi _D)(n) \ll x\log |D|$
.
Proof. Suppose first that
![]() $x\leq |D|^2$
. Since
$x\leq |D|^2$
. Since
![]() $(1*\chi _D)(n) \leq \tau (n)$
(the number of divisors of n), the sum in question is
$(1*\chi _D)(n) \leq \tau (n)$
(the number of divisors of n), the sum in question is
![]() $\leq \sum _{n\leq x} \tau (n) \ll x \log (x+1) \ll x\log |D|$
.
$\leq \sum _{n\leq x} \tau (n) \ll x \log (x+1) \ll x\log |D|$
.
Now, suppose that
![]() $x> |D|^2$
, and note that
$x> |D|^2$
, and note that
 $$ \begin{align*}(1*\chi_D)(n) = \sum_{ab =n} \chi_D(b) = \sum_{\substack{ab =n \\ b \leq |D|}}\chi_D(b) + \sum_{\substack{ab=n \\ b>|D|}} \chi_D(b). \end{align*} $$
$$ \begin{align*}(1*\chi_D)(n) = \sum_{ab =n} \chi_D(b) = \sum_{\substack{ab =n \\ b \leq |D|}}\chi_D(b) + \sum_{\substack{ab=n \\ b>|D|}} \chi_D(b). \end{align*} $$
Therefore,
 $$ \begin{align} \sum_{n\leq x} (1*\chi_D)(n) = \sum_{b\leq |D|} \chi_D(b) \sum_{a\leq x/b} 1 + \sum_{a\leq x/|D|} \sum_{|D| < b\leq x/a} \chi_D(b). \end{align} $$
$$ \begin{align} \sum_{n\leq x} (1*\chi_D)(n) = \sum_{b\leq |D|} \chi_D(b) \sum_{a\leq x/b} 1 + \sum_{a\leq x/|D|} \sum_{|D| < b\leq x/a} \chi_D(b). \end{align} $$
The first term on the right side of (4.1) contributes
 $$ \begin{align*}\sum_{b\leq |D|} \chi_D(b) \Big( \frac{x}{b}+O(1)\Big) \ll \sum_{b\leq |D|} \Big( \frac{x}{b}+1\Big) \ll x \log |D|. \end{align*} $$
$$ \begin{align*}\sum_{b\leq |D|} \chi_D(b) \Big( \frac{x}{b}+O(1)\Big) \ll \sum_{b\leq |D|} \Big( \frac{x}{b}+1\Big) \ll x \log |D|. \end{align*} $$
Since
![]() $\chi _D$
is a nonprincipal character to the modulus
$\chi _D$
is a nonprincipal character to the modulus
![]() $|D|$
, it sums to zero over any interval of length D, and therefore
$|D|$
, it sums to zero over any interval of length D, and therefore
![]() $|\sum _{|D| < b\leq x/a} \chi _D(b)| \leq |D|$
. It follows that the second term on the right side of (4.1) contributes
$|\sum _{|D| < b\leq x/a} \chi _D(b)| \leq |D|$
. It follows that the second term on the right side of (4.1) contributes
![]() $\ll |D| \sum _{a\leq x/|D|} 1 \ll x$
, and the lemma follows.
$\ll |D| \sum _{a\leq x/|D|} 1 \ll x$
, and the lemma follows.
Proof of Proposition 4.1
Let d be square-free with
![]() $d \leq \log N$
, and let D be the fundamental discriminant associated to it (as given in (3.5)). Write
$d \leq \log N$
, and let D be the fundamental discriminant associated to it (as given in (3.5)). Write
![]() $\mathcal {R} = \mathcal {R}(d)$
for the set of all r such that the primes dividing r either divide
$\mathcal {R} = \mathcal {R}(d)$
for the set of all r such that the primes dividing r either divide
![]() $|D|$
or appear to exponent at least
$|D|$
or appear to exponent at least
![]() $2$
in the prime factorization of r. Suppose
$2$
in the prime factorization of r. Suppose
![]() $n \in {\mathcal A}(N,k)$
is an integer that can be expressed as
$n \in {\mathcal A}(N,k)$
is an integer that can be expressed as
![]() $x^2+dy^2$
. Write n uniquely as
$x^2+dy^2$
. Write n uniquely as
![]() $rs$
, where
$rs$
, where
![]() $(r,s)=1$
, s is square-free and composed of primes not dividing
$(r,s)=1$
, s is square-free and composed of primes not dividing
![]() $|D|$
and
$|D|$
and
![]() $r \in \mathcal {R}$
. We have that
$r \in \mathcal {R}$
. We have that
![]() $\Omega (r) \leq k$
and note that
$\Omega (r) \leq k$
and note that
![]() $\Omega (s) = k-\Omega (r)$
.
$\Omega (s) = k-\Omega (r)$
.
By Lemma 3.1 and (3.1), we know that if n is representable by
![]() $x^2+dy^2$
, then
$x^2+dy^2$
, then
![]() $(1*\chi _D)(n) \geq R_D(n)>0$
. Since
$(1*\chi _D)(n) \geq R_D(n)>0$
. Since
![]() $(1*\chi _D)$
is a nonnegative multiplicative function, it follows that
$(1*\chi _D)$
is a nonnegative multiplicative function, it follows that
![]() $(1*\chi _D)(s)> 0$
or, equivalently, that every prime
$(1*\chi _D)(s)> 0$
or, equivalently, that every prime
![]() $p|s$
satisfies
$p|s$
satisfies
![]() $\chi _D(p)=1$
and therefore
$\chi _D(p)=1$
and therefore
![]() $(1*\chi _D)(s) = 2^{\Omega (s)}$
. Thus,
$(1*\chi _D)(s) = 2^{\Omega (s)}$
. Thus,
 $$ \begin{align*} \sum_{\substack{ n \in {\mathcal A}(N,k) \\ n =x^2 +dy^2}} 1 \leq \sum_{\substack{ rs \in {\mathcal A}(N,k)}} 2^{-\Omega(s)} (1*\chi_D)(s) & = 2^{-k} \sum_{ rs \in {\mathcal A}(N,k)} 2^{\Omega(r)} (1*\chi_D)(s) \\ & \leq 2^{-k} \sum_{\substack{ r \in \mathcal{R} \\ \Omega(r) \leq k \\ r \leq N} } 2^{\Omega(r)} \sum_{s \leq N/r} (1*\chi_D)(s), \end{align*} $$
$$ \begin{align*} \sum_{\substack{ n \in {\mathcal A}(N,k) \\ n =x^2 +dy^2}} 1 \leq \sum_{\substack{ rs \in {\mathcal A}(N,k)}} 2^{-\Omega(s)} (1*\chi_D)(s) & = 2^{-k} \sum_{ rs \in {\mathcal A}(N,k)} 2^{\Omega(r)} (1*\chi_D)(s) \\ & \leq 2^{-k} \sum_{\substack{ r \in \mathcal{R} \\ \Omega(r) \leq k \\ r \leq N} } 2^{\Omega(r)} \sum_{s \leq N/r} (1*\chi_D)(s), \end{align*} $$
where in the last step we used the nonnegativity of
![]() $1*\chi _D$
to take the sum over all
$1*\chi _D$
to take the sum over all
![]() $s \leq N/r$
. Applying Lemma 4.2 to the sum over s, we obtain
$s \leq N/r$
. Applying Lemma 4.2 to the sum over s, we obtain
 $$ \begin{align*}\sum_{\substack{ n \in {\mathcal A}(N,k) \\ n =x^2 +dy^2}} 1 \ll \frac{N}{2^k} \log |D| \sum_{\substack{r \in \mathcal{R} \\ \Omega(r) \leq k} } \frac{2^{\Omega(r)}}{r}. \end{align*} $$
$$ \begin{align*}\sum_{\substack{ n \in {\mathcal A}(N,k) \\ n =x^2 +dy^2}} 1 \ll \frac{N}{2^k} \log |D| \sum_{\substack{r \in \mathcal{R} \\ \Omega(r) \leq k} } \frac{2^{\Omega(r)}}{r}. \end{align*} $$
Now,
 $$\begin{align*}\sum_{\substack{r \in \mathcal{R} \\ \Omega(r) \leq k}} \frac{2^{\Omega(r)}}{r} \leq \prod_{p| |D|} \Big( 1 + \sum_{j=1}^{k} \frac{2^j}{p^j} \Big) \prod_{p \nmid |D|} \Big(1 +\sum_{j=2}^{k} \frac{2^j}{p^j}\Big) \ll k \prod_{p| |D|} \Big(1 + \frac 2p\Big) \ll k (\log \log |D|)^2, \end{align*}$$
$$\begin{align*}\sum_{\substack{r \in \mathcal{R} \\ \Omega(r) \leq k}} \frac{2^{\Omega(r)}}{r} \leq \prod_{p| |D|} \Big( 1 + \sum_{j=1}^{k} \frac{2^j}{p^j} \Big) \prod_{p \nmid |D|} \Big(1 +\sum_{j=2}^{k} \frac{2^j}{p^j}\Big) \ll k \prod_{p| |D|} \Big(1 + \frac 2p\Big) \ll k (\log \log |D|)^2, \end{align*}$$
where the factor k above arises from the prime
![]() $p=2$
. Since
$p=2$
. Since
![]() $k\ll \log \log N$
and
$k\ll \log \log N$
and
![]() $|D|\leq \log N$
, the proposition follows.
$|D|\leq \log N$
, the proposition follows.
5 Plan of the proof of the lower bound
We now turn to the proof of Theorem 1.4, which constitutes the bulk of the paper. Let N be large, recall that k is an integer in the range (1.1), and suppose in all that follows that
We wish to bound the exceptional integers
![]() $n \in {\mathcal A}(N,k)$
that cannot be represented as
$n \in {\mathcal A}(N,k)$
that cannot be represented as
![]() $x^2+dy^2$
with d below
$x^2+dy^2$
with d below
![]() $\Delta $
. In fact, we shall consider only representations by such quadratic forms when d is a prime lying in a suitable residue class and show that most integers can be represented even with this further constraint.
$\Delta $
. In fact, we shall consider only representations by such quadratic forms when d is a prime lying in a suitable residue class and show that most integers can be represented even with this further constraint.
To state our results more precisely, we distinguish two cases according to whether the
![]() $2$
-adic valuation
$2$
-adic valuation
![]() $v_2(n)$
is
$v_2(n)$
is
![]() $0$
or
$0$
or
![]() $1$
(or in other words whether
$1$
(or in other words whether
![]() $n\equiv 1 \ (\operatorname {mod}\, 2)$
or
$n\equiv 1 \ (\operatorname {mod}\, 2)$
or
![]() $n \equiv 2 \ (\operatorname {mod}\, 4)$
). Results for integers n that are multiples of
$n \equiv 2 \ (\operatorname {mod}\, 4)$
). Results for integers n that are multiples of
![]() $4$
will be deduced easily from these cases. Thus, we define, for all
$4$
will be deduced easily from these cases. Thus, we define, for all
![]() $j =0$
,
$j =0$
,
![]() $1$
,
$1$
,
 $$\begin{align*}{\mathcal A}_j(k) & = \{ v_2(n) = j, \ \ \Omega(n)=k\}, \\ {\mathcal A}_j(N,k) &= \{ n \leq N, \ \ n \in {\mathcal A}_j(k)\}. \end{align*}$$
$$\begin{align*}{\mathcal A}_j(k) & = \{ v_2(n) = j, \ \ \Omega(n)=k\}, \\ {\mathcal A}_j(N,k) &= \{ n \leq N, \ \ n \in {\mathcal A}_j(k)\}. \end{align*}$$
Observe that
and
Thus, from Lemma 1.2 we may deduce that for k satisfying
![]() $|k-k_0| \leq \frac 13 k_0$
we have
$|k-k_0| \leq \frac 13 k_0$
we have
 $$ \begin{align} \mathcal{A}_j(N,k) = 2^{-j-1}\frac{N}{\log N} \frac{k_0^{k}}{k!} \Big(1 + O\Big(\frac{1+|k-k_0|}{k_0}\Big)\Big). \end{align} $$
$$ \begin{align} \mathcal{A}_j(N,k) = 2^{-j-1}\frac{N}{\log N} \frac{k_0^{k}}{k!} \Big(1 + O\Big(\frac{1+|k-k_0|}{k_0}\Big)\Big). \end{align} $$
Here, we recall that
![]() $k_0$
denotes
$k_0$
denotes
![]() $\log \log N$
.
$\log \log N$
.
To each case
![]() $j = 0,1$
we associate a set
$j = 0,1$
we associate a set
![]() $\mathcal {D}_j$
of primes. Below, we let W denote a parameter tending to infinity slowly with N; for definiteness, we set
$\mathcal {D}_j$
of primes. Below, we let W denote a parameter tending to infinity slowly with N; for definiteness, we set
![]() $W=\log \log \log N$
. With this choice of W, define
$W=\log \log \log N$
. With this choice of W, define
Here, as usual, D denotes the fundamental discriminant associated to d as given in (3.5). Thus,
![]() $D=-d$
for
$D=-d$
for
![]() $d\in {\mathcal D}_0$
and since
$d\in {\mathcal D}_0$
and since
![]() $D\equiv 1 \ (\operatorname {mod}\, 8)$
, we have
$D\equiv 1 \ (\operatorname {mod}\, 8)$
, we have
![]() $\chi _D(2) =1$
automatically. If d is in
$\chi _D(2) =1$
automatically. If d is in
![]() ${\mathcal D}_1$
, then
${\mathcal D}_1$
, then
![]() $D= -4d$
, and here
$D= -4d$
, and here
![]() $\chi _D(2)=0$
. The primes in
$\chi _D(2)=0$
. The primes in
![]() ${\mathcal D}_0$
lie in
${\mathcal D}_0$
lie in
![]() $\prod _{3\leq p \leq W} \frac {p-1}{2}$
reduced residue classes
$\prod _{3\leq p \leq W} \frac {p-1}{2}$
reduced residue classes
![]() $(\operatorname {mod}\, 8\prod _{3\leq p\leq W} p)$
, while those in
$(\operatorname {mod}\, 8\prod _{3\leq p\leq W} p)$
, while those in
![]() ${\mathcal D}_1$
lie in
${\mathcal D}_1$
lie in
![]() $\prod _{3\leq p \leq W} \frac {p-1}{2}$
reduced residue classes
$\prod _{3\leq p \leq W} \frac {p-1}{2}$
reduced residue classes
![]() $(\operatorname {mod}\, 4\prod _{3\leq p\leq W} p)$
. Since W is suitably small, a simple application of the prime number theorem in arithmetic progressions gives
$(\operatorname {mod}\, 4\prod _{3\leq p\leq W} p)$
. Since W is suitably small, a simple application of the prime number theorem in arithmetic progressions gives
In particular, since
![]() $W = \log \log \log N$
, and since
$W = \log \log \log N$
, and since
we have the crude bounds
We are now ready to state our result on representing integers in
![]() ${\mathcal A}_j(N,k)$
using the binary quadratic forms
${\mathcal A}_j(N,k)$
using the binary quadratic forms
![]() $x^2 + dy^2$
with
$x^2 + dy^2$
with
![]() $d\in {\mathcal D}_j$
. From this result, we shall swiftly deduce Theorem 1.4.
$d\in {\mathcal D}_j$
. From this result, we shall swiftly deduce Theorem 1.4.
Theorem 5.1. Suppose that N is large, k is an integer in the range
where
![]() $k_0 := \log \log N$
, and that
$k_0 := \log \log N$
, and that
![]() $k^3 2^k \leq \Delta \leq \log N$
. For
$k^3 2^k \leq \Delta \leq \log N$
. For
![]() $j = 0,1$
, let
$j = 0,1$
, let
![]() ${\mathcal E}_j(N,k)$
denote the exceptional set of integers in
${\mathcal E}_j(N,k)$
denote the exceptional set of integers in
![]() ${\mathcal A}_j(N,k)$
that cannot be expressed as
${\mathcal A}_j(N,k)$
that cannot be expressed as
![]() $x^2+dy^2$
for some
$x^2+dy^2$
for some
![]() $d\in {\mathcal D}_j$
. Then we have
$d\in {\mathcal D}_j$
. Then we have
Deducing Theorem 1.4 from Theorem 5.1.
Extracting the largest power of
![]() $4$
, we see that every
$4$
, we see that every
![]() $n \in {\mathcal A}(N,k)$
may be written uniquely as
$n \in {\mathcal A}(N,k)$
may be written uniquely as
![]() $n= 4^m r$
, where r is either in
$n= 4^m r$
, where r is either in
![]() ${\mathcal A}_0(N/4^m, k-2m)$
or in
${\mathcal A}_0(N/4^m, k-2m)$
or in
![]() ${\mathcal A}_1(N/4^m, k-2m)$
. Further, if r can be represented as
${\mathcal A}_1(N/4^m, k-2m)$
. Further, if r can be represented as
![]() $x^2 +dy^2$
with
$x^2 +dy^2$
with
![]() $d\leq \Delta $
, then plainly so can
$d\leq \Delta $
, then plainly so can
![]() $n= 4^m r$
. Thus,
$n= 4^m r$
. Thus,
First, let us dispense with the terms
![]() $m \geq \log k_0$
. Bounding
$m \geq \log k_0$
. Bounding
![]() $|{\mathcal E}_0(N/4^m, k-2m)| + |{\mathcal E}_1(N/4^m, k-2m)|$
trivially by
$|{\mathcal E}_0(N/4^m, k-2m)| + |{\mathcal E}_1(N/4^m, k-2m)|$
trivially by
![]() $N/4^m$
, we see that these terms contribute
$N/4^m$
, we see that these terms contribute
![]() $\ll \sum _{m\geq \log k_0} N/4^m \ll N/k_0$
, which is better than we need.
$\ll \sum _{m\geq \log k_0} N/4^m \ll N/k_0$
, which is better than we need.
For the terms with
![]() $m\leq \log k_0$
, we wish to use Theorem 5.1 to bound the quantity
$m\leq \log k_0$
, we wish to use Theorem 5.1 to bound the quantity
![]() $|{\mathcal E}_j (N/4^m, k-2m)|$
(for
$|{\mathcal E}_j (N/4^m, k-2m)|$
(for
![]() $j=0,1$
). We must check that the required conditions there hold. The condition on
$j=0,1$
). We must check that the required conditions there hold. The condition on
![]() $\Delta $
is automatic: Since
$\Delta $
is automatic: Since
![]() $\Delta $
is assumed to be
$\Delta $
is assumed to be
![]() $\geq k^3 2^k$
it is clearly also
$\geq k^3 2^k$
it is clearly also
![]() $\geq (k-2m)^3 2^{k-2m}$
. The main condition to check is the analogue of (5.5) which here reads
$\geq (k-2m)^3 2^{k-2m}$
. The main condition to check is the analogue of (5.5) which here reads
![]() $|(k-2m) - \log \log (N/4^m) | \leq 2 (\log \log (N/4^m))^{2/3}$
. To verify this, note that for
$|(k-2m) - \log \log (N/4^m) | \leq 2 (\log \log (N/4^m))^{2/3}$
. To verify this, note that for
![]() $m\leq \log k_0$
, one has
$m\leq \log k_0$
, one has
![]() $\log \log (N/4^m) = k_0 +O(1)$
, and so the left side above is
$\log \log (N/4^m) = k_0 +O(1)$
, and so the left side above is
![]() $\leq |k_0 - k| + 2m + O(1) \leq k_0^{2/3} + 2\log k_0 + O(1)$
since k is in the range (1.1). Thus, we may apply Theorem 5.1, and conclude that
$\leq |k_0 - k| + 2m + O(1) \leq k_0^{2/3} + 2\log k_0 + O(1)$
since k is in the range (1.1). Thus, we may apply Theorem 5.1, and conclude that
Now, applying Lemma 1.2 we obtain
 $$ \begin{align*} |{\mathcal A} (N/4^m, k-2m)| & \ll \frac{N}{4^m \log (N/4^m)} \frac{(\log \log (N/4^m))^{k-2m}}{(k-2m)!} \\ & \ll \frac{N}{4^m \log N} \frac{(\log \log N)^{k-2m}}{(k-2m)!} \ll \frac{N}{4^m \log N} \frac{k_0^{k}}{k!} \Big(\frac{k}{k_0}\Big)^{2m} \ll \frac{|{\mathcal A}(N,k)|}{4^m}, \end{align*} $$
$$ \begin{align*} |{\mathcal A} (N/4^m, k-2m)| & \ll \frac{N}{4^m \log (N/4^m)} \frac{(\log \log (N/4^m))^{k-2m}}{(k-2m)!} \\ & \ll \frac{N}{4^m \log N} \frac{(\log \log N)^{k-2m}}{(k-2m)!} \ll \frac{N}{4^m \log N} \frac{k_0^{k}}{k!} \Big(\frac{k}{k_0}\Big)^{2m} \ll \frac{|{\mathcal A}(N,k)|}{4^m}, \end{align*} $$
where the final estimate holds since
![]() $k/k_0 = 1 +O(k_0^{-1/3})$
and
$k/k_0 = 1 +O(k_0^{-1/3})$
and
![]() $m\leq \log k_0$
so that
$m\leq \log k_0$
so that
![]() $(k/k_0)^{2m} \ll 1$
. We conclude that the contribution of the terms with
$(k/k_0)^{2m} \ll 1$
. We conclude that the contribution of the terms with
![]() $m \leq \log k_0$
may be bounded by
$m \leq \log k_0$
may be bounded by
 $$ \begin{align*}\ll \sum_{m\leq \log k_0} 4^{-m} \Big( \frac{|{\mathcal A}(N,k)|}{\log k_0} + N k^{\varepsilon - 5/6}\Big) \ll \frac{|{\mathcal A}(N,k)|}{\log k_0} + N k_0^{-3/4}. \end{align*} $$
$$ \begin{align*}\ll \sum_{m\leq \log k_0} 4^{-m} \Big( \frac{|{\mathcal A}(N,k)|}{\log k_0} + N k^{\varepsilon - 5/6}\Big) \ll \frac{|{\mathcal A}(N,k)|}{\log k_0} + N k_0^{-3/4}. \end{align*} $$
Combining this estimate with our bound for the larger range of m, we complete the deduction of Theorem 1.4.
Theorem 5.1 will be deduced (in the next section) from the following four propositions which form the heart of our argument. Before stating these propositions, we introduce some notation that will be in place for the rest of our work. We shall factorize n as
![]() $n^{\flat } n^{\sharp }$
, where
$n^{\flat } n^{\sharp }$
, where
![]() $n^{\flat }$
is composed only of primes below W, and
$n^{\flat }$
is composed only of primes below W, and
![]() $n^{\sharp }$
is composed only of primes above W. Further, we define
$n^{\sharp }$
is composed only of primes above W. Further, we define
For each choice of
![]() $j=0$
or
$j=0$
or
![]() $1$
, we define
$1$
, we define
 $$ \begin{align} F_j(n) = \frac{1}{|{\mathcal D}_j|} \sum_{d\in {\mathcal D}_j} \frac{|D|^{1/2}}{\pi \gamma_W} \frac{R_D(n)}{\tau(n^{\flat})}. \end{align} $$
$$ \begin{align} F_j(n) = \frac{1}{|{\mathcal D}_j|} \sum_{d\in {\mathcal D}_j} \frac{|D|^{1/2}}{\pi \gamma_W} \frac{R_D(n)}{\tau(n^{\flat})}. \end{align} $$
Note that if n cannot be represented as
![]() $x^2 +dy^2$
with
$x^2 +dy^2$
with
![]() $d\in {\mathcal D}_j$
, then
$d\in {\mathcal D}_j$
, then
![]() $R_D(n)=0$
for all
$R_D(n)=0$
for all
![]() $d\in {\mathcal D}_j$
and therefore
$d\in {\mathcal D}_j$
and therefore
![]() $F_j(n)=0$
. The proof is based on showing that for
$F_j(n)=0$
. The proof is based on showing that for
![]() $n\in {\mathcal A}_j(k)$
, the quantity
$n\in {\mathcal A}_j(k)$
, the quantity
![]() $F_j(n)$
is usually close to its expected value of
$F_j(n)$
is usually close to its expected value of
![]() $1$
, which is achieved by showing that
$1$
, which is achieved by showing that
![]() $(F_j(n)-1)^2$
is small on average over n. The four propositions below facilitate the calculation of this variance, which will be carried out in the next section.
$(F_j(n)-1)^2$
is small on average over n. The four propositions below facilitate the calculation of this variance, which will be carried out in the next section.
Proposition 5.2. Let N be large, and let k be an integer in the range (5.5). The following statements hold for either choice of
![]() $j=0$
or
$j=0$
or
![]() $1$
. Let d be an element in
$1$
. Let d be an element in
![]() ${\mathcal D}_j$
, and let D be the corresponding fundamental discriminant. Then
${\mathcal D}_j$
, and let D be the corresponding fundamental discriminant. Then
 $$\begin{align*}\frac{|D|^{1/2}}{\pi \gamma_W} \sum_{n \in {\mathcal A}_j(k)} \frac{R_D(n)}{\tau(n^{\flat})} e^{-n/N} = \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} + N O_{\varepsilon}\big( k_0^{\varepsilon - 5/6} + L(1,\chi_D)^{-1} k_0^{-2}\big), \end{align*}$$
$$\begin{align*}\frac{|D|^{1/2}}{\pi \gamma_W} \sum_{n \in {\mathcal A}_j(k)} \frac{R_D(n)}{\tau(n^{\flat})} e^{-n/N} = \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} + N O_{\varepsilon}\big( k_0^{\varepsilon - 5/6} + L(1,\chi_D)^{-1} k_0^{-2}\big), \end{align*}$$
where
![]() $\gamma _W$
is as in (5.6).
$\gamma _W$
is as in (5.6).
Partial summation and (5.1) easily allow us to give an asymptotic for the sum
![]() $\sum _{n\in {\mathcal A}_j(k)} e^{-n/N}$
appearing above. Write
$\sum _{n\in {\mathcal A}_j(k)} e^{-n/N}$
appearing above. Write
 $$\begin{align*}\sum_{n\in {\mathcal A}_j(k)} e^{-n/N} = \int^{\infty}_0 e^{-u} |\mathcal{A}_j(uN, k)| du = \int_{1/\log N}^{\log N} e^{-u} |{\mathcal A}_j(uN,k)| du + O\big(\frac{N}{\log N}\big), \end{align*}$$
$$\begin{align*}\sum_{n\in {\mathcal A}_j(k)} e^{-n/N} = \int^{\infty}_0 e^{-u} |\mathcal{A}_j(uN, k)| du = \int_{1/\log N}^{\log N} e^{-u} |{\mathcal A}_j(uN,k)| du + O\big(\frac{N}{\log N}\big), \end{align*}$$
where we truncated the integral above using the trivial bound
![]() $|{\mathcal A}_j(uN,k)| \leq uN$
in the range
$|{\mathcal A}_j(uN,k)| \leq uN$
in the range
![]() $u \not \in [1/\log N, \log N]$
. Now, using (5.1) for
$u \not \in [1/\log N, \log N]$
. Now, using (5.1) for
![]() $u \in [1/\log N, \log N]$
and the estimate
$u \in [1/\log N, \log N]$
and the estimate
![]() $\frac {k_0^k}{k!} \ll k_0^{-1/2} \log N$
, which follows from (2.3), we obtain that for k in the range (5.5)
$\frac {k_0^k}{k!} \ll k_0^{-1/2} \log N$
, which follows from (2.3), we obtain that for k in the range (5.5)
 $$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} = 2^{-j - 1} \frac{N}{\log N} \frac{k_0 ^{k}}{k!} + O( N k_0^{-5/6}). \end{align} $$
$$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} = 2^{-j - 1} \frac{N}{\log N} \frac{k_0 ^{k}}{k!} + O( N k_0^{-5/6}). \end{align} $$
Note that there is a small subtlety in the application of (5.1), which is that N must be replaced by
![]() $uN$
not only in the obvious term
$uN$
not only in the obvious term
![]() $\frac {N}{\log N}$
, but also
$\frac {N}{\log N}$
, but also
![]() $k_0$
must be replaced by
$k_0$
must be replaced by
![]() $\log \log (uN)$
. We leave it to the reader to check that these changes have negligible effect for u in the stated range.
$\log \log (uN)$
. We leave it to the reader to check that these changes have negligible effect for u in the stated range.
Our next proposition considers averages of
![]() $R_D(n) R_{\tilde D}(n)$
for two different elements d,
$R_D(n) R_{\tilde D}(n)$
for two different elements d,
![]() ${\widetilde d} \in {\mathcal D}_j$
. The answer will involve the character
${\widetilde d} \in {\mathcal D}_j$
. The answer will involve the character
![]() $\chi _{d {\tilde d}}$
, which we now briefly introduce. Since d and
$\chi _{d {\tilde d}}$
, which we now briefly introduce. Since d and
![]() ${\tilde d}$
are different primes that are congruent to each other
${\tilde d}$
are different primes that are congruent to each other
![]() $(\operatorname {mod}\, 4)$
, it follows that
$(\operatorname {mod}\, 4)$
, it follows that
![]() $d{\tilde d} \equiv 1 \ (\operatorname {mod}\, 4)$
is a fundamental discriminant, and so the Kronecker symbol
$d{\tilde d} \equiv 1 \ (\operatorname {mod}\, 4)$
is a fundamental discriminant, and so the Kronecker symbol
![]() $\chi _{d {\tilde d}}$
is a primitive character to the modulus
$\chi _{d {\tilde d}}$
is a primitive character to the modulus
![]() $d{\tilde d}$
. This character is also closely connected to the product of characters
$d{\tilde d}$
. This character is also closely connected to the product of characters
![]() $\chi _D \chi _{\tilde D}$
. Indeed, in the case
$\chi _D \chi _{\tilde D}$
. Indeed, in the case
![]() $j=0$
both characters are identical, and in the case
$j=0$
both characters are identical, and in the case
![]() $j=1$
the character
$j=1$
the character
![]() $\chi _D \chi _{\tilde D}$
is the imprimitive character
$\chi _D \chi _{\tilde D}$
is the imprimitive character
![]() $(\operatorname {mod}\, 4d{\tilde d})$
induced by the primitive character
$(\operatorname {mod}\, 4d{\tilde d})$
induced by the primitive character
![]() $\chi _{d {\tilde d}}$
.
$\chi _{d {\tilde d}}$
.
Proposition 5.3. Let N be large, and let k be an integer in the range (5.5). Let j be
![]() $0$
or
$0$
or
![]() $1$
. Let d and
$1$
. Let d and
![]() ${\widetilde d}$
be two different elements in
${\widetilde d}$
be two different elements in
![]() ${\mathcal D}_j$
, and let D and
${\mathcal D}_j$
, and let D and
![]() $\widetilde {D}$
denote the corresponding fundamental discriminants. If
$\widetilde {D}$
denote the corresponding fundamental discriminants. If
![]() $d\equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
(which is automatic when
$d\equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
(which is automatic when
![]() $j=0$
), then
$j=0$
), then
 $$ \begin{align} \frac{|D{\widetilde D}|^{1/2} }{\pi^2 \gamma_W^2} \sum_{n \in {\mathcal A}_j(k)} & \frac{R_D(n) R_{\tilde D}(n)}{\tau(n^{\flat})^2} e^{-n/N} = \big(2^j + O(W^{-1})\big)\gamma_W L(1,\chi_{d{\widetilde d}}) \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} \nonumber\\ & + NO_{\varepsilon}\Big( L(1,\chi_{d{\widetilde d}})k_0^{\varepsilon - 5/6} + L(1,\chi_D)^{-1} L(1, \chi_{\tilde D})^{-1} k_0^{\varepsilon - 3}\Big), \end{align} $$
$$ \begin{align} \frac{|D{\widetilde D}|^{1/2} }{\pi^2 \gamma_W^2} \sum_{n \in {\mathcal A}_j(k)} & \frac{R_D(n) R_{\tilde D}(n)}{\tau(n^{\flat})^2} e^{-n/N} = \big(2^j + O(W^{-1})\big)\gamma_W L(1,\chi_{d{\widetilde d}}) \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} \nonumber\\ & + NO_{\varepsilon}\Big( L(1,\chi_{d{\widetilde d}})k_0^{\varepsilon - 5/6} + L(1,\chi_D)^{-1} L(1, \chi_{\tilde D})^{-1} k_0^{\varepsilon - 3}\Big), \end{align} $$
while if
![]() $d \not \equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
(which can only happen for
$d \not \equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
(which can only happen for
![]() $j=1$
), then
$j=1$
), then
 $$ \begin{align} \sum_{n \in {\mathcal A}_j(k)} \frac{R_D(n) R_{\tilde D}(n)}{\tau(n^{\flat})^2} e^{-n/N} =0. \end{align} $$
$$ \begin{align} \sum_{n \in {\mathcal A}_j(k)} \frac{R_D(n) R_{\tilde D}(n)}{\tau(n^{\flat})^2} e^{-n/N} =0. \end{align} $$
The next proposition concerns the case when
![]() $d = {\widetilde d}$
, where an upper bound suffices.
$d = {\widetilde d}$
, where an upper bound suffices.
Proposition 5.4. Let N be large, and let k be an integer in the range (5.5). Let
![]() $j=0$
or
$j=0$
or
![]() $1$
, and let d be an element of
$1$
, and let d be an element of
![]() ${\mathcal D}_j$
with D denoting the corresponding fundamental discriminant. Then we have
${\mathcal D}_j$
with D denoting the corresponding fundamental discriminant. Then we have
 $$\begin{align*}\frac{|D|}{\pi^2 \gamma_W^2} \sum_{n \in {\mathcal A}_j(k)} \frac{R_D(n)^2}{\tau(n^{\flat})^2} e^{-n/N} \ll \frac{2^k N}{\gamma_W L(1,\chi_D)} \big( k_0^{-1/2} + L(1,\chi_D)^{-1}k_0^{-2}\big) + |D|^{1/2} (\log |D|)^3 N. \end{align*}$$
$$\begin{align*}\frac{|D|}{\pi^2 \gamma_W^2} \sum_{n \in {\mathcal A}_j(k)} \frac{R_D(n)^2}{\tau(n^{\flat})^2} e^{-n/N} \ll \frac{2^k N}{\gamma_W L(1,\chi_D)} \big( k_0^{-1/2} + L(1,\chi_D)^{-1}k_0^{-2}\big) + |D|^{1/2} (\log |D|)^3 N. \end{align*}$$
Finally, to complete our calculation of the average of
![]() $(F_j(n)-1)^2$
, we shall need an asymptotic for the the average of
$(F_j(n)-1)^2$
, we shall need an asymptotic for the the average of
![]() $L(1,\chi _{d{\widetilde d}})$
appearing in Proposition 5.3.
$L(1,\chi _{d{\widetilde d}})$
appearing in Proposition 5.3.
Proposition 5.5. For each
![]() $j=0,1$
, we have
$j=0,1$
, we have
 $$ \begin{align*}\frac{1}{|\mathcal{D}_j|^{2}} \sum_{\substack{ d \neq \tilde{d} \in {\mathcal D}_j \\ d\equiv {\tilde d} \ (\operatorname{mod}\, 8)} } L(1,\chi_{d\tilde{d}}) = \frac{1}{\gamma_W} \big(2^{-j}+ O(W^{-1})\big). \end{align*} $$
$$ \begin{align*}\frac{1}{|\mathcal{D}_j|^{2}} \sum_{\substack{ d \neq \tilde{d} \in {\mathcal D}_j \\ d\equiv {\tilde d} \ (\operatorname{mod}\, 8)} } L(1,\chi_{d\tilde{d}}) = \frac{1}{\gamma_W} \big(2^{-j}+ O(W^{-1})\big). \end{align*} $$
6 Deducing Theorem 5.1 from Propositions 5.2, 5.3, 5.4 and 5.5
We now deduce Theorem 5.1 from the four propositions enunciated in the previous section. Let j be
![]() $0$
or
$0$
or
![]() $1$
, and k an integer in the range (5.5). Recall from (5.7) the definition of
$1$
, and k an integer in the range (5.5). Recall from (5.7) the definition of
![]() $F_j(n)$
, and recall that
$F_j(n)$
, and recall that
![]() $F_j(n) =0$
if n cannot be represented as
$F_j(n) =0$
if n cannot be represented as
![]() $x^2+dy^2$
with
$x^2+dy^2$
with
![]() $d\in {\mathcal D}_j$
. Therefore, writing
$d\in {\mathcal D}_j$
. Therefore, writing
![]() ${\mathcal E}_j(N,k)$
for the exceptional set as in Theorem 5.1,
${\mathcal E}_j(N,k)$
for the exceptional set as in Theorem 5.1,
 $$ \begin{align} |{\mathcal E}_j(N,k)| \ll \sum_{n\in {\mathcal A}_j(k)} (F_j(n)-1)^2 e^{-n/N} = \sum_{n\in {\mathcal A}_j(k)} (F_j(n)^2 - 2 F_j(n) +1) e^{-n/N}. \end{align} $$
$$ \begin{align} |{\mathcal E}_j(N,k)| \ll \sum_{n\in {\mathcal A}_j(k)} (F_j(n)-1)^2 e^{-n/N} = \sum_{n\in {\mathcal A}_j(k)} (F_j(n)^2 - 2 F_j(n) +1) e^{-n/N}. \end{align} $$
We now invoke Propositions 5.2, 5.3, 5.4 and 5.5 to bound the right side above. To handle some error terms that arise, we require bounds for the average values of
![]() $L(1,\chi _D)^{-m}$
with
$L(1,\chi _D)^{-m}$
with
![]() $m=1$
and
$m=1$
and
![]() $2$
. Although we can be more precise, it suffices to use [Reference Granville and Soundararajan11, Theorem 2] and (5.4) to obtain
$2$
. Although we can be more precise, it suffices to use [Reference Granville and Soundararajan11, Theorem 2] and (5.4) to obtain
 $$ \begin{align} \frac{1}{|\mathcal{D}_j|}\sum_{d\in {\mathcal D}_j} L(1,\chi_D)^{-m} \leq \frac{1}{|\mathcal{D}_j|}\sum_{\substack{d \leq \Delta \\ d\text{ odd} \\ \mu^2(d) = 1}} L(1,\chi_D)^{-m} \ll \frac{\Delta}{|\mathcal{D}_j|} \ll (\log \Delta)^{1 + o(1)} \end{align} $$
$$ \begin{align} \frac{1}{|\mathcal{D}_j|}\sum_{d\in {\mathcal D}_j} L(1,\chi_D)^{-m} \leq \frac{1}{|\mathcal{D}_j|}\sum_{\substack{d \leq \Delta \\ d\text{ odd} \\ \mu^2(d) = 1}} L(1,\chi_D)^{-m} \ll \frac{\Delta}{|\mathcal{D}_j|} \ll (\log \Delta)^{1 + o(1)} \end{align} $$
for
![]() $j = 0,1$
and
$j = 0,1$
and
![]() $m = 1,2$
.
$m = 1,2$
.
A few further remarks on the application of [Reference Granville and Soundararajan11, Theorem 2] may be helpful. First, since we are dealing with moments where m is bounded (albeit negative) we can exclude the contribution of exceptional characters, as remarked in the paragraph following the statement of [Reference Granville and Soundararajan11, Theorem 2]. Second, denoting by X the random Euler product featuring in the statement of [Reference Granville and Soundararajan11, Theorem 2] then, as remarked in [Reference Granville and Soundararajan11, page 995],
![]() $\mathbf {P}(L(1, X) \leq 1/t)$
decays doubly exponentially as
$\mathbf {P}(L(1, X) \leq 1/t)$
decays doubly exponentially as
![]() $t \rightarrow \infty $
so that the moments
$t \rightarrow \infty $
so that the moments
![]() $\mathbf {E} L(1, X)^{-1}$
and
$\mathbf {E} L(1, X)^{-1}$
and
![]() $\mathbf {E} L(1,X)^{-2}$
are bounded.
$\mathbf {E} L(1,X)^{-2}$
are bounded.
From Proposition 5.2, (6.2) (with
![]() $m = 1$
) and the assumption that
$m = 1$
) and the assumption that
![]() $\Delta \leq \log N$
, it follows that
$\Delta \leq \log N$
, it follows that
 $$ \begin{align} \sum_{n \in{\mathcal A}_j(k)} F_j(n) e^{-n/N} = \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} + O_{\varepsilon}(N k_0^{\varepsilon - 5/6}). \end{align} $$
$$ \begin{align} \sum_{n \in{\mathcal A}_j(k)} F_j(n) e^{-n/N} = \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} + O_{\varepsilon}(N k_0^{\varepsilon - 5/6}). \end{align} $$
It remains to evaluate the terms involving
![]() $F_j(n)^2$
in (6.1). Expanding out the square, we have
$F_j(n)^2$
in (6.1). Expanding out the square, we have
 $$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} F_j(n)^2 e^{-n/N} = \frac{1}{\pi^2 \gamma_W^2 |{\mathcal D}_j|^2} \sum_{d, {\widetilde d} \in {\mathcal D}_j} |D \tilde D|^{1/2} \sum_{n\in {\mathcal A}_j(k)} \frac{R_D(n) R_{\widetilde D}(n)}{\tau(n^{\flat})^2 } e^{-n/N}\kern-1.3pt. \end{align} $$
$$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} F_j(n)^2 e^{-n/N} = \frac{1}{\pi^2 \gamma_W^2 |{\mathcal D}_j|^2} \sum_{d, {\widetilde d} \in {\mathcal D}_j} |D \tilde D|^{1/2} \sum_{n\in {\mathcal A}_j(k)} \frac{R_D(n) R_{\widetilde D}(n)}{\tau(n^{\flat})^2 } e^{-n/N}\kern-1.3pt. \end{align} $$
Here, we separate the diagonal terms
![]() $d={\widetilde d}$
from the off-diagonal terms
$d={\widetilde d}$
from the off-diagonal terms
![]() $d\neq {\widetilde d}$
. By Proposition 5.4, we see that the contribution of the diagonal terms is bounded by
$d\neq {\widetilde d}$
. By Proposition 5.4, we see that the contribution of the diagonal terms is bounded by
 $$ \begin{align*}\ll \frac{N}{|{\mathcal D}_j|^2} \sum_{d\in {\mathcal D}_j} \Big( 2^k \gamma_W^{-1} \big( L(1,\chi_D)^{-1}k_0^{-1/2} + L(1,\chi_D)^{-2} k_0^{-2}\big) + |D|^{1/2} (\log |D|)^3\Big). \end{align*} $$
$$ \begin{align*}\ll \frac{N}{|{\mathcal D}_j|^2} \sum_{d\in {\mathcal D}_j} \Big( 2^k \gamma_W^{-1} \big( L(1,\chi_D)^{-1}k_0^{-1/2} + L(1,\chi_D)^{-2} k_0^{-2}\big) + |D|^{1/2} (\log |D|)^3\Big). \end{align*} $$
Using (5.4) and (6.2), the Mertens bound
![]() $\gamma _W \geq 1/\log W = (\log \Delta )^{-o(1)}$
and that
$\gamma _W \geq 1/\log W = (\log \Delta )^{-o(1)}$
and that
![]() $\Delta \geq k^3 2^k$
, the above is
$\Delta \geq k^3 2^k$
, the above is
As for the off-diagonal terms in (6.4), using Proposition 5.3 we see that their contribution is
 $$ \begin{align*} \frac{1}{|{\mathcal D}_j|^2} \sum_{\substack{ d\neq {\widetilde d} \in {\mathcal D}_j \\ d\equiv {\widetilde d}\ (\operatorname{mod}\, 8)}} \bigg(\big( & 2^j + O(W^{-1})\big) L(1, \chi_{d\widetilde d})\gamma_W \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} \\ &+ NO_{\varepsilon}\big(L(1,\chi_{d{\widetilde d}})^{-1} k_0^{\varepsilon - 5/6} + L(1,\chi_D)^{-1} L(1,\chi_{\widetilde D})^{-1} k_0^{\varepsilon - 3 }\big)\Big). \end{align*} $$
$$ \begin{align*} \frac{1}{|{\mathcal D}_j|^2} \sum_{\substack{ d\neq {\widetilde d} \in {\mathcal D}_j \\ d\equiv {\widetilde d}\ (\operatorname{mod}\, 8)}} \bigg(\big( & 2^j + O(W^{-1})\big) L(1, \chi_{d\widetilde d})\gamma_W \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} \\ &+ NO_{\varepsilon}\big(L(1,\chi_{d{\widetilde d}})^{-1} k_0^{\varepsilon - 5/6} + L(1,\chi_D)^{-1} L(1,\chi_{\widetilde D})^{-1} k_0^{\varepsilon - 3 }\big)\Big). \end{align*} $$
Now, using Proposition 5.5, (6.2) and the bound
![]() $\gamma _W^{-1} \ll (\log \Delta )^{o(1)}$
, the above is
$\gamma _W^{-1} \ll (\log \Delta )^{o(1)}$
, the above is
 $$ \begin{align} \big(1 +O (W^{-1}) \big) \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} + O_{\varepsilon}( N k_0^{\varepsilon - 5/6}). \end{align} $$
$$ \begin{align} \big(1 +O (W^{-1}) \big) \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} + O_{\varepsilon}( N k_0^{\varepsilon - 5/6}). \end{align} $$
Combining (6.5) and (6.6), we conclude that
 $$ \begin{align*}\sum_{n\in {\mathcal A}_j(k)} F_j(n)^2 e^{-n/N} = \big(1 +O(W^{-1}) \big) \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} + O_{\varepsilon}( N k_0^{\varepsilon - 5/6}). \end{align*} $$
$$ \begin{align*}\sum_{n\in {\mathcal A}_j(k)} F_j(n)^2 e^{-n/N} = \big(1 +O(W^{-1}) \big) \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} + O_{\varepsilon}( N k_0^{\varepsilon - 5/6}). \end{align*} $$
Taken together with (6.3), it follows that
 $$\begin{align*}\sum_{n\in {\mathcal A}_j(k)} (F_j(n)-1)^2 e^{-n/N} \ll_{\varepsilon} W^{-1} \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} + N k_0^{\varepsilon - 5/6} \ll W^{-1} |{\mathcal A}(N,k)|+ N k_0^{\varepsilon - 5/6}, \end{align*}$$
$$\begin{align*}\sum_{n\in {\mathcal A}_j(k)} (F_j(n)-1)^2 e^{-n/N} \ll_{\varepsilon} W^{-1} \sum_{n\in {\mathcal A}_j(k)} e^{-n/N} + N k_0^{\varepsilon - 5/6} \ll W^{-1} |{\mathcal A}(N,k)|+ N k_0^{\varepsilon - 5/6}, \end{align*}$$
in view of (5.8) and Lemma 1.2. Using this estimate in (6.1) and recalling that
![]() $W = \log \log \log N = \log k_0$
, Theorem 5.1 follows.
$W = \log \log \log N = \log k_0$
, Theorem 5.1 follows.
7 Proof of Proposition 5.5
In the proof below, it is convenient to set
Suppose d and
![]() ${\widetilde d}$
are distinct elements in
${\widetilde d}$
are distinct elements in
![]() ${\mathcal D}_j$
with
${\mathcal D}_j$
with
![]() $d \equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
. Then
$d \equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
. Then
![]() $d{\widetilde d}$
is a square-free integer
$d{\widetilde d}$
is a square-free integer
![]() $\equiv 1 \ (\operatorname {mod}\, 8)$
and is thus a fundamental discriminant. Since
$\equiv 1 \ (\operatorname {mod}\, 8)$
and is thus a fundamental discriminant. Since
![]() $d{\tilde d}\leq \Delta ^2$
, partial summation and the Pólya–Vinogradov inequality give
$d{\tilde d}\leq \Delta ^2$
, partial summation and the Pólya–Vinogradov inequality give
 $$ \begin{align} L(1,\chi_{d{\tilde d}}) = \sum_{n\leq M} \frac{\chi_{d{\tilde d}}(n)}{n} + \int_{M}^{\infty} \sum_{M< n\leq t} \chi_{d\tilde d}(n) \frac{dt}{t^2} = \sum_{n\leq M} \frac{\chi_{d{\tilde d}}(n)}{n} + O(\Delta^{-1/4}). \end{align} $$
$$ \begin{align} L(1,\chi_{d{\tilde d}}) = \sum_{n\leq M} \frac{\chi_{d{\tilde d}}(n)}{n} + \int_{M}^{\infty} \sum_{M< n\leq t} \chi_{d\tilde d}(n) \frac{dt}{t^2} = \sum_{n\leq M} \frac{\chi_{d{\tilde d}}(n)}{n} + O(\Delta^{-1/4}). \end{align} $$
We first show that (when summed over d and
![]() ${\tilde d}$
) the terms with
${\tilde d}$
) the terms with
![]() $n> K$
contribute a negligible amount. Here, we extend the sum over
$n> K$
contribute a negligible amount. Here, we extend the sum over
![]() $d {\tilde d}$
to all discriminants below
$d {\tilde d}$
to all discriminants below
![]() $\Delta ^2$
that are
$\Delta ^2$
that are
![]() $1 \ (\operatorname {mod}\, 8)$
. Recall that a discriminant is an integer
$1 \ (\operatorname {mod}\, 8)$
. Recall that a discriminant is an integer
![]() $\ell \equiv 0$
or
$\ell \equiv 0$
or
![]() $1 \ (\operatorname {mod}\, 4)$
and that every discriminant
$1 \ (\operatorname {mod}\, 4)$
and that every discriminant
![]() $\ell $
may be written uniquely as
$\ell $
may be written uniquely as
![]() $\ell _0 r^2$
, where
$\ell _0 r^2$
, where
![]() $\ell _0$
is a fundamental discriminant. For every discriminant
$\ell _0$
is a fundamental discriminant. For every discriminant
![]() $\ell $
, we may define the Kronecker symbol
$\ell $
, we may define the Kronecker symbol
![]() $\chi _\ell $
exactly as in Subsection 3.1, and it defines a quadratic character
$\chi _\ell $
exactly as in Subsection 3.1, and it defines a quadratic character
![]() $(\operatorname {mod}\, \ell )$
, possibly imprimitive and induced from the primitive character
$(\operatorname {mod}\, \ell )$
, possibly imprimitive and induced from the primitive character
![]() $\chi _{\ell _0}\kern-1.3pt $
. Thus, using Cauchy–Schwarz, we find
$\chi _{\ell _0}\kern-1.3pt $
. Thus, using Cauchy–Schwarz, we find
 $$\begin{align*}\sum_{\substack{ d, \widetilde{d} \in {\mathcal D}_j \\ d \neq {\widetilde d} \\ d\equiv {\widetilde d} \ (\operatorname{mod}\, 8)}} \Big| \sum_{ K \leq n \leq M} \frac{\chi_{d{\tilde d}}(n)}{n}\Big| &\leq \sum_{\substack{ d\leq \Delta^2 \\ d\equiv 1 \ (\operatorname{mod}\, 8)}} \Big| \sum_{ K \leq n \leq M} \frac{\chi_{d}(n)}{n}\Big| \\ &\leq \Delta \Bigg( \sum_{\substack{ d\leq \Delta^2 \\ d\equiv 1 \ (\operatorname{mod}\, 8)}} \Big| \sum_{K \leq n \leq M} \frac{\chi_{d}(n)}{n}\Big|^2 \Bigg)^{1/2}. \end{align*}$$
$$\begin{align*}\sum_{\substack{ d, \widetilde{d} \in {\mathcal D}_j \\ d \neq {\widetilde d} \\ d\equiv {\widetilde d} \ (\operatorname{mod}\, 8)}} \Big| \sum_{ K \leq n \leq M} \frac{\chi_{d{\tilde d}}(n)}{n}\Big| &\leq \sum_{\substack{ d\leq \Delta^2 \\ d\equiv 1 \ (\operatorname{mod}\, 8)}} \Big| \sum_{ K \leq n \leq M} \frac{\chi_{d}(n)}{n}\Big| \\ &\leq \Delta \Bigg( \sum_{\substack{ d\leq \Delta^2 \\ d\equiv 1 \ (\operatorname{mod}\, 8)}} \Big| \sum_{K \leq n \leq M} \frac{\chi_{d}(n)}{n}\Big|^2 \Bigg)^{1/2}. \end{align*}$$
Expanding the square, we obtain
 $$ \begin{align} \ \sum_{\substack{ d\leq \Delta^2 \\ d\equiv 1 \ (\operatorname{mod}\, 8)}} \Big| \sum_{ K \leq n \leq M} \frac{\chi_{d}(n)}{n}\Big|^2 = \sum_{K \leq n_1, n_2 \leq M } \frac{1}{n_1 n_2} \sum_{\substack{ d\leq \Delta^2 \\ d\equiv 1 \ (\operatorname{mod}\, 8)}} \chi_d(n_1n_2). \end{align} $$
$$ \begin{align} \ \sum_{\substack{ d\leq \Delta^2 \\ d\equiv 1 \ (\operatorname{mod}\, 8)}} \Big| \sum_{ K \leq n \leq M} \frac{\chi_{d}(n)}{n}\Big|^2 = \sum_{K \leq n_1, n_2 \leq M } \frac{1}{n_1 n_2} \sum_{\substack{ d\leq \Delta^2 \\ d\equiv 1 \ (\operatorname{mod}\, 8)}} \chi_d(n_1n_2). \end{align} $$
Write
![]() $n_1 n_2$
as
$n_1 n_2$
as
![]() $2^a n$
, where n is odd. Since
$2^a n$
, where n is odd. Since
![]() $d\equiv 1 \ (\operatorname {mod}\, 8)$
,
$d\equiv 1 \ (\operatorname {mod}\, 8)$
,
![]() $\chi _d(2)=1$
, and therefore
$\chi _d(2)=1$
, and therefore
![]() $\chi _d(n_1 n_2) = \chi _d(n)$
may also be expressed as the Jacobi symbol
$\chi _d(n_1 n_2) = \chi _d(n)$
may also be expressed as the Jacobi symbol
![]() $(\frac {d}{n})$
. Now, the Jacobi symbol
$(\frac {d}{n})$
. Now, the Jacobi symbol
![]() $( \frac {\cdot }{n})$
is a quadratic character
$( \frac {\cdot }{n})$
is a quadratic character
![]() $(\operatorname {mod}\, n)$
and is nonprincipal exactly when n is not a square, or, in other words, when
$(\operatorname {mod}\, n)$
and is nonprincipal exactly when n is not a square, or, in other words, when
![]() $n_1 n_2$
is neither a square nor twice a square. Thus, when
$n_1 n_2$
is neither a square nor twice a square. Thus, when
![]() $n_1 n_2$
is neither a square nor twice a square we find by the Pólya–Vinogradov inequality
$n_1 n_2$
is neither a square nor twice a square we find by the Pólya–Vinogradov inequality
 $$ \begin{align*}\sum_{\substack{ d\leq \Delta^2 \\ d\equiv 1 \ (\operatorname{mod}\, 8)}} \Big( \frac{d}{n}\Big) = \sum_{8k+1 \leq \Delta^2} \Big(\frac{8k+1}{n}\Big) = \Big( \frac{8}{n}\Big) \sum_{k \leq (\Delta^2-1)/8} \Big(\frac{k+\overline{8}}{n}\Big) \ll \sqrt{n} \log n, \end{align*} $$
$$ \begin{align*}\sum_{\substack{ d\leq \Delta^2 \\ d\equiv 1 \ (\operatorname{mod}\, 8)}} \Big( \frac{d}{n}\Big) = \sum_{8k+1 \leq \Delta^2} \Big(\frac{8k+1}{n}\Big) = \Big( \frac{8}{n}\Big) \sum_{k \leq (\Delta^2-1)/8} \Big(\frac{k+\overline{8}}{n}\Big) \ll \sqrt{n} \log n, \end{align*} $$
where
![]() $\overline 8$
denotes the inverse of
$\overline 8$
denotes the inverse of
![]() $8$
modulo n. If
$8$
modulo n. If
![]() $n_1 n_2$
is a square or twice a square, then the inner sum over d in (7.2) is clearly
$n_1 n_2$
is a square or twice a square, then the inner sum over d in (7.2) is clearly
![]() $O(\Delta ^2)$
. Thus, we obtain that the quantity in (7.2) is
$O(\Delta ^2)$
. Thus, we obtain that the quantity in (7.2) is
 $$ \begin{align*}\ll \Delta^2 \sum_{\substack{ K \leq n_1, n_2 \leq M \\ n_1 n_2 = \square, 2 \square}} \frac{1}{n_1 n_2} + \sum_{K \leq n_1, n_2 \leq M } \frac{\sqrt{n_1 n_2} \log (n_1n_2)}{n_1 n_2}. \end{align*} $$
$$ \begin{align*}\ll \Delta^2 \sum_{\substack{ K \leq n_1, n_2 \leq M \\ n_1 n_2 = \square, 2 \square}} \frac{1}{n_1 n_2} + \sum_{K \leq n_1, n_2 \leq M } \frac{\sqrt{n_1 n_2} \log (n_1n_2)}{n_1 n_2}. \end{align*} $$
The second term above is easily bounded by
![]() $\ll M\log M$
. Now, consider the first term, where we handle the case
$\ll M\log M$
. Now, consider the first term, where we handle the case
![]() $n_1 n_2 =m^2$
with the case
$n_1 n_2 =m^2$
with the case
![]() $n_1 n_2 =2m^2$
treated in the same manner. The terms
$n_1 n_2 =2m^2$
treated in the same manner. The terms
![]() $n_1 n_2 =m^2$
contribute, with
$n_1 n_2 =m^2$
contribute, with
![]() $\tau (\cdot )$
denoting the divisor function
$\tau (\cdot )$
denoting the divisor function
 $$ \begin{align*}\leq \Delta^2 \sum_{K \leq m \leq M} \frac{\tau(m^2)}{m^2} \leq \frac{\Delta^2}{K} \sum_{m\leq M} \frac{\tau(m^2)}{m} \ll \frac{\Delta^2}{K} \prod_{p\leq M}\Big(\sum_{j=0}^{\infty} \frac{\tau(p^{2j})}{p^j} \Big) \ll \frac{\Delta^2}{K} (\log M)^3. \end{align*} $$
$$ \begin{align*}\leq \Delta^2 \sum_{K \leq m \leq M} \frac{\tau(m^2)}{m^2} \leq \frac{\Delta^2}{K} \sum_{m\leq M} \frac{\tau(m^2)}{m} \ll \frac{\Delta^2}{K} \prod_{p\leq M}\Big(\sum_{j=0}^{\infty} \frac{\tau(p^{2j})}{p^j} \Big) \ll \frac{\Delta^2}{K} (\log M)^3. \end{align*} $$
We conclude that the quantity in (7.2) is
Combining the above argument with (7.1), we find that
 $$ \begin{align} \sum_{\substack{ d \neq \tilde{d} \in {\mathcal D}_j \\ d\equiv {\tilde d} \ (\operatorname{mod}\, 8)} } L(1,\chi_{d{\tilde d}}) = \sum_{\substack{ d \neq \tilde{d} \in {\mathcal D}_j \\ d\equiv {\tilde d} \ (\operatorname{mod}\, 8)} } \sum_{n\le K } \frac{\chi_{d {\tilde d}}(n)}{n} +O\big( \Delta^2 (\log \Delta)^{-5} \big). \end{align} $$
$$ \begin{align} \sum_{\substack{ d \neq \tilde{d} \in {\mathcal D}_j \\ d\equiv {\tilde d} \ (\operatorname{mod}\, 8)} } L(1,\chi_{d{\tilde d}}) = \sum_{\substack{ d \neq \tilde{d} \in {\mathcal D}_j \\ d\equiv {\tilde d} \ (\operatorname{mod}\, 8)} } \sum_{n\le K } \frac{\chi_{d {\tilde d}}(n)}{n} +O\big( \Delta^2 (\log \Delta)^{-5} \big). \end{align} $$
To analyse the main term above, write
![]() $n\leq K$
uniquely as
$n\leq K$
uniquely as
![]() $n= frm^2$
, where f and r are square-free with all prime factors of f being below W and all prime factors of r being above W (in particular, r is odd, and note that r could be
$n= frm^2$
, where f and r are square-free with all prime factors of f being below W and all prime factors of r being above W (in particular, r is odd, and note that r could be
![]() $1$
). Note that for all p,
$1$
). Note that for all p,
![]() $3\leq p\leq W$
, we have
$3\leq p\leq W$
, we have
![]() $\chi _{d{\widetilde d}}(p) = \chi _{D}(p) \chi _{\widetilde D}(p) =1$
. Since
$\chi _{d{\widetilde d}}(p) = \chi _{D}(p) \chi _{\widetilde D}(p) =1$
. Since
![]() $d \equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
, we have
$d \equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
, we have
![]() $d{\widetilde d} \equiv 1 \ (\operatorname {mod}\, 8)$
, and it follows also that
$d{\widetilde d} \equiv 1 \ (\operatorname {mod}\, 8)$
, and it follows also that
![]() $\chi _{d{\widetilde d}} (2) =1$
. Finally, since d and
$\chi _{d{\widetilde d}} (2) =1$
. Finally, since d and
![]() $\widetilde d$
are primes in the range
$\widetilde d$
are primes in the range
![]() $[\Delta /\log \Delta , \Delta ]$
, and
$[\Delta /\log \Delta , \Delta ]$
, and
![]() $m^2 \leq n \leq K = (\log \Delta )^{20}$
we know that
$m^2 \leq n \leq K = (\log \Delta )^{20}$
we know that
![]() $(d{\widetilde d},m^2)=1$
and therefore
$(d{\widetilde d},m^2)=1$
and therefore
![]() $\chi _{d{\widetilde d}}(m^2) =1$
. Thus,
$\chi _{d{\widetilde d}}(m^2) =1$
. Thus,
![]() $\chi _{d{\widetilde d}}(n)$
equals the Jacobi symbol
$\chi _{d{\widetilde d}}(n)$
equals the Jacobi symbol
![]() $(\frac {d{\widetilde d}}{r})$
, which for given r is a quadratic character that is principal when
$(\frac {d{\widetilde d}}{r})$
, which for given r is a quadratic character that is principal when
![]() $r=1$
and nonprincipal for
$r=1$
and nonprincipal for
![]() $r>1$
. With this notation, the main term in (7.3) may be expressed as
$r>1$
. With this notation, the main term in (7.3) may be expressed as
 $$ \begin{align} \sum_{n=fr m^2 \leq K} \frac{1}{n} \sum_{\substack{ d \neq \tilde{d} \in {\mathcal D}_j \\ d\equiv {\tilde d} \ (\operatorname{mod}\, 8)} } \Big( \frac{d{\widetilde d}}{r} \Big). \end{align} $$
$$ \begin{align} \sum_{n=fr m^2 \leq K} \frac{1}{n} \sum_{\substack{ d \neq \tilde{d} \in {\mathcal D}_j \\ d\equiv {\tilde d} \ (\operatorname{mod}\, 8)} } \Big( \frac{d{\widetilde d}}{r} \Big). \end{align} $$
We now show that the asymptotic in Proposition 5.5 arises from the contribution of
![]() $r=1$
here, while the terms with
$r=1$
here, while the terms with
![]() $r>1$
contribute a negligible amount. When
$r>1$
contribute a negligible amount. When
![]() $r=1$
, note that
$r=1$
, note that
![]() $(\frac {d \widetilde d}{r}) =1$
. Since d and
$(\frac {d \widetilde d}{r}) =1$
. Since d and
![]() ${\widetilde d}$
range over primes in
${\widetilde d}$
range over primes in
![]() $[\Delta /\log \Delta , \Delta ]$
in suitable progressions modulo
$[\Delta /\log \Delta , \Delta ]$
in suitable progressions modulo
![]() $8\prod _{3\leq p\leq W} p$
, and this modulus is
$8\prod _{3\leq p\leq W} p$
, and this modulus is
![]() $\leq e^{(1+o(1))W} = (\log \Delta )^{1+o(1)}$
, by the prime number theorem in arithmetic progressions it follows that
$\leq e^{(1+o(1))W} = (\log \Delta )^{1+o(1)}$
, by the prime number theorem in arithmetic progressions it follows that
 $$ \begin{align*}\sum_{\substack{ d \neq \tilde{d} \in {\mathcal D}_j \\ d\equiv {\tilde d} \ (\operatorname{mod}\, 8)} }1 = 2^{-j} |{\mathcal D}_j|^2 +O(\Delta^2 (\log \Delta)^{-10}). \end{align*} $$
$$ \begin{align*}\sum_{\substack{ d \neq \tilde{d} \in {\mathcal D}_j \\ d\equiv {\tilde d} \ (\operatorname{mod}\, 8)} }1 = 2^{-j} |{\mathcal D}_j|^2 +O(\Delta^2 (\log \Delta)^{-10}). \end{align*} $$
When
![]() $j=0$
the condition
$j=0$
the condition
![]() $d \equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
is automatic, while when
$d \equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
is automatic, while when
![]() $j=1$
we only know from the definition that
$j=1$
we only know from the definition that
![]() $d \equiv {\widetilde d} \ (\operatorname {mod}\, 4)$
and the extra constraint
$d \equiv {\widetilde d} \ (\operatorname {mod}\, 4)$
and the extra constraint
![]() $(\operatorname {mod}\, 8)$
accounts for the factor
$(\operatorname {mod}\, 8)$
accounts for the factor
![]() $2^j=2$
above. Now, the unrestricted sum over n satisfies
$2^j=2$
above. Now, the unrestricted sum over n satisfies
 $$ \begin{align*}\sum_{n=fm^2 \ge 1} \frac{1}{n} =\prod_{p\leq W} \big(1- p^{-1}\big)^{-1} \prod_{p>W} \big( 1- p^{-2}\big)^{-1} = \gamma_W^{-1} \big( 1+ O(W^{-1})\big), \end{align*} $$
$$ \begin{align*}\sum_{n=fm^2 \ge 1} \frac{1}{n} =\prod_{p\leq W} \big(1- p^{-1}\big)^{-1} \prod_{p>W} \big( 1- p^{-2}\big)^{-1} = \gamma_W^{-1} \big( 1+ O(W^{-1})\big), \end{align*} $$
while the tail
![]() $\sum _{n= fm^2>K} 1/n$
may be bounded by
$\sum _{n= fm^2>K} 1/n$
may be bounded by
 $$ \begin{align*}\sum_{f|\prod_{p\leq W} p} \frac 1f \sum_{m \geq \sqrt{K/f}} \frac 1{m^2} \ll \frac{1}{\sqrt{K}} \sum_{f|\prod_{p\leq W} p} \frac{1}{\sqrt{f}} \ll \frac{\log \log N}{\sqrt{K}} \ll (\log \Delta)^{-9}. \end{align*} $$
$$ \begin{align*}\sum_{f|\prod_{p\leq W} p} \frac 1f \sum_{m \geq \sqrt{K/f}} \frac 1{m^2} \ll \frac{1}{\sqrt{K}} \sum_{f|\prod_{p\leq W} p} \frac{1}{\sqrt{f}} \ll \frac{\log \log N}{\sqrt{K}} \ll (\log \Delta)^{-9}. \end{align*} $$
We conclude that the terms with
![]() $r=1$
in (7.4) contribute
$r=1$
in (7.4) contribute
This is
![]() $2^{-j} |\mathcal {D}_j|^2 \gamma _W^{-1} ( 1+ O(W^{-1}))$
, matching the expression in the proposition.
$2^{-j} |\mathcal {D}_j|^2 \gamma _W^{-1} ( 1+ O(W^{-1}))$
, matching the expression in the proposition.
It remains to show that the contribution to (7.4) of terms with
![]() $r>1$
is negligible. Given
$r>1$
is negligible. Given
![]() $d\in {\mathcal D}_j$
, consider the sum over
$d\in {\mathcal D}_j$
, consider the sum over
![]() ${\widetilde d}$
in (7.4), which is
${\widetilde d}$
in (7.4), which is
 $$ \begin{align*}\sum_{\substack {\widetilde d \in {\mathcal D}_j \\ {\widetilde d}\neq d \\ {\widetilde d}\equiv d \ (\operatorname{mod}\, 8)}} \Big( \frac{d{\widetilde d}}{r} \Big) = \Big( \frac{d}{r} \Big) \sum_{\substack {\widetilde d \in {\mathcal D}_j \\ {\widetilde d}\equiv d \ (\operatorname{mod}\, 8)}} \Big( \frac{{\widetilde d}}{r} \Big) + O(1) =\Big( \frac{d}{r} \Big) \sum_{ a\ (\operatorname{mod}\, r)} \Big( \frac{a}{r} \Big) \sum_{\substack {\widetilde d \in {\mathcal D}_j \\ {\widetilde d}\equiv d \ (\operatorname{mod}\, 8)\\ d\equiv a \ (\operatorname{mod}\, r)}} \!\!\!\! 1 +O(1). \end{align*} $$
$$ \begin{align*}\sum_{\substack {\widetilde d \in {\mathcal D}_j \\ {\widetilde d}\neq d \\ {\widetilde d}\equiv d \ (\operatorname{mod}\, 8)}} \Big( \frac{d{\widetilde d}}{r} \Big) = \Big( \frac{d}{r} \Big) \sum_{\substack {\widetilde d \in {\mathcal D}_j \\ {\widetilde d}\equiv d \ (\operatorname{mod}\, 8)}} \Big( \frac{{\widetilde d}}{r} \Big) + O(1) =\Big( \frac{d}{r} \Big) \sum_{ a\ (\operatorname{mod}\, r)} \Big( \frac{a}{r} \Big) \sum_{\substack {\widetilde d \in {\mathcal D}_j \\ {\widetilde d}\equiv d \ (\operatorname{mod}\, 8)\\ d\equiv a \ (\operatorname{mod}\, r)}} \!\!\!\! 1 +O(1). \end{align*} $$
Now, the sum over
![]() ${\widetilde d}$
above counts primes in
${\widetilde d}$
above counts primes in
![]() $[\Delta /\log \Delta ,\Delta ]$
lying in a suitable number of arithmetic progressions modulo
$[\Delta /\log \Delta ,\Delta ]$
lying in a suitable number of arithmetic progressions modulo
![]() $8r \prod _{3\leq p\leq W} p$
. Since the modulus is
$8r \prod _{3\leq p\leq W} p$
. Since the modulus is
![]() $\ll K e^{(1+o(1))W} \leq (\log \Delta )^{22}$
, an application of the prime number theorem in arithmetic progressions shows that the above equals
$\ll K e^{(1+o(1))W} \leq (\log \Delta )^{22}$
, an application of the prime number theorem in arithmetic progressions shows that the above equals
 $$ \begin{align*}\Big( \frac{d}{r} \Big) \sum_{ a\ (\operatorname{mod}\, r)} \Big( \frac{a}{r} \Big) \Big( \frac{1}{\phi(r)} \frac{|{\mathcal D}_j|}{2^j} + O\big(\Delta(\log \Delta)^{-40}\big) \Big) = O\big( \Delta (\log \Delta)^{-20}\big), \end{align*} $$
$$ \begin{align*}\Big( \frac{d}{r} \Big) \sum_{ a\ (\operatorname{mod}\, r)} \Big( \frac{a}{r} \Big) \Big( \frac{1}{\phi(r)} \frac{|{\mathcal D}_j|}{2^j} + O\big(\Delta(\log \Delta)^{-40}\big) \Big) = O\big( \Delta (\log \Delta)^{-20}\big), \end{align*} $$
upon noting that the main terms cancel (since
![]() $(\frac {\cdot }{r})$
is a nonprincipal character) and that
$(\frac {\cdot }{r})$
is a nonprincipal character) and that
![]() $r\leq K = (\log \Delta )^{20}$
. Thus, the contribution of the terms
$r\leq K = (\log \Delta )^{20}$
. Thus, the contribution of the terms
![]() $r>1$
to (7.4) is
$r>1$
to (7.4) is
 $$ \begin{align*}\ll \sum_{n \leq K} \frac{1}{n} |{\mathcal D}_j| \Delta (\log \Delta)^{-20} \ll \Delta^2(\log \Delta)^{-19}. \end{align*} $$
$$ \begin{align*}\ll \sum_{n \leq K} \frac{1}{n} |{\mathcal D}_j| \Delta (\log \Delta)^{-20} \ll \Delta^2(\log \Delta)^{-19}. \end{align*} $$
Combining this with our evaluation of the terms with
![]() $r=1$
, we conclude that the quantity in (7.4) is
$r=1$
, we conclude that the quantity in (7.4) is
![]() $2^{-j} \gamma _W^{-1} |{\mathcal D}_j|^2 (1+O(W^{-1}))$
, and using this in (7.3) the proof of Proposition 5.5 is complete.
$2^{-j} \gamma _W^{-1} |{\mathcal D}_j|^2 (1+O(W^{-1}))$
, and using this in (7.3) the proof of Proposition 5.5 is complete.
8 Class group L-functions
We begin by recalling properties of class group L-functions over general number fields. In our work, we will only need the special cases of quadratic and biquadratic extensions. Let K be a number field of degree m and discriminant
![]() $D_K$
. Let
$D_K$
. Let
![]() $\Psi $
be a character of the class group of K, and let
$\Psi $
be a character of the class group of K, and let
![]() $L(s,\Psi )$
denote the corresponding L-function. Recall that
$L(s,\Psi )$
denote the corresponding L-function. Recall that
![]() $L(s,\Psi )$
is defined by
$L(s,\Psi )$
is defined by
 $$ \begin{align} L(s, \Psi) = \sum_{\mathfrak a \neq 0} \Psi(\mathfrak a) N(\mathfrak a)^{-s} = \prod_{\mathfrak p} \big(1 - \Psi(\mathfrak p) N(\mathfrak p)^{-s} \big)^{-1}, \end{align} $$
$$ \begin{align} L(s, \Psi) = \sum_{\mathfrak a \neq 0} \Psi(\mathfrak a) N(\mathfrak a)^{-s} = \prod_{\mathfrak p} \big(1 - \Psi(\mathfrak p) N(\mathfrak p)^{-s} \big)^{-1}, \end{align} $$
where both the Dirichlet series and Euler product above converge absolutely in the half-plane
![]() $\sigma> 1$
. In the half-plane
$\sigma> 1$
. In the half-plane
![]() $\sigma>1$
, we define a holomorphic branch of
$\sigma>1$
, we define a holomorphic branch of
![]() $\log L(s,\Psi )$
by setting
$\log L(s,\Psi )$
by setting
 $$ \begin{align} \log L(s,\Psi) = \sum_{\mathfrak p} \log \big( 1- \Psi(\mathfrak p) N(\mathfrak p)^{-s}\big)^{-1} = \sum_{\mathfrak p} \sum_{j=1}^{\infty} \frac{1}{j} \Psi(\mathfrak p)^j N(\mathfrak p)^{-js}. \end{align} $$
$$ \begin{align} \log L(s,\Psi) = \sum_{\mathfrak p} \log \big( 1- \Psi(\mathfrak p) N(\mathfrak p)^{-s}\big)^{-1} = \sum_{\mathfrak p} \sum_{j=1}^{\infty} \frac{1}{j} \Psi(\mathfrak p)^j N(\mathfrak p)^{-js}. \end{align} $$
The Dirichlet series coefficients of
![]() $L(s,\Psi )$
are bounded in absolute value by the corresponding coefficients of the Dedekind zeta-function
$L(s,\Psi )$
are bounded in absolute value by the corresponding coefficients of the Dedekind zeta-function
![]() $\zeta _K(s)$
, which in turn are no more than the coefficients of
$\zeta _K(s)$
, which in turn are no more than the coefficients of
![]() $\zeta (s)^m$
(which has coefficients given by the m-divisor function). Further, the coefficients of
$\zeta (s)^m$
(which has coefficients given by the m-divisor function). Further, the coefficients of
![]() $\log L(s,\Psi )$
(as defined above) are supported on prime powers and bounded in size by the coefficients of
$\log L(s,\Psi )$
(as defined above) are supported on prime powers and bounded in size by the coefficients of
![]() $\log \zeta _K(s)$
(defined as above for the principal character
$\log \zeta _K(s)$
(defined as above for the principal character
![]() $\Psi _0$
) and thus are no more than
$\Psi _0$
) and thus are no more than
![]() $m/j$
on the prime powers
$m/j$
on the prime powers
![]() $p^j$
. In particular, we note that in the half-plane
$p^j$
. In particular, we note that in the half-plane
![]() $\sigma>1$
$\sigma>1$
with the second bound being a standard bound for
![]() $\zeta $
(see, for instance, [Reference Montgomery and Vaughan14, Corollary 1.4]).
$\zeta $
(see, for instance, [Reference Montgomery and Vaughan14, Corollary 1.4]).
We now collect together some classical bounds for
![]() $L(s,\Psi )$
, along with describing a zero-free region for
$L(s,\Psi )$
, along with describing a zero-free region for
![]() $L(s,\Psi )$
and bounds for
$L(s,\Psi )$
and bounds for
![]() $|\log L(s,\Psi )|$
inside the zero-free region.
$|\log L(s,\Psi )|$
inside the zero-free region.
Lemma 8.1. Let K,
![]() $\Psi $
and
$\Psi $
and
![]() $L(s,\Psi )$
be as above. Then the following statements hold.
$L(s,\Psi )$
be as above. Then the following statements hold.
-
1. Suppose that
 $\Psi $
is not the principal character. Then
$\Psi $
is not the principal character. Then
 $L(s,\Psi )$
extends to an entire function and uniformly in the region
$L(s,\Psi )$
extends to an entire function and uniformly in the region
 $\sigma \geq 0$
satisfies the bound (8.4)
$\sigma \geq 0$
satisfies the bound (8.4) $$ \begin{align} |L(\sigma+it,\Psi)| \ll_m \Big( (|D_K| (1+|t|)^m)^{(1-\sigma)/2} + 1 \Big) (\log (|D_K|(1+|t|)))^{m}. \end{align} $$
$$ \begin{align} |L(\sigma+it,\Psi)| \ll_m \Big( (|D_K| (1+|t|)^m)^{(1-\sigma)/2} + 1 \Big) (\log (|D_K|(1+|t|)))^{m}. \end{align} $$
For every
 $\varepsilon>0$
, there is a constant
$\varepsilon>0$
, there is a constant
 $C=C(m,\varepsilon )>0$
such that the region is free of zeros of
$C=C(m,\varepsilon )>0$
such that the region is free of zeros of $$\begin{align*}{\mathcal R}_0 = {\mathcal R}_0(\varepsilon) = \{ \sigma \geq 1- C |D_K|^{-\varepsilon}, \ \ |t| \leq |D_K| \} \end{align*}$$
$$\begin{align*}{\mathcal R}_0 = {\mathcal R}_0(\varepsilon) = \{ \sigma \geq 1- C |D_K|^{-\varepsilon}, \ \ |t| \leq |D_K| \} \end{align*}$$
 $L(s,\Psi )$
. Thus,
$L(s,\Psi )$
. Thus,
 $\log L(s,\Psi )$
extends analytically to the region
$\log L(s,\Psi )$
extends analytically to the region
 ${\mathcal R}_0$
, and moreover in the subregion we have the bound
${\mathcal R}_0$
, and moreover in the subregion we have the bound $$\begin{align*}{\mathcal R} = {\mathcal R}(\varepsilon) = \Big \{ \sigma \geq 1- \tfrac{1}{2} C |D_K|^{-\varepsilon}, \ \ |t| \leq \tfrac{1}{2} |D_K| \Big\}, \end{align*}$$
(8.5)
$$\begin{align*}{\mathcal R} = {\mathcal R}(\varepsilon) = \Big \{ \sigma \geq 1- \tfrac{1}{2} C |D_K|^{-\varepsilon}, \ \ |t| \leq \tfrac{1}{2} |D_K| \Big\}, \end{align*}$$
(8.5) $$ \begin{align} |\log L(s,\Psi)| \leq 6m\varepsilon \log |D_K| + O_{m,\varepsilon}(1). \end{align} $$
$$ \begin{align} |\log L(s,\Psi)| \leq 6m\varepsilon \log |D_K| + O_{m,\varepsilon}(1). \end{align} $$
-
2. Suppose that
 $\Psi $
is the principal character so that
$\Psi $
is the principal character so that
 $L(s,\Psi )$
is the Dedekind zeta-function
$L(s,\Psi )$
is the Dedekind zeta-function
 $\zeta _K(s)$
of the field K. The Dedekind zeta-function extends to a meromorphic function, with a single simple pole at
$\zeta _K(s)$
of the field K. The Dedekind zeta-function extends to a meromorphic function, with a single simple pole at
 $s=1$
. The convexity bound (8.4) holds provided
$s=1$
. The convexity bound (8.4) holds provided
 $|t| \geq 1$
, while for
$|t| \geq 1$
, while for
 $|t|\leq 1$
the same bound holds for
$|t|\leq 1$
the same bound holds for
 $|(s-1)\zeta _K(s)|$
. The region
$|(s-1)\zeta _K(s)|$
. The region
 ${\mathcal R}_0$
is free of zeros of
${\mathcal R}_0$
is free of zeros of
 $\zeta _K(s)$
, and the function
$\zeta _K(s)$
, and the function
 $\log ((s-1)\zeta _K(s))$
extends analytically to the region
$\log ((s-1)\zeta _K(s))$
extends analytically to the region
 ${\mathcal R}_0$
. The bound (8.5) holds for
${\mathcal R}_0$
. The bound (8.5) holds for
 $|\log \zeta (s)|$
in the subregion
$|\log \zeta (s)|$
in the subregion
 ${\mathcal R}$
provided
${\mathcal R}$
provided
 $|s-1| \geq 1$
, and for points in
$|s-1| \geq 1$
, and for points in
 ${\mathcal R}$
with
${\mathcal R}$
with
 $|s-1| \leq 1$
the same bound holds for
$|s-1| \leq 1$
the same bound holds for
 $|\log ((s-1) \zeta _K(s))|$
instead.
$|\log ((s-1) \zeta _K(s))|$
instead.
Proof. Suppose first that
![]() $\Psi $
is nonprincipal. The analytic continuation of
$\Psi $
is nonprincipal. The analytic continuation of
![]() $L(s,\Psi )$
to the entire plane is due to Hecke (for a modern account, see, for example, Chapter 7 of [Reference Narkiewicz15]).
$L(s,\Psi )$
to the entire plane is due to Hecke (for a modern account, see, for example, Chapter 7 of [Reference Narkiewicz15]).
The bound in (8.4) is a standard convexity bound and, for instance, may be obtained from Lemma 4 of Fogels [Reference Fogels8]. Fogels’s paper [Reference Fogels8] established a classical zero-free region for
![]() $L(s,\Psi )$
of the form
$L(s,\Psi )$
of the form
![]() $\sigma \geq 1- c/\log (|D|(1+|t|))$
for a suitable constant
$\sigma \geq 1- c/\log (|D|(1+|t|))$
for a suitable constant
![]() $c>0$
, when the character
$c>0$
, when the character
![]() $\Psi $
is complex. In the case of a real character
$\Psi $
is complex. In the case of a real character
![]() $\Psi $
, the same region is free of zeros of
$\Psi $
, the same region is free of zeros of
![]() $L(s,\Psi )$
except for the possibility of a simple zero at
$L(s,\Psi )$
except for the possibility of a simple zero at
![]() $1-\delta $
for a real number
$1-\delta $
for a real number
![]() $\delta $
(analogous to the Siegel zero for Dirichlet L-functions). Analogously to the Brauer–Siegel theorem, Fogels [Reference Fogels9] shows, by reducing to Brauer’s work, that
$\delta $
(analogous to the Siegel zero for Dirichlet L-functions). Analogously to the Brauer–Siegel theorem, Fogels [Reference Fogels9] shows, by reducing to Brauer’s work, that
![]() $\delta \geq C(m, \varepsilon ) |D_K|^{-\varepsilon }$
. Thus, the region
$\delta \geq C(m, \varepsilon ) |D_K|^{-\varepsilon }$
. Thus, the region
![]() ${\mathcal R}_0$
is free of zeros of
${\mathcal R}_0$
is free of zeros of
![]() $L(s,\Psi )$
.
$L(s,\Psi )$
.
The bound (8.5) on
![]() $|\log L(s,\Psi )|$
in the narrower region
$|\log L(s,\Psi )|$
in the narrower region
![]() ${\mathcal R}$
follows by an application of the Borel–Caratheodory lemma using the preliminary bounds (8.3) and (8.4), as we shall now see. Let
${\mathcal R}$
follows by an application of the Borel–Caratheodory lemma using the preliminary bounds (8.3) and (8.4), as we shall now see. Let
![]() $z_0 = 1+ \frac C2 |D_K|^{-\varepsilon } +i t$
with
$z_0 = 1+ \frac C2 |D_K|^{-\varepsilon } +i t$
with
![]() $|t|\leq |D_K|/2$
, and put
$|t|\leq |D_K|/2$
, and put
![]() $r= C|D_K|^{-\varepsilon }$
and
$r= C|D_K|^{-\varepsilon }$
and
![]() $R = \frac 32 C |D_K|^{-\varepsilon }$
. The function
$R = \frac 32 C |D_K|^{-\varepsilon }$
. The function
![]() $f(z) = \log L(z,\Psi )$
is holomorphic inside the circle of radius R centered at
$f(z) = \log L(z,\Psi )$
is holomorphic inside the circle of radius R centered at
![]() $z_0$
(since this is contained in the region
$z_0$
(since this is contained in the region
![]() ${\mathcal R}_0$
), and for z inside this larger circle it satisfies the bound
${\mathcal R}_0$
), and for z inside this larger circle it satisfies the bound
since by (8.4) we have
![]() $|L(z,\Psi )| \ll _{m,\epsilon } (\log |D_K|)^m$
. Further, by (8.3)
$|L(z,\Psi )| \ll _{m,\epsilon } (\log |D_K|)^m$
. Further, by (8.3)
The Borel–Carathéodory lemma (see, for example, Section 5.5 of [Reference Titchmarsh18]) now shows that for z inside the smaller circle
![]() $|z-z_0| \leq r$
one has
$|z-z_0| \leq r$
one has
 $$ \begin{align*} |f(z)| &\leq \frac{2r}{R-r} \sup_{|z-z_0| \leq R}{\operatorname{Re}} f(z) + \frac{R+r}{R-r} |f(z_0)| \\ &\leq 4 m \log \log |D_K| + 5m \varepsilon \log |D_K| + O_{m,\varepsilon}(1) \le 6m \varepsilon \log |D_K| + O_{m,\varepsilon}(1). \end{align*} $$
$$ \begin{align*} |f(z)| &\leq \frac{2r}{R-r} \sup_{|z-z_0| \leq R}{\operatorname{Re}} f(z) + \frac{R+r}{R-r} |f(z_0)| \\ &\leq 4 m \log \log |D_K| + 5m \varepsilon \log |D_K| + O_{m,\varepsilon}(1) \le 6m \varepsilon \log |D_K| + O_{m,\varepsilon}(1). \end{align*} $$
This establishes (8.5) for all
![]() $s= \sigma +it$
with
$s= \sigma +it$
with
![]() $|t|\leq \frac {1}{2}|D_K|$
and
$|t|\leq \frac {1}{2}|D_K|$
and
![]() $1-\frac {1}{2} C |D_K|^{\varepsilon } \leq \sigma \leq 1+ \frac {3}{2}C |D_K|^{-\varepsilon }$
. When
$1-\frac {1}{2} C |D_K|^{\varepsilon } \leq \sigma \leq 1+ \frac {3}{2}C |D_K|^{-\varepsilon }$
. When
![]() $\sigma> 1+\frac {3}{2}C |D_K|^{-\varepsilon }$
(and
$\sigma> 1+\frac {3}{2}C |D_K|^{-\varepsilon }$
(and
![]() $|t| \leq \frac {1}{2}|D_K|$
) the bound in (8.5) follows at once from (8.3), and this completes the proof in the case of nonprincipal
$|t| \leq \frac {1}{2}|D_K|$
) the bound in (8.5) follows at once from (8.3), and this completes the proof in the case of nonprincipal
![]() $\Psi $
.
$\Psi $
.
The case when
![]() $\Psi $
is principal follows in the same way. The only difference is that the Dedekind zeta-function has a pole at
$\Psi $
is principal follows in the same way. The only difference is that the Dedekind zeta-function has a pole at
![]() $s=1$
so that near
$s=1$
so that near
![]() $1$
we deal with
$1$
we deal with
![]() $(s-1) \zeta _K(s)$
instead.
$(s-1) \zeta _K(s)$
instead.
To prove Propositions 5.2, 5.3 and 5.4, we shall make use of the expression (3.4) of
![]() $R_D(n)$
in terms of the coefficients of the class group L-functions
$R_D(n)$
in terms of the coefficients of the class group L-functions
![]() $r(n,\psi )$
. As consequences of Lemma 8.1, we now show that in such expressions the contribution of most class group characters
$r(n,\psi )$
. As consequences of Lemma 8.1, we now show that in such expressions the contribution of most class group characters
![]() $\psi $
is negligible. The main lemmas we will prove in this section are Lemmas 8.2, 8.4 and 8.5. The analytic details are very similar across all three, so we will only give complete details in the proof of Lemma 8.2.
$\psi $
is negligible. The main lemmas we will prove in this section are Lemmas 8.2, 8.4 and 8.5. The analytic details are very similar across all three, so we will only give complete details in the proof of Lemma 8.2.
Recall the convention introduced in Section 5, namely that for integer n we write
![]() $n = n^{\sharp } n^{\flat }$
, where
$n = n^{\sharp } n^{\flat }$
, where
![]() $n^{\sharp }$
has only prime factors
$n^{\sharp }$
has only prime factors
![]() $\leq W$
, and
$\leq W$
, and
![]() $n^{\flat }$
only prime factors
$n^{\flat }$
only prime factors
![]() $>W$
.
$>W$
.
Lemma 8.2. Let N be large and k be an integer in the range (5.5). Let j be
![]() $0$
or
$0$
or
![]() $1$
, and let d be an element of
$1$
, and let d be an element of
![]() ${\mathcal D}_j$
with D denoting the corresponding fundamental discriminant. Let
${\mathcal D}_j$
with D denoting the corresponding fundamental discriminant. Let
![]() $\psi $
be a nonprincipal class group character of the quadratic field
$\psi $
be a nonprincipal class group character of the quadratic field
![]() $K=\mathbf {Q}(\sqrt {D})$
. Then
$K=\mathbf {Q}(\sqrt {D})$
. Then
 $$\begin{align*}\sum_{n\in {\mathcal A}_j(k)} \frac{r(n,\psi)}{\tau(n^{\flat})} e^{-n/N} \ll N(\log N)^{-100}. \end{align*}$$
$$\begin{align*}\sum_{n\in {\mathcal A}_j(k)} \frac{r(n,\psi)}{\tau(n^{\flat})} e^{-n/N} \ll N(\log N)^{-100}. \end{align*}$$
Proof. The key idea here and in the proofs of Lemmas 8.4 and 8.5 is to follow Selberg [Reference Selberg16] and introduce, for any
![]() $z \in \mathbf {C}$
with
$z \in \mathbf {C}$
with
![]() $|z| = 1$
, the Dirichlet series
$|z| = 1$
, the Dirichlet series
 $$\begin{align*}\mathcal{F}(s;z,j) := \sum_{v_2(n) = j} \frac{r(n,\psi)}{\tau(n^{\flat})} z^{\Omega(n)} n^{-s}. \end{align*}$$
$$\begin{align*}\mathcal{F}(s;z,j) := \sum_{v_2(n) = j} \frac{r(n,\psi)}{\tau(n^{\flat})} z^{\Omega(n)} n^{-s}. \end{align*}$$
Later, we will recover the condition
![]() $\Omega (n) = k$
(which defines the set
$\Omega (n) = k$
(which defines the set
![]() $\mathcal {A}_j(k)$
) by Fourier inversion.
$\mathcal {A}_j(k)$
) by Fourier inversion.
Since (by (3.2), (3.3))
![]() $|r(n,\psi )| \leq \tau (n)$
, we see that
$|r(n,\psi )| \leq \tau (n)$
, we see that
![]() ${\mathcal F}(s,z,j)$
converges absolutely in the half plane Re
${\mathcal F}(s,z,j)$
converges absolutely in the half plane Re
![]() $(s) =\sigma>1$
and further satisfies the bound
$(s) =\sigma>1$
and further satisfies the bound
 $$ \begin{align} |{\mathcal F}(s; z,j)| \leq \sum_{n=1}^{\infty} \tau(n) n^{-\sigma} = \zeta(\sigma)^2 \leq \Big( \frac{\sigma}{\sigma-1}\Big)^2, \end{align} $$
$$ \begin{align} |{\mathcal F}(s; z,j)| \leq \sum_{n=1}^{\infty} \tau(n) n^{-\sigma} = \zeta(\sigma)^2 \leq \Big( \frac{\sigma}{\sigma-1}\Big)^2, \end{align} $$
using [Reference Montgomery and Vaughan14, Corollary 1.4] in the last step. Further, by Mellin inversion we have, setting
![]() $c= 1+1/\log N$
,
$c= 1+1/\log N$
,
 $$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} \frac{r(n,\psi)}{\tau(n^{\flat})}z^{\Omega(n)} e^{-n/N} = \frac{1}{2\pi i} \int_{c-i\infty}^{c+i\infty} {\mathcal F}(s; z,j) N^s \Gamma(s) ds. \end{align} $$
$$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} \frac{r(n,\psi)}{\tau(n^{\flat})}z^{\Omega(n)} e^{-n/N} = \frac{1}{2\pi i} \int_{c-i\infty}^{c+i\infty} {\mathcal F}(s; z,j) N^s \Gamma(s) ds. \end{align} $$
By Stirling’s formula
![]() $|\Gamma (\sigma + it)| \ll (1+|t|)^{\sigma -1/2} e^{-\pi |t|/2}$
uniformly for
$|\Gamma (\sigma + it)| \ll (1+|t|)^{\sigma -1/2} e^{-\pi |t|/2}$
uniformly for
![]() $\sigma $
in bounded intervals (see, for instance, (C.19) of [Reference Montgomery and Vaughan14]). Combining this with the bound (8.6), we find that the tails of the integral in (8.7) above where
$\sigma $
in bounded intervals (see, for instance, (C.19) of [Reference Montgomery and Vaughan14]). Combining this with the bound (8.6), we find that the tails of the integral in (8.7) above where
![]() $|\text {Im}(s)| \geq (\log \log N)^2$
contribute
$|\text {Im}(s)| \geq (\log \log N)^2$
contribute
 $$\begin{align*}\ll \int_{|t|> (\log \log N)^2} N^c (\log N)^2 (1+|t|)^{c-1/2} e^{-\pi |t|/2} dt \ll N (\log N)^{-100}. \end{align*}$$
$$\begin{align*}\ll \int_{|t|> (\log \log N)^2} N^c (\log N)^2 (1+|t|)^{c-1/2} e^{-\pi |t|/2} dt \ll N (\log N)^{-100}. \end{align*}$$
Thus, writing
![]() $T= (\log \log N)^2$
,
$T= (\log \log N)^2$
,
 $$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} \frac{r(n,\psi)}{\tau(n^{\flat})} z^{\Omega(n)}e^{-n/N} = \frac{1}{2\pi i} \int_{c-iT}^{c+iT} {\mathcal F}(s; z,j) N^s \Gamma(s) ds + O\big( N (\log N)^{-100}\big). \end{align} $$
$$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} \frac{r(n,\psi)}{\tau(n^{\flat})} z^{\Omega(n)}e^{-n/N} = \frac{1}{2\pi i} \int_{c-iT}^{c+iT} {\mathcal F}(s; z,j) N^s \Gamma(s) ds + O\big( N (\log N)^{-100}\big). \end{align} $$
To estimate the truncated integral here, we shall extend
![]() ${\mathcal F}(s;z,j)$
analytically a little to the left of the
${\mathcal F}(s;z,j)$
analytically a little to the left of the
![]() $1$
-line and shift contours. To extend
$1$
-line and shift contours. To extend
![]() ${\mathcal F}(s;z,j)$
analytically, we shall compare it with
${\mathcal F}(s;z,j)$
analytically, we shall compare it with
![]() $L(s,\psi )^z$
. Note that when Re
$L(s,\psi )^z$
. Note that when Re
![]() $(s)>1$
we may define
$(s)>1$
we may define
![]() $L(s,\psi )^z$
by the Euler product
$L(s,\psi )^z$
by the Euler product
![]() $\prod _{\mathfrak p} (1- \psi (\mathfrak p)/N(\mathfrak p)^s)^{-z}$
, and this product converges absolutely when Re
$\prod _{\mathfrak p} (1- \psi (\mathfrak p)/N(\mathfrak p)^s)^{-z}$
, and this product converges absolutely when Re
![]() $(s)>1$
. Further, we may extend
$(s)>1$
. Further, we may extend
![]() $L(s,\psi )^z$
analytically to a wider region by writing it as
$L(s,\psi )^z$
analytically to a wider region by writing it as
![]() $\exp (z\log L(s,\psi ))$
and using the analytic continuation described in Lemma 8.1. Thus, define
$\exp (z\log L(s,\psi ))$
and using the analytic continuation described in Lemma 8.1. Thus, define
which is, to start with, analytic in the half-plane
![]() $\sigma>1$
. The definition of
$\sigma>1$
. The definition of
![]() ${\mathcal F}(s;z,j)$
permits us (in this region) to write
${\mathcal F}(s;z,j)$
permits us (in this region) to write
![]() ${\mathcal G}(s;z,j)$
as an Euler product
${\mathcal G}(s;z,j)$
as an Euler product
![]() $\prod _p {\mathcal G}_p(s;z,j)$
, whose factors we now describe. For
$\prod _p {\mathcal G}_p(s;z,j)$
, whose factors we now describe. For
![]() $p>W$
, we have
$p>W$
, we have
 $$ \begin{align*} {\mathcal G}_p(s;z,j) &= \Big( \sum_{j=0}^{\infty} z^j r(p^j,\psi) p^{-js} \Big) \prod_{ {\mathfrak p}|p} \big(1 -\psi(\mathfrak p)N(\mathfrak p)^{-s} \big)^z \\ &= \Big( 1+ zr(p,\psi) p^{-s} + O(p^{-2\sigma}) \Big) \big( 1 - z p^{-s} \sum_{N(\mathfrak p) =p} \psi(\mathfrak p) + O( p^{-2\sigma})\big) \\ &= 1+ O(p^{-2\sigma}). \end{align*} $$
$$ \begin{align*} {\mathcal G}_p(s;z,j) &= \Big( \sum_{j=0}^{\infty} z^j r(p^j,\psi) p^{-js} \Big) \prod_{ {\mathfrak p}|p} \big(1 -\psi(\mathfrak p)N(\mathfrak p)^{-s} \big)^z \\ &= \Big( 1+ zr(p,\psi) p^{-s} + O(p^{-2\sigma}) \Big) \big( 1 - z p^{-s} \sum_{N(\mathfrak p) =p} \psi(\mathfrak p) + O( p^{-2\sigma})\big) \\ &= 1+ O(p^{-2\sigma}). \end{align*} $$
For p with
![]() $3\leq p\leq W$
, we have
$3\leq p\leq W$
, we have
 $$\begin{align*}{\mathcal G}_p(s;z,j) = \Big( \sum_{j=0}^{\infty} \frac{r(p^j,\psi)}{(j+1)} z^j p^{-js}\Big) \prod_{ {\mathfrak p}|p} \big(1 -\psi(\mathfrak p)N(\mathfrak p)^{-s} \big)^z = 1+ O(p^{-\sigma}). \end{align*}$$
$$\begin{align*}{\mathcal G}_p(s;z,j) = \Big( \sum_{j=0}^{\infty} \frac{r(p^j,\psi)}{(j+1)} z^j p^{-js}\Big) \prod_{ {\mathfrak p}|p} \big(1 -\psi(\mathfrak p)N(\mathfrak p)^{-s} \big)^z = 1+ O(p^{-\sigma}). \end{align*}$$
Finally, for
![]() $p=2$
we have
$p=2$
we have
 $$\begin{align*}{\mathcal G}_2(s;z,j) = \left\{\begin{array}{ll} z 2^{-s-1} r(2,\psi) \prod_{\mathfrak p| 2} \big(1- \psi(\mathfrak p)N(\mathfrak p)^{-s}\big)^{z} &\text{ if } j=1 \\ \prod_{\mathfrak p| 2} \big(1- \psi(\mathfrak p) N(\mathfrak p)^{-s}\big)^{z} &\text{ if } j =0, \end{array}\right. \end{align*}$$
$$\begin{align*}{\mathcal G}_2(s;z,j) = \left\{\begin{array}{ll} z 2^{-s-1} r(2,\psi) \prod_{\mathfrak p| 2} \big(1- \psi(\mathfrak p)N(\mathfrak p)^{-s}\big)^{z} &\text{ if } j=1 \\ \prod_{\mathfrak p| 2} \big(1- \psi(\mathfrak p) N(\mathfrak p)^{-s}\big)^{z} &\text{ if } j =0, \end{array}\right. \end{align*}$$
and in both cases this is
![]() $1+O(2^{-\sigma })$
. From these remarks, we see that the Euler product
$1+O(2^{-\sigma })$
. From these remarks, we see that the Euler product
![]() ${\mathcal G}_p(s;z,j)$
converges absolutely in the region
${\mathcal G}_p(s;z,j)$
converges absolutely in the region
![]() ${\operatorname {Re}}(s)>\frac {1}{2}$
and defines a holomorphic function of s in that region. Moreover, in the region
${\operatorname {Re}}(s)>\frac {1}{2}$
and defines a holomorphic function of s in that region. Moreover, in the region
![]() $\sigma \geq \frac {3}{4}$
, we have the bound
$\sigma \geq \frac {3}{4}$
, we have the bound
For the rest of the paper, we fix the domain
Applying Lemma 8.1 with
![]() $\varepsilon =\frac {1}{100}$
(and
$\varepsilon =\frac {1}{100}$
(and
![]() $m=2$
), we see that (keeping in mind
$m=2$
), we see that (keeping in mind
![]() $(\log N)^{1/2} \leq |D| \leq \log N$
) the function
$(\log N)^{1/2} \leq |D| \leq \log N$
) the function
![]() $\log L(s,\psi )$
is analytic in
$\log L(s,\psi )$
is analytic in
![]() $\mathcal {W}$
and satisfies
$\mathcal {W}$
and satisfies
![]() $|\log L(s,\psi )| \leq \frac 18 \log |D| +O(1)$
here. Therefore,
$|\log L(s,\psi )| \leq \frac 18 \log |D| +O(1)$
here. Therefore,
is also analytic in
![]() $\mathcal {W}$
and by (8.9) satisfies in this region
$\mathcal {W}$
and by (8.9) satisfies in this region
We now return to the integral in (8.8), and replace the line of integration from
![]() $c-iT$
to
$c-iT$
to
![]() $c+iT$
by integrals along the following three line segments: (i) the horizontal line segment from
$c+iT$
by integrals along the following three line segments: (i) the horizontal line segment from
![]() $c-iT$
to
$c-iT$
to
![]() $1-(\log N)^{-1/2} -iT$
, (ii) the vertical line segment from
$1-(\log N)^{-1/2} -iT$
, (ii) the vertical line segment from
![]() $1-(\log N)^{-1/2} -iT$
to
$1-(\log N)^{-1/2} -iT$
to
![]() $1-(\log N)^{-1/2} +iT$
and (iii) the horizontal line segment from
$1-(\log N)^{-1/2} +iT$
and (iii) the horizontal line segment from
![]() $1-(\log N)^{-1/2} +iT$
to
$1-(\log N)^{-1/2} +iT$
to
![]() $c+iT$
. On the horizontal line segment (i), we may bound the integral by
$c+iT$
. On the horizontal line segment (i), we may bound the integral by
 $$ \begin{align*}\ll \int_{1-(\log N)^{-1/2}}^{c} N^{\sigma} (\log N) |\Gamma(\sigma -iT)| d\sigma \ll N (\log N) e^{-T} \ll N(\log N)^{-100}, \end{align*} $$
$$ \begin{align*}\ll \int_{1-(\log N)^{-1/2}}^{c} N^{\sigma} (\log N) |\Gamma(\sigma -iT)| d\sigma \ll N (\log N) e^{-T} \ll N(\log N)^{-100}, \end{align*} $$
upon using
![]() $|\Gamma (\sigma -iT)| \ll T^{\sigma -1/2} e^{-\pi T/2} \ll e^{-T}$
. Naturally, the same estimate applies to the integral on the horizontal line segment in (iii). As for the vertical line segment (ii), the integral here is
$|\Gamma (\sigma -iT)| \ll T^{\sigma -1/2} e^{-\pi T/2} \ll e^{-T}$
. Naturally, the same estimate applies to the integral on the horizontal line segment in (iii). As for the vertical line segment (ii), the integral here is
 $$ \begin{align*} &\ll N^{1- (\log N)^{-1/2}} (\log N) \int_{-T}^{T} |\Gamma( 1-(\log N)^{-1/2} +it)| dt \\ &\ll N (\log N) \exp(-\sqrt{\log N}) \ll N(\log N)^{-100}. \end{align*} $$
$$ \begin{align*} &\ll N^{1- (\log N)^{-1/2}} (\log N) \int_{-T}^{T} |\Gamma( 1-(\log N)^{-1/2} +it)| dt \\ &\ll N (\log N) \exp(-\sqrt{\log N}) \ll N(\log N)^{-100}. \end{align*} $$
Putting all this together and recalling (8.1), we conclude that uniformly for
![]() $|z|=1$
$|z|=1$
 $$\begin{align*}\sum_{v_2(n) = j} \frac{r(n,\psi)}{\tau(n^{\flat})} z^{\Omega(n)} e^{-n/N} \ll N(\log N)^{-100}. \end{align*}$$
$$\begin{align*}\sum_{v_2(n) = j} \frac{r(n,\psi)}{\tau(n^{\flat})} z^{\Omega(n)} e^{-n/N} \ll N(\log N)^{-100}. \end{align*}$$
By Fourier inversion,
 $$\begin{align*}\sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi)}{\tau(n^{\flat})} = \frac{1}{2\pi} \int_{0}^{2\pi} e^{-ik\theta} d\theta \sum_{v_2(n) = j} \frac{r(n,\psi)}{\tau(n^{\flat})} e^{i\theta \Omega(n)} e^{-n/N} \ll N(\log N)^{-100}, \end{align*}$$
$$\begin{align*}\sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi)}{\tau(n^{\flat})} = \frac{1}{2\pi} \int_{0}^{2\pi} e^{-ik\theta} d\theta \sum_{v_2(n) = j} \frac{r(n,\psi)}{\tau(n^{\flat})} e^{i\theta \Omega(n)} e^{-n/N} \ll N(\log N)^{-100}, \end{align*}$$
and the proof of Lemma 8.2 is complete.
To state the other two lemmas of this section, we first need to isolate the genus characters which play a special role. The genus characters for a quadratic field are the class group characters that take only the real values
![]() $\pm 1$
. We will only need to know what these are in the case d prime, in which case the classification is as follows.
$\pm 1$
. We will only need to know what these are in the case d prime, in which case the classification is as follows.
Proposition 8.3. Let d be an odd prime, and let D be the associated fundamental discriminant as in (3.5). Let
![]() $K = \mathbf {Q}(\sqrt {D})$
.
$K = \mathbf {Q}(\sqrt {D})$
.
-
1. If
 $d \equiv 3 \ (\operatorname {mod}\, 4)$
, so
$d \equiv 3 \ (\operatorname {mod}\, 4)$
, so
 $D = -d$
, then there is only one genus character in
$D = -d$
, then there is only one genus character in
 $\widehat {C}_K$
, namely the principal character
$\widehat {C}_K$
, namely the principal character
 $\psi _0$
. The corresponding class group L-function is the Dedekind zeta-function of K, given by
$\psi _0$
. The corresponding class group L-function is the Dedekind zeta-function of K, given by  $$ \begin{align*}L_K(s,\psi_0) = \zeta_K(s) = \zeta(s) L(s,\chi_{D}). \end{align*} $$
$$ \begin{align*}L_K(s,\psi_0) = \zeta_K(s) = \zeta(s) L(s,\chi_{D}). \end{align*} $$
-
2. If
 $d \equiv 1\ (\operatorname {mod}\, 4)$
, so
$d \equiv 1\ (\operatorname {mod}\, 4)$
, so
 $D = -4d$
, then there are two genus characters in
$D = -4d$
, then there are two genus characters in
 $\widehat {C}_K$
: the principal character
$\widehat {C}_K$
: the principal character
 $\psi _0$
, whose L-function is equal to the Dedekind zeta-function of K as above and a nontrivial genus character
$\psi _0$
, whose L-function is equal to the Dedekind zeta-function of K as above and a nontrivial genus character
 $\psi _1$
. On prime ideals
$\psi _1$
. On prime ideals
 $\mathfrak {p}$
,
$\mathfrak {p}$
,
 $\psi _1$
is given by
$\psi _1$
is given by
 $\psi _1(\mathfrak {p}) = \chi _{-4}(N\mathfrak {p})$
if
$\psi _1(\mathfrak {p}) = \chi _{-4}(N\mathfrak {p})$
if
 $\mathfrak {p}$
lies above an odd prime, and
$\mathfrak {p}$
lies above an odd prime, and
 $\psi (\mathfrak {p}) = \chi _{d}(2)$
if
$\psi (\mathfrak {p}) = \chi _{d}(2)$
if
 $\mathfrak {p}$
is the (unique, ramified) prime ideal above
$\mathfrak {p}$
is the (unique, ramified) prime ideal above
 $2$
. The corresponding L-function is given by
$2$
. The corresponding L-function is given by
 $L_K(s,\psi _1) = L(s,\chi _{-4}) L(s,\chi _{d})$
.
$L_K(s,\psi _1) = L(s,\chi _{-4}) L(s,\chi _{d})$
.
Proof. There is a bijective correspondence between genus characters of imaginary quadratic fields of discriminant D and factorizations
![]() $D = D' \cdot D"$
into fundamental discriminants, with the decomposition
$D = D' \cdot D"$
into fundamental discriminants, with the decomposition
![]() $D = 1 \cdot D$
being allowed, and with decompositions different only in the order of
$D = 1 \cdot D$
being allowed, and with decompositions different only in the order of
![]() $D, D"$
being considered equivalent. See [Reference Zagier19, Chapter 12, Satz 2] for a discussion of this, as well as a discussion of how to compute these factorisations in terms of the factorisation of D into prime discriminants. For us, the factorisations can easily be computed by hand: If
$D, D"$
being considered equivalent. See [Reference Zagier19, Chapter 12, Satz 2] for a discussion of this, as well as a discussion of how to compute these factorisations in terms of the factorisation of D into prime discriminants. For us, the factorisations can easily be computed by hand: If
![]() $d \equiv 3\ (\operatorname {mod}\, 4)$
, then there is only the trivial factorisation, whilst when
$d \equiv 3\ (\operatorname {mod}\, 4)$
, then there is only the trivial factorisation, whilst when
![]() $d \equiv 1\ (\operatorname {mod}\, 4)$
, in which case
$d \equiv 1\ (\operatorname {mod}\, 4)$
, in which case
![]() $D = -4d$
, we additionally have the factorisation in which
$D = -4d$
, we additionally have the factorisation in which
![]() $D' = -4$
and
$D' = -4$
and
![]() $D" = d$
.
$D" = d$
.
In [Reference Zagier19, Chapter 12, Satz 2], one may also find the description of a genus character
![]() $\psi $
corresponding to a given factorisation
$\psi $
corresponding to a given factorisation
![]() $D = D' \cdot D"$
: It is given on prime ideals by
$D = D' \cdot D"$
: It is given on prime ideals by
 $$\begin{align*}\psi(\mathfrak{p}) = \left\{ \begin{array}{ll} \chi_{D'} (N\mathfrak{p}) & (N\mathfrak{p}, D') = 1\\ \chi_{D"}(N\mathfrak{p}) & (N\mathfrak{p}, D") = 1\end{array} \right. \end{align*}$$
$$\begin{align*}\psi(\mathfrak{p}) = \left\{ \begin{array}{ll} \chi_{D'} (N\mathfrak{p}) & (N\mathfrak{p}, D') = 1\\ \chi_{D"}(N\mathfrak{p}) & (N\mathfrak{p}, D") = 1\end{array} \right. \end{align*}$$
(That this is well defined is part of the statement.) We have the Kronecker factorisation of L-functions
Specialising to the specific case
![]() $D' = -4$
,
$D' = -4$
,
![]() $D" = d$
gives the stated result.
$D" = d$
gives the stated result.
Lemma 8.4. Let N be large and k be an integer in the range (5.5). Let j be
![]() $0$
or
$0$
or
![]() $1$
, and let d and
$1$
, and let d and
![]() ${\widetilde d}$
be two distinct elements of
${\widetilde d}$
be two distinct elements of
![]() ${\mathcal D}_j$
with D and
${\mathcal D}_j$
with D and
![]() ${\widetilde D}$
denoting the corresponding fundamental discriminants. Let
${\widetilde D}$
denoting the corresponding fundamental discriminants. Let
![]() $\psi $
and
$\psi $
and
![]() ${\widetilde \psi }$
be characters of the class groups of
${\widetilde \psi }$
be characters of the class groups of
![]() $K =\mathbf {Q}(\sqrt {D})$
and
$K =\mathbf {Q}(\sqrt {D})$
and
![]() ${\widetilde K} = \mathbf {Q}(\sqrt {{\widetilde D}})$
respectively. Then
${\widetilde K} = \mathbf {Q}(\sqrt {{\widetilde D}})$
respectively. Then
 $$\begin{align*}\sum_{n \in {\mathcal A}_j(k) } \frac{r(n,\psi) r(n, {\widetilde \psi})}{\tau(n^{\flat})^2} e^{-n/N } \ll N(\log N)^{-100} \end{align*}$$
$$\begin{align*}\sum_{n \in {\mathcal A}_j(k) } \frac{r(n,\psi) r(n, {\widetilde \psi})}{\tau(n^{\flat})^2} e^{-n/N } \ll N(\log N)^{-100} \end{align*}$$
unless (i)
![]() $\psi $
and
$\psi $
and
![]() ${\widetilde \psi }$
are the principal characters in their respective class groups, or (ii) both
${\widetilde \psi }$
are the principal characters in their respective class groups, or (ii) both
![]() $\psi $
and
$\psi $
and
![]() ${\widetilde \psi }$
are the nonprincipal genus character in their respective class groups (and this possibility occurs only in the case
${\widetilde \psi }$
are the nonprincipal genus character in their respective class groups (and this possibility occurs only in the case
![]() $j=1$
).
$j=1$
).
Proof. Given two characters
![]() $\psi \in {\widehat C}_K$
and
$\psi \in {\widehat C}_K$
and
![]() ${\widetilde \psi } \in {\widehat C}_{\widetilde K}$
, we may find a class group character
${\widetilde \psi } \in {\widehat C}_{\widetilde K}$
, we may find a class group character
![]() $\Psi $
on the biquadratic field
$\Psi $
on the biquadratic field
![]() $L=\mathbf {Q}(\sqrt {D}, \sqrt {{\widetilde D}})$
such that for all unramified primes p
$L=\mathbf {Q}(\sqrt {D}, \sqrt {{\widetilde D}})$
such that for all unramified primes p
 $$\begin{align*}\sum_{\substack{ {\mathfrak P} \subset {\mathcal O}_L \\ N_{L/\mathbf{Q}}(\mathfrak P)=p}} \Psi(\mathfrak P) = \Big( \sum_{\substack{ {\mathfrak p} \subset {\mathcal O}_K \\ N_{K/\mathbf{Q}}(\mathfrak p) = p} }\psi({\mathfrak p}) \Big) \Big( \sum_{\substack{ \widetilde{\mathfrak{p}} \subset {\mathcal O}_{\widetilde K} \\ N_{\widetilde{K}/\mathbf{Q}}(\widetilde{\mathfrak{p}}) = p }} {\widetilde \psi}(\widetilde{ \mathfrak p}) \Big) = r(p, \psi) r(p, \widetilde \psi). \end{align*}$$
$$\begin{align*}\sum_{\substack{ {\mathfrak P} \subset {\mathcal O}_L \\ N_{L/\mathbf{Q}}(\mathfrak P)=p}} \Psi(\mathfrak P) = \Big( \sum_{\substack{ {\mathfrak p} \subset {\mathcal O}_K \\ N_{K/\mathbf{Q}}(\mathfrak p) = p} }\psi({\mathfrak p}) \Big) \Big( \sum_{\substack{ \widetilde{\mathfrak{p}} \subset {\mathcal O}_{\widetilde K} \\ N_{\widetilde{K}/\mathbf{Q}}(\widetilde{\mathfrak{p}}) = p }} {\widetilde \psi}(\widetilde{ \mathfrak p}) \Big) = r(p, \psi) r(p, \widetilde \psi). \end{align*}$$
The character
![]() $\Psi $
is defined by setting
$\Psi $
is defined by setting
where
![]() $N_{L/K}$
denotes the ideal norm from L to K (and similarly for
$N_{L/K}$
denotes the ideal norm from L to K (and similarly for
![]() ${\widetilde K}$
), and by Diao [Reference Diao7, Lemma 6], we may check that
${\widetilde K}$
), and by Diao [Reference Diao7, Lemma 6], we may check that
![]() $\Psi $
is nonprincipal except in the cases (i) and (ii) described in the lemma. (Precisely, Lemma 6 of Diao [Reference Diao7] shows that
$\Psi $
is nonprincipal except in the cases (i) and (ii) described in the lemma. (Precisely, Lemma 6 of Diao [Reference Diao7] shows that
![]() $\Psi $
can be principal only if
$\Psi $
can be principal only if
![]() $\psi $
and
$\psi $
and
![]() ${\widetilde \psi }$
are genus (or real) characters. The last remaining case when one of
${\widetilde \psi }$
are genus (or real) characters. The last remaining case when one of
![]() $\psi $
or
$\psi $
or
![]() ${\widetilde \psi }$
is principal while the other equals a nonprincipal genus character is easily checked directly.) Therefore, we may write for any complex number z with
${\widetilde \psi }$
is principal while the other equals a nonprincipal genus character is easily checked directly.) Therefore, we may write for any complex number z with
![]() $|z|=1$
$|z|=1$
 $$\begin{align*}\sum_{v_2(n) = j} \frac{r(n,\psi) r(n,{\widetilde \psi})}{\tau(n^{\flat})^2} z^{\Omega(n)}n^{-s} = L(s,\Psi)^z {\mathcal G}(s;z,j), \end{align*}$$
$$\begin{align*}\sum_{v_2(n) = j} \frac{r(n,\psi) r(n,{\widetilde \psi})}{\tau(n^{\flat})^2} z^{\Omega(n)}n^{-s} = L(s,\Psi)^z {\mathcal G}(s;z,j), \end{align*}$$
where
![]() ${\mathcal G}(s;z,j)$
is given by a suitable Euler product which converges absolutely in Re
${\mathcal G}(s;z,j)$
is given by a suitable Euler product which converges absolutely in Re
![]() $(s) \geq \frac 34$
and satisfies in that region
$(s) \geq \frac 34$
and satisfies in that region
Since the discriminant of L is
![]() $\ll \Delta ^4$
, using Lemma 8.1 and arguing exactly as in our proof of Lemma 8.2 we establish that
$\ll \Delta ^4$
, using Lemma 8.1 and arguing exactly as in our proof of Lemma 8.2 we establish that
 $$\begin{align*}\sum_{v_2(n) = j} \frac{r(n,\psi) r(n,{\widetilde \psi})}{\tau(n^{\flat})^2} z^{\Omega(n)} e^{-n/N} \ll N(\log N)^{-100}, \end{align*}$$
$$\begin{align*}\sum_{v_2(n) = j} \frac{r(n,\psi) r(n,{\widetilde \psi})}{\tau(n^{\flat})^2} z^{\Omega(n)} e^{-n/N} \ll N(\log N)^{-100}, \end{align*}$$
and then the bound of the lemma follows by an application of Fourier inversion.
Lemma 8.5. Let N be large and k be an integer in the range (5.5). Let j be
![]() $0$
or
$0$
or
![]() $1$
, and let d be an element of
$1$
, and let d be an element of
![]() ${\mathcal D}_j$
with D denoting the corresponding fundamental discriminant. Let
${\mathcal D}_j$
with D denoting the corresponding fundamental discriminant. Let
![]() $\psi $
and
$\psi $
and
![]() ${\widetilde \psi }$
be two characters of the class group of
${\widetilde \psi }$
be two characters of the class group of
![]() $K =\mathbf {Q}(\sqrt {D})$
, and suppose that neither
$K =\mathbf {Q}(\sqrt {D})$
, and suppose that neither
![]() $\psi $
nor
$\psi $
nor
![]() $\overline {\psi }$
is equal to
$\overline {\psi }$
is equal to
![]() ${\widetilde \psi }$
. Then
${\widetilde \psi }$
. Then
 $$ \begin{align*}\sum_{n \in {\mathcal A}_j(k) } \frac{r(n,\psi) r(n, {\widetilde \psi})}{\tau(n^{\flat})^2} e^{-n/N } \ll N(\log N)^{-100}. \end{align*} $$
$$ \begin{align*}\sum_{n \in {\mathcal A}_j(k) } \frac{r(n,\psi) r(n, {\widetilde \psi})}{\tau(n^{\flat})^2} e^{-n/N } \ll N(\log N)^{-100}. \end{align*} $$
Proof. For an unramified prime p, we have
To see this, note that if p is inert, then
![]() $r(p,\psi )=r(p,\widetilde {\psi })=r(p,\psi \widetilde \psi )=r(p,\overline {\psi } \widetilde \psi )=0$
, while if p splits as
$r(p,\psi )=r(p,\widetilde {\psi })=r(p,\psi \widetilde \psi )=r(p,\overline {\psi } \widetilde \psi )=0$
, while if p splits as
![]() ${\mathfrak p}\overline {\mathfrak p}$
, then
${\mathfrak p}\overline {\mathfrak p}$
, then
![]() $r(p,\psi )=\psi (\mathfrak {p}) + \overline {\psi }(\mathfrak {p})$
(and similarly for the other quantities) so that the stated relation follows with a little algebra. It follows that for any complex number z with
$r(p,\psi )=\psi (\mathfrak {p}) + \overline {\psi }(\mathfrak {p})$
(and similarly for the other quantities) so that the stated relation follows with a little algebra. It follows that for any complex number z with
![]() $|z|=1$
we may write
$|z|=1$
we may write
 $$\begin{align*}\sum_{v_2(n) = j} \frac{r(n,\psi) r(n,{\widetilde \psi})}{\tau(n^{\flat})^2} z^{\Omega(n)} n^{-s} = L(s,\psi {\widetilde \psi})^z L(s, \overline{\psi} \widetilde{\psi})^z {\mathcal G}(s;z,j), \end{align*}$$
$$\begin{align*}\sum_{v_2(n) = j} \frac{r(n,\psi) r(n,{\widetilde \psi})}{\tau(n^{\flat})^2} z^{\Omega(n)} n^{-s} = L(s,\psi {\widetilde \psi})^z L(s, \overline{\psi} \widetilde{\psi})^z {\mathcal G}(s;z,j), \end{align*}$$
where
![]() ${\mathcal G}(s;z,j)$
is given by a suitable Euler product which converges absolutely in Re
${\mathcal G}(s;z,j)$
is given by a suitable Euler product which converges absolutely in Re
![]() $(s) \geq \frac 34$
and satisfies in that region
$(s) \geq \frac 34$
and satisfies in that region
By hypothesis, both
![]() $\psi \widetilde {\psi }$
and
$\psi \widetilde {\psi }$
and
![]() $\overline {\psi } \widetilde {\psi }$
are nonprincipal characters of the class group of K, and therefore arguing exactly as in Lemma 8.2 and Lemma 8.4, we obtain the lemma.
$\overline {\psi } \widetilde {\psi }$
are nonprincipal characters of the class group of K, and therefore arguing exactly as in Lemma 8.2 and Lemma 8.4, we obtain the lemma.
9 Proof of Proposition 5.2
In this section, we prove Proposition 5.2. Using (3.4), we may write
 $$\begin{align*}\sum_{n \in {\mathcal A}_j(k)} \frac{R_D(n)}{\tau(n^{\flat})} e^{-n/N} = \frac{1}{h_K} \sum_{\psi \in {\widehat C}_K} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi)}{\tau(n^{\flat})} e^{-n/N}. \end{align*}$$
$$\begin{align*}\sum_{n \in {\mathcal A}_j(k)} \frac{R_D(n)}{\tau(n^{\flat})} e^{-n/N} = \frac{1}{h_K} \sum_{\psi \in {\widehat C}_K} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi)}{\tau(n^{\flat})} e^{-n/N}. \end{align*}$$
By Lemma 8.2, the contribution of the nonprincipal characters is
![]() $\ll N(\log N)^{-100}$
. Thus,
$\ll N(\log N)^{-100}$
. Thus,
 $$ \begin{align} \sum_{n \in {\mathcal A}_j(k)} \frac{R_D(n)}{\tau(n^{\flat})} e^{-n/N} = \frac{1}{h_K} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi_0)}{\tau(n^{\flat})} e^{-n/N} + O\big( N(\log N)^{-100}\big), \end{align} $$
$$ \begin{align} \sum_{n \in {\mathcal A}_j(k)} \frac{R_D(n)}{\tau(n^{\flat})} e^{-n/N} = \frac{1}{h_K} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi_0)}{\tau(n^{\flat})} e^{-n/N} + O\big( N(\log N)^{-100}\big), \end{align} $$
where
![]() $\psi _0$
is the trivial character.
$\psi _0$
is the trivial character.
To understand the main term on the right-hand side of (9.1), we will again follow Selberg [Reference Selberg16] and introduce for any
![]() $z \in \mathbf {C}$
with
$z \in \mathbf {C}$
with
![]() $|z| = 1$
the Dirichlet series
$|z| = 1$
the Dirichlet series
 $$ \begin{align} \mathcal{F}(s; z, j) := \sum_{v_2(n) = j } \frac{r(n,\psi_0)}{\tau(n^{\flat}) } z^{\Omega(n)} n^{-s}, \end{align} $$
$$ \begin{align} \mathcal{F}(s; z, j) := \sum_{v_2(n) = j } \frac{r(n,\psi_0)}{\tau(n^{\flat}) } z^{\Omega(n)} n^{-s}, \end{align} $$
which to begin with converges absolutely for
![]() $\sigma =\text {Re}(s)>1$
and defines a holomorphic function there. As in Selberg’s work, we will find that
$\sigma =\text {Re}(s)>1$
and defines a holomorphic function there. As in Selberg’s work, we will find that
![]() $\mathcal {F}$
can be understood in terms of the complex powers of
$\mathcal {F}$
can be understood in terms of the complex powers of
![]() $\zeta $
and L-functions, thereby obtaining an analytic continuation of
$\zeta $
and L-functions, thereby obtaining an analytic continuation of
![]() ${\mathcal F}$
to a wider region. The sum in (9.1) can be expressed in terms of a contour integral involving
${\mathcal F}$
to a wider region. The sum in (9.1) can be expressed in terms of a contour integral involving
![]() ${\mathcal F}(s)$
, which can then be evaluated using the analytic continuation of
${\mathcal F}(s)$
, which can then be evaluated using the analytic continuation of
![]() ${\mathcal F}$
and an argument involving a Hankel contour. Since we need to keep track of the uniformity in d, we give a self-contained account in Appendix A.
${\mathcal F}$
and an argument involving a Hankel contour. Since we need to keep track of the uniformity in d, we give a self-contained account in Appendix A.
Let us turn to the details. We obtain an analytic continuation of
![]() ${\mathcal F}$
to a wider region by writing
${\mathcal F}$
to a wider region by writing
Note that
![]() $\zeta (s) L(s,\chi _D)$
is the Dedekind zeta-function of the quadratic field
$\zeta (s) L(s,\chi _D)$
is the Dedekind zeta-function of the quadratic field
![]() $\mathbf {Q}(\sqrt {D})$
, and by
$\mathbf {Q}(\sqrt {D})$
, and by
![]() $(\zeta (s) L(s,\chi _D))^z$
, we mean
$(\zeta (s) L(s,\chi _D))^z$
, we mean
![]() $\exp (z\log (\zeta (s) L(s,\chi _D))$
, where the logarithm is initially defined in
$\exp (z\log (\zeta (s) L(s,\chi _D))$
, where the logarithm is initially defined in
![]() $\sigma>1$
by an absolutely convergent Dirichlet series as in (8.2). Thus, (9.3) should be thought of as the definition of the function
$\sigma>1$
by an absolutely convergent Dirichlet series as in (8.2). Thus, (9.3) should be thought of as the definition of the function
![]() ${\mathcal G}(s;z,j)$
, which is holomorphic in the half-plane
${\mathcal G}(s;z,j)$
, which is holomorphic in the half-plane
![]() $\sigma>1$
. We shall shortly see that
$\sigma>1$
. We shall shortly see that
![]() ${\mathcal G}(s;z,j)$
is analytic in
${\mathcal G}(s;z,j)$
is analytic in
![]() $\sigma> \frac 12$
with suitable bounds in that region. By part (2) of Lemma 8.1, we may obtain an analytic continuation of
$\sigma> \frac 12$
with suitable bounds in that region. By part (2) of Lemma 8.1, we may obtain an analytic continuation of
![]() $\log ((s-1)\zeta (s) L(s,\chi _D))$
to the region
$\log ((s-1)\zeta (s) L(s,\chi _D))$
to the region
![]() ${\mathcal R}_0$
with corresponding bounds in the region
${\mathcal R}_0$
with corresponding bounds in the region
![]() ${\mathcal R}$
. In this way, we obtain a continuation of
${\mathcal R}$
. In this way, we obtain a continuation of
![]() ${\mathcal F}(s;z,j)$
(essentially) to the region
${\mathcal F}(s;z,j)$
(essentially) to the region
![]() ${\mathcal R}$
, except that we must omit the real line segment to the left of
${\mathcal R}$
, except that we must omit the real line segment to the left of
![]() $s=1$
owing to the logarithmic singularity at
$s=1$
owing to the logarithmic singularity at
![]() $s=1$
.
$s=1$
.
From the multiplicative nature of the definition of
![]() $\mathcal {F}(s;z,j)$
, in the region
$\mathcal {F}(s;z,j)$
, in the region
![]() $\sigma>1$
we see that
$\sigma>1$
we see that
![]() ${\mathcal G}(s;z,j)$
is given by an Euler product
${\mathcal G}(s;z,j)$
is given by an Euler product
![]() $\prod _{p} {\mathcal G}(s;z,j)$
. We now describe these Euler factors. If
$\prod _{p} {\mathcal G}(s;z,j)$
. We now describe these Euler factors. If
![]() $p>W$
, we have
$p>W$
, we have
 $$ \begin{align} {\mathcal G}_p(s;z,j) = \left(\sum_{\ell =0}^{\infty} r(p^{\ell}, \psi_0) z^{\ell} p^{-\ell s} \right) \big(1- p^{-s}\big)^z \big( 1- \chi_D(p)p^{-s} \big)^z, \end{align} $$
$$ \begin{align} {\mathcal G}_p(s;z,j) = \left(\sum_{\ell =0}^{\infty} r(p^{\ell}, \psi_0) z^{\ell} p^{-\ell s} \right) \big(1- p^{-s}\big)^z \big( 1- \chi_D(p)p^{-s} \big)^z, \end{align} $$
and since
![]() $r(p,\psi _0) = 1+ \chi _D(p)$
and
$r(p,\psi _0) = 1+ \chi _D(p)$
and
![]() $0\leq r(p^\ell ,\psi _0)\leq (\ell +1)$
it follows that
$0\leq r(p^\ell ,\psi _0)\leq (\ell +1)$
it follows that
 $$ \begin{align} \nonumber {\mathcal G}_p(s;z,j) &= \big( 1 + (1+\chi_D(p)) z p^{-s} + O(p^{-2\sigma})\big) \big( 1 - (1+\chi_D(p)) z p^{-s} + O(p^{-2\sigma})\big) \\ & = 1 + O(p^{-2\sigma}). \end{align} $$
$$ \begin{align} \nonumber {\mathcal G}_p(s;z,j) &= \big( 1 + (1+\chi_D(p)) z p^{-s} + O(p^{-2\sigma})\big) \big( 1 - (1+\chi_D(p)) z p^{-s} + O(p^{-2\sigma})\big) \\ & = 1 + O(p^{-2\sigma}). \end{align} $$
For
![]() $3\leq p\leq W$
, from our choice (5.2), (5.3) of d, we have
$3\leq p\leq W$
, from our choice (5.2), (5.3) of d, we have
![]() $\chi _D(p)=1$
so that
$\chi _D(p)=1$
so that
![]() $r(p^{\ell },\psi _0) = (1 \ast \chi _D)(p^{\ell }) = \ell +1$
. Thus,
$r(p^{\ell },\psi _0) = (1 \ast \chi _D)(p^{\ell }) = \ell +1$
. Thus,
 $$ \begin{align} {\mathcal G}_p(s;z,j) = \Big(\sum_{\ell =0}^{\infty} \frac{r(p^{\ell}, \psi_0)}{\ell+1} z^{\ell} p^{-\ell s} \Big) \big(1- p^{-s}\big)^z \big( 1- p^{-s} \big)^z = \big( 1- z p^{-s} \big)^{-1} \big( 1-p^{-s}\big)^{2z}. \end{align} $$
$$ \begin{align} {\mathcal G}_p(s;z,j) = \Big(\sum_{\ell =0}^{\infty} \frac{r(p^{\ell}, \psi_0)}{\ell+1} z^{\ell} p^{-\ell s} \Big) \big(1- p^{-s}\big)^z \big( 1- p^{-s} \big)^z = \big( 1- z p^{-s} \big)^{-1} \big( 1-p^{-s}\big)^{2z}. \end{align} $$
As we have just seen, for the primes
![]() $p\geq 3$
there is no dependence on j. By contrast, for
$p\geq 3$
there is no dependence on j. By contrast, for
![]() $p=2$
the behaviour is different in the two cases
$p=2$
the behaviour is different in the two cases
![]() $j=0$
(where
$j=0$
(where
![]() $\chi _D(2)=1$
) and
$\chi _D(2)=1$
) and
![]() $j=1$
(where
$j=1$
(where
![]() $\chi _D(2)=0$
). Here, we find
$\chi _D(2)=0$
). Here, we find
 $$ \begin{align} {\mathcal G}_2(s;z,j) = \begin{cases} (1-2^{-s})^{2z} &\text{ if } j=0\\ z2^{-s-1} (1-2^{-s})^z &\text{ if } j=1. \end{cases} \end{align} $$
$$ \begin{align} {\mathcal G}_2(s;z,j) = \begin{cases} (1-2^{-s})^{2z} &\text{ if } j=0\\ z2^{-s-1} (1-2^{-s})^z &\text{ if } j=1. \end{cases} \end{align} $$
From (9.6) and (9.7). note that for all
![]() $p\leq W$
(and uniformly for
$p\leq W$
(and uniformly for
![]() $|z| = 1$
)
$|z| = 1$
)
From (9.5) and (9.8), we see that the Euler product
![]() $\prod _{p} {\mathcal G}_p(s;z,j)$
, which was known initially to converge absolutely in
$\prod _{p} {\mathcal G}_p(s;z,j)$
, which was known initially to converge absolutely in
![]() ${\operatorname {Re}} s =\sigma>1$
, in fact converges absolutely for
${\operatorname {Re}} s =\sigma>1$
, in fact converges absolutely for
![]() $\sigma>\frac 12$
. Moreover, for
$\sigma>\frac 12$
. Moreover, for
![]() $\sigma \geq \frac 34$
we deduce that
$\sigma \geq \frac 34$
we deduce that
 $$ \begin{align} |{\mathcal G}(s;z,j)| \ll \exp\Big( \sum_{p\leq W} O(p^{-3/4}) \Big) \ll \exp(W^{1/4}). \end{align} $$
$$ \begin{align} |{\mathcal G}(s;z,j)| \ll \exp\Big( \sum_{p\leq W} O(p^{-3/4}) \Big) \ll \exp(W^{1/4}). \end{align} $$
Now, we apply Selberg’s method as explained in Appendix A. Specifically, by (A.7) and (A.8), we obtain
 $$ \begin{align} \sum_{ v_2(n) = j} \frac{r(n, \psi_0)}{\tau(n^{\flat})} z^{\Omega(n)} e^{-n/N} = {N} \frac{(\log N)^{z-1}}{\Gamma(z)} L(1,\chi_{D})^z {\mathcal G}(1;z,j) + O_{\varepsilon}\Big( N (\log N)^{{\operatorname{Re}} z -\frac 32 + \varepsilon}\Big). \end{align} $$
$$ \begin{align} \sum_{ v_2(n) = j} \frac{r(n, \psi_0)}{\tau(n^{\flat})} z^{\Omega(n)} e^{-n/N} = {N} \frac{(\log N)^{z-1}}{\Gamma(z)} L(1,\chi_{D})^z {\mathcal G}(1;z,j) + O_{\varepsilon}\Big( N (\log N)^{{\operatorname{Re}} z -\frac 32 + \varepsilon}\Big). \end{align} $$
Applying the above with
![]() $z= e^{i\theta }$
for
$z= e^{i\theta }$
for
![]() $-\pi \leq \theta \leq \pi $
and applying orthogonality (Fourier inversion), we deduce that
$-\pi \leq \theta \leq \pi $
and applying orthogonality (Fourier inversion), we deduce that
 $$ \begin{align} \nonumber \sum_{\substack{n \in {\mathcal A}_j(k)}} &\frac{r(n,\psi_0)}{\tau(n^{\flat})} e^{-n/N} = \frac{1}{2\pi} \int_{-\pi}^{\pi} \sum_{v_2(n) = j} \frac{r(n, \psi_0)}{\tau(n^{\flat})} e^{i\theta \Omega(n)} e^{-n/N} e^{-ik\theta} d\theta \nonumber \\ &= \frac{N}{\log N} \frac{1}{2\pi} \int_{-\pi}^{\pi} (L(1,\chi_{D}) \log N)^{e^{i \theta}} \frac{{\mathcal G}(1;e^{i\theta},j)}{\Gamma(e^{i\theta})} e^{-ik\theta} d\theta +O_{\varepsilon}\big( N (\log N)^{\varepsilon - 1/2} \big). \end{align} $$
$$ \begin{align} \nonumber \sum_{\substack{n \in {\mathcal A}_j(k)}} &\frac{r(n,\psi_0)}{\tau(n^{\flat})} e^{-n/N} = \frac{1}{2\pi} \int_{-\pi}^{\pi} \sum_{v_2(n) = j} \frac{r(n, \psi_0)}{\tau(n^{\flat})} e^{i\theta \Omega(n)} e^{-n/N} e^{-ik\theta} d\theta \nonumber \\ &= \frac{N}{\log N} \frac{1}{2\pi} \int_{-\pi}^{\pi} (L(1,\chi_{D}) \log N)^{e^{i \theta}} \frac{{\mathcal G}(1;e^{i\theta},j)}{\Gamma(e^{i\theta})} e^{-ik\theta} d\theta +O_{\varepsilon}\big( N (\log N)^{\varepsilon - 1/2} \big). \end{align} $$
We now simplify the main term appearing in (9.11). Since
![]() $1/\Gamma (z)$
is entire, uniformly for
$1/\Gamma (z)$
is entire, uniformly for
![]() $\theta \in [-\pi ,\pi ]$
we have
$\theta \in [-\pi ,\pi ]$
we have
Now, from its definition in (9.4) we may see that for
![]() $p>W$
$p>W$
 $$ \begin{align*} \frac{d}{d\phi} & \log {\mathcal G}_p(1;e^{i\phi}, j) = i \frac{\sum_{\ell=1}^{\infty} \ell r(p^\ell, \psi_0)e^{i\ell \phi} p^{-\ell}}{\sum_{\ell =0}^{\infty} r(p^\ell, \psi_0) e^{i\ell \phi}p^{-\ell}} +i e^{i\phi} \log \big( (1 - p^{-1}) (1 - \chi_D(p) p^{-1}) \big) \\ & = i \frac{e^{i\phi} r(p,\psi_0)/p + O(1/p^2)}{1+O(1/p)} - ie^{i\phi}\big( (1+\chi_D(p)) p^{-1} +O(p^{-2}) \big) = O(p^{-2}). \end{align*} $$
$$ \begin{align*} \frac{d}{d\phi} & \log {\mathcal G}_p(1;e^{i\phi}, j) = i \frac{\sum_{\ell=1}^{\infty} \ell r(p^\ell, \psi_0)e^{i\ell \phi} p^{-\ell}}{\sum_{\ell =0}^{\infty} r(p^\ell, \psi_0) e^{i\ell \phi}p^{-\ell}} +i e^{i\phi} \log \big( (1 - p^{-1}) (1 - \chi_D(p) p^{-1}) \big) \\ & = i \frac{e^{i\phi} r(p,\psi_0)/p + O(1/p^2)}{1+O(1/p)} - ie^{i\phi}\big( (1+\chi_D(p)) p^{-1} +O(p^{-2}) \big) = O(p^{-2}). \end{align*} $$
Integrating this over
![]() $\phi $
from
$\phi $
from
![]() $0$
to
$0$
to
![]() $\theta $
we obtain that, for
$\theta $
we obtain that, for
![]() $\theta \in [-\pi , \pi ]$
,
$\theta \in [-\pi , \pi ]$
,
 $$ \begin{align} \frac{{\mathcal G}_p(1;e^{i\theta},j)}{{\mathcal G}_p(1;1,j)} = \exp\big( O (|\theta| p^{-2}) \big) = 1 + O\big( |\theta| p^{-2} \big). \end{align} $$
$$ \begin{align} \frac{{\mathcal G}_p(1;e^{i\theta},j)}{{\mathcal G}_p(1;1,j)} = \exp\big( O (|\theta| p^{-2}) \big) = 1 + O\big( |\theta| p^{-2} \big). \end{align} $$
Similarly, from (9.6) and (9.7) it follows that for all
![]() $p\leq W$
$p\leq W$
 $$ \begin{align} \frac{{\mathcal G}_p(1;e^{i\theta},j)}{{\mathcal G}_p(1;1,j)} = 1 + O \big( |\theta| p^{-1} \big). \end{align} $$
$$ \begin{align} \frac{{\mathcal G}_p(1;e^{i\theta},j)}{{\mathcal G}_p(1;1,j)} = 1 + O \big( |\theta| p^{-1} \big). \end{align} $$
Multiplying the relations in (9.13) and (9.14) over all primes, we conclude that
 $$ \begin{align} \frac{{\mathcal G}(1;e^{i\theta},j)}{{\mathcal G}(1;1,j)} = \exp\Big( O\Big( |\theta| \big( \sum_{p\leq W} p^{-1} + \sum_{p> W} p^{-2} \big) \Big) \Big) = 1+ O(|\theta| (\log W)^C), \end{align} $$
$$ \begin{align} \frac{{\mathcal G}(1;e^{i\theta},j)}{{\mathcal G}(1;1,j)} = \exp\Big( O\Big( |\theta| \big( \sum_{p\leq W} p^{-1} + \sum_{p> W} p^{-2} \big) \Big) \Big) = 1+ O(|\theta| (\log W)^C), \end{align} $$
for some constant C (consider the cases
![]() $|\theta | \leq (\log \log W)^{-1}$
and
$|\theta | \leq (\log \log W)^{-1}$
and
![]() $|\theta |> (\log \log W)^{-1}$
separately).
$|\theta |> (\log \log W)^{-1}$
separately).
For later use, let us record the value of
![]() ${\mathcal G}(1;1,j)$
. For any prime
${\mathcal G}(1;1,j)$
. For any prime
![]() $p>W$
one may see using (9.4) and the identity
$p>W$
one may see using (9.4) and the identity
![]() $\sum _{\ell = 0}^{\infty }\sum _{j = 0}^{\ell } x^j y^{\ell } = (1 - xy)^{-1}(1 - y)^{-1}$
with
$\sum _{\ell = 0}^{\infty }\sum _{j = 0}^{\ell } x^j y^{\ell } = (1 - xy)^{-1}(1 - y)^{-1}$
with
![]() $x = \chi _D(p)$
and
$x = \chi _D(p)$
and
![]() $y = p^{-s}$
that
$y = p^{-s}$
that
![]() ${\mathcal G}_p(s;1,j) =1$
, while for
${\mathcal G}_p(s;1,j) =1$
, while for
![]() $3\leq p \leq W$
it follows from (9.6) that
$3\leq p \leq W$
it follows from (9.6) that
![]() ${\mathcal G}_p(s;1,j) = 1-1/p^{s}$
, and lastly from (9.7) we see that
${\mathcal G}_p(s;1,j) = 1-1/p^{s}$
, and lastly from (9.7) we see that
![]() ${\mathcal G}_2(1;1,j) = 2^{-j-1}(1-2^{-1})$
. Combining these observations, it follows that
${\mathcal G}_2(1;1,j) = 2^{-j-1}(1-2^{-1})$
. Combining these observations, it follows that
Using (9.12), (9.15) and (9.16) we obtain
 $$ \begin{align} \frac{1}{2\pi} \int_{-\pi}^{\pi} (L(1,\chi_{D}) \log N)^{e^{i\theta} }& \frac{{\mathcal G}(1;e^{i\theta},j)}{\Gamma(e^{i\theta})} e^{-ik\theta} d\theta = 2^{-j-1} \gamma_W \frac{(\log (L(1,\chi_{D} )\log N))^{k}}{k!} \nonumber \\ &+O\Big((\log W)^C \int_{-\pi}^{\pi} (L(1,\chi_D)\log N)^{\cos \theta} |\theta| d\theta \Big), \end{align} $$
$$ \begin{align} \frac{1}{2\pi} \int_{-\pi}^{\pi} (L(1,\chi_{D}) \log N)^{e^{i\theta} }& \frac{{\mathcal G}(1;e^{i\theta},j)}{\Gamma(e^{i\theta})} e^{-ik\theta} d\theta = 2^{-j-1} \gamma_W \frac{(\log (L(1,\chi_{D} )\log N))^{k}}{k!} \nonumber \\ &+O\Big((\log W)^C \int_{-\pi}^{\pi} (L(1,\chi_D)\log N)^{\cos \theta} |\theta| d\theta \Big), \end{align} $$
where the main term arises upon noting that, for
![]() $X> 0$
,
$X> 0$
,
 $$\begin{align*}\frac{1}{2\pi} \int_{-\pi}^{\pi} X^{e^{i\theta}} e^{-ik\theta} d\theta =\frac{1}{2\pi} \int_{-\pi}^{\pi} \sum_{\ell=0}^{\infty} \frac{(\log X)^{\ell}}{\ell!} e^{i\ell \theta} e^{-ik\theta} d\theta = \frac{(\log X)^{k}}{k!}. \end{align*}$$
$$\begin{align*}\frac{1}{2\pi} \int_{-\pi}^{\pi} X^{e^{i\theta}} e^{-ik\theta} d\theta =\frac{1}{2\pi} \int_{-\pi}^{\pi} \sum_{\ell=0}^{\infty} \frac{(\log X)^{\ell}}{\ell!} e^{i\ell \theta} e^{-ik\theta} d\theta = \frac{(\log X)^{k}}{k!}. \end{align*}$$
Note that
![]() $\cos \theta \leq 1- \theta ^2/8$
for all
$\cos \theta \leq 1- \theta ^2/8$
for all
![]() $|\theta |\leq \pi $
, and that (by the class number formula (9.22))
$|\theta |\leq \pi $
, and that (by the class number formula (9.22))
![]() $L(1,\chi _D) \geq |D|^{-1/2} \geq (\log N)^{-1/2}$
so that
$L(1,\chi _D) \geq |D|^{-1/2} \geq (\log N)^{-1/2}$
so that
![]() $L(1,\chi _D) \log N \geq (\log N)^{1/2}$
. Therefore, (recalling that
$L(1,\chi _D) \log N \geq (\log N)^{1/2}$
. Therefore, (recalling that
![]() $k_0 = \log \log N$
and that
$k_0 = \log \log N$
and that
![]() $W = \log \log \log N$
)
$W = \log \log \log N$
)
 $$\begin{align*}\int_{-\pi}^{\pi} (L(1,\chi_D)\log N)^{\cos \theta} |\theta| d\theta &\leq (L(1,\chi_D) \log N) \int_{-\pi}^{\pi} (\log N)^{-\theta^2/16} |\theta| d\theta \\ &\ll k_0^{-1} L(1,\chi_D) \log N \end{align*}$$
$$\begin{align*}\int_{-\pi}^{\pi} (L(1,\chi_D)\log N)^{\cos \theta} |\theta| d\theta &\leq (L(1,\chi_D) \log N) \int_{-\pi}^{\pi} (\log N)^{-\theta^2/16} |\theta| d\theta \\ &\ll k_0^{-1} L(1,\chi_D) \log N \end{align*}$$
so that the remainder term in (9.17) is seen to be
Using (9.17) and (9.18) in (9.11), we conclude that
 $$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} \frac{r(n,\psi_0)}{\tau(n^{\flat})} e^{-n/N} = \frac{N}{\log N} \frac{\gamma_W}{2^{j+1}} \frac{(\log (L(1,\chi_D)\log N))^k}{k!} + O\big( Nk_0^{\varepsilon - 1} L(1,\chi_D) \big), \end{align} $$
$$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} \frac{r(n,\psi_0)}{\tau(n^{\flat})} e^{-n/N} = \frac{N}{\log N} \frac{\gamma_W}{2^{j+1}} \frac{(\log (L(1,\chi_D)\log N))^k}{k!} + O\big( Nk_0^{\varepsilon - 1} L(1,\chi_D) \big), \end{align} $$
where we absorbed the error term
![]() $O_{\varepsilon }(N(\log N)^{\varepsilon - 1/2})$
in (9.11) into the error term above using
$O_{\varepsilon }(N(\log N)^{\varepsilon - 1/2})$
in (9.11) into the error term above using
![]() $L(1,\chi _D) \gg _{\varepsilon } |D|^{-\varepsilon } \gg (\log N)^{-\varepsilon }$
.
$L(1,\chi _D) \gg _{\varepsilon } |D|^{-\varepsilon } \gg (\log N)^{-\varepsilon }$
.
We now claim that for k in the range (5.5) and all x with
![]() $(\log N)^{-1/2} \leq x \leq k_0^4$
we have
$(\log N)^{-1/2} \leq x \leq k_0^4$
we have
 $$ \begin{align} \left( \frac{\log (x \log N)}{k_0} \right)^{k} = \left(1 + \frac{\log x}{k_0}\right)^k = x \big( 1+ O_{\varepsilon}(k_0^{\varepsilon - 1/3})\big) + O(k_0^{-3}). \end{align} $$
$$ \begin{align} \left( \frac{\log (x \log N)}{k_0} \right)^{k} = \left(1 + \frac{\log x}{k_0}\right)^k = x \big( 1+ O_{\varepsilon}(k_0^{\varepsilon - 1/3})\big) + O(k_0^{-3}). \end{align} $$
To verify the claim, consider the following two cases: (i) when
![]() $k_0^{-4} \leq x \leq k_0^4$
, and (ii) when
$k_0^{-4} \leq x \leq k_0^4$
, and (ii) when
![]() $(\log N)^{-1/2} \leq x \leq k_0^{-4}$
. In case (i) note that
$(\log N)^{-1/2} \leq x \leq k_0^{-4}$
. In case (i) note that
![]() $|\log x| = O(\log k_0)$
, and so the left-hand side of (9.20) is
$|\log x| = O(\log k_0)$
, and so the left-hand side of (9.20) is
so that the claim follows here. In case (ii), note that since
![]() $k\geq 3k_0/4$
and we have
$k\geq 3k_0/4$
and we have
so (9.20) holds in this case also.
Applying (9.20) with
![]() $x=L(1,\chi _D)$
(which satisfies
$x=L(1,\chi _D)$
(which satisfies
![]() $(\log N)^{-1/2} \leq L(1,\chi _D) \ll \log \log N$
), we see that
$(\log N)^{-1/2} \leq L(1,\chi _D) \ll \log \log N$
), we see that
 $$ \begin{align*} \frac{(\log (L(1,\chi_D)\log N))^k}{k!} &= \frac{k_0^k}{k!} \Big( L(1, \chi_D) + O_{\varepsilon}\big( k_0^{\varepsilon - 1/3} L(1,\chi_D) +k_0^{-3} \big)\Big) \\ &= \frac{k_0^k}{k!} L(1,\chi_D) + O_{\varepsilon}\big( k_0^{\varepsilon - 5/6} L(1,\chi_D)\log N +k_0^{-3} \log N \big), \end{align*} $$
$$ \begin{align*} \frac{(\log (L(1,\chi_D)\log N))^k}{k!} &= \frac{k_0^k}{k!} \Big( L(1, \chi_D) + O_{\varepsilon}\big( k_0^{\varepsilon - 1/3} L(1,\chi_D) +k_0^{-3} \big)\Big) \\ &= \frac{k_0^k}{k!} L(1,\chi_D) + O_{\varepsilon}\big( k_0^{\varepsilon - 5/6} L(1,\chi_D)\log N +k_0^{-3} \log N \big), \end{align*} $$
where the last estimate follows using the bound
![]() $k_0^k/k! \ll k_0^{-1/2} \log N$
, which is a consequence of Stirling’s formula. Using this in (9.19), we conclude that
$k_0^k/k! \ll k_0^{-1/2} \log N$
, which is a consequence of Stirling’s formula. Using this in (9.19), we conclude that
 $$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} \frac{r(n,\psi_0)}{\tau(n^{\flat})} e^{-n/N} = \frac{N}{\log N} \frac{\gamma_W}{2^{j+1}} L(1,\chi_D)\frac{k_0^k}{k!} + O_{\varepsilon}\big( k_0^{\varepsilon - 5/6} NL(1,\chi_D) + k_0^{-3} \log N\big). \end{align} $$
$$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} \frac{r(n,\psi_0)}{\tau(n^{\flat})} e^{-n/N} = \frac{N}{\log N} \frac{\gamma_W}{2^{j+1}} L(1,\chi_D)\frac{k_0^k}{k!} + O_{\varepsilon}\big( k_0^{\varepsilon - 5/6} NL(1,\chi_D) + k_0^{-3} \log N\big). \end{align} $$
Using (9.21) in (9.1) and invoking the class number formula
we obtain (note also that
![]() $\gamma _W \gg (\log W)^{-1} \gg _{\varepsilon } k_0^{-\varepsilon }$
)
$\gamma _W \gg (\log W)^{-1} \gg _{\varepsilon } k_0^{-\varepsilon }$
)
 $$\begin{align*}\frac{|D|^{1/2}}{\pi \gamma_W} \sum_{n\in {\mathcal A}_j(k)} \frac{R_D(n)}{\tau(n^{\flat})} e^{-n/N} = \frac{1}{2^{j+1}} \frac{N}{\log N} \frac{k_0^k}{k!} + O_{\varepsilon}\big( Nk_0^{\varepsilon - 5/6} + N L(1,\chi_D)^{-1} k_0^{-2}\big). \end{align*}$$
$$\begin{align*}\frac{|D|^{1/2}}{\pi \gamma_W} \sum_{n\in {\mathcal A}_j(k)} \frac{R_D(n)}{\tau(n^{\flat})} e^{-n/N} = \frac{1}{2^{j+1}} \frac{N}{\log N} \frac{k_0^k}{k!} + O_{\varepsilon}\big( Nk_0^{\varepsilon - 5/6} + N L(1,\chi_D)^{-1} k_0^{-2}\big). \end{align*}$$
10 Proof of Proposition 5.3
We turn now to the proof of Proposition 5.3. We first dispense with the case when
![]() $d\not \equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
which, recalling the definitions (5.2) and (5.3), can only happen in the case
$d\not \equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
which, recalling the definitions (5.2) and (5.3), can only happen in the case
![]() $j = 1$
. Note that if
$j = 1$
. Note that if
![]() $d \equiv 1 \ (\operatorname {mod}\, 8)$
, then the integers n with
$d \equiv 1 \ (\operatorname {mod}\, 8)$
, then the integers n with
![]() $n \equiv 2 \ (\operatorname {mod}\, 4)$
that are represented by
$n \equiv 2 \ (\operatorname {mod}\, 4)$
that are represented by
![]() $x^2+dy^2$
satisfy
$x^2+dy^2$
satisfy
![]() $n\equiv 2 \ (\operatorname {mod}\, 8)$
, while if
$n\equiv 2 \ (\operatorname {mod}\, 8)$
, while if
![]() $d\equiv 5 \ (\operatorname {mod}\, 8)$
, then such integers n must be
$d\equiv 5 \ (\operatorname {mod}\, 8)$
, then such integers n must be
![]() $\equiv 6 \ (\operatorname {mod}\, 8)$
. Thus, if
$\equiv 6 \ (\operatorname {mod}\, 8)$
. Thus, if
![]() $d \not \equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
and if
$d \not \equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
and if
![]() $n \in \mathcal {A}_1(k)$
(which means that
$n \in \mathcal {A}_1(k)$
(which means that
![]() $n \equiv 2 \ (\operatorname {mod}\, 4)$
), then n cannot be represented by both
$n \equiv 2 \ (\operatorname {mod}\, 4)$
), then n cannot be represented by both
![]() $x^2 + dy^2$
and
$x^2 + dy^2$
and
![]() $x^2 + \tilde d y^2$
. Since both
$x^2 + \tilde d y^2$
. Since both
![]() $d, \tilde d$
are
$d, \tilde d$
are
![]() $1 (\operatorname {mod}\, 4)$
, it follows from Lemma 3.1 (1) that
$1 (\operatorname {mod}\, 4)$
, it follows from Lemma 3.1 (1) that
![]() $R_D(n)R_{\widetilde D}(n) =0$
, and so (5.10) follows.
$R_D(n)R_{\widetilde D}(n) =0$
, and so (5.10) follows.
For the rest of the argument, we assume that
![]() $d\equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
with the goal now being to establish (5.9).
$d\equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
with the goal now being to establish (5.9).
Using (3.4), we see that
 $$ \begin{align*}\sum_{n\in {\mathcal A}_j(k)} \frac{R_D(n)R_{\widetilde D}(n)}{\tau(n^{\flat})^2} e^{-n/N} = \frac{1}{h_K h_{\widetilde K}} \sum_{\substack{\psi \in {\widehat C}_K \\ {\widetilde \psi} \in {\widehat C}_{\widetilde K}}} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi) r(n,\widetilde{\psi})}{\tau(n^{\flat})^2} e^{-n/N}. \end{align*} $$
$$ \begin{align*}\sum_{n\in {\mathcal A}_j(k)} \frac{R_D(n)R_{\widetilde D}(n)}{\tau(n^{\flat})^2} e^{-n/N} = \frac{1}{h_K h_{\widetilde K}} \sum_{\substack{\psi \in {\widehat C}_K \\ {\widetilde \psi} \in {\widehat C}_{\widetilde K}}} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi) r(n,\widetilde{\psi})}{\tau(n^{\flat})^2} e^{-n/N}. \end{align*} $$
We may now use Lemma 8.4 to estimate the contribution of all the characters
![]() $\psi $
and
$\psi $
and
![]() ${\widetilde \psi }$
apart from when (i) both
${\widetilde \psi }$
apart from when (i) both
![]() $\psi $
and
$\psi $
and
![]() ${\widetilde \psi }$
are the principal characters in their respective class groups, and (ii) both
${\widetilde \psi }$
are the principal characters in their respective class groups, and (ii) both
![]() $\psi $
and
$\psi $
and
![]() ${\widetilde \psi }$
are the nontrivial genus characters in their class groups. Note that the second case only arises when
${\widetilde \psi }$
are the nontrivial genus characters in their class groups. Note that the second case only arises when
![]() $j = 1$
, and since
$j = 1$
, and since
![]() $d \equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
, we have here (with notation as in Proposition 8.3)
$d \equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
, we have here (with notation as in Proposition 8.3)
for all n. To see this, we use Proposition 8.3 and multiplicativity of
![]() $r(n,\psi )$
to deduce that
$r(n,\psi )$
to deduce that
![]() $r(n,\psi _1) = \chi _{-4}( n) r(n,\psi _0)$
and similarly
$r(n,\psi _1) = \chi _{-4}( n) r(n,\psi _0)$
and similarly
![]() $r(n, \widetilde {\psi }_1) = \chi _{-4}(n) r(n, \widetilde {\psi }_0)$
for odd n so that the stated relation holds for n odd. Further
$r(n, \widetilde {\psi }_1) = \chi _{-4}(n) r(n, \widetilde {\psi }_0)$
for odd n so that the stated relation holds for n odd. Further
![]() $r(2^a, \psi _1) = \chi _d(2^a) r(2^a, \psi _0)$
and
$r(2^a, \psi _1) = \chi _d(2^a) r(2^a, \psi _0)$
and
![]() $r(2^a, \widetilde {\psi }_1) = \chi _{{\widetilde d}}(2^a) r(2^a, \widetilde {\psi }_0)$
, and since
$r(2^a, \widetilde {\psi }_1) = \chi _{{\widetilde d}}(2^a) r(2^a, \widetilde {\psi }_0)$
, and since
![]() $\chi _d(2) = \chi _{\widetilde d}(2)$
(because
$\chi _d(2) = \chi _{\widetilde d}(2)$
(because
![]() $d\equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
) we see the stated relation for even n as well. Thus,
$d\equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
) we see the stated relation for even n as well. Thus,
 $$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} \frac{R_D(n)R_{\widetilde D}(n)}{\tau(n^{\flat})^2} e^{-n/N} = \frac{2^j}{h_K h_{\widetilde K}} M + O\big( N (\log N)^{-100}\big), \end{align} $$
$$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} \frac{R_D(n)R_{\widetilde D}(n)}{\tau(n^{\flat})^2} e^{-n/N} = \frac{2^j}{h_K h_{\widetilde K}} M + O\big( N (\log N)^{-100}\big), \end{align} $$
where
 $$ \begin{align} M := \sum_{n\in {\mathcal A}_j(k)} \frac{r(n,\psi_0)r(n,{\widetilde \psi}_0)}{\tau(n^{\flat})^2} e^{-n/N}. \end{align} $$
$$ \begin{align} M := \sum_{n\in {\mathcal A}_j(k)} \frac{r(n,\psi_0)r(n,{\widetilde \psi}_0)}{\tau(n^{\flat})^2} e^{-n/N}. \end{align} $$
To evaluate the main term M above, we proceed analogously to the previous section using Selberg’s method. To highlight the close parallels with the earlier argument, we will use the same notation for the analogous Dirichlet series that arise here. The first step is to consider, for
![]() $|z| = 1$
, the Dirichlet series
$|z| = 1$
, the Dirichlet series
 $$ \begin{align} \mathcal{F}(s; z, j) := \sum_{v_2(n) = j } \frac{r(n,\psi_0)r(n,{\widetilde \psi}_0)}{\tau(n^{\flat})^2 } z^{\Omega(n)} n^{-s}, \end{align} $$
$$ \begin{align} \mathcal{F}(s; z, j) := \sum_{v_2(n) = j } \frac{r(n,\psi_0)r(n,{\widetilde \psi}_0)}{\tau(n^{\flat})^2 } z^{\Omega(n)} n^{-s}, \end{align} $$
which converges absolutely for
![]() $\sigma =\text {Re }(s)>1$
and defines a holomorphic function there. As in the previous section, we shall obtain an analytic continuation of
$\sigma =\text {Re }(s)>1$
and defines a holomorphic function there. As in the previous section, we shall obtain an analytic continuation of
![]() ${\mathcal F}$
to a wider region by writing
${\mathcal F}$
to a wider region by writing
Note that
![]() $\zeta (s)L(s,\chi _D) L(s,\chi _{\widetilde D}) L(s,\chi _{d\widetilde {d}})$
is the Dedekind zeta-function of the biquadratic field
$\zeta (s)L(s,\chi _D) L(s,\chi _{\widetilde D}) L(s,\chi _{d\widetilde {d}})$
is the Dedekind zeta-function of the biquadratic field
![]() $L={\mathbb Q}(\sqrt {D}, \sqrt {\widetilde D})$
, and
$L={\mathbb Q}(\sqrt {D}, \sqrt {\widetilde D})$
, and
where the logarithm is initially defined in
![]() $\sigma>1$
by an absolutely convergent Dirichlet series as in (8.2). Thus, (10.4) should be thought of as the definition of the function
$\sigma>1$
by an absolutely convergent Dirichlet series as in (8.2). Thus, (10.4) should be thought of as the definition of the function
![]() ${\mathcal G}(s;z,j)$
, which is holomorphic in the half plane
${\mathcal G}(s;z,j)$
, which is holomorphic in the half plane
![]() $\sigma>1$
. We shall see shortly that
$\sigma>1$
. We shall see shortly that
![]() ${\mathcal G}(s;z,j)$
is analytic in
${\mathcal G}(s;z,j)$
is analytic in
![]() $\sigma> \frac 12$
with suitable bounds in that region. By Lemma 8.1 (2), we may obtain an analytic continuation of
$\sigma> \frac 12$
with suitable bounds in that region. By Lemma 8.1 (2), we may obtain an analytic continuation of
![]() $\log ((s-1) \zeta (s)L(s,\chi _D) L(s,\chi _{\widetilde D}) L(s,\chi _{d\widetilde {d}}))$
to the region
$\log ((s-1) \zeta (s)L(s,\chi _D) L(s,\chi _{\widetilde D}) L(s,\chi _{d\widetilde {d}}))$
to the region
![]() ${\mathcal R}_0$
with corresponding bounds in the region
${\mathcal R}_0$
with corresponding bounds in the region
![]() ${\mathcal R}$
. In this way, we obtain a continuation of
${\mathcal R}$
. In this way, we obtain a continuation of
![]() ${\mathcal F}(s;z,j)$
essentially to the region
${\mathcal F}(s;z,j)$
essentially to the region
![]() ${\mathcal R}$
, with the caveat that the real line segment to the left of
${\mathcal R}$
, with the caveat that the real line segment to the left of
![]() $s=1$
must be omitted owing to the logarithmic singularity at
$s=1$
must be omitted owing to the logarithmic singularity at
![]() $s=1$
.
$s=1$
.
From the multiplicative definition of
![]() ${\mathcal F}(s;z,j)$
, in the region
${\mathcal F}(s;z,j)$
, in the region
![]() $\sigma> 1$
we see that
$\sigma> 1$
we see that
![]() ${\mathcal G}(s;z,j)$
is given by an Euler product
${\mathcal G}(s;z,j)$
is given by an Euler product
![]() $\prod _{p} {\mathcal G}_p(s;z,j)$
. We continue as in Section 9 by describing these Euler factors and showing that the Euler product converges absolutely in
$\prod _{p} {\mathcal G}_p(s;z,j)$
. We continue as in Section 9 by describing these Euler factors and showing that the Euler product converges absolutely in
![]() $\sigma>\frac 12$
(and assume below that
$\sigma>\frac 12$
(and assume below that
![]() $\sigma>\frac 12$
).
$\sigma>\frac 12$
).
In the case
![]() $p>W$
, we have
$p>W$
, we have
 $$\begin{align*}{\mathcal G}_p(s;z,j) &= \left( \sum_{\ell =0}^{\infty} r(p^{\ell}, \psi_0) r(p^{\ell},\widetilde{\psi_0}) z^{\ell} p^{-\ell s}\right) \big( 1-p^{-s}\big)^{z} \big( 1- \chi_D(p)p^{-s}\big)^{z} \big( 1- \chi_{\widetilde D}(p)p^{-s}\big)^z \\ &\quad \times \big( 1-\chi_{d{\widetilde d}}(p) p^{-s}\big)^z. \end{align*}$$
$$\begin{align*}{\mathcal G}_p(s;z,j) &= \left( \sum_{\ell =0}^{\infty} r(p^{\ell}, \psi_0) r(p^{\ell},\widetilde{\psi_0}) z^{\ell} p^{-\ell s}\right) \big( 1-p^{-s}\big)^{z} \big( 1- \chi_D(p)p^{-s}\big)^{z} \big( 1- \chi_{\widetilde D}(p)p^{-s}\big)^z \\ &\quad \times \big( 1-\chi_{d{\widetilde d}}(p) p^{-s}\big)^z. \end{align*}$$
Since
![]() $0\leq r(p^\ell ,\psi _0) r(p^{\ell },\widetilde {\psi _0}) \leq (\ell +1)^2$
, and
$0\leq r(p^\ell ,\psi _0) r(p^{\ell },\widetilde {\psi _0}) \leq (\ell +1)^2$
, and
![]() $r(p,\psi _0) r(p,\widetilde {\psi _0}) = (1+ \chi _D(p))(1+\chi _{\widetilde D}(p)) = 1 +\chi _D(p) + \chi _{\widetilde D}(p) + \chi _{d{\widetilde d}} (p)$
(note that for odd p, we have
$r(p,\psi _0) r(p,\widetilde {\psi _0}) = (1+ \chi _D(p))(1+\chi _{\widetilde D}(p)) = 1 +\chi _D(p) + \chi _{\widetilde D}(p) + \chi _{d{\widetilde d}} (p)$
(note that for odd p, we have
![]() $\chi _D(p) \chi _{\widetilde D}(p) = (\frac {D}{p})(\frac {\widetilde D}{p}) = (\frac {D{\widetilde D}}{p}) = (\frac {d{\widetilde d}}{p}) = \chi _{d{\widetilde d}}(p)$
), we see that
$\chi _D(p) \chi _{\widetilde D}(p) = (\frac {D}{p})(\frac {\widetilde D}{p}) = (\frac {D{\widetilde D}}{p}) = (\frac {d{\widetilde d}}{p}) = \chi _{d{\widetilde d}}(p)$
), we see that
 $$ \begin{align} {\mathcal G}_p(s;z,j) &= \big( 1 + z (1+\chi_D(p)+\chi_{\widetilde D}(p) + \chi_{d {\widetilde d}}(p)) p^{-s} + O(p^{-2\sigma}) \big) \nonumber \\ & \qquad \times \big( 1 - z (1+\chi_D(p)+\chi_{\widetilde D}(p) + \chi_{d {\widetilde d}}(p)) p^{-s} + O(p^{-2\sigma}) \big) \nonumber \\ &= 1+ O(p^{-2\sigma}). \end{align} $$
$$ \begin{align} {\mathcal G}_p(s;z,j) &= \big( 1 + z (1+\chi_D(p)+\chi_{\widetilde D}(p) + \chi_{d {\widetilde d}}(p)) p^{-s} + O(p^{-2\sigma}) \big) \nonumber \\ & \qquad \times \big( 1 - z (1+\chi_D(p)+\chi_{\widetilde D}(p) + \chi_{d {\widetilde d}}(p)) p^{-s} + O(p^{-2\sigma}) \big) \nonumber \\ &= 1+ O(p^{-2\sigma}). \end{align} $$
Turning to the case
![]() $3 \leq p \leq W$
, recall that
$3 \leq p \leq W$
, recall that
![]() $n^{\flat }$
is the product of all the prime divisors of n which are
$n^{\flat }$
is the product of all the prime divisors of n which are
![]() $\leq W$
, and recall also that
$\leq W$
, and recall also that
![]() $\chi _D(p) = \chi _{\widetilde D}(p)=1$
from the definition of
$\chi _D(p) = \chi _{\widetilde D}(p)=1$
from the definition of
![]() $\mathcal {D}_0$
,
$\mathcal {D}_0$
,
![]() $\mathcal {D}_1$
(see (5.2) and (5.3)). Thus, (as in the last section) we see that
$\mathcal {D}_1$
(see (5.2) and (5.3)). Thus, (as in the last section) we see that
 $$ \begin{align} \mathcal{G}_p(s,z,j) = \left(\sum_{\ell =0}^{\infty} z^{\ell} p^{-\ell s} \right) \big( 1-p^{-s} \big)^{4z} = \big(1 - z p^{-s} \big)^{-1} \big( 1- p^{-s}\big)^{4z}. \end{align} $$
$$ \begin{align} \mathcal{G}_p(s,z,j) = \left(\sum_{\ell =0}^{\infty} z^{\ell} p^{-\ell s} \right) \big( 1-p^{-s} \big)^{4z} = \big(1 - z p^{-s} \big)^{-1} \big( 1- p^{-s}\big)^{4z}. \end{align} $$
As in the last section, for primes
![]() $p\geq 3$
there is no difference between the cases
$p\geq 3$
there is no difference between the cases
![]() $j=0$
and
$j=0$
and
![]() $j=1$
, but at the prime
$j=1$
, but at the prime
![]() $p = 2$
, there is a distinction in the definition of
$p = 2$
, there is a distinction in the definition of
![]() ${\mathcal G}_2(s;z,j)$
. Here, we have (compare with (9.7))
${\mathcal G}_2(s;z,j)$
. Here, we have (compare with (9.7))
 $$ \begin{align} \mathcal{G}_2(s,z,j) = \begin{cases} (1-2^{-s})^{4z} &\text{if } j=0\\ z2^{-s-2} (1-2^{-s})^{2z} &\text{if } j=1, \end{cases} \end{align} $$
$$ \begin{align} \mathcal{G}_2(s,z,j) = \begin{cases} (1-2^{-s})^{4z} &\text{if } j=0\\ z2^{-s-2} (1-2^{-s})^{2z} &\text{if } j=1, \end{cases} \end{align} $$
upon noting that when
![]() $j=0$
we have
$j=0$
we have
![]() $\chi _D(2) = \chi _{\widetilde D}(2) = \chi _{d {\widetilde d}}(2)= 1$
(since D,
$\chi _D(2) = \chi _{\widetilde D}(2) = \chi _{d {\widetilde d}}(2)= 1$
(since D,
![]() ${\widetilde D}$
and
${\widetilde D}$
and
![]() $d{\widetilde d}$
are all
$d{\widetilde d}$
are all
![]() $1\ (\operatorname {mod}\, 8)$
), and that when
$1\ (\operatorname {mod}\, 8)$
), and that when
![]() $j=1$
we have
$j=1$
we have
![]() $\chi _D(2) = \chi _{\widetilde D}(2) = 0$
and
$\chi _D(2) = \chi _{\widetilde D}(2) = 0$
and
![]() $\chi _{d\widetilde d}(2) = 1$
(since
$\chi _{d\widetilde d}(2) = 1$
(since
![]() $d\equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
so that
$d\equiv {\widetilde d} \ (\operatorname {mod}\, 8)$
so that
![]() $d\widetilde d \equiv 1 \ (\operatorname {mod}\, 8)$
). From (10.6) and (10.7) note that for all
$d\widetilde d \equiv 1 \ (\operatorname {mod}\, 8)$
). From (10.6) and (10.7) note that for all
![]() $p\leq W$
$p\leq W$
From (10.5) and (10.8), we see that the Euler product
![]() $\prod _p {\mathcal G}_p(s;z,j)$
, which was known initially to converge absolutely for
$\prod _p {\mathcal G}_p(s;z,j)$
, which was known initially to converge absolutely for
![]() $\sigma>1$
, in fact converges absolutely in
$\sigma>1$
, in fact converges absolutely in
![]() $\sigma> \frac 12$
. Moreover, for
$\sigma> \frac 12$
. Moreover, for
![]() $\sigma \geq \frac 34$
we deduce that
$\sigma \geq \frac 34$
we deduce that
 $$ \begin{align} | {\mathcal G}(s;z,j)| \ll \exp\left( \sum_{p\leq W} O(p^{-3/4})\right) \ll \exp(W^{1/4}). \end{align} $$
$$ \begin{align} | {\mathcal G}(s;z,j)| \ll \exp\left( \sum_{p\leq W} O(p^{-3/4})\right) \ll \exp(W^{1/4}). \end{align} $$
By Selberg’s method, specifically by (A.7) and (A.9), we obtain
 $$ \begin{align} \sum_{ v_2(n) = j} \frac{r(n, \psi_0) r(n,{\widetilde \psi}_0)}{\tau(n^{\flat})^2} z^{\Omega(n)} e^{-n/N} & = \frac{N}{\log N} \frac{(L_{d,\tilde d} \log N)^{z}}{\Gamma(z)} {\mathcal G}(1;z,j) \nonumber \\ &\quad + O_{\varepsilon}\big( N (\log N)^{\text{Re }z -\frac 32 + \varepsilon}\big), \end{align} $$
$$ \begin{align} \sum_{ v_2(n) = j} \frac{r(n, \psi_0) r(n,{\widetilde \psi}_0)}{\tau(n^{\flat})^2} z^{\Omega(n)} e^{-n/N} & = \frac{N}{\log N} \frac{(L_{d,\tilde d} \log N)^{z}}{\Gamma(z)} {\mathcal G}(1;z,j) \nonumber \\ &\quad + O_{\varepsilon}\big( N (\log N)^{\text{Re }z -\frac 32 + \varepsilon}\big), \end{align} $$
where, here and below,
The main quantity of interest M (see (10.2)) may be recovered by Fourier inversion, integrating over
![]() $z=e^{i\theta }$
with
$z=e^{i\theta }$
with
![]() $-\pi \leq \theta \leq \pi $
. Thus, analogously to (9.11) we find
$-\pi \leq \theta \leq \pi $
. Thus, analogously to (9.11) we find
 $$ \begin{align*}M= \frac{N}{\log N} \frac{1}{2\pi} \int_{-\pi}^{\pi} (L_{d,\tilde d} \log N)^{e^{i\theta}} \frac{\mathcal G(1;e^{i\theta},j)}{\Gamma(e^{i\theta})} e^{-ik \theta} d\theta +O_{\varepsilon}\big( N (\log N)^{\varepsilon - 1/2}\big). \end{align*} $$
$$ \begin{align*}M= \frac{N}{\log N} \frac{1}{2\pi} \int_{-\pi}^{\pi} (L_{d,\tilde d} \log N)^{e^{i\theta}} \frac{\mathcal G(1;e^{i\theta},j)}{\Gamma(e^{i\theta})} e^{-ik \theta} d\theta +O_{\varepsilon}\big( N (\log N)^{\varepsilon - 1/2}\big). \end{align*} $$
Arguing as in (9.12), (9.13), (9.14), we find analogously to (9.15)
 $$ \begin{align*}\frac{{\mathcal G}(1;e^{i\theta},j)}{\Gamma(e^{i\theta})} = {\mathcal G}(1;1,j) \big( 1+ O (|\theta| (\log W)^C)\big), \end{align*} $$
$$ \begin{align*}\frac{{\mathcal G}(1;e^{i\theta},j)}{\Gamma(e^{i\theta})} = {\mathcal G}(1;1,j) \big( 1+ O (|\theta| (\log W)^C)\big), \end{align*} $$
for a suitable constant C. Using this in our expression for M and arguing as in (9.17) and (9.18) we arrive at
 $$ \begin{align} M = \frac{N}{\log N} \frac{ (\log (L_{d,\tilde d} \log N))^k}{k!} {\mathcal G}(1;1,j) +O\big( k_0^{\varepsilon - 1} N L_{d,\tilde d} \big). \end{align} $$
$$ \begin{align} M = \frac{N}{\log N} \frac{ (\log (L_{d,\tilde d} \log N))^k}{k!} {\mathcal G}(1;1,j) +O\big( k_0^{\varepsilon - 1} N L_{d,\tilde d} \big). \end{align} $$
Here, the error term
![]() $O_{\varepsilon }(N (\log N)^{-1/2 + \varepsilon })$
has been absorbed into the error term above since the L-values at
$O_{\varepsilon }(N (\log N)^{-1/2 + \varepsilon })$
has been absorbed into the error term above since the L-values at
![]() $1$
are all
$1$
are all
![]() $\gg |D|^{-\varepsilon } \gg (\log N)^{-\varepsilon }$
.
$\gg |D|^{-\varepsilon } \gg (\log N)^{-\varepsilon }$
.
Applying (9.20) with
![]() $x= L_{d,\tilde d}$
(which satisfies
$x= L_{d,\tilde d}$
(which satisfies
![]() $(\log N)^{-\varepsilon } \ll L_{d,\tilde d} \ll k_0^3$
), we see that for k in the range (5.5)
$(\log N)^{-\varepsilon } \ll L_{d,\tilde d} \ll k_0^3$
), we see that for k in the range (5.5)
 $$\begin{align*}\frac{ (\log ( L_{d,\tilde d} \log N))^k}{k!} = L_{d,\tilde d} \frac{k_0^{k}}{k!} +(\log N) O_{\varepsilon}\big( k_0^{\varepsilon - 5/6}L_{d,\tilde d} + k_0^{-3}\big). \end{align*}$$
$$\begin{align*}\frac{ (\log ( L_{d,\tilde d} \log N))^k}{k!} = L_{d,\tilde d} \frac{k_0^{k}}{k!} +(\log N) O_{\varepsilon}\big( k_0^{\varepsilon - 5/6}L_{d,\tilde d} + k_0^{-3}\big). \end{align*}$$
Using this in (10.11), we conclude that
 $$ \begin{align} M = \frac{N}{\log N} {\mathcal G}(1;1,j) L_{d,\tilde d} \frac{k_0^k }{k! } + N O_{\varepsilon}\big( k_0^{\varepsilon - 5/6} L_{d,\tilde d} + k_0^{-3} \big). \end{align} $$
$$ \begin{align} M = \frac{N}{\log N} {\mathcal G}(1;1,j) L_{d,\tilde d} \frac{k_0^k }{k! } + N O_{\varepsilon}\big( k_0^{\varepsilon - 5/6} L_{d,\tilde d} + k_0^{-3} \big). \end{align} $$
From (10.5), (10.6) and (10.7), we see that
(In fact, rather than use the crude bound (10.5) one may compute
![]() $\mathcal {G}_p(1,1,j) = 1 - \chi _{d\tilde d}(p)p^{-2}$
for
$\mathcal {G}_p(1,1,j) = 1 - \chi _{d\tilde d}(p)p^{-2}$
for
![]() $p> W$
, but we do not need this.) Using this together with the class number formula (9.22) and (10.12) in (10.1), (10.2), we obtain
$p> W$
, but we do not need this.) Using this together with the class number formula (9.22) and (10.12) in (10.1), (10.2), we obtain
 $$ \begin{align*} \sum_{n\in {\mathcal A}_j(k)} & \frac{R_D(n)R_{{\widetilde D}}(n)}{\tau(f)^2} e^{-n/N} =\big(\tfrac{1}{2} + O(W^{-1})\big) \pi^2 \gamma_W^3 |D{\widetilde D}|^{-1/2} L(1,\chi_{d\widetilde {d}}) \frac{N}{ \log N} \frac{k_0^k}{k!} \\ &+ N |D \tilde D|^{-1/2} O_{\varepsilon}\Big( k_0^{\varepsilon - 5/6} L(1,\chi_{d{\widetilde d}}) + k_0^{-3} L(1,\chi_D)^{-1} L(1,\chi_{\widetilde D})^{-1}\Big), \end{align*} $$
$$ \begin{align*} \sum_{n\in {\mathcal A}_j(k)} & \frac{R_D(n)R_{{\widetilde D}}(n)}{\tau(f)^2} e^{-n/N} =\big(\tfrac{1}{2} + O(W^{-1})\big) \pi^2 \gamma_W^3 |D{\widetilde D}|^{-1/2} L(1,\chi_{d\widetilde {d}}) \frac{N}{ \log N} \frac{k_0^k}{k!} \\ &+ N |D \tilde D|^{-1/2} O_{\varepsilon}\Big( k_0^{\varepsilon - 5/6} L(1,\chi_{d{\widetilde d}}) + k_0^{-3} L(1,\chi_D)^{-1} L(1,\chi_{\widetilde D})^{-1}\Big), \end{align*} $$
where we have absorbed the error term
![]() $O(N(\log N)^{-100})$
from (10.1) into the much larger error term above.
$O(N(\log N)^{-100})$
from (10.1) into the much larger error term above.
To complete the proof of Proposition 5.3, we multiply though by
![]() $|D \tilde D|^{1/2} /\pi ^2 \gamma _W^2$
(noting that any extraneous factors of
$|D \tilde D|^{1/2} /\pi ^2 \gamma _W^2$
(noting that any extraneous factors of
![]() $\gamma _W$
may be absorbed by
$\gamma _W$
may be absorbed by
![]() $k_0^{\varepsilon }$
terms) and, finally, use (5.8).
$k_0^{\varepsilon }$
terms) and, finally, use (5.8).
11 Proof of Proposition 5.4
In this final section of the main paper, we establish Proposition 5.4.
Using (3.4), we see that
 $$ \begin{align*}\sum_{n\in {\mathcal A}_j(k)} \frac{R_D(n)^2}{\tau(n^{\flat})^2} e^{-n/N} = \frac{1}{h_K^2} \sum_{\psi, \widetilde{\psi} \in {\widehat C}_K} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi) r(n,\widetilde{\psi})}{\tau(n^{\flat})^2} e^{-n/N}. \end{align*} $$
$$ \begin{align*}\sum_{n\in {\mathcal A}_j(k)} \frac{R_D(n)^2}{\tau(n^{\flat})^2} e^{-n/N} = \frac{1}{h_K^2} \sum_{\psi, \widetilde{\psi} \in {\widehat C}_K} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi) r(n,\widetilde{\psi})}{\tau(n^{\flat})^2} e^{-n/N}. \end{align*} $$
Using Lemma 8.5, we may bound the contribution of terms with
![]() ${\widetilde \psi } \notin \{ \psi , \overline {\psi }\}$
by
${\widetilde \psi } \notin \{ \psi , \overline {\psi }\}$
by
![]() $\ll N(\log N)^{-100}$
. It remains to treat the cases when
$\ll N(\log N)^{-100}$
. It remains to treat the cases when
![]() ${\widetilde \psi } = \psi $
or
${\widetilde \psi } = \psi $
or
![]() $\overline {\psi }$
. Note that if
$\overline {\psi }$
. Note that if
![]() ${\mathfrak a}$
is an ideal of norm n, then so is
${\mathfrak a}$
is an ideal of norm n, then so is
![]() $\overline {\mathfrak a}$
and moreover
$\overline {\mathfrak a}$
and moreover
![]() $(n)={\mathfrak a} \overline {\mathfrak a}$
. Therefore,
$(n)={\mathfrak a} \overline {\mathfrak a}$
. Therefore,
![]() $\overline \psi ({\mathfrak a}) = {\psi }(\overline {\mathfrak a})$
and it follows that
$\overline \psi ({\mathfrak a}) = {\psi }(\overline {\mathfrak a})$
and it follows that
![]() $r(n,\psi ) = r(n, \overline {\psi })$
is real valued. Thus, when
$r(n,\psi ) = r(n, \overline {\psi })$
is real valued. Thus, when
![]() $\widetilde \psi $
is
$\widetilde \psi $
is
![]() $\psi $
or
$\psi $
or
![]() ${\overline \psi }$
we have
${\overline \psi }$
we have
![]() $r(n,\psi ) r(n, {\widetilde \psi }) = r(n,\psi )^2$
, which is real and nonnegative. Collecting the observations so far, we find
$r(n,\psi ) r(n, {\widetilde \psi }) = r(n,\psi )^2$
, which is real and nonnegative. Collecting the observations so far, we find
 $$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} \frac{R_D(n)^2}{\tau(n^{\flat})^2} e^{-n/N} \ll \frac{1}{h_K^2} \sum_{\psi \in {\widehat C}_K} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi)^2}{\tau(n^{\flat})^2} e^{-n/N} + N (\log N)^{-100}. \end{align} $$
$$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} \frac{R_D(n)^2}{\tau(n^{\flat})^2} e^{-n/N} \ll \frac{1}{h_K^2} \sum_{\psi \in {\widehat C}_K} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi)^2}{\tau(n^{\flat})^2} e^{-n/N} + N (\log N)^{-100}. \end{align} $$
The contribution of the real characters
![]() $\psi $
(which are the genus characters, and there are at most two of them) to (11.1) is
$\psi $
(which are the genus characters, and there are at most two of them) to (11.1) is
 $$ \begin{align*}\ll \frac{1}{h_K^2} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi_0)^2}{\tau(n^{\flat})^2} e^{-n/N} \ll \frac{2^k}{h_K^2} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi_0)}{\tau(n^{\flat})} e^{-n/N} \end{align*} $$
$$ \begin{align*}\ll \frac{1}{h_K^2} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi_0)^2}{\tau(n^{\flat})^2} e^{-n/N} \ll \frac{2^k}{h_K^2} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi_0)}{\tau(n^{\flat})} e^{-n/N} \end{align*} $$
since
![]() $r(n,\psi _0) \leq 2^{\Omega (n)} \leq 2^k$
. Using (9.1) and Proposition 5.2, the above quantity is bounded by
$r(n,\psi _0) \leq 2^{\Omega (n)} \leq 2^k$
. Using (9.1) and Proposition 5.2, the above quantity is bounded by
 $$\begin{align*}\ll_{\varepsilon} \frac{2^k}{h_K} \frac{\gamma_W}{|D|^{1/2}} \left(\sum_{n \in \mathcal{A}_j(k)} e^{-n/N} + k_0^{\varepsilon - 5/6} N + k_0^{-2} L(1,\chi_D)^{-1} N \right). \end{align*}$$
$$\begin{align*}\ll_{\varepsilon} \frac{2^k}{h_K} \frac{\gamma_W}{|D|^{1/2}} \left(\sum_{n \in \mathcal{A}_j(k)} e^{-n/N} + k_0^{\varepsilon - 5/6} N + k_0^{-2} L(1,\chi_D)^{-1} N \right). \end{align*}$$
By (5.8) and Stirling’s formula, this is
 $$ \begin{align} \ll N \frac{2^k}{h_K} \frac{\gamma_W}{|D|^{1/2}} \big(k_0^{-1/2} + k_0^{-2} L(1,\chi_D)^{-1} \big). \end{align} $$
$$ \begin{align} \ll N \frac{2^k}{h_K} \frac{\gamma_W}{|D|^{1/2}} \big(k_0^{-1/2} + k_0^{-2} L(1,\chi_D)^{-1} \big). \end{align} $$
Now, we bound the contribution of the complex characters
![]() $\psi $
in (11.1). For a complex character
$\psi $
in (11.1). For a complex character
![]() $\psi $
, note that
$\psi $
, note that
 $$ \begin{align} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi)^2}{\tau(n^{\flat})^2} e^{-n/N} \leq \sum_{n} r(n,\psi)^2 e^{-n/N} = \frac{1}{2\pi i} \int_{c-i\infty}^{c+i\infty} \sum_{n=1}^{\infty} \frac{r(n,\psi)^2}{n^s} N^s \Gamma(s) ds, \end{align} $$
$$ \begin{align} \sum_{n \in {\mathcal A}_j(k)} \frac{r(n,\psi)^2}{\tau(n^{\flat})^2} e^{-n/N} \leq \sum_{n} r(n,\psi)^2 e^{-n/N} = \frac{1}{2\pi i} \int_{c-i\infty}^{c+i\infty} \sum_{n=1}^{\infty} \frac{r(n,\psi)^2}{n^s} N^s \Gamma(s) ds, \end{align} $$
where we take
![]() $c= 1+ 1/\log N$
. By considering whether p does or does not split in
$c= 1+ 1/\log N$
. By considering whether p does or does not split in
![]() $\mathbf {Q}(\sqrt {D})$
, we may check that for any unramified prime p
$\mathbf {Q}(\sqrt {D})$
, we may check that for any unramified prime p
 $$ \begin{align*}r(p,\psi)^2 = 1 + \chi_D(p) + \sum_{N(\mathfrak p) =p} \psi^2({\mathfrak p}). \end{align*} $$
$$ \begin{align*}r(p,\psi)^2 = 1 + \chi_D(p) + \sum_{N(\mathfrak p) =p} \psi^2({\mathfrak p}). \end{align*} $$
Since
![]() $\psi $
is not real, note that
$\psi $
is not real, note that
![]() $\psi ^2$
is not principal. By comparing Euler products, we may therefore write
$\psi ^2$
is not principal. By comparing Euler products, we may therefore write
 $$ \begin{align*}\sum_{n=1}^{\infty} \frac{r(n,\psi)^2}{n^s} = \zeta(s) L(s,\chi_D) L(s,\psi^2) {\mathcal G}(s), \end{align*} $$
$$ \begin{align*}\sum_{n=1}^{\infty} \frac{r(n,\psi)^2}{n^s} = \zeta(s) L(s,\chi_D) L(s,\psi^2) {\mathcal G}(s), \end{align*} $$
where
![]() ${\mathcal G}(s)$
is given by an Euler product which converges absolutely in the region
${\mathcal G}(s)$
is given by an Euler product which converges absolutely in the region
![]() ${\operatorname {Re}} s> \tfrac 12+ \delta $
and is uniformly bounded in that region. Moving the line of integration in (11.3) to the line
${\operatorname {Re}} s> \tfrac 12+ \delta $
and is uniformly bounded in that region. Moving the line of integration in (11.3) to the line
![]() ${\operatorname {Re}} s=\frac {3}{4}$
, we see that this integral equals
${\operatorname {Re}} s=\frac {3}{4}$
, we see that this integral equals
 $$ \begin{align} NL(1,\chi_D) L(1,\psi^2) {\mathcal G}(1) + \frac{1}{2\pi i} \int^{3/4 + i \infty}_{3/4 - i \infty} \zeta(s) L(s,\chi_D) L(s,\psi^2) {\mathcal G}(s) N^s \Gamma(s) ds. \end{align} $$
$$ \begin{align} NL(1,\chi_D) L(1,\psi^2) {\mathcal G}(1) + \frac{1}{2\pi i} \int^{3/4 + i \infty}_{3/4 - i \infty} \zeta(s) L(s,\chi_D) L(s,\psi^2) {\mathcal G}(s) N^s \Gamma(s) ds. \end{align} $$
To bound the integral above, we use the convexity bound for L-functions (see Chapter 5 of [Reference Iwaniec and Kowalski13], as well as (8.4) in the case of
![]() $L(s,\psi ^2)$
) which gives
$L(s,\psi ^2)$
) which gives
and
Noting further that
![]() $|{\mathcal G}(\frac 34+it)| \ll 1$
, and
$|{\mathcal G}(\frac 34+it)| \ll 1$
, and
![]() $|\Gamma (\frac 34+it)| \ll (1+|t|)^{1/4} e^{-\pi |t|/2}$
(see (C.19) of [Reference Montgomery and Vaughan14]), we may bound the integral on
$|\Gamma (\frac 34+it)| \ll (1+|t|)^{1/4} e^{-\pi |t|/2}$
(see (C.19) of [Reference Montgomery and Vaughan14]), we may bound the integral on
![]() ${\operatorname {Re}} s =\frac {3}{4}$
in (11.4) by
${\operatorname {Re}} s =\frac {3}{4}$
in (11.4) by
 $$\begin{align*}\ll_{\varepsilon} N^{3/4}\int^{\infty}_{-\infty} |D|^{1/4+\varepsilon} (1+|t|) e^{-\pi |t|/2} dt \ll N^{3/4} |D|^{1/2}. \end{align*}$$
$$\begin{align*}\ll_{\varepsilon} N^{3/4}\int^{\infty}_{-\infty} |D|^{1/4+\varepsilon} (1+|t|) e^{-\pi |t|/2} dt \ll N^{3/4} |D|^{1/2}. \end{align*}$$
With this in mind, and referring back to (11.3), (11.4), it follows that for complex
![]() $\psi $
we have
$\psi $
we have
 $$\begin{align*}\sum_{n \in \mathcal{A}_j(k)} \frac{r(n, \psi)^2}{\tau(n^{\flat})^2} e^{-n/N} \ll N L(1,\chi_D) L(1, \psi^2) + N^{3/4} |D|^{1/2} .\end{align*}$$
$$\begin{align*}\sum_{n \in \mathcal{A}_j(k)} \frac{r(n, \psi)^2}{\tau(n^{\flat})^2} e^{-n/N} \ll N L(1,\chi_D) L(1, \psi^2) + N^{3/4} |D|^{1/2} .\end{align*}$$
Now,
![]() $L(1,\psi ^2) \ll (\log |D|)^2$
by (8.4), and so we conclude that
$L(1,\psi ^2) \ll (\log |D|)^2$
by (8.4), and so we conclude that
 $$\begin{align*}\sum_{n \in \mathcal{A}_j(k)} \frac{r(n, \psi)^2}{\tau(n^{\flat})^2} e^{-n/N} \ll N L(1, \chi_D) (\log |D|)^2 + N^{3/4} |D|^{1/2} \ll N L(1,\chi_D) (\log |D|)^2, \end{align*}$$
$$\begin{align*}\sum_{n \in \mathcal{A}_j(k)} \frac{r(n, \psi)^2}{\tau(n^{\flat})^2} e^{-n/N} \ll N L(1, \chi_D) (\log |D|)^2 + N^{3/4} |D|^{1/2} \ll N L(1,\chi_D) (\log |D|)^2, \end{align*}$$
where the last estimate follows since
![]() $|D| \ll \log N$
and
$|D| \ll \log N$
and
![]() $L(1,\chi _D) \gg |D|^{-\varepsilon }$
.
$L(1,\chi _D) \gg |D|^{-\varepsilon }$
.
Thus, the contribution of the complex characters
![]() $\psi $
to (11.1) is
$\psi $
to (11.1) is
Combining this with the contribution of the real characters given in (11.2), we conclude that
 $$ \begin{align*}\sum_{n \in {\mathcal A}_j(k)} \frac{R_D(n)^2}{\tau(n^{\flat})^2}e^{-n/N} \ll N \frac{2^k}{h_K} \frac{\gamma_W}{|D|^{1/2}} \big( k_0^{-1/2} + k_0^{-2} L(1,\chi_D)^{-1} \big) + N |D|^{-1/2} (\log |D|)^2. \end{align*} $$
$$ \begin{align*}\sum_{n \in {\mathcal A}_j(k)} \frac{R_D(n)^2}{\tau(n^{\flat})^2}e^{-n/N} \ll N \frac{2^k}{h_K} \frac{\gamma_W}{|D|^{1/2}} \big( k_0^{-1/2} + k_0^{-2} L(1,\chi_D)^{-1} \big) + N |D|^{-1/2} (\log |D|)^2. \end{align*} $$
Proposition 5.4 follows upon multiplying through by
![]() $|D|/\pi ^2 \gamma _W^2$
and using the class number formula together with the trivial bound
$|D|/\pi ^2 \gamma _W^2$
and using the class number formula together with the trivial bound
![]() $\gamma _W^{-2} \ll \log |D|$
.
$\gamma _W^{-2} \ll \log |D|$
.
A Details of Selberg’s method
In this appendix, we supply proofs of the applications of Selberg’s method as used in Sections 9 and 10; namely, the asymptotic formulae (9.10) and (10.10). Let
![]() ${\mathcal F}(s;z,j)$
be defined either as in (9.2) or (10.3), and correspondingly let
${\mathcal F}(s;z,j)$
be defined either as in (9.2) or (10.3), and correspondingly let
![]() ${\mathcal G}(s;z,j)$
be defined as in (9.3) or (10.4). Define
${\mathcal G}(s;z,j)$
be defined as in (9.3) or (10.4). Define
![]() $f(n)$
to be
$f(n)$
to be
![]() $r(n,\psi _0)/\tau (n^{\flat })$
in the situation of Section 9, and
$r(n,\psi _0)/\tau (n^{\flat })$
in the situation of Section 9, and
![]() $f(n)$
to be
$f(n)$
to be
![]() $r(n,\psi _0) r(n,\widetilde {\psi _0})/\tau (n^{\flat })^2$
in the situation of Section 10. Our goal is to obtain the stated asymptotic formulae for
$r(n,\psi _0) r(n,\widetilde {\psi _0})/\tau (n^{\flat })^2$
in the situation of Section 10. Our goal is to obtain the stated asymptotic formulae for
 $$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} f(n) z^{\Omega(n)} e^{-n/N} = \frac{1}{2\pi i} \int_{c-i\infty}^{c+i\infty} {\mathcal F}(s;z,j) \Gamma(s) N^s ds, \end{align} $$
$$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} f(n) z^{\Omega(n)} e^{-n/N} = \frac{1}{2\pi i} \int_{c-i\infty}^{c+i\infty} {\mathcal F}(s;z,j) \Gamma(s) N^s ds, \end{align} $$
where we take
![]() $c = 1 +1/\log N$
.
$c = 1 +1/\log N$
.
We begin by truncating the integral in (A.1) to
![]() $|{\operatorname {Im}} s| \leq (\log \log N)^2$
. Note that in both situations under consideration
$|{\operatorname {Im}} s| \leq (\log \log N)^2$
. Note that in both situations under consideration
![]() $f(n)$
is nonnegative and bounded by
$f(n)$
is nonnegative and bounded by
![]() $\tau (n)^2$
so that
$\tau (n)^2$
so that
 $$ \begin{align*}|{\mathcal F}(c+it;z,j)| \leq \sum_{n=1}^{\infty}\tau(n)^2 n^{-c} \ll \prod_{p} \big( 1 + 4p^{-c} + O(p^{-2})\big) \ll (\log N)^4. \end{align*} $$
$$ \begin{align*}|{\mathcal F}(c+it;z,j)| \leq \sum_{n=1}^{\infty}\tau(n)^2 n^{-c} \ll \prod_{p} \big( 1 + 4p^{-c} + O(p^{-2})\big) \ll (\log N)^4. \end{align*} $$
Since
![]() $|\Gamma (c+it)| \ll (1+|t|)^{c-1/2} e^{-\pi |t|/2}$
by Stirling’s formula, we deduce that the tails of the integral in (A.1) contribute
$|\Gamma (c+it)| \ll (1+|t|)^{c-1/2} e^{-\pi |t|/2}$
by Stirling’s formula, we deduce that the tails of the integral in (A.1) contribute
 $$ \begin{align*}\int_{|t| \geq (\log \log N)^2} N^c (\log N)^4 (1+|t|)^{c-1/2} e^{-\pi |t|/2} dt \ll N (\log N)^{-100}. \end{align*} $$
$$ \begin{align*}\int_{|t| \geq (\log \log N)^2} N^c (\log N)^4 (1+|t|)^{c-1/2} e^{-\pi |t|/2} dt \ll N (\log N)^{-100}. \end{align*} $$
Thus,
 $$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} f(n) z^{\Omega(n)} e^{-n/N} = \frac{1}{2\pi i} \int_{c-i(\log \log N)^2}^{c+i (\log \log N)^2} {\mathcal F}(s;z,j) \Gamma(s) N^s ds + O\big( N (\log N)^{-100}\big), \end{align} $$
$$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} f(n) z^{\Omega(n)} e^{-n/N} = \frac{1}{2\pi i} \int_{c-i(\log \log N)^2}^{c+i (\log \log N)^2} {\mathcal F}(s;z,j) \Gamma(s) N^s ds + O\big( N (\log N)^{-100}\big), \end{align} $$
and note that the error term above is negligible compared to the error terms in the formulae (9.10) and (10.10) that we are seeking to establish.
To proceed further with evaluating the truncated integral in (A.2), we will shift contours using a Hankel or a keyhole-type contour. As in (8.10), denote by
![]() ${\mathcal W}$
the region
${\mathcal W}$
the region
and let
![]() ${\mathcal W}_*$
denote the domain
${\mathcal W}_*$
denote the domain
![]() ${\mathcal W}$
with the line segment from
${\mathcal W}$
with the line segment from
![]() $1-2 (\log N)^{-1/2}$
to
$1-2 (\log N)^{-1/2}$
to
![]() $1$
excised. In the region
$1$
excised. In the region
![]() ${\mathcal W}_*$
, we define
${\mathcal W}_*$
, we define
![]() $\log (s-1)$
to be the principal branch of the logarithm, taking real values for
$\log (s-1)$
to be the principal branch of the logarithm, taking real values for
![]() $s\in (1,\infty ]$
and if s lies just above the cut, then the argument is
$s\in (1,\infty ]$
and if s lies just above the cut, then the argument is
![]() $i\pi $
, while if s lies just below the cut, then the argument is
$i\pi $
, while if s lies just below the cut, then the argument is
![]() $-i\pi $
. This gives a definition of
$-i\pi $
. This gives a definition of
![]() $(s-1)^{w} = \exp (w \log (s-1))$
(for any complex number w), which is holomorphic in
$(s-1)^{w} = \exp (w \log (s-1))$
(for any complex number w), which is holomorphic in
![]() ${\mathcal W}_*$
. Now, as in (9.3) or (10.4), we may write
${\mathcal W}_*$
. Now, as in (9.3) or (10.4), we may write
![]() ${\mathcal F}(s;z,j) = \zeta _K(s)^z {\mathcal G}(s;z,j)$
, where K is either a quadratic (in the case of Section 9) or a biquadratic (in the case of Section 10) field. Here,
${\mathcal F}(s;z,j) = \zeta _K(s)^z {\mathcal G}(s;z,j)$
, where K is either a quadratic (in the case of Section 9) or a biquadratic (in the case of Section 10) field. Here,
![]() ${\mathcal G}(s;z,j)$
extends to a holomorphic function in a region containing
${\mathcal G}(s;z,j)$
extends to a holomorphic function in a region containing
![]() ${\mathcal W}$
, and throughout
${\mathcal W}$
, and throughout
![]() ${\mathcal W}$
it satisfies the bound
${\mathcal W}$
it satisfies the bound
![]() $|{\mathcal G}(s;z,j)| \ll \exp (W^{1/4})$
(see (9.9) or (10.9)). From Lemma 8.1 (2), we see that
$|{\mathcal G}(s;z,j)| \ll \exp (W^{1/4})$
(see (9.9) or (10.9)). From Lemma 8.1 (2), we see that
![]() $\zeta (s)^{z}$
extends to a holomorphic function on
$\zeta (s)^{z}$
extends to a holomorphic function on
![]() ${\mathcal W}_*$
, and for
${\mathcal W}_*$
, and for
![]() $s \in {\mathcal W}_*$
with
$s \in {\mathcal W}_*$
with
![]() $|{\operatorname {Im}}(s)| \geq 1$
we have
$|{\operatorname {Im}}(s)| \geq 1$
we have
where we used (8.5) together with
![]() $|D_K| \ll \Delta ^4 \leq (\log N)^4$
. Finally, again by the second part of Lemma 8.1, we see that
$|D_K| \ll \Delta ^4 \leq (\log N)^4$
. Finally, again by the second part of Lemma 8.1, we see that
![]() $((s-1) \zeta _K(s))^z$
extends to a holomorphic function in
$((s-1) \zeta _K(s))^z$
extends to a holomorphic function in
![]() ${\mathcal W}$
, and satisfies for
${\mathcal W}$
, and satisfies for
![]() $s\in {\mathcal W}$
with
$s\in {\mathcal W}$
with
![]() $|{\operatorname {Im}}(s)|\leq 1$
$|{\operatorname {Im}}(s)|\leq 1$
Synthesizing the remarks above, we conclude that
![]() ${\mathcal F}(s;z,j)$
extends holomorphically to
${\mathcal F}(s;z,j)$
extends holomorphically to
![]() ${\mathcal W}_*$
, and for
${\mathcal W}_*$
, and for
![]() $s\in {\mathcal W}_*$
with
$s\in {\mathcal W}_*$
with
![]() $|{\operatorname {Im}}(s)| \geq 1$
satisfies
$|{\operatorname {Im}}(s)| \geq 1$
satisfies
Moreover,
![]() $(s-1)^z {\mathcal F}(s;z,j)$
extends holomorphically to
$(s-1)^z {\mathcal F}(s;z,j)$
extends holomorphically to
![]() ${\mathcal W}$
, and for
${\mathcal W}$
, and for
![]() $s\in {\mathcal W}$
with
$s\in {\mathcal W}$
with
![]() $|{\operatorname {Im}} (s)|\leq 1$
satisfies
$|{\operatorname {Im}} (s)|\leq 1$
satisfies
We return now to the truncated integral in (A.2), which we will replace with an integral over the following Hankel-type contour.
This consists of
-
•
 $\Gamma _1$
, the horizontal line segment from
$\Gamma _1$
, the horizontal line segment from
 $c - i (\log \log N)^2$
to
$c - i (\log \log N)^2$
to
 $1 - (\log N)^{-1/2} - i(\log \log N)^2$
;
$1 - (\log N)^{-1/2} - i(\log \log N)^2$
; -
•
 $\Gamma _2$
, the vertical line segment from
$\Gamma _2$
, the vertical line segment from
 $1 - (\log N)^{-1/2} - i(\log \log N)^2$
to
$1 - (\log N)^{-1/2} - i(\log \log N)^2$
to
 $1 - (\log N)^{-1/2} $
;
$1 - (\log N)^{-1/2} $
; -
•
 $\Gamma _3$
, which consists of a path
$\Gamma _3$
, which consists of a path
 $\Gamma _3^-$
going horizontally from
$\Gamma _3^-$
going horizontally from
 $1-(\log N)^{-1/2}$
to
$1-(\log N)^{-1/2}$
to
 $1-r$
staying just below the line
$1-r$
staying just below the line
 ${\operatorname {Im}} s = 0$
, then a circle
${\operatorname {Im}} s = 0$
, then a circle
 $\Gamma _3^{\circ }$
of radius r about
$\Gamma _3^{\circ }$
of radius r about
 $s = 1$
, then a horizontal path
$s = 1$
, then a horizontal path
 $\Gamma _3^+$
from
$\Gamma _3^+$
from
 $1-r$
back to
$1-r$
back to
 $1 - (\log N)^{-1/2}$
but now staying just above the line
$1 - (\log N)^{-1/2}$
but now staying just above the line
 ${\operatorname {Im}} s=0$
(here
${\operatorname {Im}} s=0$
(here
 $r\leq 1/\log N$
is a parameter which we later allow to tend to
$r\leq 1/\log N$
is a parameter which we later allow to tend to
 $0$
);
$0$
); -
•
 $\Gamma _4$
, the vertical line segment from
$\Gamma _4$
, the vertical line segment from
 $1 - (\log N)^{-1/2}$
to
$1 - (\log N)^{-1/2}$
to
 $1 - (\log N)^{-1/2} + i(\log \log N)^2$
;
$1 - (\log N)^{-1/2} + i(\log \log N)^2$
; -
•
 $\Gamma _5$
, the horizontal line segment from
$\Gamma _5$
, the horizontal line segment from
 $1 - (\log N)^{-1/2} + i(\log \log N)^2$
to
$1 - (\log N)^{-1/2} + i(\log \log N)^2$
to
 $c + i (\log \log N)^2$
.
$c + i (\log \log N)^2$
.
Since the integrand
![]() ${\mathcal F}(s;z,j) \Gamma (s)N^s$
is holomorphic in
${\mathcal F}(s;z,j) \Gamma (s)N^s$
is holomorphic in
![]() ${\mathcal W}_*$
, we may replace the vertical contour from
${\mathcal W}_*$
, we may replace the vertical contour from
![]() $c - i (\log \log N)^{1/2}$
to
$c - i (\log \log N)^{1/2}$
to
![]() $c + i(\log \log N)^2$
by the Hankel-type contour
$c + i(\log \log N)^2$
by the Hankel-type contour
![]() $\Gamma _1 \cup \Gamma _2 \cup \Gamma _3 \cup \Gamma _4 \cup \Gamma _5$
.
$\Gamma _1 \cup \Gamma _2 \cup \Gamma _3 \cup \Gamma _4 \cup \Gamma _5$
.
(Note that a limiting argument, which we suppress, is required to deal with the fact that
![]() $\Gamma _3^{\pm }$
lie on the boundary of
$\Gamma _3^{\pm }$
lie on the boundary of
![]() $\mathcal {W}_*$
rather than within
$\mathcal {W}_*$
rather than within
![]() $\mathcal {W}_*$
itself.) Denote, for
$\mathcal {W}_*$
itself.) Denote, for
![]() $\ell = 1,2,3,4,5$
,
$\ell = 1,2,3,4,5$
,
 $$\begin{align*}I_\ell := \frac{1}{2\pi i} \int_{\Gamma_\ell} {\mathcal F}(s;z,j)N^s \Gamma(s) ds. \end{align*}$$
$$\begin{align*}I_\ell := \frac{1}{2\pi i} \int_{\Gamma_\ell} {\mathcal F}(s;z,j)N^s \Gamma(s) ds. \end{align*}$$
To estimate the horizontal integrals
![]() $I_1$
and
$I_1$
and
![]() $I_5$
, we use (A.3) together with the exponential decay of
$I_5$
, we use (A.3) together with the exponential decay of
![]() $|\Gamma (s)|$
. Thus, we obtain
$|\Gamma (s)|$
. Thus, we obtain
 $$\begin{align*}I_1, I_5 \ll \int_{1-(\log N)^{-1/2}}^c N^{\sigma} (\log N)^{\varepsilon} e^{-(\log \log N)^2} d\sigma \ll N (\log N)^{-100}. \end{align*}$$
$$\begin{align*}I_1, I_5 \ll \int_{1-(\log N)^{-1/2}}^c N^{\sigma} (\log N)^{\varepsilon} e^{-(\log \log N)^2} d\sigma \ll N (\log N)^{-100}. \end{align*}$$
The vertical integrals
![]() $I_2$
and
$I_2$
and
![]() $I_4$
are likewise easy to handle. If
$I_4$
are likewise easy to handle. If
![]() $|t| \geq 1$
, then (A.3) gives
$|t| \geq 1$
, then (A.3) gives
![]() $|{\mathcal F}(1-(\log N)^{-1/2}+it;z,j)| \ll (\log N)^{\varepsilon }$
, while if
$|{\mathcal F}(1-(\log N)^{-1/2}+it;z,j)| \ll (\log N)^{\varepsilon }$
, while if
![]() $|t| \leq 1$
, then from (A.4) we deduce that
$|t| \leq 1$
, then from (A.4) we deduce that
![]() $|{\mathcal F}(1-(\log N)^{-1/2}+it;z,j)| \ll (\log N)^{1/2+ \varepsilon }$
(here we take t to be either strictly positive or strictly negative but avoiding point
$|{\mathcal F}(1-(\log N)^{-1/2}+it;z,j)| \ll (\log N)^{1/2+ \varepsilon }$
(here we take t to be either strictly positive or strictly negative but avoiding point
![]() $t=0$
). Combining these estimates with the bound
$t=0$
). Combining these estimates with the bound
![]() $|\Gamma (1-(\log N)^{-1/2} + it)| \ll e^{-|t|}$
, we obtain
$|\Gamma (1-(\log N)^{-1/2} + it)| \ll e^{-|t|}$
, we obtain
 $$\begin{align*}I_2, I_4 \ll \int_{0}^{(\log \log N)^2} N^{1-(\log N)^{-1/2}} (\log N)^{1/2+\varepsilon} e^{-|t|} dt \ll N (\log N)^{-100}. \end{align*}$$
$$\begin{align*}I_2, I_4 \ll \int_{0}^{(\log \log N)^2} N^{1-(\log N)^{-1/2}} (\log N)^{1/2+\varepsilon} e^{-|t|} dt \ll N (\log N)^{-100}. \end{align*}$$
It remains lastly to consider the integral
![]() $I_3$
over the Hankel contour
$I_3$
over the Hankel contour
![]() $\Gamma _3$
. Set
$\Gamma _3$
. Set
Consider the circle centered at
![]() $1$
with radius
$1$
with radius
![]() $2(\log N)^{-1/2}$
. Since
$2(\log N)^{-1/2}$
. Since
![]() $|\Gamma (s)|$
is bounded in this region, from (A.4) we see that
$|\Gamma (s)|$
is bounded in this region, from (A.4) we see that
![]() $|{\mathcal H}(s;z,j)| \ll (\log N)^{\varepsilon }$
. Therefore, if s is any point within a circle of radius
$|{\mathcal H}(s;z,j)| \ll (\log N)^{\varepsilon }$
. Therefore, if s is any point within a circle of radius
![]() $(\log N)^{-1/2}$
centered at
$(\log N)^{-1/2}$
centered at
![]() $1$
, we see that
$1$
, we see that
 $$ \begin{align*} {\mathcal H} (s;z,j) - {\mathcal H}(1;z,j) &= \frac{1}{2\pi i} \int_{|w-1| = 2(\log N)^{-1/2}} {\mathcal H}(w;z,j) \Big( \frac{1}{w-1} - \frac{1}{w-s}\Big) dw \nonumber \\ & \ll \int_{|w-1| = 2(\log N)^{-1/2}} |{\mathcal H}(w;z,j)| \frac{|s-1|}{|(w-1)(w-s)|} |dw|\nonumber \\ & \ll (\log N)^{1/2 + \varepsilon} |s-1| , \end{align*} $$
$$ \begin{align*} {\mathcal H} (s;z,j) - {\mathcal H}(1;z,j) &= \frac{1}{2\pi i} \int_{|w-1| = 2(\log N)^{-1/2}} {\mathcal H}(w;z,j) \Big( \frac{1}{w-1} - \frac{1}{w-s}\Big) dw \nonumber \\ & \ll \int_{|w-1| = 2(\log N)^{-1/2}} |{\mathcal H}(w;z,j)| \frac{|s-1|}{|(w-1)(w-s)|} |dw|\nonumber \\ & \ll (\log N)^{1/2 + \varepsilon} |s-1| , \end{align*} $$
where we have used Cauchy’s formula and the fact that
![]() $|w-s|$
and
$|w-s|$
and
![]() $|w-1|$
are
$|w-1|$
are
![]() $\gg (\log N)^{-1/2}$
. Thus,
$\gg (\log N)^{-1/2}$
. Thus,
 $$ \begin{align} I_3 &=\frac{1}{2\pi i} \int_{\Gamma_3} (s-1)^{-z} N^s {\mathcal H}(s;z,j) ds \nonumber \\ &= \frac{1}{2\pi i} \int_{\Gamma_3} (s-1)^{-z} N^s \Big( {\mathcal H}(1;z,j) +O\big( |s-1| (\log N)^{1/2+\varepsilon}\big)\Big) ds. \end{align} $$
$$ \begin{align} I_3 &=\frac{1}{2\pi i} \int_{\Gamma_3} (s-1)^{-z} N^s {\mathcal H}(s;z,j) ds \nonumber \\ &= \frac{1}{2\pi i} \int_{\Gamma_3} (s-1)^{-z} N^s \Big( {\mathcal H}(1;z,j) +O\big( |s-1| (\log N)^{1/2+\varepsilon}\big)\Big) ds. \end{align} $$
Consider first the error term in (A.5). On the two horizontal parts of
![]() $\Gamma _3$
, namely
$\Gamma _3$
, namely
![]() $s= \sigma + 0^{\pm } i$
(depending whether we are just above or just below the cut), we have
$s= \sigma + 0^{\pm } i$
(depending whether we are just above or just below the cut), we have
![]() $|(s-1)^{-z}N^s| \ll (1-\sigma )^{-{\operatorname {Re}} z} N^{\sigma }$
so that these integrals contribute
$|(s-1)^{-z}N^s| \ll (1-\sigma )^{-{\operatorname {Re}} z} N^{\sigma }$
so that these integrals contribute
 $$ \begin{align*}\ll (\log N)^{1/2 +\varepsilon} \int_{1-(\log N)^{-1/2}}^{1-r} (1-\sigma)^{1-{\operatorname{Re}} z} N^{\sigma} d\sigma \ll N (\log N)^{{\operatorname{Re}} z -3/2+ \varepsilon}. \end{align*} $$
$$ \begin{align*}\ll (\log N)^{1/2 +\varepsilon} \int_{1-(\log N)^{-1/2}}^{1-r} (1-\sigma)^{1-{\operatorname{Re}} z} N^{\sigma} d\sigma \ll N (\log N)^{{\operatorname{Re}} z -3/2+ \varepsilon}. \end{align*} $$
Similarly, the (nearly) circular portion of
![]() $\Gamma _3$
contributes
$\Gamma _3$
contributes
since
![]() $r \leq 1/\log N$
. Thus, the error term in (A.5) is
$r \leq 1/\log N$
. Thus, the error term in (A.5) is
![]() $\ll N (\log N)^{{\operatorname {Re}} z- 3/2+ \varepsilon }$
.
$\ll N (\log N)^{{\operatorname {Re}} z- 3/2+ \varepsilon }$
.
Turning to the main term in (A.5), we claim that
 $$ \begin{align} \frac{1}{2 \pi i }\int_{\Gamma_3} N^s (s - 1)^{-z} ds = \frac{1}{\Gamma(z)} N (\log N)^{z-1} + O(N (\log N)^{-100}). \end{align} $$
$$ \begin{align} \frac{1}{2 \pi i }\int_{\Gamma_3} N^s (s - 1)^{-z} ds = \frac{1}{\Gamma(z)} N (\log N)^{z-1} + O(N (\log N)^{-100}). \end{align} $$
To obtain (A.6), denote by
![]() $\mathcal {H}$
(the Hankel contour) the contour obtained from
$\mathcal {H}$
(the Hankel contour) the contour obtained from
![]() $\Gamma _3$
by extending both horizontal parts out to
$\Gamma _3$
by extending both horizontal parts out to
![]() $-\infty $
. The integral in (A.6) extended over
$-\infty $
. The integral in (A.6) extended over
![]() $\mathcal {H}$
is equal to
$\mathcal {H}$
is equal to
![]() $\frac {1}{\Gamma (z)} N(\log N)^{z-1}$
, as follows from the standard Hankel integral [Reference Tenenbaum17, Theorem II.0.17] and a substitution. Now, note that
$\frac {1}{\Gamma (z)} N(\log N)^{z-1}$
, as follows from the standard Hankel integral [Reference Tenenbaum17, Theorem II.0.17] and a substitution. Now, note that
 $$ \begin{align*} \int_{\mathcal{H}\setminus \Gamma_3} |N^s (s - 1)^{-z}||ds| & \ll \int_{-\infty}^{1-(\log N)^{-1/2}} N^{\sigma} (1-\sigma)^{-{\operatorname{Re}} z} d\sigma \\ & \ll N^{1-(\log N)^{-1/2}} (\log N)^{O(1)}, \end{align*} $$
$$ \begin{align*} \int_{\mathcal{H}\setminus \Gamma_3} |N^s (s - 1)^{-z}||ds| & \ll \int_{-\infty}^{1-(\log N)^{-1/2}} N^{\sigma} (1-\sigma)^{-{\operatorname{Re}} z} d\sigma \\ & \ll N^{1-(\log N)^{-1/2}} (\log N)^{O(1)}, \end{align*} $$
which is much smaller than
![]() $N(\log N)^{-100}$
, and thus establishes the claim (A.6). Putting all this together gives
$N(\log N)^{-100}$
, and thus establishes the claim (A.6). Putting all this together gives
 $$ \begin{align*}I_3= {\mathcal H}(1;z,j) N \frac{(\log N)^{z-1}}{\Gamma(z)} + O \big( N (\log N)^{{\operatorname{Re}} z -3/2 +\varepsilon} \big). \end{align*} $$
$$ \begin{align*}I_3= {\mathcal H}(1;z,j) N \frac{(\log N)^{z-1}}{\Gamma(z)} + O \big( N (\log N)^{{\operatorname{Re}} z -3/2 +\varepsilon} \big). \end{align*} $$
Combining this with our estimates for
![]() $I_1$
,
$I_1$
,
![]() $I_2$
,
$I_2$
,
![]() $I_4$
and
$I_4$
and
![]() $I_5$
, from (A.2) we conclude that
$I_5$
, from (A.2) we conclude that
 $$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} f(n) z^{\Omega(n)}e^{-n/N} = {\mathcal H}(1;z,j) N \frac{(\log N)^{z-1}}{\Gamma(z)} + O_{\varepsilon} \Big( N (\log N)^{{\operatorname{Re}} z -3/2 +\varepsilon} \Big). \end{align} $$
$$ \begin{align} \sum_{n\in {\mathcal A}_j(k)} f(n) z^{\Omega(n)}e^{-n/N} = {\mathcal H}(1;z,j) N \frac{(\log N)^{z-1}}{\Gamma(z)} + O_{\varepsilon} \Big( N (\log N)^{{\operatorname{Re}} z -3/2 +\varepsilon} \Big). \end{align} $$
Finally, in the context of Section 9 note that (using (9.3), and since
![]() $\lim _{s\to 1} (s-1) \zeta (s)= 1$
)
$\lim _{s\to 1} (s-1) \zeta (s)= 1$
)
while in the context of Section 10 (using (10.4))
Acknowledgments
This work began at the 2022 Oberwolfach Analytic Number Theory meeting, and it is a pleasure to thank the Mathematisches Forschungsinstitut Oberwolfach for the stimulating working conditions. BG is supported by a Simons Investigator grant and is grateful to the Simons Foundation for their continued support. KS is supported in part by a Simons Investigator award from the Simons foundation and a grant from the National Science Foundation.
Competing interest
None.