Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-19T07:14:43.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Avoiding families and Tukey functions on the nowhere-dense ideal

Part of: Set theory

Published online by Cambridge University Press:  01 September 2010

Sławomir Solecki  and
Stevo Todorcevic
Sławomir Solecki
Affiliation:
Department of Mathematics, University of Illinois, 1409 W. Green Street, Urbana, IL 61801, USA ([email protected])
Stevo Todorcevic
Affiliation:
Université Paris 7-CNRS, FRE 3233, 2, place Jussieu, 75251 Paris Cedex 05, France ([email protected]) and Department of Mathematics, University of Toronto, 40 St. George Street, Toronto M5S 2E4, Canada
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate Tukey functions from the ideal of all closed nowhere-dense subsets of 2ℕ. In particular, we answer an old question of Isbell and Fremlin by showing that this ideal is not Tukey reducible to the ideal of density zero subsets of ℕ. We also prove non-existence of various special types of Tukey reductions from the nowhere-dense ideal to analytic P-ideals. In connection with these results, we study families 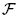of clopen subsets of 2ℕ with the property that for each nowhere-dense subset of 2ℕ there is a set in 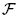not intersecting it. We call such families avoiding.

Keywords

Tukey reductionsnowhere-dense setsanalytic P-ideals

MSC classification

Secondary: 03E05: Other combinatorial set theory 03E15: Descriptive set theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 10 , Issue 2 , April 2011 , pp. 405 - 435
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bartoszyński, T., Additivity of measure implies additivity of category, Trans. Am. Math. Soc. 281 (1984), 209–213.CrossRefGoogle Scholar
2.Farah, I., Ideals induced by Tsirelson submeasures, Fund. Math. 159 (1999), 243–258.CrossRefGoogle Scholar
3.Fremlin, D. H., The partially ordered sets of measure theory and Tukey's ordering, Note Mat. 11 (1991), 177–214.Google Scholar
4.Fremlin, D. H., Families of compact sets and Tukey ordering, Atti Sem. Mat. Fis. Univ. Modena 39 (1991), 29–50.Google Scholar
5.Isbell, J. R., Seven cofinal types, J. Lond. Math. Soc. 4 (1972), 651–654.CrossRefGoogle Scholar
6.Kechris, A. S., Classical descriptive set theory (Springer, 1995).CrossRefGoogle Scholar
7.Louveau, A. and Veličković, B., Analytic ideals and cofinal types, Annals Pure Appl. Logic 99 (1999), 171–195.Google Scholar
8.Mátrai, T., On a σ-ideal of compact sets, Topol. Applic. 157 (2010), 1479–1484.Google Scholar
9.Moore, J. T. and Solecki, S., A G δ ideal of compact sets strictly above the nowhere dense ideal in the Tukey order, Annals Pure Appl. Logic 156 (2008), 270–273.Google Scholar
10.Ochan, J. S., Space of subsets of a topological space, Dokl. Akad. Nauk SSSR 32 (1941), 107–109.Google Scholar
11.Raissonier, J. and Stern, J., The strength of measurability hypotheses, Israel J. Math. 50 (1985), 337–349.Google Scholar
12.Solecki, S., Analytic ideals and their applications, Annals Pure Appl. Logic 99 (1999), 51–72.Google Scholar
13.Solecki, S., G δ ideals of compact sets, J. Eur. Math. Soc., in press.Google Scholar
14.Solecki, S. and Todorcevic, S., Cofinal types of topological directed orders, Annales Inst. Fourier 54 (2004), 1877–1911.CrossRefGoogle Scholar
15.Todorcevic, S., Directed sets and cofinal types, Trans. Am. Math. Soc. 290 (1985), 711–723.Google Scholar
16.Todorcevic, S., Partition problems in topology, Contemporary Mathematics, Volume 84 (American Mathematical Society, Providence, RI, 1989).Google Scholar
17.Todorcevic, S., A classification of transitive relations on ℵ1, Proc. Lond. Math. Soc. 73 (1996), 501–533.CrossRefGoogle Scholar
18.Veličković, B., A note on Tsirelson type ideals, Fund. Math. 159 (1999), 259–268.Google Scholar