Let E be an event whose probability of occurrence depends on some continuous variable x, P(E|x) = qx
For example, E may be death and x age, E may be incidence of lung cancer and x amount of smoking, or E may be reconviction of a parolee with x previous criminal convictions (with suitable definitions of the underlying time interval for the occurrence of E). Given observations on n individuals with characteristic x and the incidence of E, it is desired to estimate the function qx.
The simplest case is when the data are grouped—suppose x occurs in nx cases of which E occurs sx times. Then the elementary crude estimate is
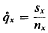
This paper describes a simple, non-parametric method of graduating observed rates or probabilities of the form 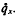 The technique has been used for smoothing data sets arising in medicine and criminology (Copas(1)(2)) and is extended here to an actuarial example and the results compared with more traditional approaches.
The technique has been used for smoothing data sets arising in medicine and criminology (Copas(1)(2)) and is extended here to an actuarial example and the results compared with more traditional approaches.