Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T11:43:34.725Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-parametric graduation using kernel methods

Published online by Cambridge University Press:  20 April 2012

J. B. Copas  and
S. Haberman
J. B. Copas
Affiliation:
University of Birmingham
S. Haberman
Affiliation:
The City University
Get access Rights & Permissions [Opens in a new window]

Extract

Let E be an event whose probability of occurrence depends on some continuous variable x, P(E|x) = qx

For example, E may be death and x age, E may be incidence of lung cancer and x amount of smoking, or E may be reconviction of a parolee with x previous criminal convictions (with suitable definitions of the underlying time interval for the occurrence of E). Given observations on n individuals with characteristic x and the incidence of E, it is desired to estimate the function qx.

The simplest case is when the data are grouped—suppose x occurs in nx cases of which E occurs sx times. Then the elementary crude estimate is

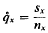
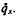This paper describes a simple, non-parametric method of graduating observed rates or probabilities of the form The technique has been used for smoothing data sets arising in medicine and criminology (Copas(1)(2)) and is extended here to an actuarial example and the results compared with more traditional approaches.

Type
Research Article
Information
Journal of the Institute of Actuaries , Volume 110 , Issue 1 , June 1983 , pp. 135 - 156
Copyright
Copyright © Institute and Faculty of Actuaries 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

(1) Copas, J. B. (1982). Plotting p against x. To appear in Applied Statistics.Google Scholar
(2) Copas, J. B. (1982). Regression, prediction and shrinkage. To appear in Journal of Royal Statistical Society, Series B.Google Scholar
(3) Bean, S. J. & Tsokos, C. P. (1980). Developments in non-parametric density estimation. Int. Statist. Rev. 48, 267.CrossRefGoogle Scholar
(4) Rosenblatt, M. (1956). Remarks on some non-parametric estimates of a density function. Ann. Math. Stat. 21, 832.CrossRefGoogle Scholar
(5) Benjamin, B. & Pollard, J. H. (1980). The Analysis of Mortality and Other Actuarial Statistics. Heinemann, London.Google Scholar
(6) Spencer, J. (1904). On the graduation of the rates of sickness and mortality presented by the experience of the Manchester Unity of Oddfellows during the period 1893 – 1897. J.I.A. 38, 334.Google Scholar
(7) Parzen, E. (1962). On the estimation of a probability density function and the mode. Ann. Math. Stat. 40. 1065.CrossRefGoogle Scholar
(8) Collomb, G. (1981). Estimation non-paramétrique de la régression: Revue bibliographique. Int. Statist. Rev. 49, 75.CrossRefGoogle Scholar
(9) Registrar General (1968). Decennial Supplement. English Life Tables No. 12. H.M.S.O., London.Google Scholar
(10) Lidstone, G. J. (1892). On an application of the graphic method to obtain a graduated mortality table. J.I.A. 30, 212.Google Scholar
(11) McCutcheon, J. J. & Eilbeck, J. C. (1977). Experiments in the graduation of the English Life Tables (No. 13) data. T.F.A. 35, 281.Google Scholar