Gabardo and Nashed [‘Nonuniform multiresolution analyses and spectral pairs’, J. Funct. Anal. 158(1) (1998), 209–241] have introduced the concept of nonuniform multiresolution analysis (NUMRA), based on the theory of spectral pairs, in which the associated translated set
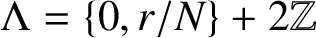 $\Lambda =\{0,{r}/{N}\}+2\mathbb Z$
is not necessarily a discrete subgroup of
$\Lambda =\{0,{r}/{N}\}+2\mathbb Z$
is not necessarily a discrete subgroup of
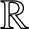 $\mathbb{R}$
, and the translation factor is
$\mathbb{R}$
, and the translation factor is
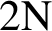 $2\textrm{N}$
. Here r is an odd integer with
$2\textrm{N}$
. Here r is an odd integer with
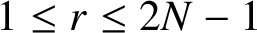 $1\leq r\leq 2N-1$
such that r and N are relatively prime. The nonuniform wavelets associated with NUMRA can be used in signal processing, sampling theory, speech recognition and various other areas, where instead of integer shifts nonuniform shifts are needed. In order to further generalize this useful NUMRA, we consider the set
$1\leq r\leq 2N-1$
such that r and N are relatively prime. The nonuniform wavelets associated with NUMRA can be used in signal processing, sampling theory, speech recognition and various other areas, where instead of integer shifts nonuniform shifts are needed. In order to further generalize this useful NUMRA, we consider the set
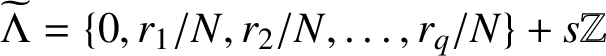 $\widetilde {\Lambda }=\{0,{r_1}/{N},{r_2}/{N},\ldots ,{r_q}/{N}\}+s\mathbb Z$
, where s is an even integer,
$\widetilde {\Lambda }=\{0,{r_1}/{N},{r_2}/{N},\ldots ,{r_q}/{N}\}+s\mathbb Z$
, where s is an even integer,
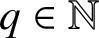 $q\in \mathbb {N}$
,
$q\in \mathbb {N}$
,
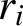 $r_i$
is an integer such that
$r_i$
is an integer such that
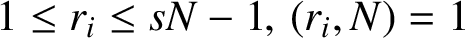 $1\leq r_i\leq sN-1,\,(r_i,N)=1$
for all i and
$1\leq r_i\leq sN-1,\,(r_i,N)=1$
for all i and
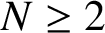 $N\geq 2$
. In this paper, we prove that the concept of NUMRA with the translation set
$N\geq 2$
. In this paper, we prove that the concept of NUMRA with the translation set
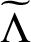 $\widetilde {\Lambda }$
is possible only if
$\widetilde {\Lambda }$
is possible only if
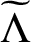 $\widetilde {\Lambda }$
is of the form
$\widetilde {\Lambda }$
is of the form
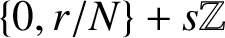 $\{0,{r}/{N}\}+s\mathbb Z$
. Next we introduce
$\{0,{r}/{N}\}+s\mathbb Z$
. Next we introduce
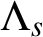 $\Lambda _s$
-nonuniform multiresolution analysis (
$\Lambda _s$
-nonuniform multiresolution analysis (
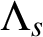 $\Lambda _s$
-NUMRA) for which the translation set is
$\Lambda _s$
-NUMRA) for which the translation set is
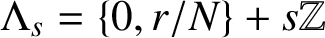 $\Lambda _s=\{0,{r}/{N}\}+s\mathbb Z$
and the dilation factor is
$\Lambda _s=\{0,{r}/{N}\}+s\mathbb Z$
and the dilation factor is
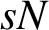 $sN$
, where s is an even integer. Also, we characterize the scaling functions associated with
$sN$
, where s is an even integer. Also, we characterize the scaling functions associated with
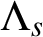 $\Lambda _s$
-NUMRA and we give necessary and sufficient conditions for wavelet filters associated with
$\Lambda _s$
-NUMRA and we give necessary and sufficient conditions for wavelet filters associated with
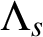 $\Lambda _s$
-NUMRA.
$\Lambda _s$
-NUMRA.
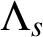 $\Lambda _s$
-NONUNIFORM MULTIRESOLUTION ANALYSIS
$\Lambda _s$
-NONUNIFORM MULTIRESOLUTION ANALYSIS