Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T13:28:22.217Z Has data issue: false hasContentIssue false
  • English
  • Français

Varieties of completely regular semigroups

Part of: Semigroups

Published online by Cambridge University Press:  09 April 2009

Norman R. Reilly
Norman R. Reilly
Affiliation:
Deparment of Mathematics and Statistics, Simon Fraser UniversityBurnaby, B. C. V5A 1A6, Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

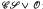If CS(respectively, O) denotes the class of all completely simple semigroups (respectively, semigroups that are orthodox unions of groups) then CS(respectively, O) is a variety of algebras with respect to the operations of multiplication and inversion. The main result shows that the lattice of subvarieties of is a precisely determined subdirect product of the lattice of subvarieties of CSand the lattice of subvarieties of O. A basis of identities is obtained for any variety 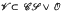in terms of bases of identities for 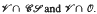. Several operators on the lattice of subvarieties of 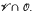are also introduced and studied.

MSC classification

Secondary: 20M07: Varieties and pseudovarieties of semigroups 20M10: General structure theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 38 , Issue 3 , June 1985 , pp. 372 - 393
Copyright
Copyright © Australian Mathematical Society 1985

References

[1]Birjukov, A. P., ‘Varieties of idempotent semigroups’, Algebra i Logika 9 (1970), 255–273 (Russian)Google Scholar
[2]Fennemore, C. F., ‘All varieties of bands’, Math. Nachr. 4 (1971); I: 237–255; II: 253–262.Google Scholar
[3]Gerhard, J. A., ‘The lattice of equational classes of idempotent semigroups’, J. Algebra 15 (1970), 195–224.CrossRefGoogle Scholar
[4]Gerhard, J. A., and Petrich, M., ‘All varieties of regular orthogroups’, manuscript.Google Scholar
[5]Hall, T. E., ‘On regular semigroups’, J. Algebra 24 (1973), 1–24.CrossRefGoogle Scholar
[6]Hall, T. E., and Jones, P. R., ‘On the lattice of varieties of bands of groups’, Pacific J. Math. 91 (1980) 327–337.CrossRefGoogle Scholar
[7]Howie, J. M., An introduction to semigroup theory (Academic Press, London, 1976).Google Scholar
[8]Jones, P. R., ‘Completely simple semigroups: free products, free semigroups and varieties’, Proc. Roy. Soc. Edinburgh Sect. A 88 (1981), 293–313.CrossRefGoogle Scholar
[9]Jones, P. R., ‘Varieties of completely regular semigroups’, J. Austral. Math. Soc. (Series A) 35 (1983), 227–235.CrossRefGoogle Scholar
[10]Petrich, M., ‘Varieties of orthodox bands of groups’, Pacific J. Math. 58 (1975), 209–217.CrossRefGoogle Scholar
[11]Petrich, M., ‘Certain varieties and quasivarieties of completely regular semigroups’, Canad. J. Math. 29, (1977), 1171–1197.CrossRefGoogle Scholar
[12]Petrich, M., ‘On the varieties of completely regular semigroups’, Semigroup Forum 25 (1982) 153–169.CrossRefGoogle Scholar
[13]Petrich, M., and Reilly, N. R., ‘A network of congruences on an inverse sernigroup’, Trans. Amer. Math. Soc. 270 (1982), 309–325.CrossRefGoogle Scholar
[14]Petrich, M. and Reilly, N. R., ‘Bands of groups with universal properties’, Monatshefte für Mathematik 94 (1982), 45–67.CrossRefGoogle Scholar
[15]Petrich, M. and Reilly, N. R., ‘Varieties of groups and of completely simple semigroups’, Bull. Austral. Math. Soc. 23 (1981), 339–359.CrossRefGoogle Scholar
[16]Petrich, M. and Reilly, N. R., ‘Near varieties of idempotent generated completely simple semigroups’, Algebra Universalis 16 (1983), 83–104.CrossRefGoogle Scholar
[17]Petrich, M. and Reilly, N. R., ‘All varieties of central completely simple semigroups’, Trans. Amer. Math. Soc. 280 (1983), 623–636.CrossRefGoogle Scholar
[18]Petrich, M. and Reilly, N. R., ‘Certain homomorphism of the lattice of varieties of completely simple semigroups’, J. Austral. Math. Soc. (to appear).Google Scholar
[19]Rasin, V. V., ‘On the lattice of varieties of completely simple semigroups’, Semi group Forum 17 (1979), 113–122.CrossRefGoogle Scholar
[20]Rasin, V. V., ‘On the varieties of Cliffordian semigroups’, Semigroup Forum 23 (1981), 201–220.CrossRefGoogle Scholar
[21]Wismath, S., ‘The lattice of varieties and pseudovarieties of band monoids’, Thesis, Simon Fraser University, 1983.Google Scholar
[22]Wismath, S., ‘The lattice of varieties and pseudovarieties of band monoids’. manuscript.Google Scholar