Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T14:23:52.319Z Has data issue: false hasContentIssue false
  • English
  • Français

A VARIATIONAL PROBLEM FOR CURVES ON FINSLER SURFACES

Part of: Existence theories Infinite-dimensional manifolds

Published online by Cambridge University Press:  13 May 2016

SORIN V. SABAU  and
KAZUHIRO SHIBUYA
SORIN V. SABAU*
Affiliation:
Department of Mathematics, Tokai University, Sapporo, 005-8601, Japan email [email protected]
KAZUHIRO SHIBUYA
Affiliation:
Graduate School of Science, Hiroshima University, Hiroshima, 739-8521, Japan email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the variational problem for 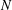$N$-parallel curves on a Finsler surface by means of exterior differential systems using Griffiths’ method. We obtain the conditions when these curves are extremals of a length functional and write the explicit form of Euler–Lagrange equations for this type of variational problem.

Keywords

exterior differential systemsvariational problemsFinsler surfaces

MSC classification

Primary: 49J40: Variational methods including variational inequalities
Secondary: 58B20: Riemannian, Finsler and other geometric structures
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 101 , Issue 3 , December 2016 , pp. 418 - 430
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Abraham, R. and Marsden, J., Foundations of Mechanics: Second Edition (American Mathematical Society, Chelsea, Providence, RI, 2008).Google Scholar
Bao, D., ‘On two curvature-driven problems in Riemann–Finsler geometry’, Adv. Stud. Pure Math. 48 (2007), 19–71; Finsler Geometry, Sapporo 2005.Google Scholar
Bao, D., Chern, S. S. and Shen, Z., An Introduction to Riemann Finsler Geometry, Graduate Text in Mathematics, 200 (Springer, New York, 2000).Google Scholar
Bryant, R., ‘On the notions of equivalence of variational problems with one independent variable’, Contemp. Math. 68 (1987), 65–76.Google Scholar
Bryant, R., ‘Projectively flat Finsler 2-spheres of constant curvature’, Selecta Math. (N.S.) 3(2) (1997), 161–203.Google Scholar
Bryant, R., Chern, S. S., Gardner, R., Goldschmidt, H. and Griffiths, P., Exterior Differential Systems, MSRI Publications, 18 (Springer, New York, 1991).Google Scholar
Bryant, R. and Griffiths, Ph., ‘Reduction for constrained variational problems and ∫k 2/2 ds ’, Amer. J. Math. 108 (1986), 525–570.Google Scholar
Griffiths, Ph., Exterior Differential Systems and the Calculus of Variations (Birkhäuser, Basel, 1983).Google Scholar
Hsu, L., ‘Calculus of variations via the Griffiths formalism’, J. Differential Geom. 36 (1992), 551–589.Google Scholar
Itoh, J., Sabau, S. V. and Shimada, H., ‘A Gauss–Bonnet type formula on Riemann–Finsler surfaces with non-constant indicatrix volume’, Kyoto J. Math. 50(1) (2010), 1–224.Google Scholar
Ivey, Th. A. and Landsberg, J. M., Cartan for Beginners; Differential Geometry via Moving Frames and Exterior Differential Systems, Graduate Studies in Mathematics, 61 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Miron, R., Hrimiuc, D., Shimada, H. and Sabau, S. V., The Geometry of Hamilton and Lagrange Spaces, Fundamental Theories of Physics, 118 (Kluwer Academic, 2001).Google Scholar
Olver, P., Equivalence, Invariants, and Symmetry (Cambridge University Press, New York, 1995).Google Scholar
Sabau, S. V. and Shimada, H., ‘Riemann–Finsler surfaces’, Adv. Stud. Pure Math. 48 (2007), 125–162; Finsler Geometry, Sapporo 2005.Google Scholar
Shen, Z., Lectures on Finsler Geometry (World Scientific, Singapore, 2001).Google Scholar
Szabó, Z., ‘Positive definite Berwald spaces (structure theorems on Berwald spaces)’, Tensor (N.S.) 35 (1981), 25–39.Google Scholar