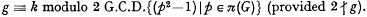Let G be a finite group of order g having exactly k conjugate classes. Let π(G) denote the set of prime divisors of g. K. A. Hirsch [4] has shown that By the same methods we prove g ≡ k modulo G.C.D. {(p–1)2 p ∈ π(G)} and that if G is a p-group, g = h modulo (p−1)(p2−1). It follows that k has the form (n+r(p−1)) (p2−1)+pe where r and n are integers ≧ 0, p is a prime, e is 0 or 1, and g = p2n+e. This has been established using representation theory by Philip Hall [3] (see also [5]). If 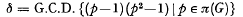then simple examples show (for 6 ∤ g obviously) that g ≡ k modulo σ or even σ/2 is not generally true.