Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T10:42:37.682Z Has data issue: false hasContentIssue false
  • English
  • Français

The transient behaviour of the queueing system Gi/M/1

Published online by Cambridge University Press:  09 April 2009

P. J. Brockwell
P. J. Brockwell
Affiliation:
University of Melbourne.
Rights & Permissions [Opens in a new window]

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a single server queue for which the interarrival times are identically and independently distributed with distribution function A(x) and whose service times are distributed independently of each other and of the interarrival times with distribution function B(x) = 1 − e−x, x ≧ 0. We suppose that the system starts from emptiness and use the results of P. D. Finch [2] to derive an explicit expression for qnj, the probability that the (n + 1)th arrival finds more than j customers in the system. The special cases M/M/1 and D/M/1 are considerend and it is shown in the general case that qnj is a partial sum of the usual Lagrange series for the limiting probability .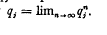

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 3 , Issue 2 , May 1963 , pp. 249 - 256
Copyright
Copyright © Australian Mathematical Society 1963

References

[1]Conolly, B. W., The busy period in relation to the queueing system GI/M/1, Biometrika 46, 246–251 (1959).Google Scholar
[2]Finch, P. D., The single server queueing system with non-recurrent input process and Erlang service time, to appear in this Journal.Google Scholar
[3]Finch, P. D., On the transient behaviour of a simple queue, J.R.S.S. (B) 22 277–284 (1960).Google Scholar
[4]Finch, P. D., On the busy period in the queueing system GI/G/1, this Journal 2 217–228 (1961).Google Scholar
[5]Prabhu, N. U., Some results for the quene with Poisson arrivals, J.R.S.S. (B) 22 104–107 (1960).Google Scholar
[6]Takács, L., Transient behaviour of single server queueing processes with recurrent input and exponentially distributed service times, Opns. Res. 8 231–245 (1960).CrossRefGoogle Scholar
[7]Pollaczek, F., Problèmes stochastiques poses par le phénomène de formation d'une queue d'attente à un guichet et par des phénomènes apparentes, Mémorial des Sciences Mathématiques (Gauthier-Villars, Paris, 1957).Google Scholar