Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T19:57:57.420Z Has data issue: false hasContentIssue false
  • English
  • Français

SYMMETRIC CROSSCAP NUMBER OF GROUPS OF ORDER LESS THAN OR EQUAL TO 63

Part of: Special aspects of infinite or finite groups Low-dimensional topology Other groups of matrices Riemann surfaces

Published online by Cambridge University Press:  23 December 2016

ADRIÁN BACELO Open the ORCID record for ADRIÁN BACELO [Opens in a new window]
ADRIÁN BACELO*
Affiliation:
Departamento de Álgebra, Facultad de Matemáticas, Universidad Complutense, 28040 Madrid, Spain email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Every finite group 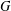$G$ acts on some nonorientable unbordered surfaces. The minimal topological genus of those surfaces is called the symmetric crosscap number of 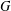$G$. It is known that 3 is not the symmetric crosscap number of any group but it remains unknown whether there are other such values, called gaps. In this paper we obtain group presentations which allow one to find the actions realizing the symmetric crosscap number of groups of each group of order less than or equal to 63.

Keywords

Riemann surfacesGroup theoryKlein surfaces

MSC classification

Primary: 57M60: Group actions in low dimensions
Secondary: 20F05: Generators, relations, and presentations 20H10: Fuchsian groups and their generalizations 30F50: Klein surfaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 2 , October 2017 , pp. 145 - 156
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Alling, N. L. and Greenleaf, N., Foundations of the Theory of Klein Surfaces, Lecture Notes in Mathematics, 219 (Springer, Berlin–New York, 1971).CrossRefGoogle Scholar
Bacelo, A., ‘Los grupos de género imaginario menor que 10’, Trabajo Fin de Master, Universidad Complutense, Madrid, 2013.Google Scholar
Bacelo, A., ‘Sobre el género imaginario de grupos finitos’, Tesis Doctoral, Universidad Complutense, Madrid, 2015.Google Scholar
Bacelo, A., Etayo, J. J. and Martínez, E., ‘Filling gaps of the symmetric crosscap spectrum’, Preprint, 2015.Google Scholar
Bujalance, E., ‘Cyclic groups of automorphisms of compact non-orientable Klein surfaces without boundary’, Pacific J. Math. 109 (1983), 279–289.Google Scholar
Bujalance, E., Etayo, J. J. and Martínez, E., ‘The full group of automorphisms of non-orientable unbordered Klein surfaces of topological genus 3, 4 and 5’, Rev. Mat. Complut. 27 (2014), 305–326.Google Scholar
Conder, M., http://www.math.auckland.ac.nz/∼conder/.Google Scholar
Etayo, J. J., ‘Sobre grupos de automorfismos de superficies de Klein’, Tesis Doctoral, Universidad Complutense, Madrid, 1983.Google Scholar
Etayo, J. J. and Martínez, E., ‘The symmetric crosscap number of the groups C m × D n ’, Proc. Roy. Soc. Edinburgh Sect. A 138 (2008), 1197–1213.Google Scholar
Etayo, J. J. and Martínez, E., ‘The action of the groups D m × D n on unbordered Klein surfaces’, Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 102 (2011), 97–108.Google Scholar
Etayo, J. J. and Martínez, E., ‘The symmetric crosscap number of the groups DC 3 × C n and A 4 × C n ’, Houston J. Math. 38 (2012), 345–358.Google Scholar
Etayo, J. J. and Martínez, E., ‘The symmetric crosscap number of the groups of small-order’, J. Algebra Appl. 12 1250164 (2013), 16 pp.Google Scholar
Etayo, J. J. and Martínez, E., ‘The real genus of the groups of order 48’, Collect. Math. 65 (2014), 29–46.Google Scholar
Gromadzki, G., ‘Abelian groups of automorphisms of compact non-orientable Klein surfaces without boundary’, Comment. Math. Prace Mat. 28 (1989), 197–217.Google Scholar
Hall, M. Jr. and Senior, J. K., The Groups of Order 2 n (n ≤ 6) (McMillan, New York, 1964).Google Scholar
Macbeath, A. M., ‘The classification of non-Euclidean crystallographic groups’, Canad. J. Math. 19 (1967), 1192–1205.Google Scholar
May, C. L., ‘The symmetric crosscap number of a group’, Glasg. Math. J. 41 (2001), 399–410.Google Scholar
Preston, R., ‘Projective structures and fundamental domains on compact Klein surfaces’, Thesis, University of Texas, 1975.Google Scholar
Singerman, D., ‘Automorphisms of compact non-orientable Riemann surfaces’, Glasg. Math. J. 12 (1971), 50–59.CrossRefGoogle Scholar
Tomé, R., ‘Aplicación de la teoría de grupos al cubo de Rubik desde un punto de vista superior’, Trabajo Fin de Grado, Universidad Complutense, Madrid, 2015.Google Scholar
Tucker, T. W., ‘Symmetric embeddings of Cayley graphs in non-orientable surfaces’, in: Graph Theory, Combinatorics and Applications (eds. Alavy, I. et al. ) (Wiley, New York, 1991), 1105–1120.Google Scholar
Wilkie, H. C., ‘On non-Euclidean crystallographic groups’, Math. Z. 91 (1966), 87–102.CrossRefGoogle Scholar