Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-23T03:05:34.486Z Has data issue: false hasContentIssue false
  • English
  • Français

Stone algebras form an equational class: (Remarks on Lattice Theory III)

Published online by Cambridge University Press:  09 April 2009

G. Grätzer
G. Grätzer
Affiliation:
University of Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

To prove the statement given in the title take a set Σ1 of identities characterizing distributive lattices 〈L; ∨, ∧, 0, 1〉 with 0 and 1, and let Then is Σ redundant set of identities characterizing Stone algebras 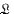= 〈L; ∨, ∧, *, 0, 1〉. To show that we only have to verify that for a ∈ L, a* is the pseudo-complement of a. Indeed, a ∧ a* 0; now, if a ∧ x = 0, then a* ∨ x* 0* = 1, and a** ∧ = 1* = 0; since a** is the complement of a*, the last identity implies x** ≦ a*, thus x ≦ x** ≦ a*, which was to be proved.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 9 , Issue 3-4 , May 1969 , pp. 308 - 309
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Birkhoff, G., ‘Lattice theory’, Amer. Math. Soc. Colloq. Publ. 25, (1940, 1948, 1967).Google Scholar
[2]Grätzer, G., ‘A generalization of Stone's representation theorem for Boolean algebras’, Duke Math. J. 30 (1963), 469–474.CrossRefGoogle Scholar
[3]Speed, T. P., ‘On Stone lattices’, Journ. Aust. Math. Soc. 9 (1969), 297–307.CrossRefGoogle Scholar