No CrossRef data available.
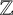 $\mathbb {Z}$-COVERS OF A FINITE GRAPH AND MAHLER MEASURES
$\mathbb {Z}$-COVERS OF A FINITE GRAPH AND MAHLER MEASURESPublished online by Cambridge University Press: 28 October 2024
Using the special value at 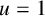 $u=1$ of Artin–Ihara L-functions, we associate to every
$u=1$ of Artin–Ihara L-functions, we associate to every 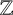 $\mathbb {Z}$-cover of a finite connected graph a polynomial, which we call the Ihara polynomial. We show that the number of spanning trees for the finite intermediate graphs of such a cover can be expressed in terms of the Pierce–Lehmer sequence associated to a factor of the Ihara polynomial. This allows us to express the asymptotic growth of the number of spanning trees in terms of the Mahler measure of this polynomial. Specialising to the situation where the base graph is a bouquet or the dumbbell graph gives us back previous results in the literature for circulant and I-graphs (including the generalised Petersen graphs). We also express the p-adic valuation of the number of spanning trees of the finite intermediate graphs in terms of the p-adic Mahler measure of the Ihara polynomial. When applied to a particular
$\mathbb {Z}$-cover of a finite connected graph a polynomial, which we call the Ihara polynomial. We show that the number of spanning trees for the finite intermediate graphs of such a cover can be expressed in terms of the Pierce–Lehmer sequence associated to a factor of the Ihara polynomial. This allows us to express the asymptotic growth of the number of spanning trees in terms of the Mahler measure of this polynomial. Specialising to the situation where the base graph is a bouquet or the dumbbell graph gives us back previous results in the literature for circulant and I-graphs (including the generalised Petersen graphs). We also express the p-adic valuation of the number of spanning trees of the finite intermediate graphs in terms of the p-adic Mahler measure of the Ihara polynomial. When applied to a particular 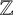 $\mathbb {Z}$-cover, our result gives us back Lengyel’s calculation of the p-adic valuations of Fibonacci numbers.
$\mathbb {Z}$-cover, our result gives us back Lengyel’s calculation of the p-adic valuations of Fibonacci numbers.
The first author received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement number 945714). Moreover, the first author thanks the research projects ‘Motivic homotopy, quadratic invariants and diagonal classes’ (ANR-21-CE40-0015) and IRN GANDA for their financial support. Both authors are grateful to the Max Planck Institute for Mathematics in Bonn for providing excellent working conditions, great hospitality and financial support.
Communicated by Michael Giudici