Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T14:22:26.041Z Has data issue: false hasContentIssue false
  • English
  • Français

SEMISIMPLICITY OF HECKE AND (WALLED) BRAUER ALGEBRAS

Part of: Lie algebras and Lie superalgebras Representation theory of groups

Published online by Cambridge University Press:  25 October 2016

HENNING HAAHR ANDERSEN ,
CATHARINA STROPPEL  and
DANIEL TUBBENHAUER
HENNING HAAHR ANDERSEN
Affiliation:
Aarhus University, Centre for Quantum Geometry of Moduli Spaces, Ny Munkegade 118, Building 1530, Room 327, 8000 Aarhus C, Denmark email [email protected]
CATHARINA STROPPEL
Affiliation:
Universität Bonn, Mathematisches Institut, Endenicher Allee 60, Room 4.007, 53115 Bonn, Germany email [email protected]
DANIEL TUBBENHAUER*
Affiliation:
Universität Bonn, Mathematisches Institut, Endenicher Allee 60, Room 1.003, 53115 Bonn, Germany email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show how to use Jantzen’s sum formula for Weyl modules to prove semisimplicity criteria for endomorphism algebras of $\mathbf{U}_{q}$-tilting modules (for any field 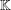$\mathbb{K}$ and any parameter $q\in \mathbb{K}-\{0,-1\}$). As an application, we recover the semisimplicity criteria for the Hecke algebras of types 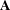$\mathbf{A}$ and 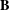$\mathbf{B}$, the walled Brauer algebras and the Brauer algebras from our more general approach.

Keywords

quantum groups(quantum) tilting modulesJantzen’s sum formulassemisimplicityHecke and Brauer algebras

MSC classification

Primary: 17B37: Quantum groups (quantized enveloping algebras) and related deformations
Secondary: 17B10: Representations, algebraic theory (weights) 20C08: Hecke algebras and their representations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 1 , August 2017 , pp. 1 - 44
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

Elements of the text in the article appear in colour online available at 10.1017/S1446788716000392.

H.H.A. was supported by the Center of Excellence grant ‘Centre for Quantum Geometry of Moduli Spaces (QGM)’ from the Danish National Research Foundation (DNRF), C.S. by a Hirzebruch professorship of the Max-Planck-Gesellschaft and D.T. by a research funding of the Deutsche Forschungsgemeinschaft (DFG) during this work.

References

Andersen, H. H., Tilting Modules for Algebraic and Quantum Groups, NATO Science Series II: Mathematics, Physics and Chemistry, 28 (Kluwer Academic, Dordrecht, 2001).CrossRefGoogle Scholar
Andersen, H. H. and Kulkarni, U., ‘Sum formulas for reductive algebraic groups’, Adv. Math. 217(1) (2008), 419–447.CrossRefGoogle Scholar
Andersen, H. H., Polo, P. and Wen, K. X., ‘Representations of quantum algebras’, Invent. Math. 104(1) (1991), 1–59.Google Scholar
Andersen, H. H., Stroppel, C. and Tubbenhauer, D., ‘Additional notes for the paper “Cellular structures using $\mathbf{U}_{q}$ -tilting modules”’, eprint, http://pure.au.dk/portal/files/100562565/cell_tilt_proofs_1.pdf, http://www.math.uni-bonn.de/ag/stroppel/cell-tilt-proofs_neu.pdf, http://www.math.uni-bonn.de/people/dtubben/cell-tilt-proofs.pdf.Google Scholar
Andersen, H. H., Stroppel, C. and Tubbenhauer, D., ‘Cellular structures using $\mathbf{U}_{q}$ -tilting modules’, arXiv:1503.00224.Google Scholar
Andersen, H. H. and Tubbenhauer, D., ‘Diagram categories for $\mathbf{U}_{q}$ -tilting modules at roots of unity’, Transform. Groups, to appear. Published online (25 January 2016).Google Scholar
Ariki, S., ‘On the semi-simplicity of the Hecke algebra of (ℤ/rℤ) ≀ S n ’, J. Algebra 169(1) (1994), 216–225.Google Scholar
Brauer, R., ‘On algebras which are connected with the semisimple continuous groups’, Ann. of Math. (2) 38(4) (1937), 857–872.CrossRefGoogle Scholar
Brown, W. P., ‘The semisimplicity of 𝜔 f n ’, Ann. of Math. (2) 63 (1956), 324–335.CrossRefGoogle Scholar
Brundan, J. and Stroppel, C., ‘Gradings on walled Brauer algebras and Khovanov’s arc algebra’, Adv. Math. 231(2) (2012), 709–773.CrossRefGoogle Scholar
Cox, A., De Visscher, M., Doty, S. and Martin, P., ‘On the blocks of the walled Brauer algebra’, J. Algebra 320(1) (2008), 169–212.Google Scholar
Dipper, R., Doty, S. and Stoll, F., ‘The quantized walled Brauer algebra and mixed tensor space’, Algebr. Represent. Theory 17(2) (2014), 675–701.CrossRefGoogle Scholar
Dipper, R. and James, G., ‘Representations of Hecke algebras of type B n ’, J. Algebra 146(2) (1992), 454–481.CrossRefGoogle Scholar
Donkin, S., The q-Schur Algebra, London Mathematical Society Lecture Note Series, 253 (Cambridge University Press, Cambridge, 1998).Google Scholar
Donkin, S. and Tange, R., ‘The Brauer algebra and the symplectic Schur algebra’, Math. Z. 265(1) (2010), 187–219.Google Scholar
Doran, W. F. IV, Wales, D. B. and Hanlon, P. J., ‘On the semisimplicity of the Brauer centralizer algebras’, J. Algebra 211 (1999), 647–685.Google Scholar
Du, J., Parshall, B. and Scott, L., ‘Quantum Weyl reciprocity and tilting modules’, Comm. Math. Phys. 195(2) (1998), 321–352.Google Scholar
Ehrig, M. and Stroppel, C., ‘Schur–Weyl duality for the Brauer algebra and the ortho-symplectic Lie superalgebra’, Math. Z. 284(1–2) (2016), 595–613.Google Scholar
Goodman, R. and Wallach, N. R., Symmetry, Representations, and Invariants, Graduate Texts in Mathematics, 255 (Springer, Dordrecht, 2009).Google Scholar
Graham, J. J. and Lehrer, G., ‘Cellular algebras’, Invent. Math. 123(1) (1996), 1–34.Google Scholar
Gyoja, A. and Uno, K., ‘On the semisimplicity of Hecke algebras’, J. Math. Soc. Japan 41(1) (1989), 75–79.Google Scholar
Härterich, M., ‘Murphy bases of generalized Temperley–Lieb algebras’, Arch. Math. (Basel) 72(5) (1999), 337–345.CrossRefGoogle Scholar
Hu, J., ‘Schur–Weyl reciprocity between quantum groups and Hecke algebras of type G (r, 1, n)’, Math. Z. 238(3) (2001), 505–521.Google Scholar
Hu, J., ‘BMW algebra, quantized coordinate algebra and type C Schur–Weyl duality’, Represent. Theory 15 (2011), 1–62.Google Scholar
Hu, J. and Stoll, F., ‘On double centralizer properties between quantum groups and Ariki–Koike algebras’, J. Algebra 275(1) (2004), 397–418.Google Scholar
Humphreys, J. E., Representations of Semisimple Lie Algebras in the BGG Category 𝓞, Graduate Studies in Mathematics, 94 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Jantzen, J. C., ‘Darstellungen halbeinfacher algebraischer Gruppen und zugeordnete kontravariante Formen’, Bonn. Math. Schr. 67 (1973), 124 pages.Google Scholar
Jantzen, J. C., ‘Darstellungen halbeinfacher Gruppen und kontravariante Formen’, J. reine angew. Math. 290 (1977), 117–141.Google Scholar
Jantzen, J. C., Lectures on Quantum Groups, Graduate Studies in Mathematics, 6 (American Mathematical Society, Providence, RI, 1996).Google Scholar
Jantzen, J. C., Representations of Algebraic Groups, 2nd edn, Mathematical Surveys and Monographs, 107 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Kassel, C. and Turaev, V., Braid Groups, Graduate Texts in Mathematics, 247 (Springer, New York, 2008), with the graphical assistance of Olivier Dodane.Google Scholar
Koike, K., ‘On the decomposition of tensor products of the representations of the classical groups: by means of the universal characters’, Adv. Math. 74(1) (1989), 57–86.Google Scholar
Kuperberg, G., ‘Spiders for rank 2 Lie algebras’, Comm. Math. Phys. 180(1) (1996), 109–151.Google Scholar
Lehrer, G. and Zhang, R., ‘Strongly multiplicity free modules for Lie algebras and quantum groups’, J. Algebra 306(1) (2006), 138–174.CrossRefGoogle Scholar
Lehrer, G. and Zhang, R., ‘The second fundamental theorem of invariant theory for the orthogonal group’, Ann. of Math. (2) 176(3) (2012), 2031–2054.Google Scholar
Lusztig, G., Introduction to Quantum Groups, Modern Birkhäuser Classics (Birkhäuser/Springer, New York, 2010), reprint of the 1994 edition.Google Scholar
Lyle, S. and Mathas, A., ‘Blocks of cyclotomic Hecke algebras’, Adv. Math. 216(2) (2007), 854–878.Google Scholar
Martin, P., ‘The structure of the partition algebras’, J. Algebra 183(2) (1996), 319–358.Google Scholar
Mathas, A., Iwahori–Hecke Algebras and Schur Algebras of the Symmetric Group, University Lecture Series, 15 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Mazorchuk, V. and Stroppel, C., ‘ G (ℓ, k, d)-modules via groupoids’, J. Algebraic Combin. 43(1) (2016), 11–32.CrossRefGoogle Scholar
Morton, H. R., ‘A basis for the Birman–Wenzl algebra’, arXiv:1012.3116 (based on joint work with A. J. Wassermann).Google Scholar
Năstăsescu, C., Raianu, Ş. and Van Oystaeyen, F., ‘Modules graded by G-sets’, Math. Z. 203(4) (1990), 605–627.Google Scholar
Paradowski, J., Filtrations of Modules Over the Quantum Algebra, Proceedings of Symposia in Pure Mathematics, 56 (American Mathematical Society, Providence, RI, 1994).Google Scholar
Ram, A. and Ramagge, J., ‘Affine Hecke algebras, cyclotomic Hecke algebras and Clifford theory’, in: A Tribute to C. S. Seshadri, Trends in Mathematics (Birkhäuser, Basel, 2003), 428–466.Google Scholar
Rui, H., ‘A criterion on the semisimple Brauer algebras’, J. Combin. Theory Ser. A 111(1) (2005), 78–88.Google Scholar
Rui, H. and Si, M., ‘A criterion on the semisimple Brauer algebras. II’, J. Combin. Theory Ser. A 113(6) (2006), 1199–1203.Google Scholar
Rui, H. and Si, M., ‘Gram determinants and semisimplicity criteria for Birman–Wenzl algebras’, J. reine angew. Math. 631 (2009), 153–179.Google Scholar
Ryom-Hansen, S., ‘A q-analogue of Kempf’s vanishing theorem’, Mosc. Math. J. 3(1) (2003), 173–187; 260.CrossRefGoogle Scholar
Sakamoto, M. and Shoji, T., ‘Schur–Weyl reciprocity for Ariki–Koike algebras’, J. Algebra 221(1) (1999), 293–314.Google Scholar
Sawin, S. F., ‘Quantum groups at roots of unity and modularity’, J. Knot Theory Ramifications 15(10) (2006), 1245–1277.Google Scholar
Schoutens, H., The Use of Ultraproducts in Commutative Algebra, Lecture Notes in Mathematics, 1999 (Springer, Berlin, 2010).Google Scholar
Thams, L., ‘Two classical results in the quantum mixed case’, J. reine angew. Math. 436 (1993), 129–153.Google Scholar
Turaev, V. G., ‘Operator invariants of tangles, and R-matrices’, Izv. Akad. Nauk SSSR Ser. Mat. 53(5) (1989), 1073–1107; 1135. Translation in Math. USSR-Izv. 35(2) (1990), 411–444.Google Scholar
Wenzl, H., ‘On the structure of Brauer’s centralizer algebras’, Ann. of Math. (2) 128(1) (1988), 173–193.Google Scholar