Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T23:31:09.429Z Has data issue: false hasContentIssue false
  • English
  • Français

Rudin synthesis on homogeneous Banach algebras

Part of: Abstract harmonic analysis Commutative Banach algebras and commutative topological algebras

Published online by Cambridge University Press:  09 April 2009

Rong-Song Jih  and
Hwai-Chiuan Wang
Rong-Song Jih
Affiliation:
National Tsing Hua University TaiwanRepublic of, China
Hwai-Chiuan Wang
Affiliation:
Princeton University, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main results of this article are (I) Let B be a homogeneous Banach algebra, A a closed subalgebra of B, and I the largest closed ideal of B contained in A. We assert that 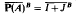for some closed subalgebra J of B. Furthermore, under suitable conditions, we show that A is an R-subalgebra if and only if J is an R-subalgebra. A number of concrete closed subalgebras of a homogeneous Banach algebra therefore are R-subalgebras. For the definition of P(A) and that of an R-subalgebra, see the introduction in Section 1. (II) We give sufficient and necessary conditions for a closed subalgebra of Lp(G), 1 ≦ p ≦ ∞, to be an R-subalgebra.

MSC classification

Secondary: 43A15: $L^p$-spaces and other function spaces on groups, semigroups, etc. 43A45: Spectral synthesis on groups, semigroups, etc. 46J30: Subalgebras
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 29 , Issue 4 , June 1980 , pp. 407 - 416
Copyright
Copyright © Australian Mathematical Society 1980

References

Edwares, R. E. (1967), Fourier series, a modern introduction, II (Holt, Reinhart and Winston, Inc., New York).Google Scholar
Frisdberg, S. (1970), ‘Closed subalgebras of group algebras’, Trans. Amer. Math. Soc. 147, 117–125.CrossRefGoogle Scholar
Kahane, J. P. (1965), ‘Idempotents and closed subalgebras of A(Z)’, in On function algebras, pp. 198–207 (Proc. Inteernat. Sympt., Tulane University).Google Scholar
Reiter, H. (1968), Classical harmonic analysis and locally compact groups (Oxford mathematics monographs, Oxford University Press, Oxford).Google Scholar
Reiter, H. (1971), L1-algebras and Segal algebras (Lecture Notes in Mathematics 231, Springer-Verlag, Berlin).CrossRefGoogle Scholar
Rider, D. (1969), ‘Closed subalgebras of L 1(T)’, Duke Math. J. 36, 105–116.CrossRefGoogle Scholar
Rudin, W. (1962), Fourier analysis on groups (Interscience, New York).Google Scholar
Šilov, G. E. (1954), ‘Homogeneous rings of functions’, in Translations, pp. 393–455 (Series 1, Volume 8, Amer. Math. Soc.).Google Scholar
Tseng, C. N. and Wang, H. C. (1975), ‘Closed subalgebras of homogeneous Banach algebras’, J. Austral. Math. Soc. Ser. A 20, 366–376.CrossRefGoogle Scholar
Wang, H. C. (1972), ‘Nonfactorization in group algebras’. Studia Math. 42, 231–241.CrossRefGoogle Scholar
Wang, H. C. (1977), Homogeneous Banach algebras (Lecture Notes in Pure and Applied mathematics 29, Marcel Dekker, Inc., New York).Google Scholar