Hostname: page-component-669899f699-rg895 Total loading time: 0 Render date: 2025-04-25T22:38:23.815Z Has data issue: false hasContentIssue false
  • English
  • Français

THE PRODUCT OF A GENERALIZED QUATERNION GROUP AND A CYCLIC GROUP

Part of: Representation theory of groups Permutation groups

Published online by Cambridge University Press:  11 November 2024

SHAOFEI DU ,
WENJUAN LUO  and
HAO YU Open the ORCID record for HAO YU [Opens in a new window]
SHAOFEI DU
Affiliation:
Capital Normal University, School of Mathematical Sciences, Beijing 100048, PR China e-mail: [email protected]
WENJUAN LUO
Affiliation:
Capital Normal University, School of Mathematical Sciences, Beijing 100048, PR China e-mail: [email protected]
HAO YU*
Affiliation:
Capital Normal University, School of Mathematical Sciences, Beijing 100048, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 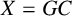$X=GC$ be a group, where C is a cyclic group and G is either a generalized quaternion group or a dihedral group such that 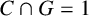$C\cap G=1$. In this paper, X is characterized and, moreover, a complete classification for 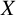$X$ is given, provided that G is a generalized quaternion group and C is core-free.

Keywords

factorizations of groupsgeneralized quaternion groupdihedral groupregular Cayley mapskew morphism

MSC classification

Primary: 20D40: Products of subgroups
Secondary: 20B05: General theory for finite groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 118 , Issue 1 , February 2025 , pp. 31 - 64
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work is supported in part by the National Natural Science Foundation of China (12071312).

Communicated by Michael Giudici

References

Amberg, B., Franciosi, S. and de Giovanni, F., Products of Groups (Oxford University Press, New York, 1992).CrossRefGoogle Scholar
Amberg, B. and Kazarin, L., ‘Factorizations of groups and related topics’, Sci. China Ser. A 52(2) (2009), 217–230.CrossRefGoogle Scholar
Douglas, J., ‘On the supersolvability of bicyclic groups’, Proc. Natl. Acad. Sci. USA 47 (1961), 1493–1495.CrossRefGoogle ScholarPubMed
Du, S. F., Luo, W. J. and Yu, H., ‘The product of a generalized quaternion group and a cyclic group’, Preprint, 2023, arXiv:2305.08617.CrossRefGoogle Scholar
Du, S. F., Malnič, A. and Marušič, D., ‘Classification of 2-arc-transitive dihedrants’, J. Combin. Theory Ser. B 98(6) (2008), 1349–1372.CrossRefGoogle Scholar
Du, S. F. and Zhang, J. Y., ‘On the skew-morphisms of dihedral groups’, J. Group Theory 19 (2016), 993–1016.Google Scholar
Gaschütz, W., ‘Zur Erweiterunstheorie endlicher Gruppen’, J. Math. 190 (1952), 93–107.Google Scholar
Hu, K., Kovács, I. and Kwon, Y. S., ‘Classification of skew morphisms of dihedral groups’, J. Group Theory 26(3) (2023), 547–569.Google Scholar
Hu, K. and Ruan, D. Y., ‘Smooth skew morphisms of dicyclic groups’, J. Algebraic Combin. 56 (2022), 1119–1134.CrossRefGoogle Scholar
Huppert, B., Endliche Gruppen. I (Springer, Berlin, 1967).CrossRefGoogle Scholar
Itô, N., ‘Über das Produkt von zwei abelschen Gruppen’, Math. Z. 62 (1955), 400–401.CrossRefGoogle Scholar
Jajcay, R. and Širáň, J., ‘Skew-morphisms of regular Cayley maps’, Discrete Math. 224(2002), 167–179.CrossRefGoogle Scholar
Kegel, O. H., ‘Produkte nilpotenter Gruppen’, Arch. Math. 12 (1961), 90–93.CrossRefGoogle Scholar
Kovács, I. and Kwon, Y. S., ‘Regular Cayley maps for dihedral groups’, J. Combin. Theory Ser. B 148 (2021), 84–124.CrossRefGoogle Scholar
Li, C. H. and Xia, B. Z., ‘Factorizations of almost simple groups with a solvable factor, and Cayley graphs of solvable groups’, Mem. Amer. Math. Soc. 279(1375) (2022), v+99 pages.Google Scholar
Lucchini, A., ‘On the order of transitive permutation groups with cyclic point-stabilizer’, Atti. Accad. Naz. Lincei CI. Sci. Fis. Mat. Natur. Rend. Lincei (9) Mat. Appl. 9 (1998), 241–243.Google Scholar
Monakhov, V. S., ‘The product of two groups, one of which contains a cyclic subgroup of index $\le 2$ ’, Mat. Zametki 16 (1974), 285–295.Google Scholar
Suzuki, M., Group Theory. I (Springer, Berlin, 1982).CrossRefGoogle Scholar
Wielandt, H., ‘Über Produkte von nilpotenter Gruppen’, Illinois J. Math. 2 (1958), 611–618.CrossRefGoogle Scholar
Wielandt, H., Finite Permutation Groups (Academic Press, New York, 1964).Google Scholar