Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dumir, Vishwa Chander
1969.
Asymmetric inequality for non-homogeneous ternary quadratic forms.
Journal of Number Theory,
Vol. 1,
Issue. 3,
p.
326.
Hans-Gill, R. J.
and
Raka, Madhu
1979.
Inhomogeneous minimum of indefinite quadratic forms in five variables of type (3,2) or (2,3): A conjecture of watson.
Monatshefte f�r Mathematik,
Vol. 88,
Issue. 4,
p.
305.
Gruber, Peter M.
1979.
Contributions to Geometry.
p.
186.
Hans-Gill, R. J.
and
Raka, Madhu
1980.
Positive values of inhomogeneous 5-ary quadratic forms of type (3, 2).
Journal of the Australian Mathematical Society,
Vol. 29,
Issue. 4,
p.
439.
Hans-Gill, R. J.
and
Raka, Madhu
1981.
Positive values of inhomogeneous quinary quadratic forms of type (4,1).
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 31,
Issue. 2,
p.
175.
Bambah, R.P
Dumir, V.C
and
Hans-Gill, R.J
1983.
On a conjecture of Jackson on non-homogeneous quadratic forms.
Journal of Number Theory,
Vol. 16,
Issue. 3,
p.
403.
Aggarwal, Satish K.
and
Gupta, D.P.
1991.
Least positive value of non-homogeneous indefinite quadratic forms of signature −3.
Journal of Number Theory,
Vol. 37,
Issue. 3,
p.
260.
Dumir, V C
and
Sehmi, Ranjeet
1994.
Positive values of non-homogeneous indefinite quadratic forms of type (1,4).
Proceedings Mathematical Sciences,
Vol. 104,
Issue. 3,
p.
557.
Bambah, R. R.
Dumir, V. C.
and
Hans-Gill, R. J.
2000.
Number Theory.
p.
15.
Bambah, R. P.
Dumir, V. C.
and
Hans-Gill, R. J.
2000.
Number Theory.
p.
15.
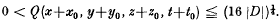 Equality is necessary if and only if either
Equality is necessary if and only if either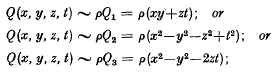 where ρ ≠ 0. For Q1 equality occurs if and only if
where ρ ≠ 0. For Q1 equality occurs if and only if 