Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ormerod, Elizabeth A.
1974.
Proceedings of the Second International Conference on the Theory of Groups.
Vol. 372,
Issue. ,
p.
541.
Bryce, R. A.
1974.
Proceedings of the Second International Conference on the Theory of Groups.
Vol. 372,
Issue. ,
p.
150.
Ormerod, Elizabeth A.
1974.
Some abelian-by-nilpotent varieties of p-groups.
Bulletin of the Australian Mathematical Society,
Vol. 11,
Issue. 3,
p.
467.
Ormerod, Elizabeth A.
1974.
Proceedings of the Second International Conference on the Theory of Groups.
Vol. 372,
Issue. ,
p.
541.
Bryce, R. A.
1974.
Proceedings of the Second International Conference on the Theory of Groups.
Vol. 372,
Issue. ,
p.
150.
Noskov, G. A.
Remeslennikov, V. N.
and
Roman'kov, V. A.
1982.
Infinite groups.
Journal of Soviet Mathematics,
Vol. 18,
Issue. 5,
p.
669.
Krop, Leonid
1986.
On the representations of the full matrix semigroup on homogeneous polynomials.
Journal of Algebra,
Vol. 99,
Issue. 2,
p.
370.


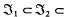 …, and an arbitrary proper subvariety
…, and an arbitrary proper subvariety 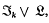 , where
, where 