Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T14:12:39.008Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Stone-Čech bicompactification of a bispace

Part of: Maps and general types of spaces defined by maps Fairly general properties Spaces with richer structures

Published online by Cambridge University Press:  09 April 2009

S. Garcia-Ferreira ,
S. Romaguera  and
M. Sanchis
S. Garcia-Ferreira
Affiliation:
Instituto de Mathemáticas, Ciudad Universitaria (UNAM), 04510, México D.F., México e-mail: [email protected]
S. Romaguera
Affiliation:
Escuela de Caminos, Departamento de Matemática Aplicada, Universidad Politécnica de Valencia, 46071 Valencia, Spain e-mail: [email protected]
M. Sanchis
Affiliation:
Department de Mathemàtiques, Universitat Jaume I, Campus del Riu Sec, 12071 Castelló, Spain e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

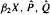In this paper we study the Stone-Čech bicompactification () of the bispace (X, P, Q). We show that the ring of all continuous real-valued functions on (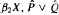) may be identified with the uniform closure of a suitable subring of 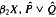C(). Using this result, we give a characterization of the Wallman-Sanin compactifications of the pairwise Tychonoff bitopological spaces.

Keywords

BispaceWallman-Sanin compactificationStone-Čech bicompactificationequivalent compactificationsbicontinuous function

MSC classification

Secondary: 54C20: Extension of maps 54C30: Real-valued functions 54D35: Extensions of spaces (compactifications, supercompactifications, completions, etc.) 54E50: Complete metric spaces 54E55: Bitopologies
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 66 , Issue 3 , June 1999 , pp. 358 - 372
Copyright
Copyright © Australian Mathematical Society 1999

References

[BY]Ball, B. J. and Yokura, S., ‘Compactifications determined by subsets of C*(X), II’, Topol. Appl. 15 (1983), 1–6.Google Scholar
[Bi]Birsan, T., ‘Compacité dans les espaces bitopologiques’, An. Sti. Univ. Al. I. Cuza, Mat. 15 (1969), 317–328.Google Scholar
[Bl]Blasco, J. L., ‘Hausdorff compactifications and Lebesgue sets’, Topol. Appl. 15 (1993), 111–117.CrossRefGoogle Scholar
[CV]Caterino, A. and Vipera, M. C., ‘Weight of a compactification and generating sets of functions’, Rend. Sem. Math. Univ. Padova 79 (1988), 37–47.Google Scholar
[Cha]Chandler, R. E., Hausdorff compactifications, Lecture Notes in Pure and Appl. Math., vol. 23 (Marcel Dekker, 1976).Google Scholar
[En]Engelking, R., General topology (PWN, Warsaw, 1977).Google Scholar
[FHP]Fletcher, P., Hoyle, H. B. III and Patty, C. W., ‘The comparison of topologies’, Duke Math. J. 36 (1969), 325–331.Google Scholar
[GJ]Gillman, L. and Jerison, J., Rings of continuous functions (Van Nostrand Reinhold, New York, 1960).Google Scholar
[Ke]Kelley, J. C., ‘Bitopological spaces’, Proc. London Math. Soc. 13 (1963), 71–89.CrossRefGoogle Scholar
[Ki]Kim, Y. W., ‘Pairwise compactness’, Publ. Math. Debrecen 15 (1968), 87–90.Google Scholar
[La]Lane, E. P., ‘Bitopological spaces and quasi-uniform spaces’, Proc. London Math. Soc. 17 (1967), 341–356.Google Scholar
[Na]Nagata, J., Modern general topology (North-Holland, Amsterdam, 1968).Google Scholar
[Sae]Saegrove, M. J., ‘Pairwise complete regularity and compactification’, J. London Math. Soc. 7 (1973), 286–290.Google Scholar
[Sa1]Salbany, S., Bitopological spaces, compactifications and completions (Ph.D. Thesis, Univ. Cape Town, 1970).Google Scholar
[Sa2]Salbany, S., ‘A bitopological view of topology and order’, in: Categorical Topology (Proc. Toledo, Ohio, 1983) (Heldermann, 1984) pp. 481–504.Google Scholar
[St]Steiner, E. F., ‘Normal families and completely regular spaces’, Duke Math. J. 33 (1966), 743–746.Google Scholar
[Sw]Swart, J., ‘Total disconnectedness in bitopological spaces and product of bitopological spaces’, Proc. Kon. Ned. Akad. v. Wetensch. 74 (1971), 135–145.CrossRefGoogle Scholar
[Ta]Taǐmanov, A. D., ‘On the extension of continuous mappings of topological spaces’, Mat. Sb. 31 (1952), 459–462 (Russian).Google Scholar