No CrossRef data available.
Article contents
On the semigroup of bounded C1-mappings
Published online by Cambridge University Press: 09 April 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let E be a real Banach space. If f: E→E is (Fréchet-) differentiable at every point of E, the derivative of f at x is denoted by f'(x), which is an element of the Banach algebra ℒ=ℒ(E) of all linear continuous mappings of E into itself with the usual upper bound norm, and, if we put 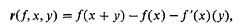 , we have
, we have 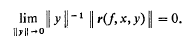 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1973
References
[2]Bochner, S. and Montgomery, D., ‘Groups of differentiable transformations’, Ann. Math. 45 (1945), 685–694.CrossRefGoogle Scholar
[4]Dorroh, J. R., ‘Semigroups of non–linear transformation,’ Michigan Math. J., 12 (1965) 317–320.CrossRefGoogle Scholar
[5]Eells, J. Jr, ‘A setting for global analysis’, Bull. Amer. Math. Soc. 72 (1966), 751–807.CrossRefGoogle Scholar
[6]Eidelheit, M., ‘On isomorphisms of rings of linear operators,’ Studia Math. 9 (1950), 97–105.CrossRefGoogle Scholar
[7]Magill, K. D. Jr, ‘Automorphisms of the semigroup of all differentiable functions’, Glasgow Math. J. 8 (1967), 63–66.CrossRefGoogle Scholar
[8]Yamamuro, S., ‘On the semigroup of differentiable mappings,’ J. Australian Math. Soc. 10 (1969), 503–510.CrossRefGoogle Scholar


