No CrossRef data available.
Article contents
On the construction of convergent iterative sequences of polynomials
Published online by Cambridge University Press: 09 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We answer two conjectures suggested by Zalman Rubinstein. We prove his Conjecture 1, that is, we construct convergent iterative sequences for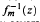 
with an arbitrary initial point, where 
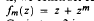with m ≥ 2. We also show by several counterexamples that Rubinstein's Conjecture 2 is generally false.
MSC classification
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 47 , Issue 3 , December 1989 , pp. 382 - 390
- Copyright
- Copyright © Australian Mathematical Society 1989
References
[1]Rubinstein, Zalman, ‘A variational method for the construction of convergent iterative sequences’, J. Austral. Math. Soc. Ser. A 41 (1986), 51–58.CrossRefGoogle Scholar
[2]Brolin, H., ‘Invariant sets under iteration of rational functions’, Ark. Mat. 6 (1965), 103–144.CrossRefGoogle Scholar
[3]Fatou, P., ‘Sur les équations fonctionelles’, Bull. Soc. Math. France 47 (1919), 161–271.CrossRefGoogle Scholar
[4]Fatou, P., ‘Sur l'itération des fonctions transcendantes entieres’, Acta Math. 47 (1926), 337–370.CrossRefGoogle Scholar
[5]Julia, G., ‘Memoire sur l'itération des fonctions rationnelles’, J. Math. Pures Appl. (8) 1 (1918), 47–245.Google Scholar
[6]Baker, I. N., ‘Permutable power series and regular iteration’, J. Austral. Math. Soc. 2 (1962), 265–194.CrossRefGoogle Scholar
[7]Seigel, C., ‘Iteration of analtyic functions’, Ann. of Math. (2) 43 (1942), 607–612.CrossRefGoogle Scholar
You have
Access