Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-23T02:55:14.672Z Has data issue: false hasContentIssue false
  • English
  • Français

On ergodic theorem for a Banach valued random sequence

Published online by Cambridge University Press:  09 April 2009

Zoran R. Pop-Stojanovic
Zoran R. Pop-Stojanovic
Affiliation:
University of Florida, Gainesville,
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we shall deal with a probability space (S, Σ, P), a separable Banach space X having its strong dual X* and a strictly stationary random sequence 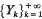defined as in [7], where 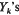are X-valued, Gelfand-Pettis (weakly) integrable [6], [9], and strongly measurable random variables. In the case when Yk's are Bochner (strongly) integrable random variables one can find the ergodic theorem for such a sequence and, with respect to strong convergence in X, in the papers [7], [8].

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 13 , Issue 4 , June 1972 , pp. 501 - 507
Copyright
Copyright © Australian Mathematical Society 1972

References

[1]Banach, S., Théorie des Opérations Linéaires (Chelsea Publishing Company, New York).Google Scholar
[2]Birkhoff, G. D., ‘Proof of the Ergodic theorem’, Proc. Nat. Acad. Sci., U.S.A. 17 (1931), 656–660.CrossRefGoogle ScholarPubMed
[3]Brooks, J. K., ‘Representations of weak and strong integrals in Banach spaces,’ Proc. Nat. Acad. Sci., U.S.A. 63 (1969), 266–270.CrossRefGoogle ScholarPubMed
[4]Chatterji, S. D., ‘A note on the convergence of Banach valued martingales’, Math. Ann. 153 (1964), 142–149.CrossRefGoogle Scholar
[5]Day, M. M., Normed linear spaces (Springer-Verlag, Berlin (1958)).CrossRefGoogle Scholar
[6]Gelfand, I., ‘Sur un lemme de la théorie des espaces linéaires’, Comm. Inst. Math. de Kharkoff (4) 13 (1936), 35–40.Google Scholar
[7]Mourier, E., Eléments aléatoires à valeurs dans un espace de Banach (Gauthier Villars, Paris (1954)).Google Scholar
[8]Parthasarathy, K. R., Probability Measures on Metric Spaces (Academic Press, New York (1967)).CrossRefGoogle Scholar
[9]Pettis, B. J., ‘On integration in vector spaces’, Trans. Amer. Math. Soc. 44 (1938), 277–304.CrossRefGoogle Scholar
[10]Scalora, F. S., ‘Abstract Martingale Convergence Theorems’, Pac. J. of Math. II (1961), 347–374.CrossRefGoogle Scholar