Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Haukkanen, Pentti
1988.
A Note on Specially Multiplicative Arithmetic Functions.
The Fibonacci Quarterly,
Vol. 26,
Issue. 4,
p.
325.
Puchta, Jan-Christoph
and
Spilker, J�rgen
1995.
Faltungen von vollst�ndig multipiikativen Funktionen.
Archiv der Mathematik,
Vol. 65,
Issue. 6,
p.
516.
MacHenry, Trueman
1999.
A Subgroup of the Group of Units in the Ring of Arithmetic Functions.
Rocky Mountain Journal of Mathematics,
Vol. 29,
Issue. 3,
Elliott, Jesse
2006.
Binomial rings, integer-valued polynomials, and λ-rings.
Journal of Pure and Applied Algebra,
Vol. 207,
Issue. 1,
p.
165.
Elliott, Jesse
2008.
Ring structures on groups of arithmetic functions.
Journal of Number Theory,
Vol. 128,
Issue. 4,
p.
709.
Haukkanen, Pentti
Ilmonen, Pauliina
Nalli, Ayse
and
Sillanpää, Juha
2010.
On unitary analogs of GCD reciprocal LCM matrices.
Linear and Multilinear Algebra,
Vol. 58,
Issue. 5,
p.
599.
Machenry, Trueman
and
Wong, Kieh
2012.
A correspondence between the isobaric ring and multiplicative arithmetic functions.
Rocky Mountain Journal of Mathematics,
Vol. 42,
Issue. 4,
TÓTH, LÁSZLÓ
2013.
TWO GENERALIZATIONS OF THE BUSCHE–RAMANUJAN IDENTITIES.
International Journal of Number Theory,
Vol. 09,
Issue. 05,
p.
1301.
Li, Huilan
and
Machenry, Trueman
2013.
The convolution ring of arithmetic functions and symmetric polynomials.
Rocky Mountain Journal of Mathematics,
Vol. 43,
Issue. 4,
Tóth, László
2014.
Mathematics Without Boundaries.
p.
483.
Li, Huilan
MacHenry, Trueman
and
Conci, Aura
2017.
Rational convolution roots of isobaric polynomials.
Rocky Mountain Journal of Mathematics,
Vol. 47,
Issue. 4,
Haukkanen, Pentti
2024.
Some properties of totients.
The Ramanujan Journal,
Vol. 65,
Issue. 2,
p.
885.
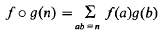 for all n∈Z+. Recall that the set of all multiplicative functions, denoted by M, with this operation is an abelian group.
for all n∈Z+. Recall that the set of all multiplicative functions, denoted by M, with this operation is an abelian group.