Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-22T02:19:01.682Z Has data issue: false hasContentIssue false
  • English
  • Français

MÖBIUS INVARIANT FUNCTION SPACES AND DIRICHLET SPACES WITH SUPERHARMONIC WEIGHTS

Part of: Spaces and algebras of analytic functions Function theory on the disc Other generalizations

Published online by Cambridge University Press:  12 July 2018

GUANLONG BAO ,
JAVAD MASHREGHI ,
STAMATIS POULIASIS  and
HASI WULAN
GUANLONG BAO
Affiliation:
Department of Mathematics, Shantou University, Shantou, Guangdong 515063, China email [email protected]
JAVAD MASHREGHI
Affiliation:
Département de Mathématiques et de Statistique, Université Laval, 1045 avenue de la Médecine, Québec, QC G1V 0A6, Canada email [email protected]
STAMATIS POULIASIS*
Affiliation:
Department of Mathematics, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece
HASI WULAN
Affiliation:
Department of Mathematics, Shantou University, Shantou, Guangdong 515063, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 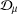${\mathcal{D}}_{\unicode[STIX]{x1D707}}$ be Dirichlet spaces with superharmonic weights induced by positive Borel measures 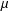$\unicode[STIX]{x1D707}$ on the open unit disk. Denote by 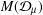$M({\mathcal{D}}_{\unicode[STIX]{x1D707}})$ Möbius invariant function spaces generated by 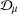${\mathcal{D}}_{\unicode[STIX]{x1D707}}$. In this paper, we investigate the relation among 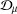${\mathcal{D}}_{\unicode[STIX]{x1D707}}$, 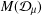$M({\mathcal{D}}_{\unicode[STIX]{x1D707}})$ and some Möbius invariant function spaces, such as the space 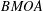$BMOA$ of analytic functions on the open unit disk with boundary values of bounded mean oscillation and the Dirichlet space. Applying the relation between 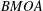$BMOA$ and 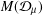$M({\mathcal{D}}_{\unicode[STIX]{x1D707}})$, under the assumption that the weight function 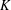$K$ is concave, we characterize the function 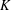$K$ such that 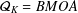${\mathcal{Q}}_{K}=BMOA$. We also describe inner functions in 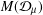$M({\mathcal{D}}_{\unicode[STIX]{x1D707}})$ spaces.

Keywords

Möbius invariant function spacesDirichlet spaces with superharmonic weightsinner functions

MSC classification

Primary: 30H25: Besov spaces and $Q_p$-spaces
Secondary: 30J05: Inner functions 31C25: Dirichlet spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 106 , Issue 1 , February 2019 , pp. 1 - 18
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

G. Bao and H. Wulan were supported by the NNSF of China (No. 11720101003). G. Bao was also supported by the STU Scientific Research Foundation for Talents (No. NTF17020).

†

Current address: Department of Mathematics and Statistics, Texas Tech University, Lubbock, Texas 79409, USA [email protected]

References

Aleman, A., ‘Hilbert spaces of analytic functions between the Hardy and the Dirichlet space’, Proc. Amer. Math. Soc. 115 (1992), 97–104.Google Scholar
Aleman, A., ‘The multiplication operator on Hilbert spaces of analytic functions’, Habilitation, FernUniversität in Hagen, 1993.Google Scholar
Aleman, A. and Simbotin, A., ‘Estimates in Möbius invariant spaces of analytic functions’, Complex Var. Theory Appl. 49 (2004), 487–510.Google Scholar
Arazy, J., Fisher, S. and Peetre, J., ‘Möbius invariant function spaces’, J. reine angew. Math. 363 (1985), 110–145.Google Scholar
Armitage, D. H. and Gardiner, S. J., Classical Potential Theory, Springer Monographs in Mathematics (Springer, London, 2001).Google Scholar
Aulaskari, R. and Lappan, P., ‘Criteria for an analytic function to be Bloch and a harmonic or meromorphic function to be normal’, in: Complex Analysis and its Applications, Pitman Research Notes in Mathematics, 305 (Longman Scientific and Technical, Harlow, 1994), 136–146.Google Scholar
Aulaskari, R., Xiao, J. and Zhao, R., ‘On subspaces and subsets of BMOA and UBC ’, Analysis 15 (1995), 101–121.Google Scholar
Axler, S., ‘The Bergman space, the Bloch space, and commutators of multiplication operators’, Duke Math. J. 53 (1986), 315–332.Google Scholar
Baernstein, A., Analytic Functions of Bounded Mean Oscillation, Aspects of Contemporary Complex Analysis (Academic Press, London–New York, 1980), 3–36.Google Scholar
Bao, G., Göğüş, N. G. and Pouliasis, S., ‘On Dirichlet spaces with a class of superharmonic weights’, Canad. J. Math. doi:10.4153/CJM-2017-005-1.Google Scholar
Bao, G., Göğüş, N. G. and Pouliasis, S., ‘𝓠 p spaces and Dirichlet type spaces’, Canad. Math. Bull. 60 (2017), 690–704.Google Scholar
Bao, G., Lou, Z., Qian, R. and Wulan, H., ‘Improving multipliers and zero sets in 𝓠 K spaces’, Collect. Math. 66 (2015), 453–468.Google Scholar
Carleson, L., ‘An interpolation problem for bounded analytic functions’, Amer. J. Math. 80 (1958), 921–930.Google Scholar
Carleson, L., ‘Interpolation by bounded analytic functions and the corona problem’, Ann. of Math. 76 (1962), 547–559.Google Scholar
Duren, P. L., Theory of H p Spaces (Academic Press, New York–London, 1970). Reprinted with supplement by Dover Publications, Mineola, New York, 2000.Google Scholar
Duren, P. L. and Schuster, A., ‘Finite unions of interpolation sequences’, Proc. Amer. Math. Soc. 130 (2002), 2609–2615.Google Scholar
El-Fallah, O., Kellay, K., Klaja, H., Mashreghi, J. and Ransford, T., ‘Dirichlet spaces with superharmonic weights and de Branges–Rovnyak spaces’, Complex Anal. Oper. Theory 10 (2016), 97–107.Google Scholar
Essén, M. and Wulan, H., ‘On analytic and meromorphic functions and spaces of 𝓠 K -type’, Illinois J. Math. 46 (2002), 1233–1258.Google Scholar
Essén, M., Wulan, H. and Xiao, J., ‘Several function-theoretic characterizations of Möbius invariant 𝓠 K spaces’, J. Funct. Anal. 230 (2006), 78–115.Google Scholar
Essén, M. and Xiao, J., ‘Some results on 𝓠 p spaces, 0 < p < 1’, J. reine angew. Math. 485 (1997), 173–195.Google Scholar
Garnett, J. B., Bounded Analytic Functions. Revised 1st edn, Graduate Texts in Mathematics, 236 (Springer, 2007).Google Scholar
Girela, D., ‘Analytic functions of bounded mean oscillation’, in: Complex Function Spaces, Mekrijärvi, 1999, Department of Mathematics Report Series, 4 (ed. Aulaskari, R.) (University of Joensuu, Joensuu, 2001), 61–170.Google Scholar
Gorkin, P. and Mortini, R., ‘Two new characterizations of Carleson–Newman Blaschke products’, Israel J. Math. 177 (2010), 267–284.Google Scholar
McDonald, G. and Sundberg, C., ‘Toeplitz operators on the disc’, Indiana Univ. J. Math. 28 (1979), 595–611.Google Scholar
Pau, J. and Peláez, J., ‘On the zeros of functions in Dirichlet-type spaces’, Trans. Amer. Math. Soc. 363 (2011), 1981–2002.Google Scholar
Richter, S., ‘A representation theorem for cyclic analytic two-isometries’, Trans. Amer. Math. Soc. 328 (1991), 325–349.Google Scholar
Rubel, L. and Timoney, R., ‘An extremal property of the Bloch space’, Proc. Amer. Math. Soc. 75 (1979), 45–49.Google Scholar
Wulan, H. and Zhu, K., Möbius Invariant 𝓠 K Spaces (Springer, Cham, 2017).Google Scholar
Xiao, J., ‘Some essential properties of 𝓠 p (∂𝛥)-spaces’, J. Fourier Anal. Appl. 6 (2000), 311–323.Google Scholar
Xiao, J., Holomorphic 𝓠 Classes, Lecture Notes in Mathematics, 1767 (Springer, Berlin, 2001).Google Scholar
Xiao, J., Geometric 𝓠 p Functions (Birkhäuser, Basel–Boston–Berlin, 2006).Google Scholar
Zhou, J. and Bao, G., ‘Analytic version of 𝓠1(∂D) space’, J. Math. Anal. Appl. 422 (2015), 1091–1102.Google Scholar
Zhu, K., Operator Theory in Function Spaces (American Mathematical Society, Providence, RI, 2007).Google Scholar
Zhu, K., ‘A class of Möbius invariant function spaces’, Illinois J. Math. 51 (2007), 977–1002.Google Scholar