Article contents
Minimum determinant of asymmetric quadratic forms
Published online by Cambridge University Press: 09 April 2009
Extract
Let f = f (x1, x2,… xn) be an indefinite n-ary quadratic form of signature s and let m+(f), m−(f) denote the infimum of the non-negative values taken by f and —f respectively for integral (x1, x2,…, xn) ≠ (0, 0,…, 0). Furthermore let f satisfy the condition m+ (f) ≠ 0 and let 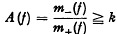 for some integer k. Then Segré [3] has shown that, for n = 2, f must have determinant det (f) satisfying
for some integer k. Then Segré [3] has shown that, for n = 2, f must have determinant det (f) satisfying 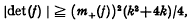 with equality if and only if f is equivalent under an integral unimodular transformation (denoted ˜) to a multiple of the form f1(x, y) = x2−kxy−ky2, while Oppenheim [2] has shown that, for n ≧ 3,
with equality if and only if f is equivalent under an integral unimodular transformation (denoted ˜) to a multiple of the form f1(x, y) = x2−kxy−ky2, while Oppenheim [2] has shown that, for n ≧ 3,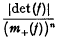 is of the order of k2n−2
is of the order of k2n−2
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1967
References
- 4
- Cited by


