Article contents
Locally soluble groups with min-n.
Published online by Cambridge University Press: 09 April 2009
Extract
It was shown by Baer in [1] that every soluble group satisfying Min-n, the minimal condition for normal subgroups, is a torsion group. Examples of non-soluble locally soluble groups satisfying Min-n have been known for some time (see McLain [2]), and these examples too are periodic. This raises the question whether all locally soluble groups with Min-n are torsion groups. We prove here that this is not the case, by establishing the existence of non-trivial locally soluble torsion-free groups satisfying Min-n. Rather than exhibiting one such group G, we give a general method for constructing examples; the reader will then be able to see that a variety of additional conditions may be imposed on G. It will follow, for instance, that G may be a Hopf group whose normal subgroups are linearly ordered by inclusion and are all complemented in G; further, that the countable groups G with these properties fall into exactly 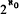 isomorphism classes. Again, there are exactly
isomorphism classes. Again, there are exactly 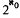 isomorphism classes of countable groups G which have hypercentral nonnilpotent Hirsch-Plotkin radical, and which at the same time are isomorphic to all their non-trivial homomorphic images.
isomorphism classes of countable groups G which have hypercentral nonnilpotent Hirsch-Plotkin radical, and which at the same time are isomorphic to all their non-trivial homomorphic images.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1974
References
- 10
- Cited by


