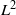Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T03:02:14.629Z Has data issue: false hasContentIssue false
  • English
  • Français

THE ${L}^{2} $-SINGULAR DICHOTOMY FOR EXCEPTIONAL LIE GROUPS AND ALGEBRAS

Part of: Abstract harmonic analysis Calculus on manifolds; nonlinear operators Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  24 July 2013

K. E. HARE ,
D. L. JOHNSTONE ,
F. SHI  and
W.-K. YEUNG
K. E. HARE*
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario, Canada N2L 3G1 email [email protected]
D. L. JOHNSTONE
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario, Canada N2L 3G1 email [email protected]
F. SHI
Affiliation:
Department of Mathematics, Chinese University of Hong Kong, Shatin, Hong Kong email [email protected]@hotmail.com
W.-K. YEUNG
Affiliation:
Department of Mathematics, Chinese University of Hong Kong, Shatin, Hong Kong email [email protected]@hotmail.com
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that every orbital measure, 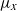${\mu }_{x} $, on a compact exceptional Lie group or algebra has the property that for every positive integer either 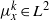${ \mu }_{x}^{k} \in {L}^{2} $ and the support of 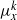${ \mu }_{x}^{k} $ has non-empty interior, or 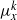${ \mu }_{x}^{k} $ is singular to Haar measure and the support of 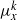${ \mu }_{x}^{k} $ has Haar measure zero. We also determine the index 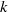$k$ where the change occurs; it depends on properties of the set of annihilating roots of $x$. This result was previously established for the classical Lie groups and algebras. To prove this dichotomy result we combinatorially characterize the subroot systems that are kernels of certain homomorphisms.

Keywords

exceptional Lie group/algebraroot systemorbital measureadjoint orbitconjugacy class

MSC classification

Secondary: 43A80: Analysis on other specific Lie groups 17B22: Root systems 58C35: Integration on manifolds; measures on manifolds
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 95 , Issue 3 , December 2013 , pp. 362 - 382
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Dooley, A. H., Repka, J. and Wildberger, N. J., ‘Sums of adjoint orbits’, Linear Multilinear Algebra 36 (1993), 79–101.CrossRefGoogle Scholar
Dooley, A. H. and Wildberger, N. J., ‘Harmonic analysis and the global exponential map for compact Lie groups’, Funct. Anal. Appl. 27 (1993), 21–27.CrossRefGoogle Scholar
Frumkin, A. and Goldberger, A., ‘On the distribution of the spectrum of the sum of two Hermitian or real symmetric matrices’, Adv. Appl. Math. 37 (2006), 268–286.CrossRefGoogle Scholar
Gupta, S. K. and Hare, K. E., ‘${L}^{2} $-singular dichotomy for orbital measures of classical simple Lie algebras of classical compact Lie groups’, Adv. Math. 222 (2009), 1521–1573.CrossRefGoogle Scholar
Gupta, S. K., Hare, K. E. and Seyfaddini, S., ‘${L}^{2} $-singular dichotomy for orbital measures of classical simple Lie algebras’, Math Z. 262 (2009), 91–124.CrossRefGoogle Scholar
Hare, K. and Skoufranis, P., ‘The smoothness of orbital measures on exceptional Lie groups and algebras’, J. Lie Theory 21 (2011), 987–1007.Google Scholar
Hare, K. E. and Yeats, K., ‘Size of characters of exceptional Lie groups’, J. Aust. Math. Soc. 77 (2004), 1–16.CrossRefGoogle Scholar
Humphreys, J. E., Introduction to Lie Algebras and Representation Theory (Springer, New York, 1994).Google Scholar
Kane, R., Reflection Groups and Invariant Theory, CMS Books in Math. 5 (Springer, New York, 2001).CrossRefGoogle Scholar
Knapp, A., Lie Groups Beyond an Introduction (Birkhäuser, Boston, 1996).CrossRefGoogle Scholar
Ragozin, D. L., ‘Central measures on compact simple Lie groups’, J. Funct. Anal. 10 (1972), 212–229.CrossRefGoogle Scholar
Ricci, F. and Stein, E., ‘Harmonic analysis on nilpotent groups and singular integrals. III Fractional integration along manifolds’, J. Funct. Anal. 86 (1989), 360–389.CrossRefGoogle Scholar
Wildberger, N. J., ‘On a relationship between adjoint orbits and conjugacy classes of a Lie group’, Canad. Math. Bull. 33 (1990), 297–304.CrossRefGoogle Scholar
Wright, A., ‘Sums of adjoint orbits and ${L}^{2} $-singular dichotomy for $SU(n)$’, Adv. Math. 227 (2011), 253–266.CrossRefGoogle Scholar