Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T23:30:42.366Z Has data issue: false hasContentIssue false
  • English
  • Français

The iterated equation of generalized axially symmetric potential theory. I. Particular solutions

Published online by Cambridge University Press:  09 April 2009

J. C. Burns
J. C. Burns
Affiliation:
The Australian National University Canberra, A.C.T.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The iterated equation of generalized axially symmetric potential theory (GASPT) [1] is defined by the relations (1) where (2) 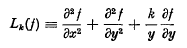and Particular cases of this equation occur in many physical problems. In classical hydrodynamics, for example, the case n = 1 appears in the study of the irrotational motion of an incompressible fluid where, in two-dimensional flow, both the velocity potential φ and the stream function Ψ satisfy Laplace's equation, L0(f) = 0; and, in axially symmetric flow, φ and satisfy the equations L1 (φ) = 0, L-1 (ψ) = 0. The case n = 2 occurs in the study of the Stokes flow of a viscous fluid where the stream function satisfies the equation L2k(ψ) = 0 with k = 0 in two-dimensional flow and k = −1 in axially symmetric flow.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 7 , Issue 3 , August 1967 , pp. 263 - 276
Copyright
Copyright © Australian Mathematical Society 1967

References

[1]Weinstein, A., ‘Generalized axially symmetric potential theory’, Bull. Amer. Math. Soc. 59 (1953), 20–28.CrossRefGoogle Scholar
[2]Weinstein, A., ‘On a class of partial differential equations of even orders’, Ann. Mat., Pura Appl. 39 (1955), 245–254.Google Scholar
[3]Payne, L. E., ‘Representation formulas for solution of a class of partial differential equations’, J. Math. and Phys. 38 (1959), 145–149.CrossRefGoogle Scholar
[4]Weinacht, R. J., Contributions to Differential Equations III (1964), 43–55.Google Scholar
[5]Milne-Thomson, L. M., ‘Hydrodynamical Images’, Proc. Cambridge Philos. Soc. 36 (1940), 246–247; or Theoretical hydrodynamics (Macmillan, 4th ed. 1960), 154.CrossRefGoogle Scholar
[6]Weinstein, A., ‘Sur une classe d'équations aux derivées partielles singulières’, Coll. Intern. du Centre Natl. de la Recherche Scientifique, La théorie des équations aux derivées partielles (1956), 179–186.Google Scholar
[7]Forsyth, A. R., A treatise on differential equations (Macmillan, 6th ed. 1943), 62.Google Scholar
[8]Huber, A., ‘Some results on generalised axially symmetric potentials’, Proc. Conf. Part. Diff. Eq., Univ. of Maryland (1955), 147–155.Google Scholar
[9]Butler, S. J. F., ‘A note on Stokes's stream function for motion with a spherical boundary’, Proc. Cambridge Philos. Soc. 49 (1953), 169–174.Google Scholar
[10]Collins, W. D., ‘A note on Stokes's stream function for the slow steady motion of a viscous fluid before plane and spherical boundaries’, Mathematika 1 (1954), 125–130.CrossRefGoogle Scholar