Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Miller, Sanford S
Mocanu, Petru T
and
Reade, Maxwell O
1975.
The Hardy classes for functions in the class MV[α, k].
Journal of Mathematical Analysis and Applications,
Vol. 51,
Issue. 1,
p.
33.
Sim, Young Jae
Kwon, Oh Sang
and
Cho, Nak Eun
2017.
Argument Properties of Analytic Functions Associated with the Fixed Coefficients.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 40,
Issue. 3,
p.
1291.


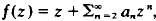 , then growth conditions for
, then growth conditions for 