Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dyer, Joan L.
and
Peter Scott, G.
1975.
Periodic automorphisms of free groups.
Communications in Algebra,
Vol. 3,
Issue. 3,
p.
195.
Hendriks, Harrie
1977.
On the existence of a free subgroup of finite index.
Journal of Pure and Applied Algebra,
Vol. 10,
Issue. 3,
p.
227.
Chiswell, I.M.
1979.
The bass-serre theorem revisited.
Journal of Pure and Applied Algebra,
Vol. 15,
Issue. 2,
p.
117.
Herrlich, Frank
1980.
Die Ordnung der Automorphismengruppe einerp-adischen Schottkykurve.
Mathematische Annalen,
Vol. 246,
Issue. 2,
p.
125.
Dyer, Joan L.
1980.
Separating conjugates in amalgamated free products and HNN extensions.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 29,
Issue. 1,
p.
35.
Herrlich, Frank
1980.
Endlich erzeugbarep-adische diskontinuierliche Gruppen.
Archiv der Mathematik,
Vol. 35,
Issue. 1,
p.
505.
Pride, Stephen J.
1980.
WORD PROBLEMS II.
Vol. 95,
Issue. ,
p.
299.
McCool, James
1980.
A characterization of periodic automorphisms of a free group.
Transactions of the American Mathematical Society,
Vol. 260,
Issue. 1,
p.
309.
Zimmermann, Bruno
1981.
Über Homöomorphismenn-dimensionaler Henkelkörper und endliche Erweiterungen von Schottky-Gruppen.
Commentarii Mathematici Helvetici,
Vol. 56,
Issue. 1,
p.
474.
Noskov, G. A.
Remeslennikov, V. N.
and
Roman'kov, V. A.
1982.
Infinite groups.
Journal of Soviet Mathematics,
Vol. 18,
Issue. 5,
p.
669.
Muller, David E.
and
Schupp, Paul E.
1983.
Groups, the Theory of ends, and context-free languages.
Journal of Computer and System Sciences,
Vol. 26,
Issue. 3,
p.
295.
Khramtsov, D. G.
1985.
Finite groups of automorphisms of free groups.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 38,
Issue. 3,
p.
721.
Khramtsov, D. G.
1987.
Finite subgroups of groups of outer automorphisms of free groups.
Algebra and Logic,
Vol. 26,
Issue. 3,
p.
217.
Autebert, Jean-Michel
Boasson, Luc
and
Sénizergues, Géraud
1987.
Groups and nts languages.
Journal of Computer and System Sciences,
Vol. 35,
Issue. 2,
p.
243.
McCullough, Darryl
and
Miller, Andy
1989.
Manifold covers of 3-orbifolds with geometric pieces.
Topology and its Applications,
Vol. 31,
Issue. 2,
p.
169.
Woess, Wolfgang
1989.
Graphs and groups with tree-like properties.
Journal of Combinatorial Theory, Series B,
Vol. 47,
Issue. 3,
p.
361.
McCullough, Darryl
Miller, Andy
and
Zimmermann, Bruno
1990.
Group actions on nonclosed 2-manifolds.
Journal of Pure and Applied Algebra,
Vol. 64,
Issue. 3,
p.
269.
McCool, James
1991.
A class of one-relator groups with centre.
Bulletin of the Australian Mathematical Society,
Vol. 44,
Issue. 2,
p.
245.
Zimmermann, Bruno
1991.
Generators and Relations in Groups and Geometries.
p.
407.
McCullough, Darryl
1991.
Virtually geometrically finite mapping class groups of 3-manifolds.
Journal of Differential Geometry,
Vol. 33,
Issue. 1,
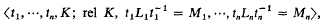 where K is a tree product of a finite number of finite groups (the vertices of K), and each (associated) subgroup Li, Mi is a subgroup of a vertex of K.
where K is a tree product of a finite number of finite groups (the vertices of K), and each (associated) subgroup Li, Mi is a subgroup of a vertex of K.