Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-04T19:42:33.559Z Has data issue: false hasContentIssue false
  • English
  • Français

Extremal problems in Hp

Part of: Commutative Banach algebras and commutative topological algebras

Published online by Cambridge University Press:  09 April 2009

Takahiko Nakazi
Takahiko Nakazi
Affiliation:
Faculty of ScienceHokkaido UniversitySapporo 060, Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 1≤p <∞ and 1/p+1/q = 1. If φ ∈ Lq, we denote by Tφ the functional defined on the Hardy space Hp by 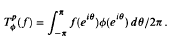. A function f in Hp, which satisfies Tpφ(f) = ‖Tpφ‖ and ‖f‖p ≤ 1, is called an extremal function. Also, φ is called an extremal kernel when ‖φ‖q =‖Tpφ‖. In this paper, using the results in the case of p = 1, we study extremal kernel and extremal functions for p > 1.

Keywords

Hardy spaceextremal problemstrong outer function

MSC classification

Secondary: 46J15: Banach algebras of differentiable or analytic functions, $H^p$-spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 52 , Issue 1 , February 1992 , pp. 103 - 110
Copyright
Copyright © Australian Mathematical Society 1992

References

[1]Abu-Muhanna, Y., ‘Support points of the unit ball of Hp(1≤p≤∞)’, Proc. Amer. Math. Soc. 89 (1983), 229–235.Google Scholar
[2]Duren, P. L., Theory of Hp Spaces, Academic Press, New York, 1970.Google Scholar
[3]Macintyre, A. J. and Rogonsinski, W. W., ‘Extremum problems in the theory of analytic functions’, Acta Math. 82 (1950), 275–325.CrossRefGoogle Scholar
[4]Nakazi, T., ‘Exposed points and extremal problems in H 1’, J. Funct. Anal. 53 (1983), 224–230.CrossRefGoogle Scholar
[5]Shapiro, H. S., ‘Regularity properties of the element of closest approximation’, Trans. Amer. Math. Soc. 181 (1973), 127–142.CrossRefGoogle Scholar