Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-06-25T23:04:33.339Z Has data issue: false hasContentIssue false
  • English
  • Français

EVALUATION FUNCTIONS AND REFLEXIVITY OF BANACH SPACES OF HOLOMORPHIC FUNCTIONS

Part of: Analytic spaces Linear function spaces and their duals Topological linear spaces and related structures

Published online by Cambridge University Press:  31 May 2024

GUANGFU CAO ,
LI HE Open the ORCID record for LI HE [Opens in a new window] ,
JI LI Open the ORCID record for JI LI [Opens in a new window]  and
SHUQING ZHANG
GUANGFU CAO
Affiliation:
School of Mathematics and Information Science, Guangzhou University, Guangzhou 510006, PR China e-mail: [email protected]
LI HE*
Affiliation:
School of Mathematics and Information Science, Guangzhou University, Guangzhou 510006, PR China
JI LI
Affiliation:
School of Mathematical and Physical Sciences, Macquarie University, Sydney, NSW 2109, Australia e-mail: [email protected]
SHUQING ZHANG
Affiliation:
School of Mathematics and Information Science, Guangzhou University, Guangzhou 510006, China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 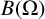$B(\Omega )$ be a Banach space of holomorphic functions on a bounded connected domain $\Omega $ in 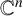${{\mathbb C}^n}$. In this paper, we establish a criterion for 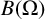$B(\Omega )$ to be reflexive via evaluation functions on 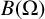$B(\Omega )$, that is, 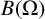$B(\Omega )$ is reflexive if and only if the evaluation functions span the dual space 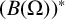$(B(\Omega ))^{*} $.

Keywords

Banach space of holomorphic functionsevaluation functionreflexivity

MSC classification

Primary: 32C37: Duality theorems 46A25: Reflexivity and semi-reflexivity 46E15: Banach spaces of continuous, differentiable or analytic functions
Secondary: 46A20: Duality theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , First View , pp. 1 - 14
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by NNSF of China (Grant Number 12071155). The second author was supported by NNSF of China (Grant Number 12371127). The third author is supported by the Australian Research Council (ARC) through the research grant DP220100285.

Communicated by Lisa Orloff Clark

References

Conway, J. B., A Course in Functional Analysis, Graduate Texts in Mathematics, 96 (Springer, New York, 1997).Google Scholar
Cowen, C. and MacCluer, B., Composition Operators on Spaces of Analytic Functions (CRC Press, Boca Raton, FL, 1995).Google Scholar
Hedenmalm, H., Kirenblum, B. and Zhu, K. H., Theory of Bergman Spaces, Graduate Texts in Mathematics, 199 (Springer, New York, 2000).CrossRefGoogle Scholar
Manhas, J. S. and Zhao, R., ‘Fredholm and frame-preserving weighted composition operators’, Complex Anal. Oper. Theory 18 (2024), 34.CrossRefGoogle Scholar
Ortega, J. M. and Fábrega, J., ‘Multipliers in Hardy–Sobolev spaces’, Integral Equations Operator Theory 55 (2006), 535–560.CrossRefGoogle Scholar
Rudin, W., Function Theory in the Unit Ball of ${\mathbb{C}}^n$ (Springer, New York, 1980).Google Scholar
Shields, A. L., ‘Weighted shift operators and analytic function theory’, Math. Surveys 13 (1974), 48–128.Google Scholar
Zhu, K. H., Operator Theory in Function Spaces (American Mathematical Society, Providence, RI, 2007).CrossRefGoogle Scholar