Hostname: page-component-f554764f5-sl7kg Total loading time: 0 Render date: 2025-04-11T18:12:19.629Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DISTRIBUTION OF THE NUMBER OF SUBGROUPS OF THE MULTIPLICATIVE GROUP

Part of: Multiplicative number theory

Published online by Cambridge University Press:  21 December 2018

GREG MARTIN  and
LEE TROUPE
GREG MARTIN
Affiliation:
Department of Mathematics, University of British Columbia, Room 121, 1984 Mathematics Road, Vancouver, BC, Canada V6T 1Z2 email [email protected]
LEE TROUPE*
Affiliation:
Department of Mathematics and Computer Science, University of Lethbridge, C526 University Hall, 4401 University Drive West, Lethbridge, AB, Canada T1K 3M4 email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 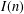$I(n)$ denote the number of isomorphism classes of subgroups of 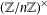$(\mathbb{Z}/n\mathbb{Z})^{\times }$, and let 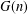$G(n)$ denote the number of subgroups of 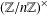$(\mathbb{Z}/n\mathbb{Z})^{\times }$ counted as sets (not up to isomorphism). We prove that both 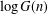$\log G(n)$ and 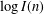$\log I(n)$ satisfy Erdős–Kac laws, in that suitable normalizations of them are normally distributed in the limit. Of note is that 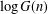$\log G(n)$ is not an additive function but is closely related to the sum of squares of additive functions. We also establish the orders of magnitude of the maximal orders of 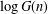$\log G(n)$ and 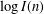$\log I(n)$.

Keywords

additive functionsdistribution of valuesmaximal ordermethod of momentscounting subgroups

MSC classification

Primary: 11N60: Distribution functions associated with additive and positive multiplicative functions 11N45: Asymptotic results on counting functions for algebraic and topological structures
Secondary: 11N37: Asymptotic results on arithmetic functions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 108 , Issue 1 , February 2020 , pp. 46 - 97
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Akbary, A. and Hambrook, K., ‘A variant of the Bombieri–Vinogradov theorem with explicit constants and applications’, Math. Comp. 84(294) (2015), 1901–1932.Google Scholar
Bessenrodt, C. and Ono, K., ‘Maximal multiplicative properties of partitions’, Ann. Comb. 20(1) (2016), 59–64.Google Scholar
Billingsley, P., Probability and Measure, 3rd edn, Wiley Series in Probability and Mathematical Statistics (A Wiley–Interscience Publication (John Wiley & Sons, Inc.), New York, 1995).Google Scholar
Erdős, P. and Kac, M., ‘The Gaussian law of errors in the theory of additive number theoretic functions’, Amer. J. Math. 62(1/4) (1940), 343–352.Google Scholar
Erdős, P. and Nicolas, J.-L., ‘Sur la fonction “nombre de facteurs premiers de n”’, Séminaire Delange–Pisot–Poitou. Théorie des nombres 20(2) (1978–1979), 1–19.Google Scholar
Erdős, P. and Pomerance, C., ‘The normal number of prime factors of 𝜑(n)’, Rocky Mountain. J. Math. 15 (1985), 343–352.Google Scholar
Friedlander, J. and Granville, A., ‘Limitations to the equi-distribution of primes. I’, Ann. of Math. (2) 129(2) (1989), 363–382.Google Scholar
Granville, A. and Soundararajan, K., ‘Sieving and the Erdős–Kac theorem’, in: Equidistribution in Number Theory, an Introduction, NATO Science Series, Series II: Mathematics, Physics and Chemistry, 237 (Springer, Dordrecht, 2007), 15–27.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society Colloquium Publications, 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Montgomery, H. L. and Vaughan, R. C., ‘Multiplicative number theory. I’, in: Classical Theory, Cambridge Studies in Advanced Mathematics, 97 (Cambridge University Press, Cambridge, 2007).Google Scholar
Norton, K. K., ‘On the number of restricted prime factors of an integer. I’, Illinois J. Math. 20(4) (1976), 681–705.Google Scholar
Pomerance, C., ‘On the distribution of amicable numbers’, J. reine angew. Math. 293/294 (1977), 217–222.Google Scholar
Stehling, T., ‘On computing the number of subgroups of a finite abelian group’, Combinatorica 12(4) (1992), 475–479.Google Scholar
Xylouris, T., Über die Nullstellen der Dirichletschen L-Funktionen und die kleinste Primzahl in einer arithmetischen Progression, Bonner Mathematische Schriften [Bonn Mathematical Publications], 404 (Universität Bonn, Mathematisches Institut, Bonn, 2011), Dissertation for the degree of Doctor of Mathematics and Natural Sciences at the University of Bonn, Bonn, 2011.Google Scholar