Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T13:37:49.734Z Has data issue: false hasContentIssue false
  • English
  • Français

The diameter of an immersed Riemannian manifold with bounded mean curvature

Part of: Global differential geometry

Published online by Cambridge University Press:  09 April 2009

Th. Koufogiorgos  and
Ch. Baikoussis
Th. Koufogiorgos
Affiliation:
Department of Mathematics, University of Ioannina, Ioannina, Greece
Ch. Baikoussis
Affiliation:
Department of Mathematics, University of Ioannina, Ioannina, Greece
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M be an n-dimensional complete Riemannian manifold with Ricci curvature bounded from below. Let 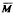be an N-dimensional (N < n) complete, simply connected Riemannian manifold with nonpositive sectional curvature. We shall prove in this note that if there exists an isometric immersion φ of M into 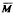with the property that the immersed manifold is contained in a ball of radius R and that the mean curvature vector H of the immersion has bounded norm ∥H∥ > H0, (H0 > 0) then R > H−10.

MSC classification

Secondary: 53C40: Global submanifolds
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 31 , Issue 2 , August 1981 , pp. 189 - 192
Copyright
Copyright © Australian Mathematical Society 1982

References

Aminov, J. (1973), ‘The exterior diameter of an immersed Riemannian manifold’, Math. USSR-Sb. 21, 449–454 (AMS translation).CrossRefGoogle Scholar
Hasanis, Th. and Koutroufiotis, D. (1979), ‘Immersions of bounded mean curvature’, Arc. Math. (Basel) 33, 170–171.CrossRefGoogle Scholar
Omori, H. (1967), ‘Isometric immersions of Riemannian manifold’, J. Math. Soc. Japan 19, 205–214.CrossRefGoogle Scholar