Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T13:42:55.615Z Has data issue: false hasContentIssue false
  • English
  • Français

CHEBYSHEV SUBSETS OF A HILBERT SPACE SPHERE

Part of: Approximations and expansions Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  21 November 2019

THEO BENDIT
THEO BENDIT*
Affiliation:
University of Newcastle, Australia email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Chebyshev conjecture posits that Chebyshev subsets of a real Hilbert space 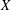$X$ are convex. Works by Asplund, Ficken and Klee have uncovered an equivalent formulation of the Chebyshev conjecture in terms of uniquely remotal subsets of 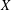$X$. In this tradition, we develop another equivalent formulation in terms of Chebyshev subsets of the unit sphere of 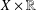$X\times \mathbb{R}$. We characterise such sets in terms of the image under stereographic projection. Such sets have superior structure to Chebyshev sets and uniquely remotal sets.

Keywords

Chebyshev setsChebyshev conjecturestereographic projectionproximal pointsfurthest points

MSC classification

Primary: 41A65: Abstract approximation theory (approximation in normed linear spaces and other abstract spaces)
Secondary: 41A50: Best approximation, Chebyshev systems 46B20: Geometry and structure of normed linear spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 107 , Issue 3 , December 2019 , pp. 289 - 301
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Asplund, E., ‘Čebyšev sets in Hilbert space’, Trans. Amer. Math. Soc. 144 (1969), 235–240.Google Scholar
Balaganskiĭ, V. S. and Vlasov, L. P., ‘The problem of the convexity of Chebyshev sets’, Uspekhi Mat. Nauk 51(6(312)) (1996), 125–188.Google Scholar
Bunt, L., ‘Bijdrage tot de theorie der konvekse puntverzamelingen’, PhD Thesis, University of Groningen, Amsterdam, 1934.Google Scholar
Efimov, N. V. and Stečkin, S. V., ‘Čebyšev sets in Banach spaces’, Dokl. Akad. Nauk SSSR 121 (1958), 582–585.Google Scholar
Fletcher, J. and Moors, W. B., ‘Chebyshev sets’, J. Aust. Math. Soc. 98(2) (2015), 161–231.Google Scholar
Johnson, G. G., ‘A nonconvex set which has the unique nearest point property’, J. Approx. Theory 51(4) (1987), 289–332.Google Scholar
Kelly, B. F., ‘The convexity of Chebyshev sets in finite dimensional normed linear spaces’, Master’s Thesis, The Pennsylvania State University, 1978.Google Scholar
Klee, V., ‘Convexity of Chebyshev sets’, Math. Ann. 142(6) (1961), 292–304.Google Scholar
Kritikos, N., ‘Sur quelques propriétés des ensembles convexes’, Bull. Math. Soc. Sci. Math. Roumanie 40(1–2) (1938), 87–92.Google Scholar
Motzkin, T. S., ‘Sur quelques propriétés caractéristiques des ensembles bornés non convexes’, Rend. Acad. dei Lincei (Roma) 21(6) (1935), 773–779.Google Scholar